 Метод узлов в заданиях В 3
Метод узлов в заданиях В 3
 Узел координатной сетки – это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки. Здесь узлы не обозначены.
Узел координатной сетки – это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки. Здесь узлы не обозначены.
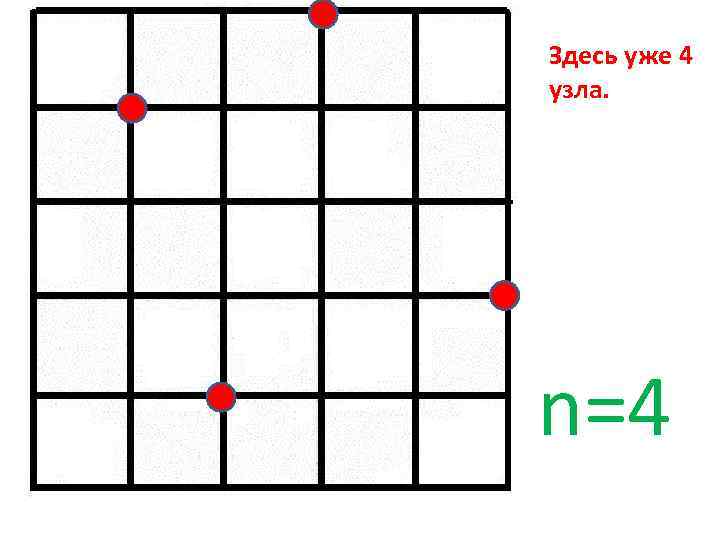 Здесь уже 4 узла. n=4
Здесь уже 4 узла. n=4
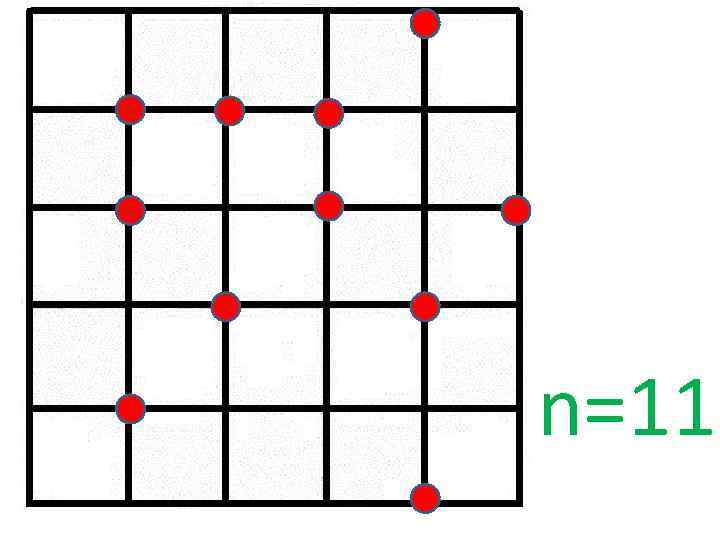 n=11
n=11
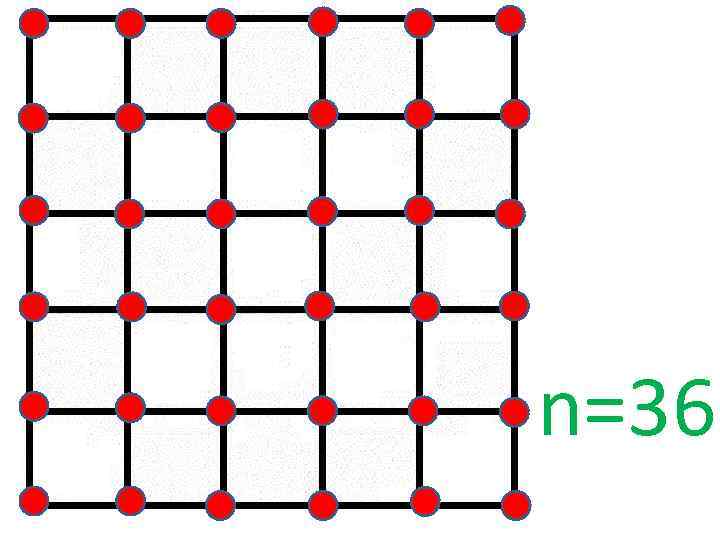 n=36
n=36
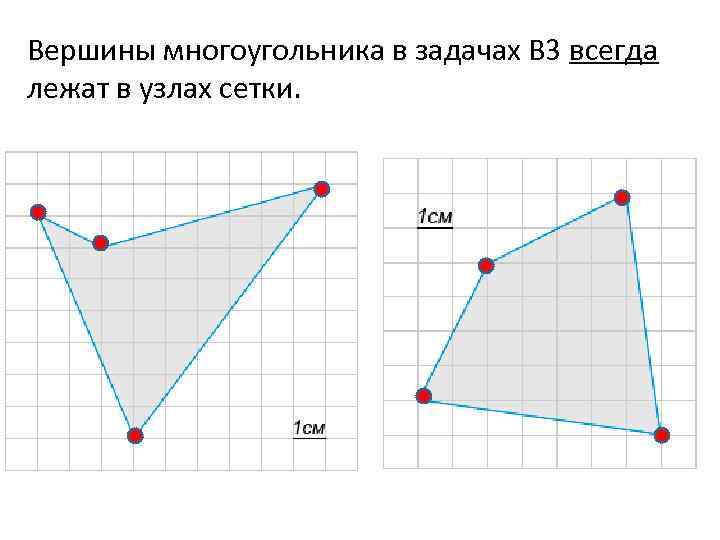 Вершины многоугольника в задачах В 3 всегда лежат в узлах сетки.
Вершины многоугольника в задачах В 3 всегда лежат в узлах сетки.
 И для них работает следующая теорема: Теорема: Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки, тогда площадь многоугольника будет равна: Где n – число узлов k -1 S=n+ 2 внутри многоугольника k – число узлов, лежащие на границе многоугольника.
И для них работает следующая теорема: Теорема: Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки, тогда площадь многоугольника будет равна: Где n – число узлов k -1 S=n+ 2 внутри многоугольника k – число узлов, лежащие на границе многоугольника.
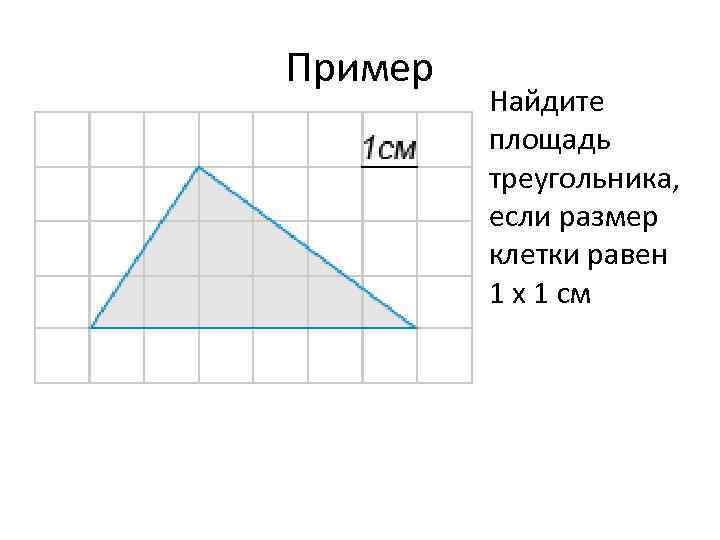 Пример Найдите площадь треугольника, если размер клетки равен 1 x 1 см
Пример Найдите площадь треугольника, если размер клетки равен 1 x 1 см
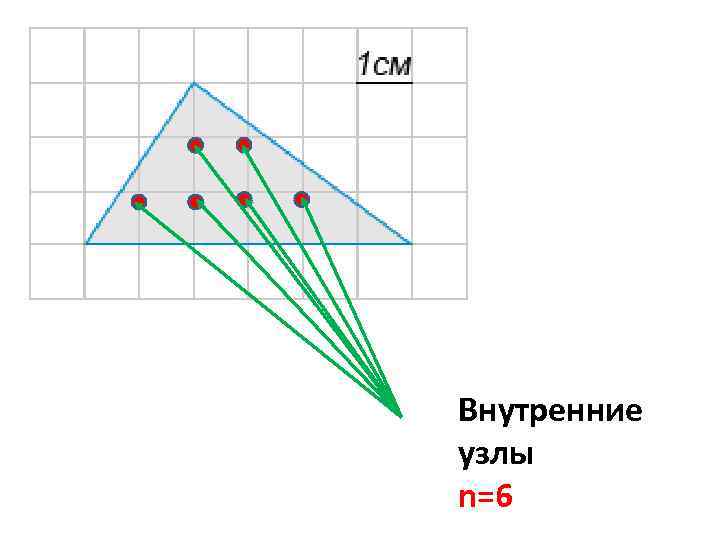 Внутренние узлы n=6
Внутренние узлы n=6
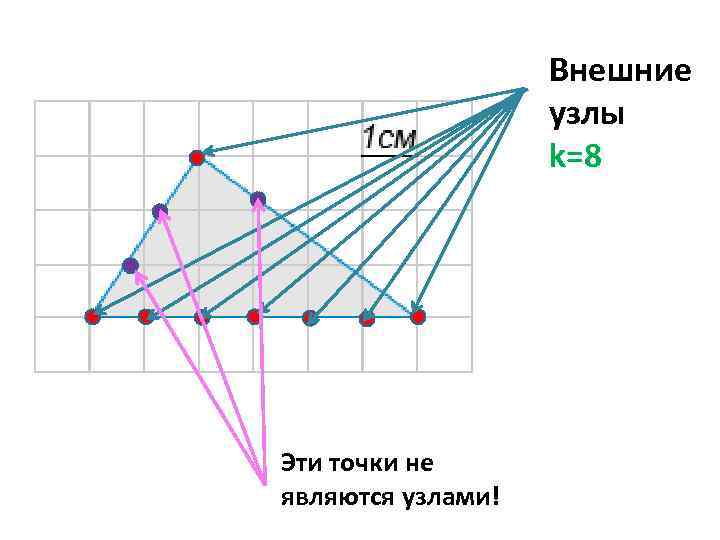 Внешние узлы k=8 Эти точки не являются узлами!
Внешние узлы k=8 Эти точки не являются узлами!
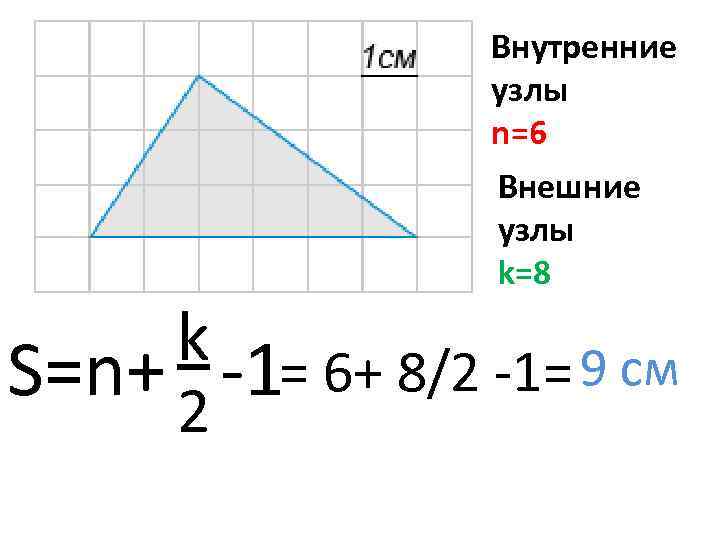 Внутренние узлы n=6 Внешние узлы k=8 k -1= 6+ 8/2 -1= 9 см S=n+ 2
Внутренние узлы n=6 Внешние узлы k=8 k -1= 6+ 8/2 -1= 9 см S=n+ 2
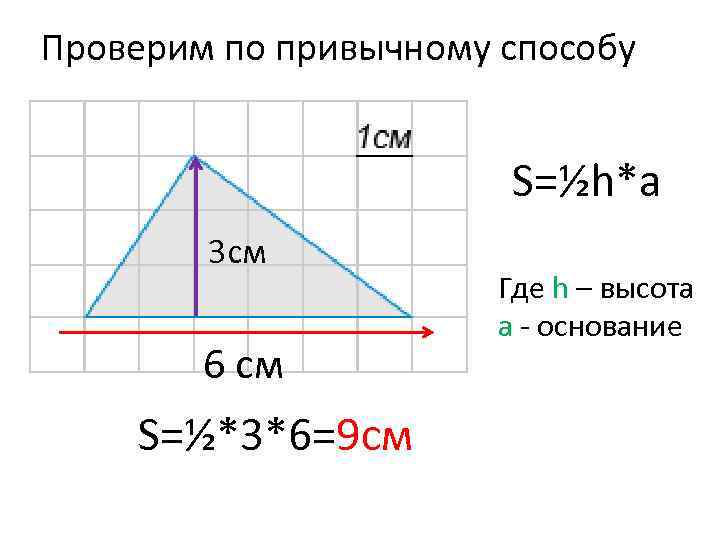 Проверим по привычному способу S=½h*a 3 см 6 см S=½*3*6=9 см Где h – высота a - основание
Проверим по привычному способу S=½h*a 3 см 6 см S=½*3*6=9 см Где h – высота a - основание
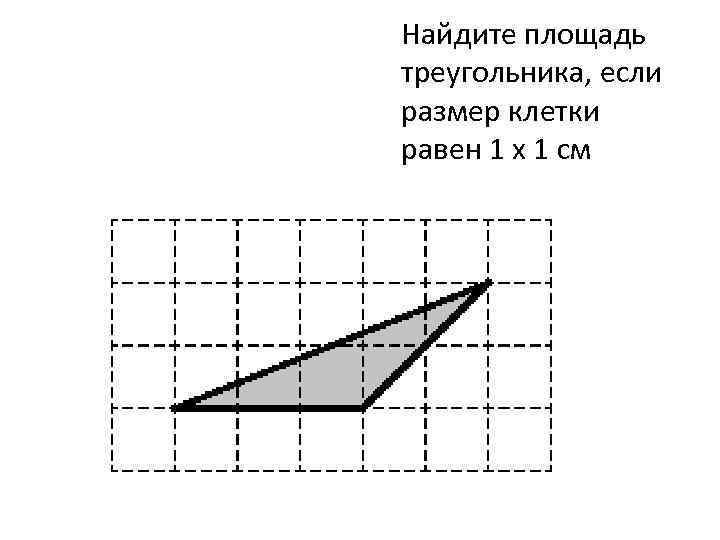 Найдите площадь треугольника, если размер клетки равен 1 x 1 см
Найдите площадь треугольника, если размер клетки равен 1 x 1 см
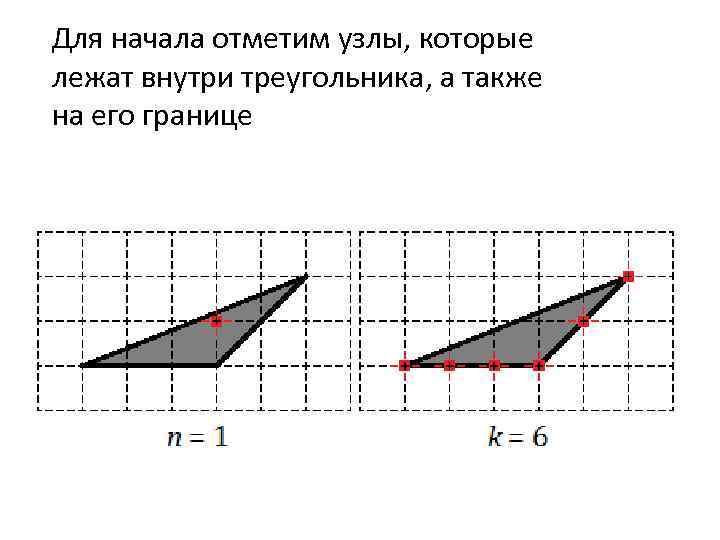 Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе
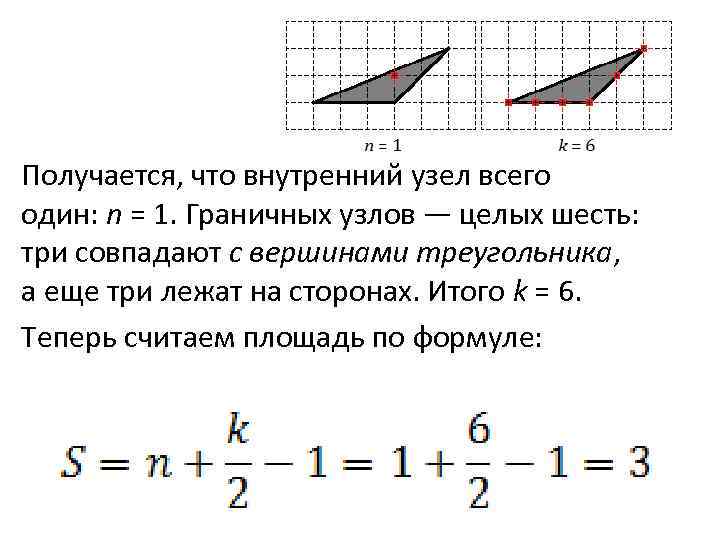 Получается, что внутренний узел всего один: n = 1. Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах. Итого k = 6. Теперь считаем площадь по формуле:
Получается, что внутренний узел всего один: n = 1. Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах. Итого k = 6. Теперь считаем площадь по формуле:
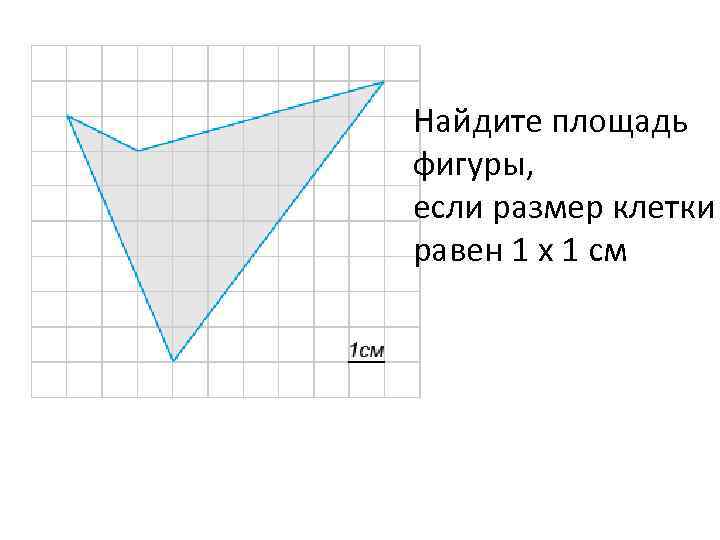 Найдите площадь фигуры, если размер клетки равен 1 x 1 см
Найдите площадь фигуры, если размер клетки равен 1 x 1 см
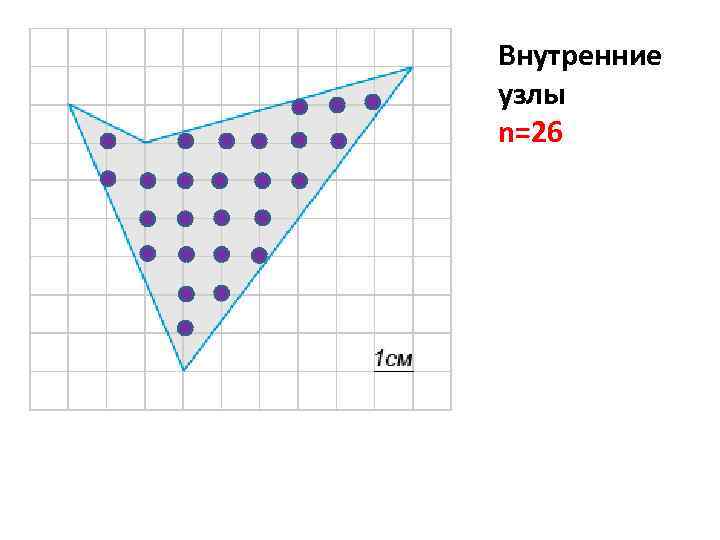 Внутренние узлы n=26
Внутренние узлы n=26
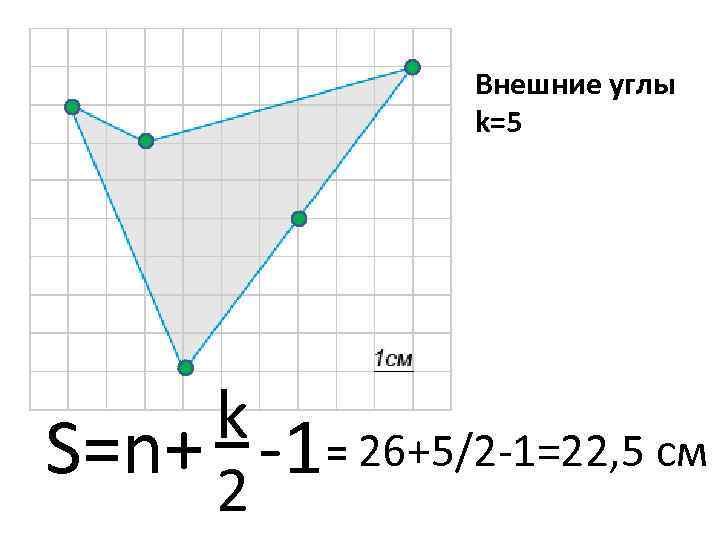 Внешние углы k=5 k -1 = 26+5/2 -1=22, 5 см S=n+ 2
Внешние углы k=5 k -1 = 26+5/2 -1=22, 5 см S=n+ 2
 Важное замечание Но формула – это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Важное замечание Но формула – это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
 Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт: Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых» : 10, 5; 17, 5 и т. д.
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт: Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых» : 10, 5; 17, 5 и т. д.