Метод сеток при решении дифференциальных уравнений с частными

Метод сеток при решении дифференциальных уравнений с частными производными

Постановка задачи Опр. 1. Дифференциальным уравнением в частных производных называется равенство, содержащее неизвестную функцию от нескольких переменных, независимые переменные и частные производные по независимым переменным

Типы однородных уравнений с постоянными коэффициентами Гиперболического типа: волновое уравнение Эллиптического типа: уравнение Лапласа Параболического типа: уравнение Фурье

Точные методы решения таких уравнений не всегда приемлемы. В связи с этим разработаны приближенные методы решения таких уравнений. Наиболее распространенными являются сеточные методы. При решении задач сеточными методами мы получаем совокупность приближенных значений решения в некоторой конечной системе точек. В случае необходимости можно построить формулу (например, интерполяционную) для приближенного представления решения во всей области

Приближенное решение уравнения Лапласа Метод сеток

Пусть дано уравнение Лапласа Найти приближенное решение этого уравнения в квадрате АВСD, где А(0, 0); В(0, 1); С(1, 1); D(1, 0) с точностью ε = 0, 01 и шагом h = 0, 2, Если на сторонах квадрата функция задана следующими начальными условиями:

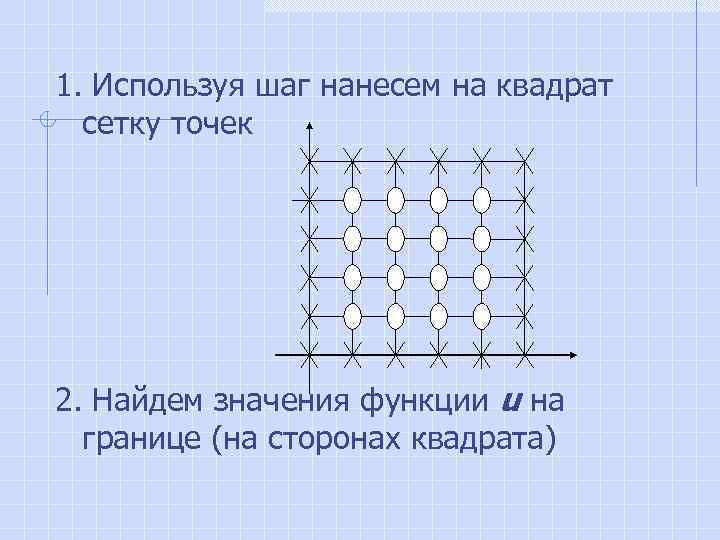1. Используя шаг нанесем на квадрат сетку точек 2. Найдем значения функции u на границе (на сторонах квадрата)

На стороне АВ функция удовлетворяет условию (1), следовательно подставим координаты точек, находящихся на стороне АВ в это равенство, получим: u(0, 0) = 1, 5; u(0; 0, 2) = 1, 491; u(0; 0, 4) = 1, 522; u(0; 0, 6) = 1, 593; u(0; 0, 8) = 1, 704; u(0, 1) = 1, 855

На стороне BC функция удовлетворяет условию (2), следовательно подставим координаты точек, находящихся на стороне ВC в это равенство, получим: u(0, 1) = 1, 855; u(0, 2; 1) = 1, 269; u(0, 4; 1) = 1, 013; u(0, 6; 1) = 0, 815; u(0, 8; 1) = 0, 647; u(1, 1) = 0, 5

На стороне CD функция удовлетворяет условию (3), следовательно подставим координаты точек, находящихся на стороне CD в это равенство, получим: u(1, 1) = 0, 5; u(1; 0, 8) = 0, 8; u(1; 0, 6) = 1, 1; u(1; 0, 4) = 1, 4; u(1; 0, 2) = 1, 7; u(1, 0) = 2

На стороне AD функция удовлетворяет условию (4), следовательно подставим координаты точек, находящихся на стороне AD в это равенство, получим: u(1, 0) = 2; u(0, 8; 0) = 1, 975; u(0, 6; 0) = 1, 904; u(0, 4; 0) = 1, 793; u(0, 2; 0) = 1, 654; u(0, 0) = 1, 5

3. По результатам вычислений заполняем шаблон Шаблон № 0 1 1, 866 1, 268 1, 013 0, 815 0, 647 0, 5 0, 8 1, 704 0, 8 0, 6 1, 593 1, 1 0, 4 1, 522 1, 4 0, 2 1, 491 1, 7 0 1, 5 1, 654 1, 793 1, 904 1, 975 2 0 0, 2 0, 4 0, 6 0, 8 1

4. Вычислим значения функции во внутренних точках сетки. Во внутренние клетки шаблона № 0 можно проставлять любые значения, например равномерно распределенные по горизонтали

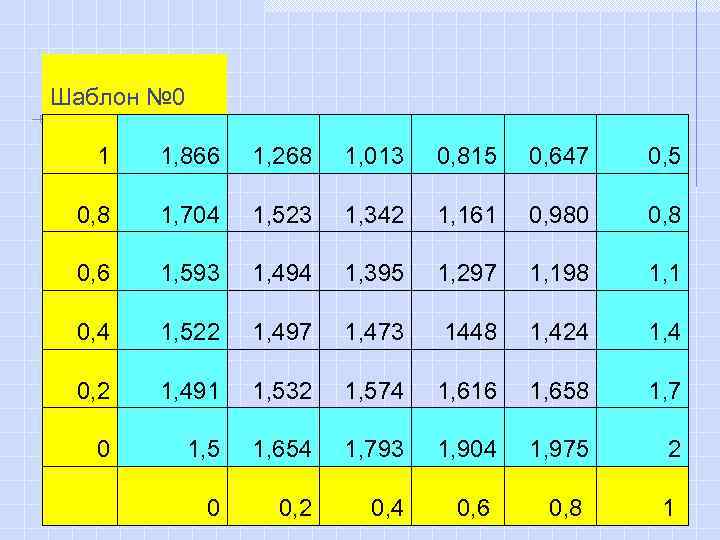Шаблон № 0 1 1, 866 1, 268 1, 013 0, 815 0, 647 0, 5 0, 8 1, 704 1, 523 1, 342 1, 161 0, 980 0, 8 0, 6 1, 593 1, 494 1, 395 1, 297 1, 198 1, 1 0, 4 1, 522 1, 497 1, 473 1448 1, 424 1, 4 0, 2 1, 491 1, 532 1, 574 1, 616 1, 658 1, 7 0 1, 5 1, 654 1, 793 1, 904 1, 975 2 0 0, 2 0, 4 0, 6 0, 8 1

Шаблон № 0 представляет из себя приближенное решение (нулевое приближение) уравнения Лапласа. 5. Для уточнения решения составляют шаблон № 1.

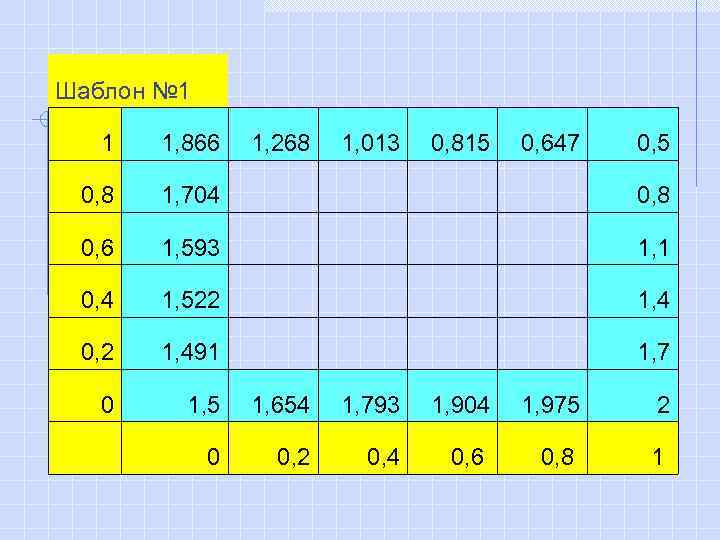Шаблон № 1 1 1, 866 1, 268 1, 013 0, 815 0, 647 0, 5 0, 8 1, 704 0, 8 0, 6 1, 593 1, 1 0, 4 1, 522 1, 4 0, 2 1, 491 1, 7 0 1, 5 1, 654 1, 793 1, 904 1, 975 2 0 0, 2 0, 4 0, 6 0, 8 1

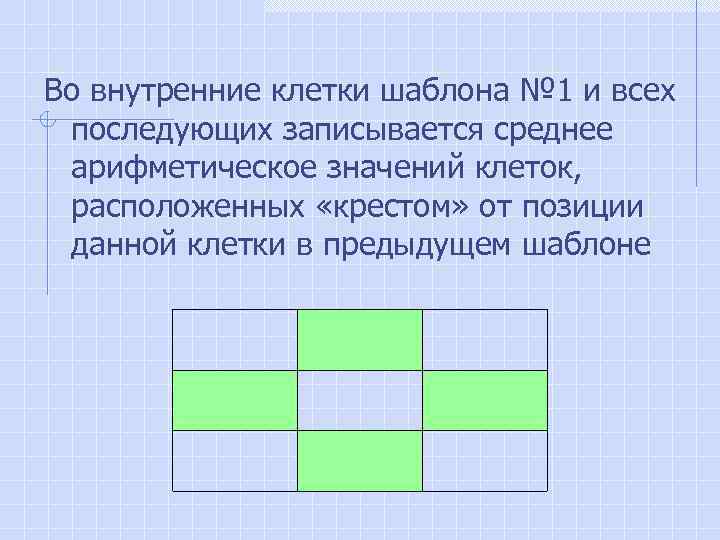Во внутренние клетки шаблона № 1 и всех последующих записывается среднее арифметическое значений клеток, расположенных «крестом» от позиции данной клетки в предыдущем шаблоне

Процесс уточнения решений дифференциального уравнения продолжается до тех пор, пока все разности значений последнего полученного шаблона и соответствующих им значений предыдущего шаблона по абсолютной величие не будут меньше заданной точности (0, 001).