08_Integr.ppt
- Количество слайдов: 24
 Метод прямоугольников -интегрирование слева -интегрирование справа -интегрирование по центру Метод трапеций Метод Симпсона Формула Ньютона-Котеса 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Метод прямоугольников -интегрирование слева -интегрирование справа -интегрирование по центру Метод трапеций Метод Симпсона Формула Ньютона-Котеса 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
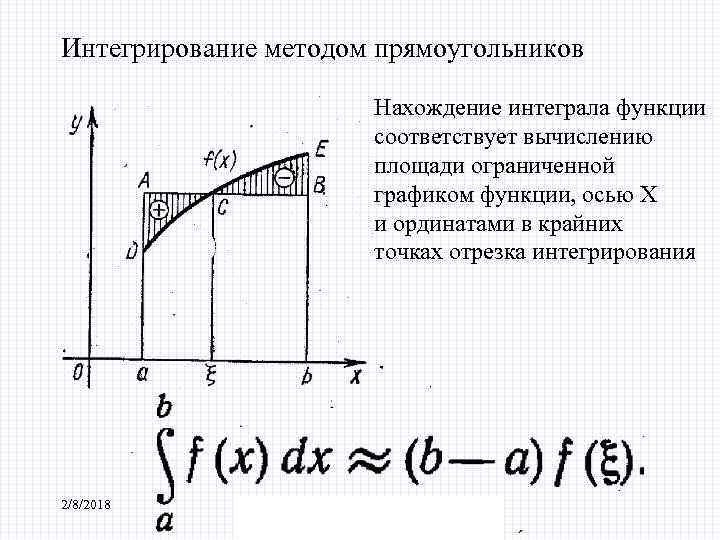 Интегрирование методом прямоугольников Нахождение интеграла функции соответствует вычислению площади ограниченной графиком функции, осью Х и ординатами в крайних точках отрезка интегрирования 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Интегрирование методом прямоугольников Нахождение интеграла функции соответствует вычислению площади ограниченной графиком функции, осью Х и ординатами в крайних точках отрезка интегрирования 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
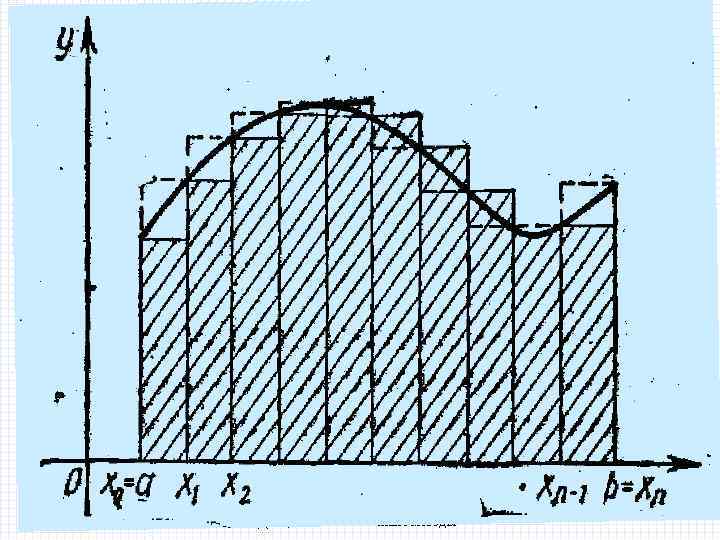 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
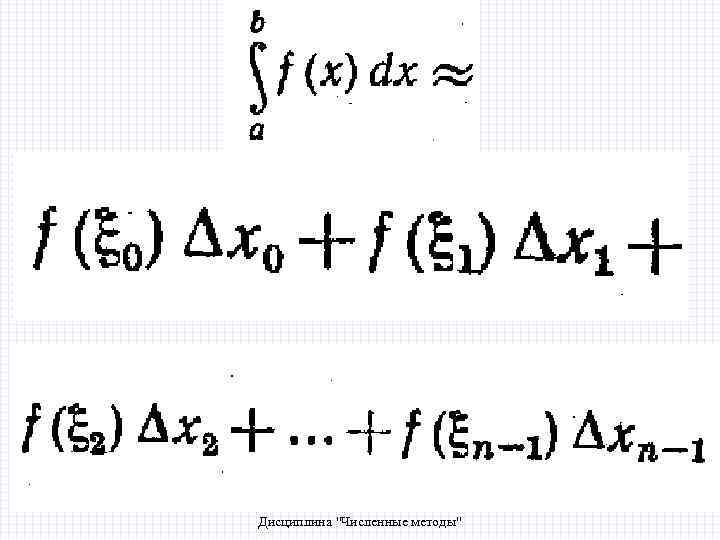 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
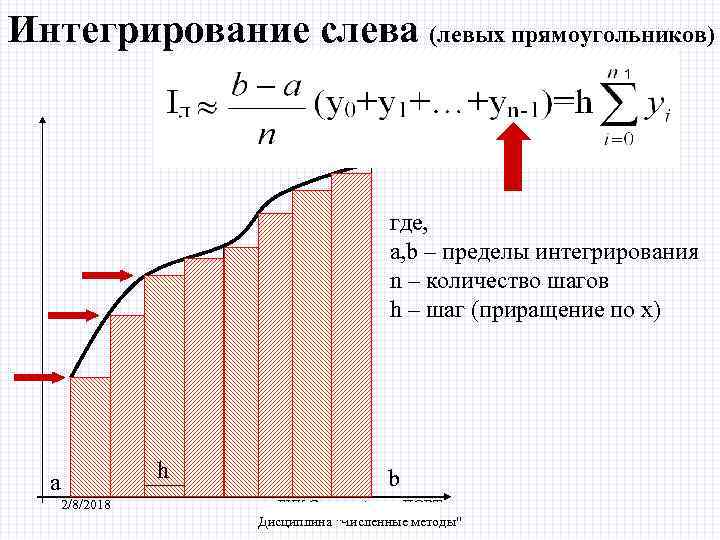 Интегрирование слева (левых прямоугольников) где, a, b – пределы интегрирования n – количество шагов h – шаг (приращение по х) h a 2/8/2018 b b БИК Специальность ПОВТ Дисциплина "Численные методы"
Интегрирование слева (левых прямоугольников) где, a, b – пределы интегрирования n – количество шагов h – шаг (приращение по х) h a 2/8/2018 b b БИК Специальность ПОВТ Дисциплина "Численные методы"
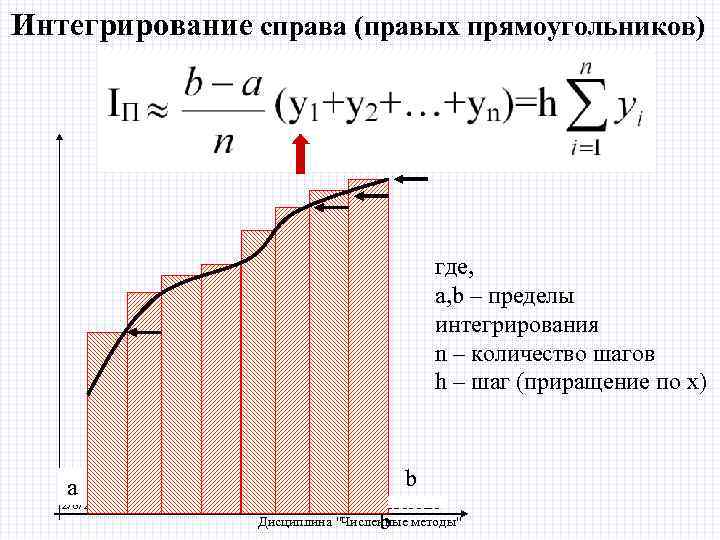 Интегрирование справа (правых прямоугольников) где, a, b – пределы интегрирования n – количество шагов h – шаг (приращение по х) a 2/8/2018 b БИК Специальность ПОВТ Дисциплина "Численные методы" b
Интегрирование справа (правых прямоугольников) где, a, b – пределы интегрирования n – количество шагов h – шаг (приращение по х) a 2/8/2018 b БИК Специальность ПОВТ Дисциплина "Численные методы" b
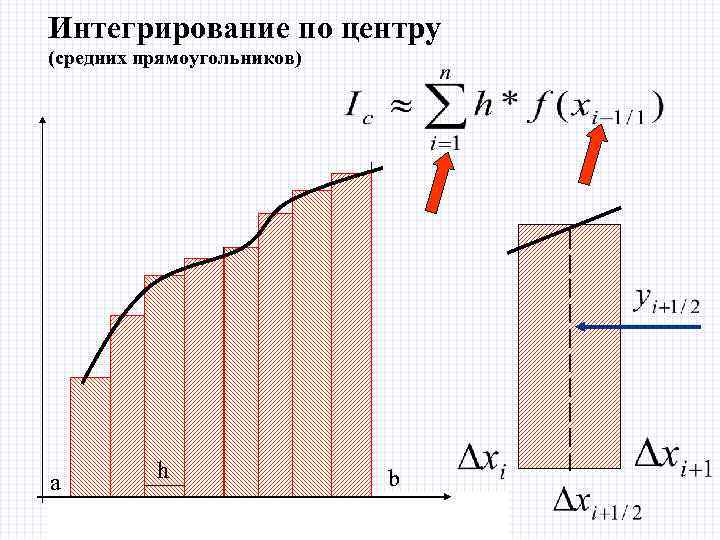 Интегрирование по центру (средних прямоугольников) h a 2/8/2018 b БИК Специальность ПОВТ Дисциплина "Численные методы"
Интегрирование по центру (средних прямоугольников) h a 2/8/2018 b БИК Специальность ПОВТ Дисциплина "Численные методы"
 Пример 1. С помощью формул левых и правых прямоугольников вычислить , полагая n=4 Решение 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Пример 1. С помощью формул левых и правых прямоугольников вычислить , полагая n=4 Решение 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
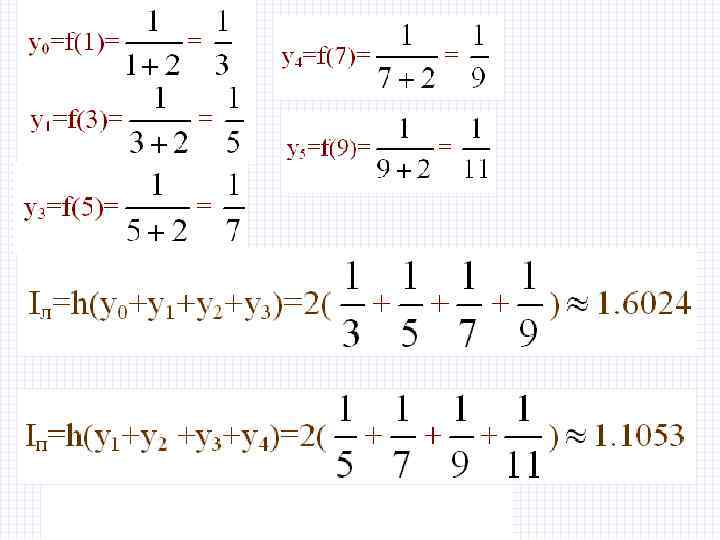 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 Расчет для центральных прямоугольников Сравнение результатов 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" Конец раздела
Расчет для центральных прямоугольников Сравнение результатов 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" Конец раздела
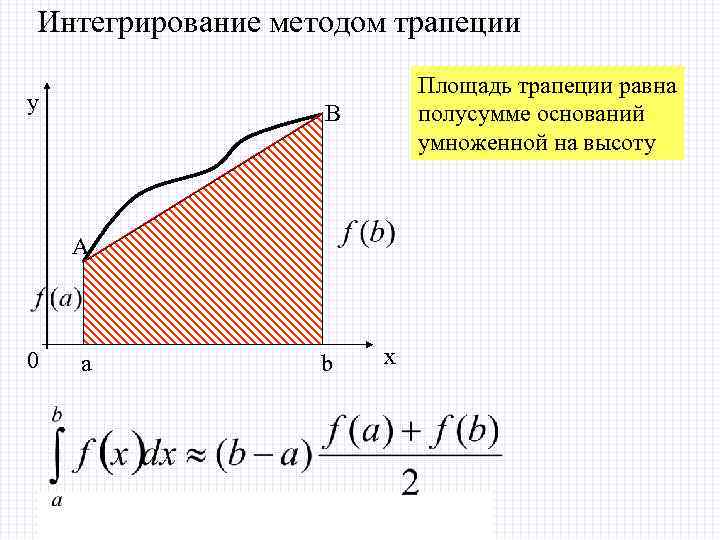 Интегрирование методом трапеции y Площадь трапеции равна полусумме оснований умноженной на высоту B А 0 a 2/8/2018 b x БИК Специальность ПОВТ Дисциплина "Численные методы"
Интегрирование методом трапеции y Площадь трапеции равна полусумме оснований умноженной на высоту B А 0 a 2/8/2018 b x БИК Специальность ПОВТ Дисциплина "Численные методы"
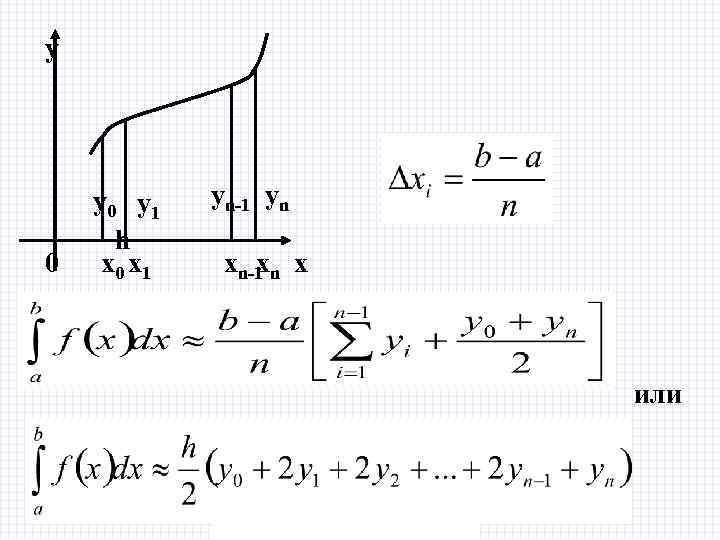 y 0 y 1 h x 0 x 1 yn-1 yn xn-1 n х x или 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
y 0 y 1 h x 0 x 1 yn-1 yn xn-1 n х x или 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 Пример. Пользуясь общей трапеций, вычислить формулой при n=4 Решение h=(1 -0)/4=1/4=0. 25 x 0=0 x 1=0. 25 x 2=0. 5 x 3=0. 75 x 4=1 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Пример. Пользуясь общей трапеций, вычислить формулой при n=4 Решение h=(1 -0)/4=1/4=0. 25 x 0=0 x 1=0. 25 x 2=0. 5 x 3=0. 75 x 4=1 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 y(x 0)= y(0)=1/(1+0)=1 y(x 1)= y(0. 25)=1/(1+0. 0625)= y(x 2)= y(0. 5)=1/(1+0. 25)= y(x 3)= y(0. 75)=1/(1+0. 5625)= y(x 4)= y(1)=1/(1+1)= 0. 5 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
y(x 0)= y(0)=1/(1+0)=1 y(x 1)= y(0. 25)=1/(1+0. 0625)= y(x 2)= y(0. 5)=1/(1+0. 25)= y(x 3)= y(0. 75)=1/(1+0. 5625)= y(x 4)= y(1)=1/(1+1)= 0. 5 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 Расчетное значение = 0, 785 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" Конец раздела
Расчетное значение = 0, 785 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" Конец раздела
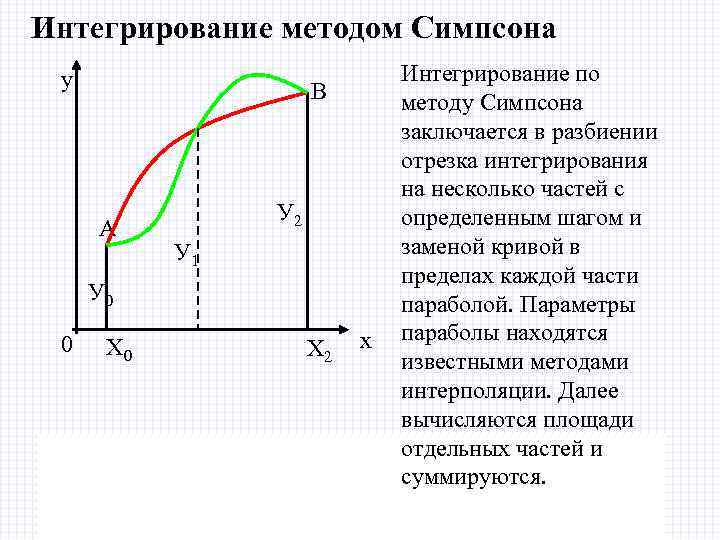 Интегрирование методом Симпсона y B А У 2 У 1 У 0 0 Х 0 2/8/2018 Х 2 Х 1 x Интегрирование по методу Симпсона заключается в разбиении отрезка интегрирования на несколько частей с определенным шагом и заменой кривой в пределах каждой части параболой. Параметры параболы находятся известными методами интерполяции. Далее вычисляются площади отдельных частей и суммируются. БИК Специальность ПОВТ Дисциплина "Численные методы"
Интегрирование методом Симпсона y B А У 2 У 1 У 0 0 Х 0 2/8/2018 Х 2 Х 1 x Интегрирование по методу Симпсона заключается в разбиении отрезка интегрирования на несколько частей с определенным шагом и заменой кривой в пределах каждой части параболой. Параметры параболы находятся известными методами интерполяции. Далее вычисляются площади отдельных частей и суммируются. БИК Специальность ПОВТ Дисциплина "Численные методы"
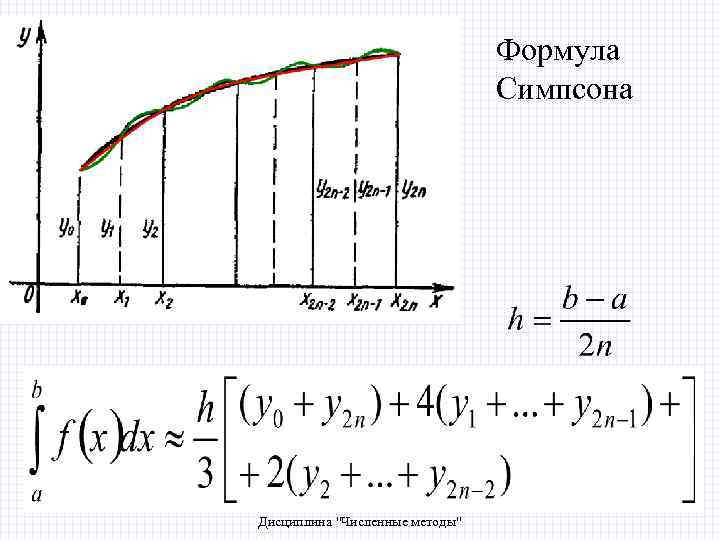 Формула Симпсона 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Формула Симпсона 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 Пример. Пользуясь формулой Симпсона, вычислить при h=0, 25 Решение x 0=0 x 1=0. 25 x 2=0. 5 x 3=0. 75 x 4=1 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Пример. Пользуясь формулой Симпсона, вычислить при h=0, 25 Решение x 0=0 x 1=0. 25 x 2=0. 5 x 3=0. 75 x 4=1 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 y(x 0)= y(0)=1/(1+0)=1 y(x 1)= y(0. 25)=1/(1+0. 0625)=1/1, 0625 y(x 2)= y(0. 5)=1/(1+0. 25)=1/1, 25 y(x 3)= y(0. 75)=1/(1+0. 5625)=1/1, 5625 y(x 4)= y(1)=1/(1+1)= 1/2 Метод трапеций = 0, 7854, расчетное значение = 0, 785 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" Конец раздела
y(x 0)= y(0)=1/(1+0)=1 y(x 1)= y(0. 25)=1/(1+0. 0625)=1/1, 0625 y(x 2)= y(0. 5)=1/(1+0. 25)=1/1, 25 y(x 3)= y(0. 75)=1/(1+0. 5625)=1/1, 5625 y(x 4)= y(1)=1/(1+1)= 1/2 Метод трапеций = 0, 7854, расчетное значение = 0, 785 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" Конец раздела
 Обобщенная формула Ньютона-Котеса Коэфф. Ньютона-Котеса 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Обобщенная формула Ньютона-Котеса Коэфф. Ньютона-Котеса 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 Пример2. Вычислить по формуле Ньютона-Котеса , выбрав n=4 Решение 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
Пример2. Вычислить по формуле Ньютона-Котеса , выбрав n=4 Решение 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
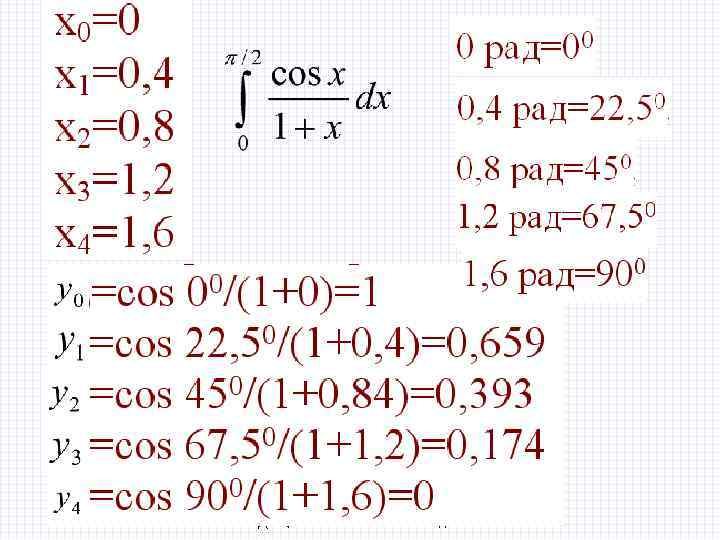 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы"
 Расчетное значение = 0, 674 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" The end….
Расчетное значение = 0, 674 2/8/2018 БИК Специальность ПОВТ Дисциплина "Численные методы" The end….


