МЕТОД ПРЕЛОМЛЕННЫХ ВОЛН ГОЛОВНЫЕ ВОЛНЫ СЕЙСМОРАЗВЕДКА НА ПРЕЛОМЛЕННЫХ

МЕТОД ПРЕЛОМЛЕННЫХ ВОЛН. ГОЛОВНЫЕ ВОЛНЫ. СЕЙСМОРАЗВЕДКА НА ПРЕЛОМЛЕННЫХ (ГОЛОВНЫХ) ВОЛНАХ

МЕТОД ПРЕЛОМЛЕННЫХ ВОЛН • Годограф отраженных волн не содержит информации о скорости волн в породах, залегающих ниже отражающей границы. Преломленные волны, проходящие часть своего пути вдоль преломляющей границы со скоростью волн в подстилающей толще, восполняют этот недостаток отраженных волн. Кроме того, при исследовании малых глубин отраженные волны интерферируют с больших количеством других волн, которые являются помехами для МОВ. Поэтому на помощь приходит Метод Преломленных Волн. Отраженные и преломленные волны при совместном использовании в ряде случаев значительно расширяют возможности сейсморазведки

Условие образования головных волн • Если в изучаемой толще имеются границы, на которых скорость волн скачкообразно возрастает, превышая каждое из предшествующих значений, то на таких границах будут образовываться преломленные волны, несущие информацию о скоростях в породах, подстилающих соответствующую границу. • Для образования головной волны на 1 -ой границе надо, чтобы с1

Условие образования головных волн Покажем, что для образования головной волны на 2 -ой границе требуется, чтобы с2

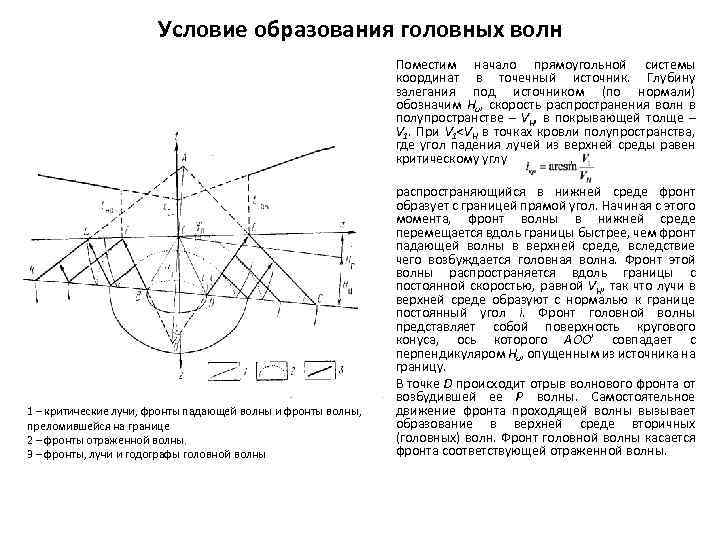Условие образования головных волн Поместим начало прямоугольной системы координат в точечный источник. Глубину залегания под источником (по нормали) обозначим Hи, скорость распространения волн в полупространстве – VH, в покрывающей толще – V 1. При V 1

Условие образования головных волн • Для образования головной волны обязательно должна быть небольшая кривизна волнового фронта. Иначе образование головной волны невозможно. Для их образования достаточно даже остаточной кривизны фронта на больших расстояниях от источника – примером чего являются исследования Русской платформы. • Волна, распространяющаяся вдоль границы, может порождать S-волны в первой среде. При этом угол выхода будет выражаться следующей формулой

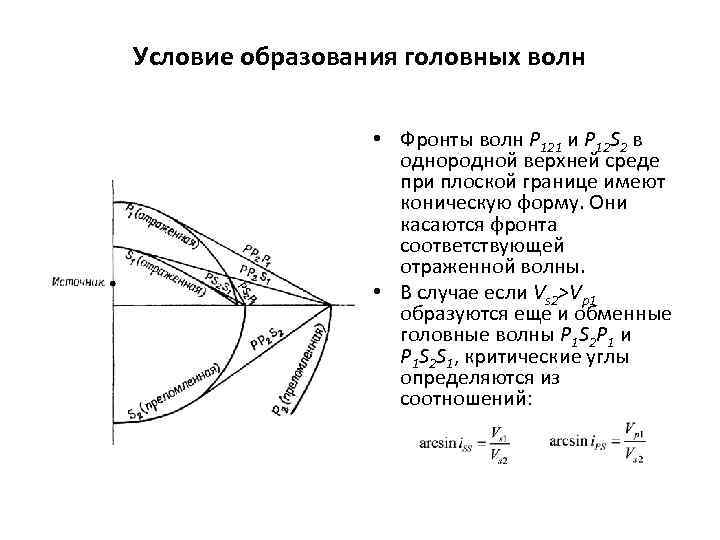Условие образования головных волн • Фронты волн P 121 и P 12 S 2 в однородной верхней среде при плоской границе имеют коническую форму. Они касаются фронта соответствующей отраженной волны. • В случае если Vs 2>Vp 1 образуются еще и обменные головные волны P 1 S 2 P 1 и P 1 S 2 S 1, критические углы определяются из соотношений:

Условие образования головных волн • Форма импульса головной волны существенно отличается от формы импульса падающей. На больших расстояниях между источником и приемником импульс смещения головной волны связан с импульсом падающей волны как где f(t) - импульс падающей волны. • Различные виды головных волн могли бы представлять интерес в сейсморазведке, т. к. они несут информацию о подстилающей границу толще, но из-за неоднородности среды возникают более интенсивные рефрагированные волны, причем они распространяются в направлении, близком к направлению границы. На практике наиболее часто имеют дело с P 1 P 2 P 1.

Условие образования головных волн • Обнаружение головной волны по кинематическим признакам должно основываться на критериях отсутствия систематического изменения кажущейся скорости с расстоянием и постоянства разности времен нагоняющего и нагоняемого годографов на участках с плоской формой границы. Однако из-за влияния помех всегда допустимо предполагать, что t и V* в действительности непостоянны, но величина их изменения лежит в пределах точности измерений. Одних кинематических критериев недостаточно для обнаружения головной волны. Из динамических критериев эффективен признак изменения формы импульса головной волны по сравнению с формой колебания падающей.

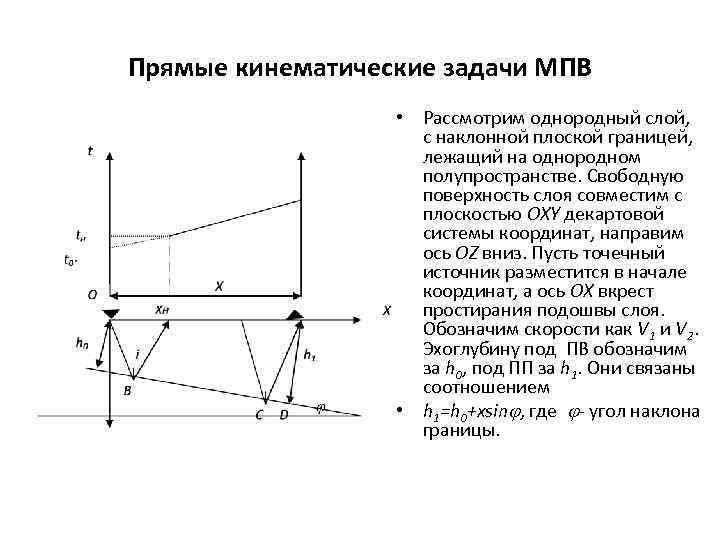Прямые кинематические задачи МПВ • Рассмотрим однородный слой, с наклонной плоской границей, лежащий на однородном полупространстве. Свободную поверхность слоя совместим с плоскостью OXY декартовой системы координат, направим ось OZ вниз. Пусть точечный источник разместится в начале координат, а ось OX вкрест простирания подошвы слоя. Обозначим скорости как V 1 и V 2. Эхоглубину под ПВ обозначим за h 0, под ПП за h 1. Они связаны соотношением • h 1=h 0+xsin , где - угол наклона границы.

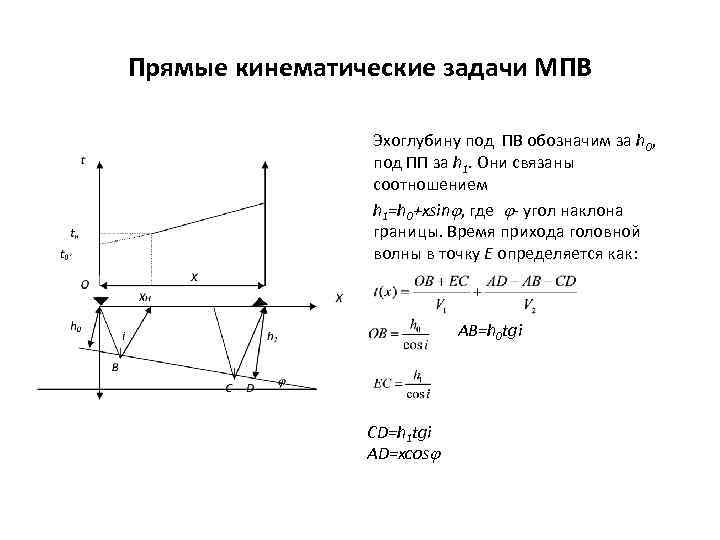Прямые кинематические задачи МПВ Эхоглубину под ПВ обозначим за h 0, под ПП за h 1. Они связаны соотношением h 1=h 0+xsin , где - угол наклона границы. Время прихода головной волны в точку E определяется как: АВ=h 0 tgi CD=h 1 tgi AD=xcos

Прямые кинематические задачи МПВ Имеем Поскольку

Прямые кинематические задачи МПВ Знак «+» берется в случае падения границы в сторону от источника к приемнику. При падении границы в сторону от приемника к источнику, берется знак «-» , h 1=h 0 -xsin и Эти формулы можно объединить в одну Таким образом, годограф головной волны для наклонной плоской границы в прямоугольных координатах (x, t) - это полупрямая с угловым коэффициентом

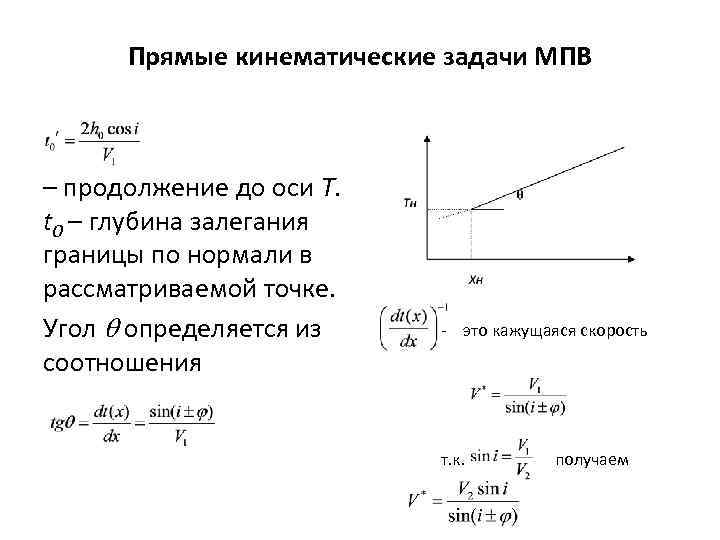Прямые кинематические задачи МПВ – продолжение до оси T. t 0 – глубина залегания границы по нормали в рассматриваемой точке. Угол определяется из соотношения - это кажущаяся скорость т. к. получаем

Прямые кинематические задачи МПВ Поскольку критический угол сохраняется постоянным, лучи головной волны в плоскости падения лучей параллельны между собой и, следовательно, их кажущиеся скорости постоянны.

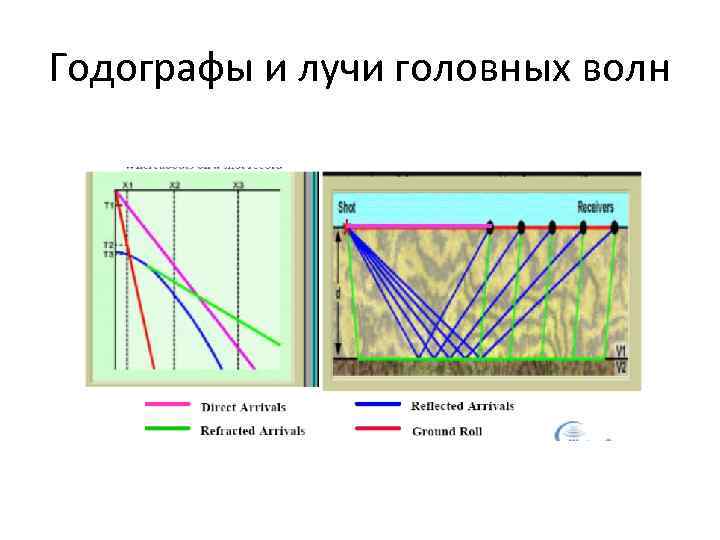Годографы и лучи головных волн

Прямые кинематические задачи МПВ Если вместо слоя рассматривать толщу наклонных пластов, то, используя понятие эффективной скорости для годографа волны, преломленной на подошве этой толщи, имеем где

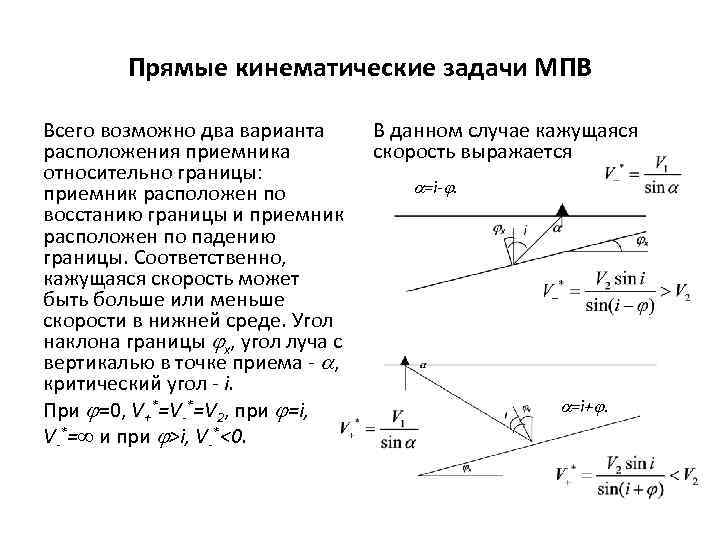Прямые кинематические задачи МПВ Всего возможно два варианта расположения приемника относительно границы: приемник расположен по восстанию границы и приемник расположен по падению границы. Соответственно, кажущаяся скорость может быть больше или меньше скорости в нижней среде. Угол наклона границы x, угол луча с вертикалью в точке приема - , критический угол - i. При =0, V+*=V-*=V 2, при =i, V-*= и при >i, V-*<0. В данном случае кажущаяся скорость выражается =i-. =i+.

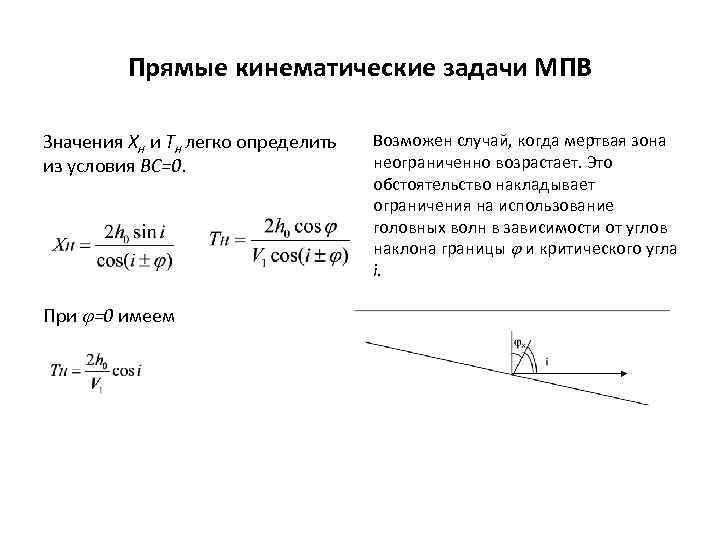Прямые кинематические задачи МПВ Значения Xн и Tн легко определить из условия BC=0. При =0 имеем Возможен случай, когда мертвая зона неограниченно возрастает. Это обстоятельство накладывает ограничения на использование головных волн в зависимости от углов наклона границы и критического угла i.

Получение глубины преломляющей границы и граничной скорости по годографам головных волн Существует несколько способов восстановления характеристик среды по годографам преломленных волн. Один из способов, на котором мы остановимся подробнее – способ T 0. Способ T 0 – приближенный способ, применяемый в методе средних скоростей, когда покрывающая толща характеризуется постоянной средней скоростью Vср. Условия применимости этого метода: • радиус кривизны преломляющей границы значительно больше глубины ее залегания; • граничная скорость меняется плавно Vгр; • проницание отсутствует. При интерпретации способом T 0 мы должны иметь четыре годографа – прямой, встречный и два нагоняющих. В случае если мы считаем среду горизонтально-слоистой с постоянной граничной скоростью, можно рассчитать значения V 2 и h 0 только по одному годографу по формуле Иначе – четыре годографа

Пикировка первых вступлений

Получение глубины преломляющей границы и граничной скорости по годографам головных волн Обычно у нас имеются встречные годографы, соответствующие ПВ 1 и ПВ 2, увязанные во взаимных точках, где время равно T. Вследствие ошибок, допущенных на предыдущих этапах при определении времен вступления, взаимные точки находятся не на одном уровне, необходимо увязать встречные годографы путем уравнивания взаимных времен и разброса ошибки между каналами. Фантоминг – опускание нагоняющего годографа до совмещения в последней точке. У нас имеется «мертвая зона» на участке, где головная волна в первых вступлениях не наблюдается (до критического угла), поэтому фантоминг помогает восстановить этот участок. Если годографы имеют «неровности» и форма этих неровностей повторяется и на нагоняющих годографах, то это связано с особенностями строения среды, а не шумом. Если эти отклонения хаотичны, то это ошибки корреляции. В случае вертикально-неоднородной среды, годографы не подобны, а сближаются. Это не головные, а рефрагированные волны и обработка происходит другим способом. В дальнейшем будем рассматривать однородно-слоистые среды. В результате фантоминга у нас получилось два сводных годографа. В случае если годографы строго прямые и пересекаются в центре, границы строго горизонтальны.

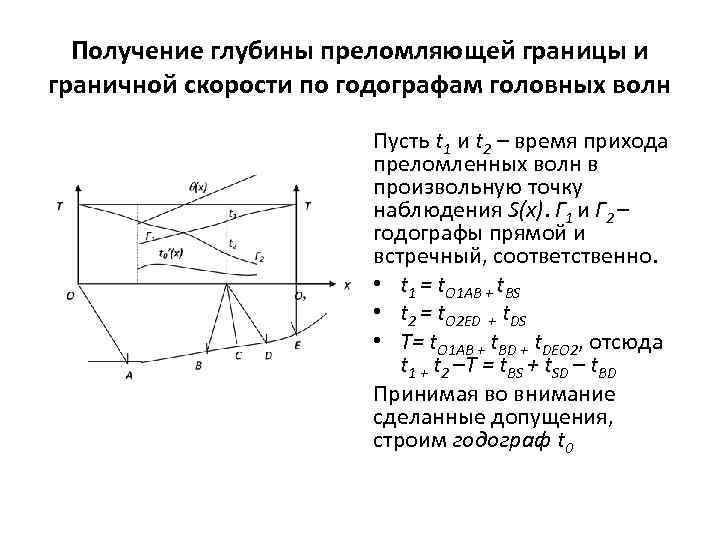Получение глубины преломляющей границы и граничной скорости по годографам головных волн Пусть t 1 и t 2 – время прихода преломленных волн в произвольную точку наблюдения S(x). Г 1 и Г 2 – годографы прямой и встречный, соответственно. • t 1 = t. O 1 AB + t. BS • t 2 = t. O 2 ED + t. DS • T= t. O 1 AB + t. BD + t. DEO 2, отсюда t 1 + t 2 –T = t. BS + t. SD – t. BD Принимая во внимание сделанные допущения, строим годограф t 0

Получение глубины преломляющей границы и граничной скорости по годографам головных волн t. BS = t. DS = t. BD = 2 t. DC = = Далее, по формуле для годографа, учитывая t’ 0=t 1+t 2 -T= = Таким образом, эхоглубина h=k* t 0’=k (t 1+t 2 -T)

Получение глубины преломляющей границы и граничной скорости по годографам головных волн Для вычисления k надо знать Vгр и Vср (по годографу прямой волны). Разностный годограф (x)=t 1 -t 2+T; Напишем выражения для прямого и встречного годографов: годограф слева. Здесь h 1 – эхоглубина под ПВ слева годограф справа. Здесь h 2 – эхоглубина под ПВ справа. l – взрывной интервал. x – координата точки наблюдения. Найдем

Получение глубины преломляющей границы и граничной скорости по годографам головных волн Ремарка: знак «+» берется в случае, если приемник располагается по падению, знак «-» если по восстанию границы. (приемник по падению границы), (приемник по восстанию границы). Вспомним из тригонометрии, что sin(i+ )=sini cos + sin cosi sin(i- )=sini cos - sin cosi Граничную скорость можно определить по приближенной формуле (погрешность зависит от угла наклона границы ). При изменении граничной скорости вдоль профиля разностный годограф будет криволинейным. Данная формула справедлива для небольшого угла наклона границы (до 20 ).

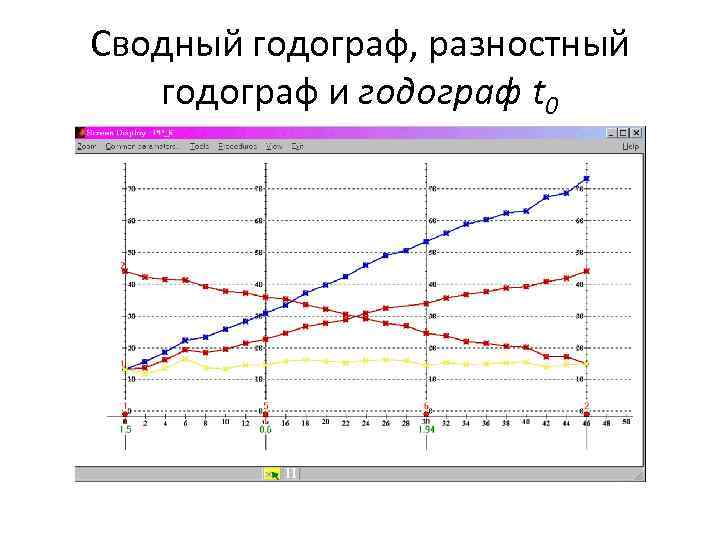Сводный годограф, разностный годограф и годограф t 0

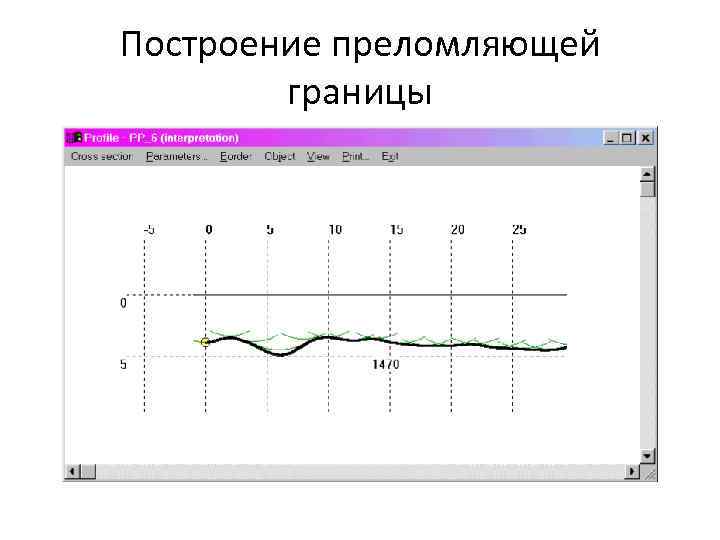Построение преломляющей границы

Получение глубины преломляющей границы и граничной скорости по годографам головных волн Способ построения разностного годографа позволяет определить Vгр во второй среде с ошибкой менее 6% при угле наклона границы менее 20. Не всегда можно получить полную 4 точечную систему наблюдений. После определения скорости строим границу методом засечек. По вычисленным эхоглубинам строим преломляющую границу как огибающую семейства окружностей, проведенных из точек наблюдения соответствующими радиусами. Если поверхность, разделяющая однородное полупространство и слой, не плоская, но известно, что Vср мало меняется, то годограф не будет прямолинейным. т. е. = (x). Если из геологических данных известно, что преломляющая граница плоская и скорость V 1 не меняется, то непрямолинейность годографа преломленных волн будет указывать на изменение Vгр. По одному годографу можно определить только кажущуюся скорость V*.

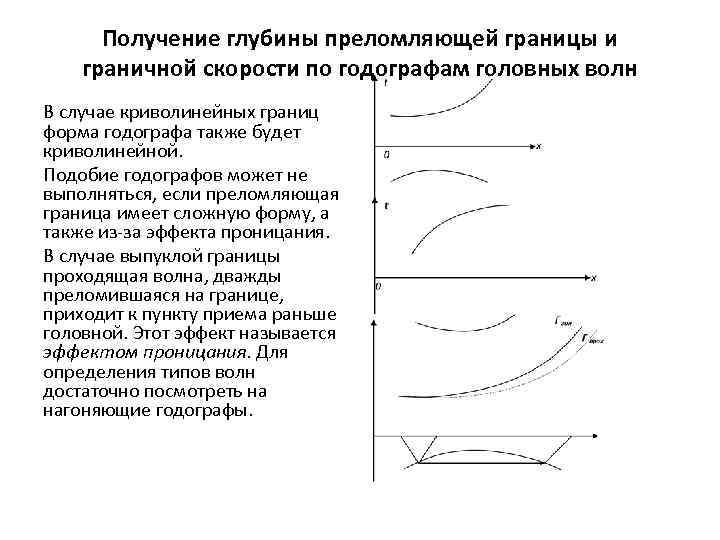Получение глубины преломляющей границы и граничной скорости по годографам головных волн В случае криволинейных границ форма годографа также будет криволинейной. Подобие годографов может не выполняться, если преломляющая граница имеет сложную форму, а также из-за эффекта проницания. В случае выпуклой границы проходящая волна, дважды преломившаяся на границе, приходит к пункту приема раньше головной. Этот эффект называется эффектом проницания. Для определения типов волн достаточно посмотреть на нагоняющие годографы.

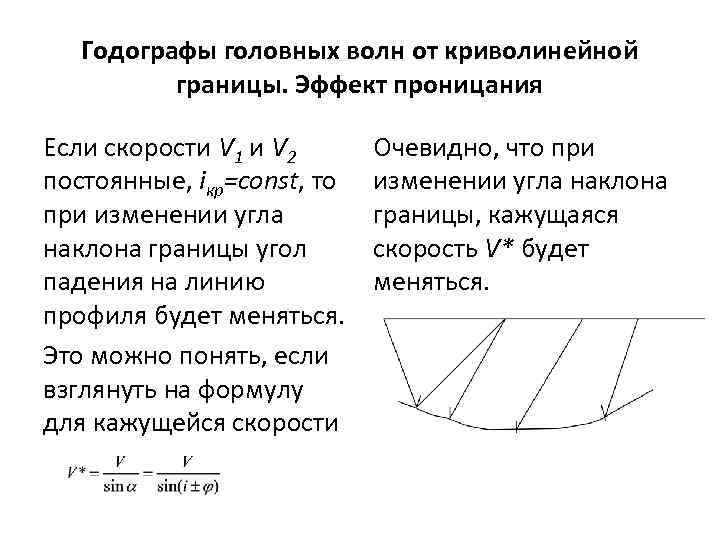Годографы головных волн от криволинейной границы. Эффект проницания Если скорости V 1 и V 2 постоянные, iкр=const, то при изменении угла наклона границы угол падения на линию профиля будет меняться. Это можно понять, если взглянуть на формулу для кажущейся скорости Очевидно, что при изменении угла наклона границы, кажущаяся скорость V* будет меняться.

Назовите условие образования головных волн. Почему головные волны также называются коническими? Что представляет собой годограф головной волны? В каком случае головная волна не выйдет на поверхность? Каковы условия применения способа обработки T 0? Как можно определить граничную скорость по годографу головной волны в случае горизонтальной границы?