Метод последовательных приближений Выполнили: Шарипов К. Енгай В. Базарбаев Б. Омар С.
Приближенное решение уравнений Виды уравнений: линейные, квадратные, иррациональные, показательные, логарифмические, тригонометрические. При их решении используют общие формулы, позволяющие выразить корни уравнения через входящие в это уравнение числа. Например, для уравнения вида ax+b=0, a≠ 0, решение есть формула x=–b/a, для ax 2+bx+c=0, a≠ 0, - формула x 1, 2=(-b±√b 2 -4 ac)/2, для уравнения cosx=a, │a│≤ 1, - формула x=±arccosa + 2πn, nϵ Z.
Для уравнений вида 2 x=x+3, x=1+sin 3 x/10 и т. д. нет общих формул решения. Однако, для решения практических задач надо уметь решать такую задачу: Дано уравнение f(x)=0, имеющее корни x 1 , x 2 , …, xn , и число ε>0. Найти числа t 1 , t 2 , …, tn , отличающиеся от корней этого уравнения меньше чем на ε, т. е. такие, что │tk-xk│< ε, 1≤ k ≤ n. Решение указанной задачи является одним из вопросов вычислительной математики.
Наиболее важный метод приближенного решения уравнений – метод последовательных приближений, применяемый при решении уравнений, записанных в виде x=ϕ (x). Уравнение x 2 -2=0 можно записать в следующих видах: x=(x 2+2)/2 x, x=(3 x 2+2)/4 x, x=(10 x(2 -x 2)+x 2+2)/2 x.
Для начала выбирают некоторое начальное приближение x 1 и подставляют его вместо x в ϕ(x), тогда значение x 2=ϕ (x 1) – второе приближение и x 3=ϕ (x 2) и т. д. Последовательность x 1, x 2, … имеет предел α. Если функция ϕ непрерывна , из равенства xn+1= ϕ(xn) вытекает, что lim xn+1= lim ϕ(xn) = ϕ(lim xn) n→∞ n→∞ Т. е. α=ϕ(α). Это означает, что α является решением уравнения x=ϕ(x). При достаточно больших значениях n разность │xn-α│становится сколь угодно малой, т. е. xn является достаточно хорошим приближением для искомого корня.
Для извлечения квадратных корней применяется следующий метод: берем какое-нибудь положительное приближение x для √a и строим последовательность x 1, x 2, …, xn, …, где xn+1=(a+xn 2)/2 xn Процесс ведется до тех пор, пока модуль разности значений xn+1 и xn не станет меньше заданной точности вычислений.
Для вычисления корней k-й степени уравнение xk=a записывают в виде: X=(a+(k-1)xk)/kxk-1. Далее вычисления ведутся по формуле xn+1=(a+(k-1) xnk)/ xnk-1.
Условие сходимости Метод последовательных приближений не всегда приводит к сходящейся последовательности чисел. Условие сходимости метода последовательных приближений: Теорема. Пусть на отрезке [a, b ] функция f монотонна, причем отрезок [f(a), f(b) ] является частью отрезка [a, b ] , и пусть существует такое число q , что 0<q<1 и |f’ (x) | ≤ q на отрезке [a, b ]. Тогда на этом отрезке лежит единственный корень уравнения x=f (x), причем процесс последовательных приближений, начинающихся с любого значения c из [a, b ], сходится к этому корню.
Пример № 1 Найдем методом последовательных приближений корень уравнения x=1+(arctgx)/2 точностью до 0. 001. Пример № 2 Решить уравнение 10 x-1 -cosx=0 ? Пример № 3 Найдем значение √ 5 с точностью до 0. 001. Пример № 4 Найдем с точностью до 0. 001 значение 3√ 970.
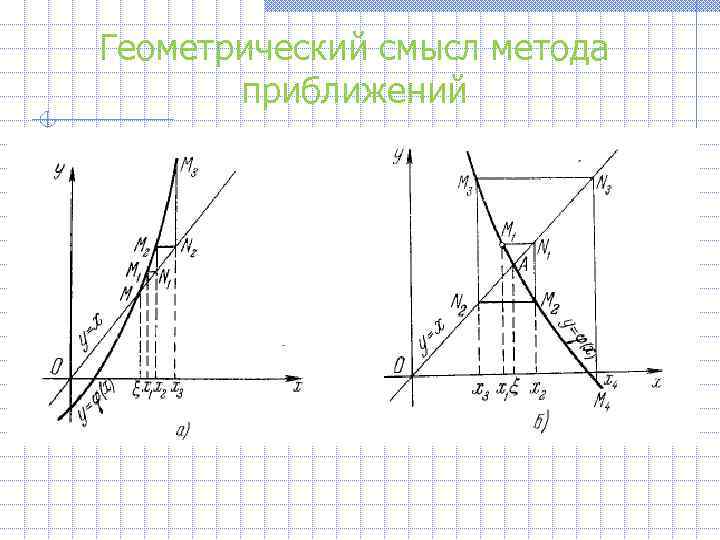
Геометрический смысл метода приближений
Скачать презентацию Метод последовательных приближений Выполнили Шарипов К Енгай В
метод последовательных приближений.pptx