Метод последовательной детализации 1 Написать программу вычисления

Метод последовательной детализации

1+ Написать программу вычисления

Исходные данные: ( x , n). Результаты ( сумма. Обозначим Y ). Этого достаточно, чтобы можно было сделать первый набросок программы. Program P 1; Var x : real; // аргумент n : integer; // количество слагаемых в сумме y : real; // сумма begin write (‘ введите аргумент x и кол-во слагаемых n ‘); readln(x, n); y: =0; { P 2 – вычисление суммы и присвоение ее y} Write(‘сумма равна ‘, y) End.

// P 2 – вычисление суммы и присвоение ее y Program P 2; Var x : real; // аргумент n : integer; // количество слагаемых в сумме y : real; // сумма i : integer; // номер обрабатываемого слагаемого begin y: =0; for i: =1 to n do begin { вычислить числитель и результат поместить в a} { вычислить знаменатель и результат поместить в b } y: =y+a/b; Write(‘сумма равна ‘, y) End.

Program P 31; Var x : real; // аргумент i : integer; //показатель степени j : integer; // счетчик умножений a : real; // числитель begin a: =1; for j : =1 to i do a : = a*x end.

Program P 32; Var i : integer; //число, факториал которого вычисляется j : integer; // счетчик умножений b : real; // знаменатель begin b: =1; for j : =1 to i do b : = b*j end.

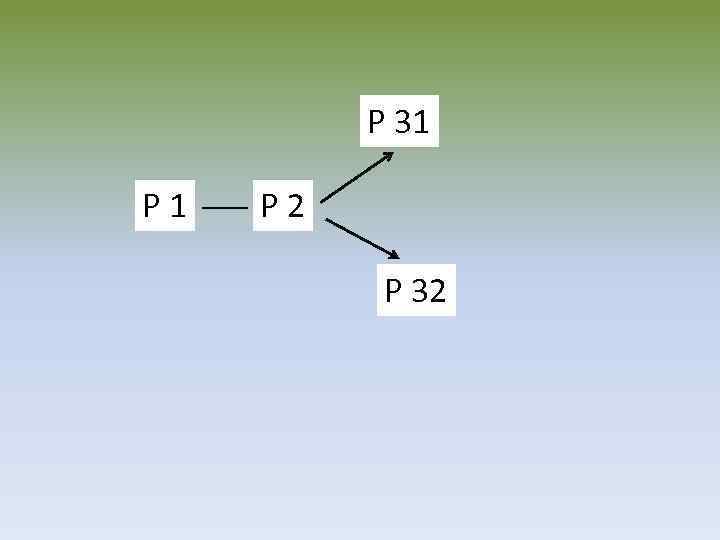P 31 P 2 P 32

Program Task_1; Var x : real; // аргумент n : integer; // количество слагаемых в сумме y : real; // сумма i : integer; // номер обрабатываемого a : real; b : real; слагаемого // числитель обрабатываемого слагаемого // знаменатель обрабатываемого слагаемого j : integer; // счетчик умножений Begin write (‘ введите аргумент x и количество слагаемых n ‘); readln(x, n);

// P 2 – вычисление суммы и присвоение ее y y: =0; for i : = 1 to n do begin a : = 1; for j : = 1 to i do a : = a*x b : = 1; for j : =1 to i do b : = b*j y: =y+a / b; Write(‘сумма равна ‘, y) End.

Program Task_2; Var x: real; // аргумент n : integer; // количество слагаемых в сумме y : real; // сумма // функция для вычисления числителя Function a(x : real; i : integr) : real; Var j : inteder ; //счетчик умножений begin a: =1; for j: =1 to i do a : = a*x end;

// функция для вычисления знаменателя Function b(i : integer) : real; var j : integer; // счетчик умножений begin b : =1; For j : = 1 to i do b : =b*j end; // функция вычисления суммы Function y(x : real; n : integer) : real; var i : integer; // номер очередного слагаемого begin y : =0; For i : = 1 to n do y : = y + a(x, i)/b(i) end;

// основная программа Begin write(‘ Введите аргумент – x и количество слагаемых‘); readln(x, n); write (‘ Сумма равна ‘, y(x, n)) end.

Решение 3. Предыдущий способ решения не лишен недостатков. Например, при вычислении 5! Заново вычисляются 2!, 3!, 4!, а при вычислении x^5, x^4, x^3, x^2 заново приходится вычислять предыдущие значения произведений. Чтобы избежать этого , каждое слагаемое задаем формулой U(k) = x^k / k!. Найдем отношение U(i) / U(i - 1): ): U(i) / U(i - 1) = [ x ^ i * (i - 1)! ] / i! * x ^ (i – 1)] = x / i. отсюда U(i) = x / i * U(i - 1).

Program Task_3; Var x : real; // аргумент n : integer; // количество слагаемых в сумме y : real; // сумма i : integer; // номер обрабатываемого слагаемого u : real; // очередное слагаемое Begin write (‘введите аргумент x и кол-во слагаемых n ‘); readln(x, n); y : = 0; u : =1; i : = 1; while i <= n do begin y : =y + u; u : = u*x / i; i : =i + 1; end; write (‘ Сумма равна ‘, y) End.