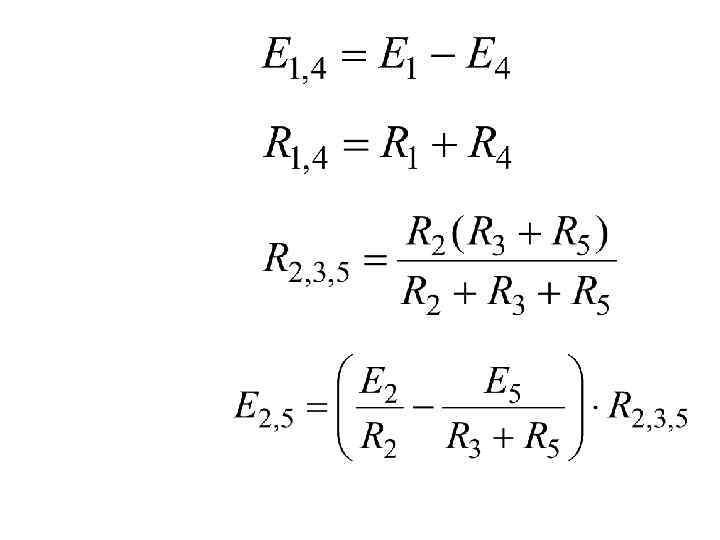Метод контурных токов Применяется для расчета сложных

Метод контурных токов

Применяется для расчета сложных схем с целью определения неизвестных токов и основан на законах Кирхгофа

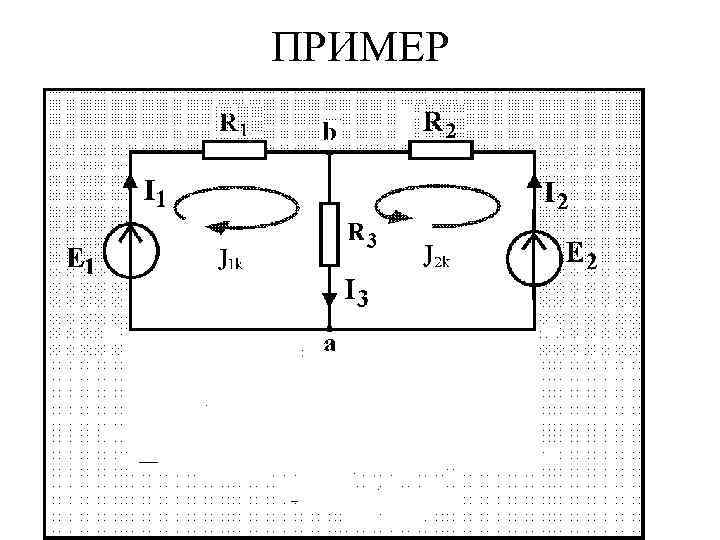ПРИМЕР

Система уравнений по законам Кирхгофа

Обозначим токи внешних ветвей, как контурные токи, каждый из которых замыкается по ветвям своего контура:

Подставляя в 2 и 3 получим уравнения по методу контурных токов:

Порядок расчета • 1. Задаем токи ветвей схемы. • 2. Направляем контурные токи так, чтобы они хотя бы по одному разу проходили через каждую ветвь. • 3. Через источник тока должен проходить единственный контурный ток, который будет равен величине тока источника тока. • 4. Для каждого неизвестного контурного тока составляем уравнение по правилу: • контурный ток умножается на алгебраическую сумму сопротивлений своего контура.

• Контурные токи соседних контуров умножаются на смежные с данным контуром сопротивления со знаком + (если контурные токи совпадают по направлению) или - ( если не совпадают). В правой части уравнения пишется алгебраическая сумма ЭДС данного контура. • 5. После расчета контурных токов определяются токи ветвей схемы и составляется баланс мощности

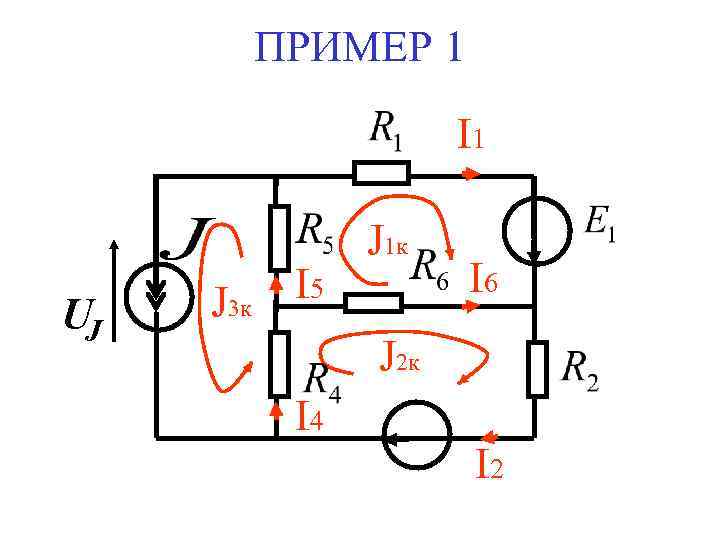ПРИМЕР 1 I 1 UJ J 3 к I 5 J 1 к I 6 J 2 к I 4 I 2

Составляем уравнения: Определяем токи ветвей схемы:

Напряжение на источнике тока: Баланс мощности. мощность источников: потребляемая мощность: Небаланс:

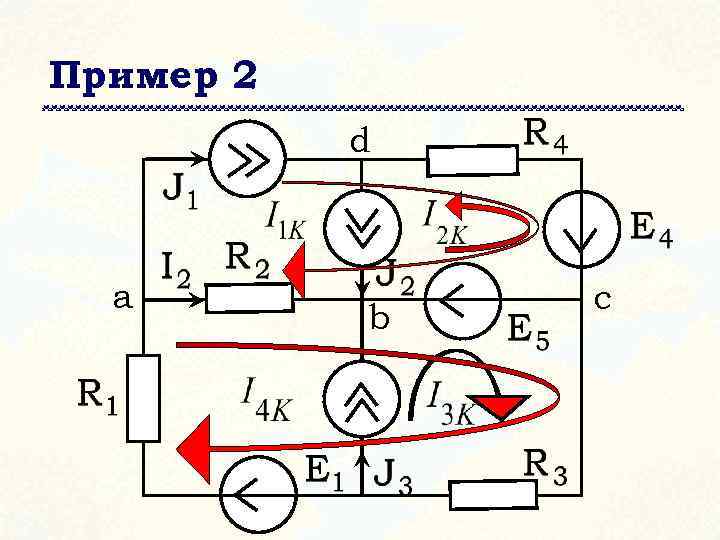Пример 2 d a b c

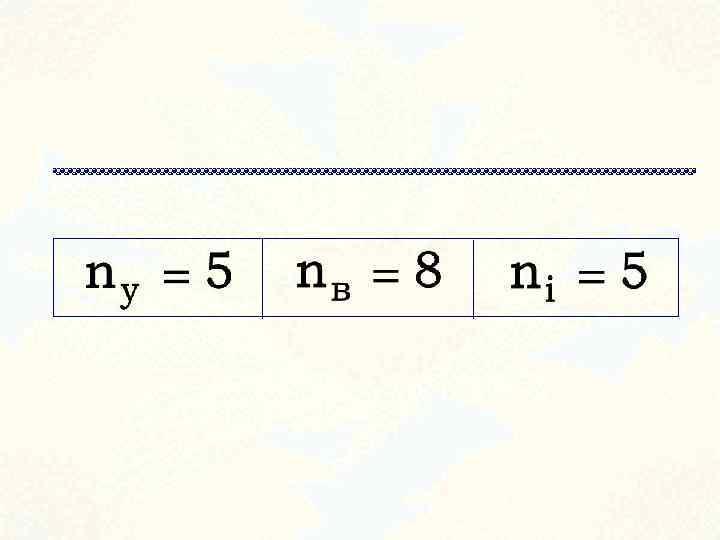
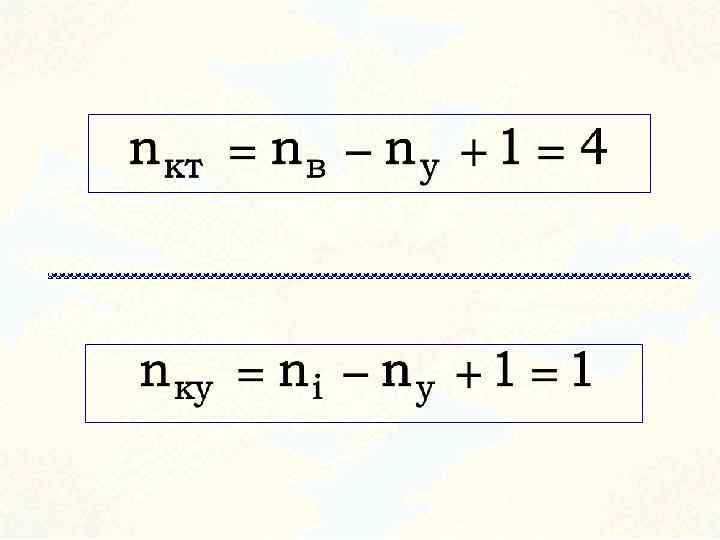
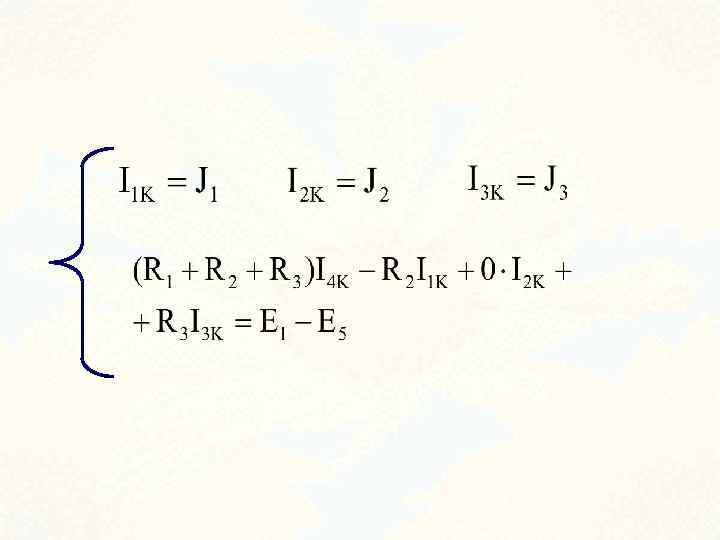
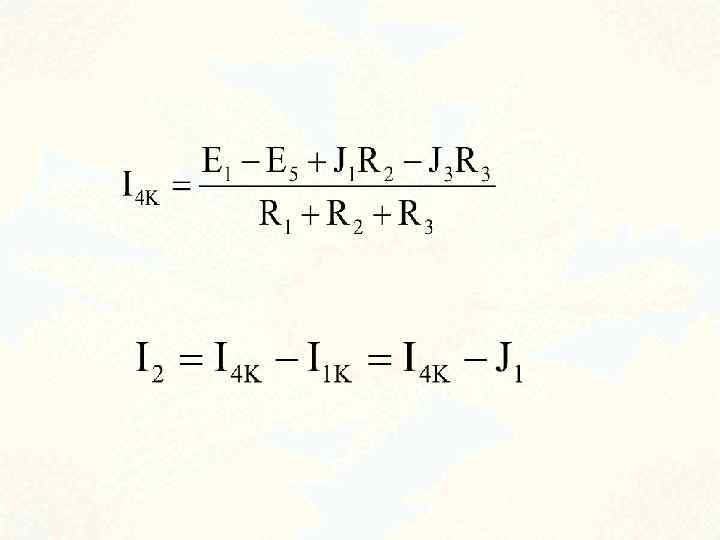
Таким образом по методу контурных токов необходимо решить значительно меньше уравнений по сравнению с методом законов Кирхгофа

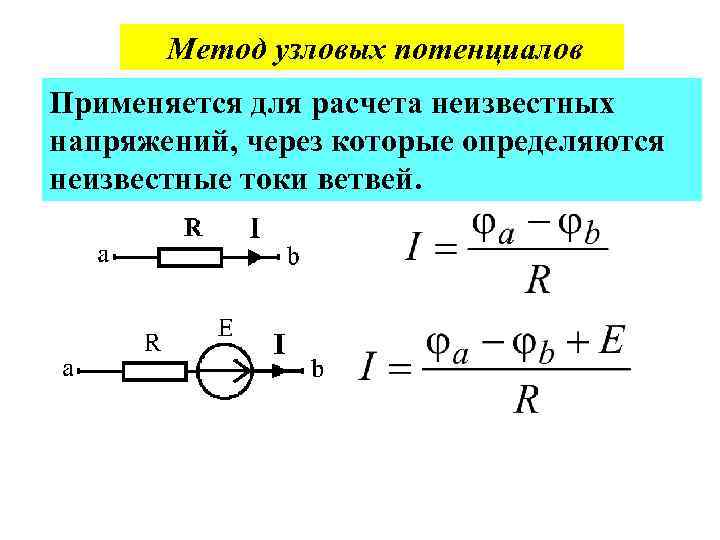Метод узловых потенциалов Применяется для расчета неизвестных напряжений, через которые определяются неизвестные токи ветвей.

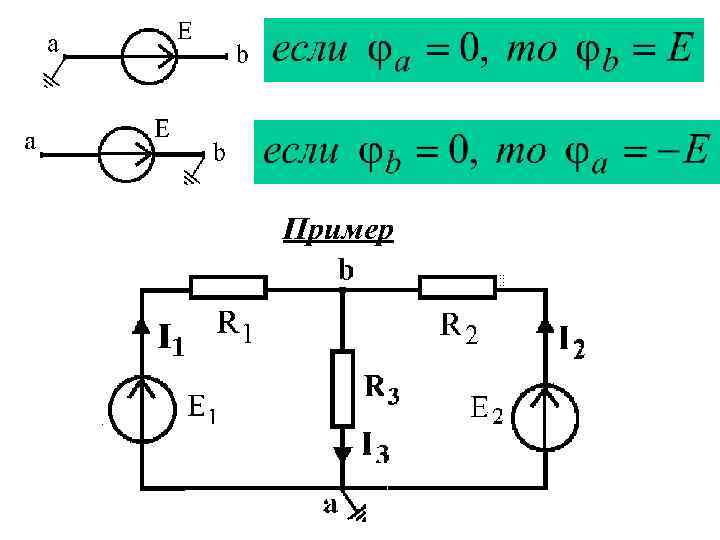Пример

По первому закону Кирхгофа для узла b: Выразим токи ветвей через потенциалы узлов:

С учетом того, что получим уравнение: Порядок расчета 1. Задаем направления токов ветвей схемы; 2. Выбираем узел с нулевым потенциалом; 3. Для каждого узла с неизвестным потенциалом составляем уравнение по правилу:

потенциал данного узла умножается на алгебраическую сумму проводимостей ветвей подходящих к данному узлу ( произведение берется со знаком +). Потенциалы соседних узлов умножаются на проводимости ветвей соединяющих соседний узел с данным узлом (произведения берутся со знаком -). В правой части уравнения пишется алгебраическая сумма произведений подходящих к данному узлу источников ЭДС на проводимости своих ветвей, а также алгебраическая сумма источников тока со знаками + или - ( + берется, если источники направлены в данный узел).

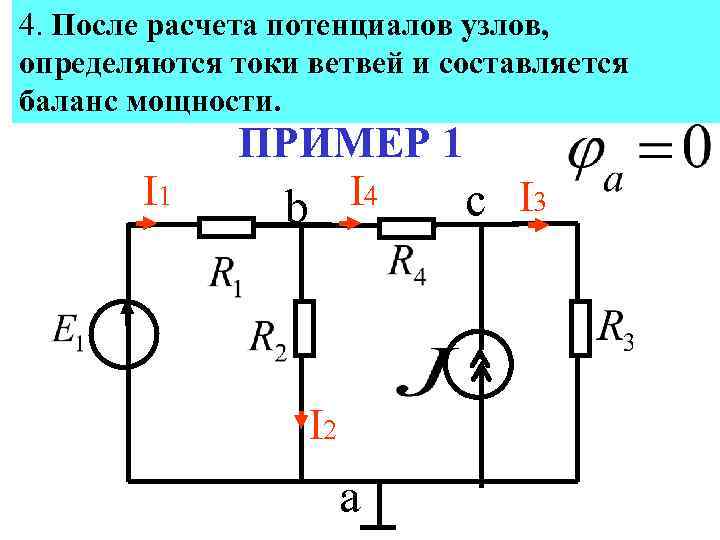4. После расчета потенциалов узлов, определяются токи ветвей и составляется баланс мощности. I 1 ПРИМЕР 1 I 4 c I 3 b I 2 a

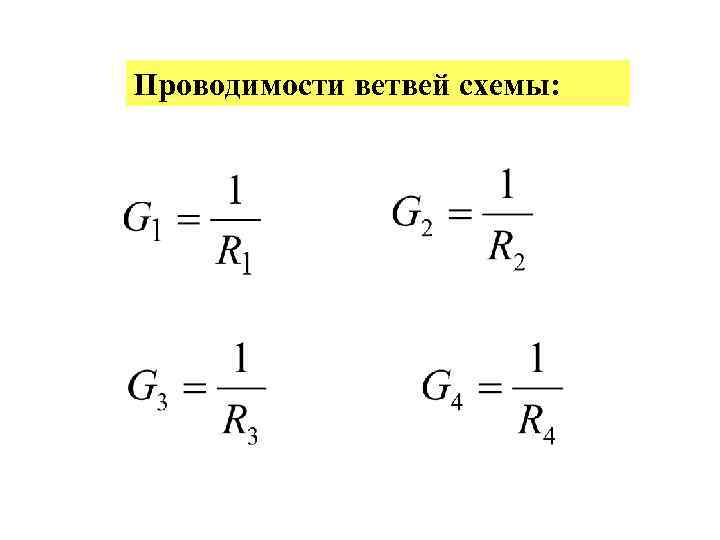Проводимости ветвей схемы:

Для неизвестных потенциалов составляем уравнения: Токи ветвей схемы:

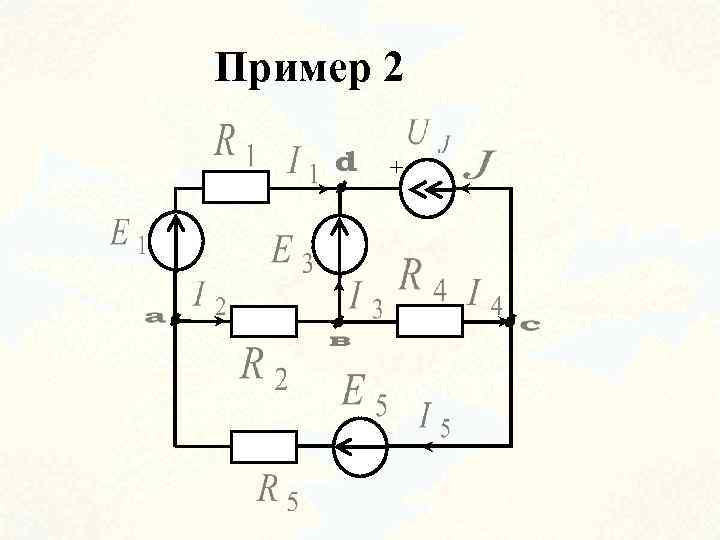Пример 2 +

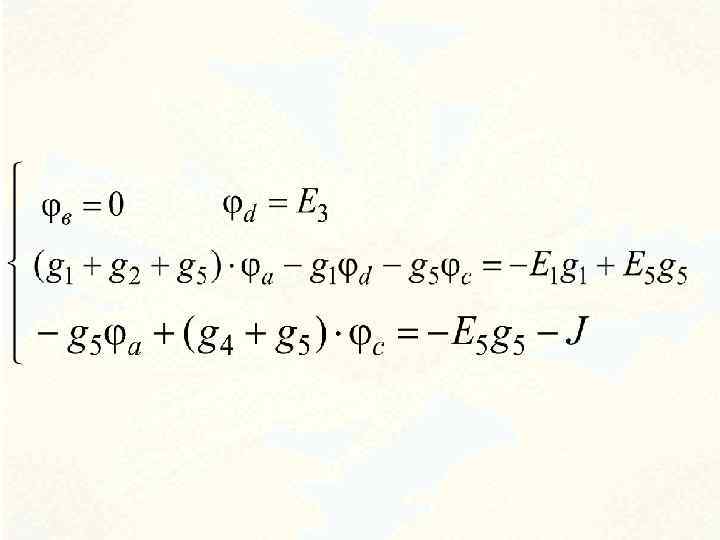
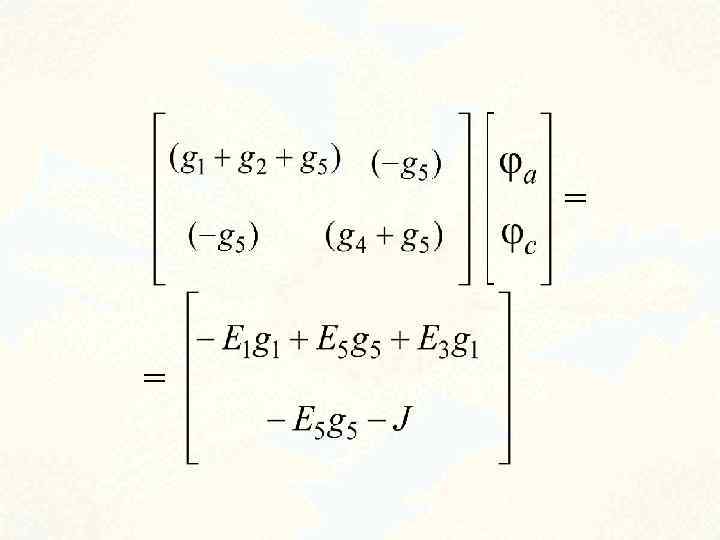é ê ê ê ê ë = =

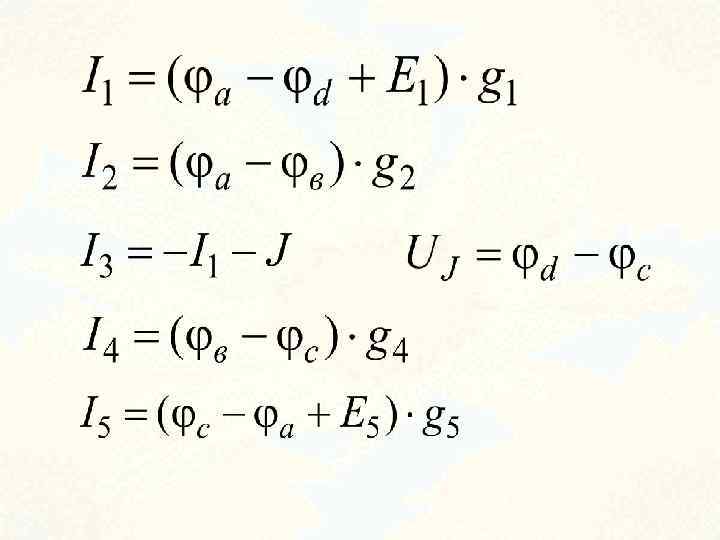
Метод преобразований

Этот метод основывается на правилах преобразований линейных цепей

Преобразования схем используются для их упрощения и могут быть доказаны при помощи законов Ома и Кирхгофа. Приведем правила преобразований без доказательства

1. Правило распределения (разброса) тока в параллельных ветвях

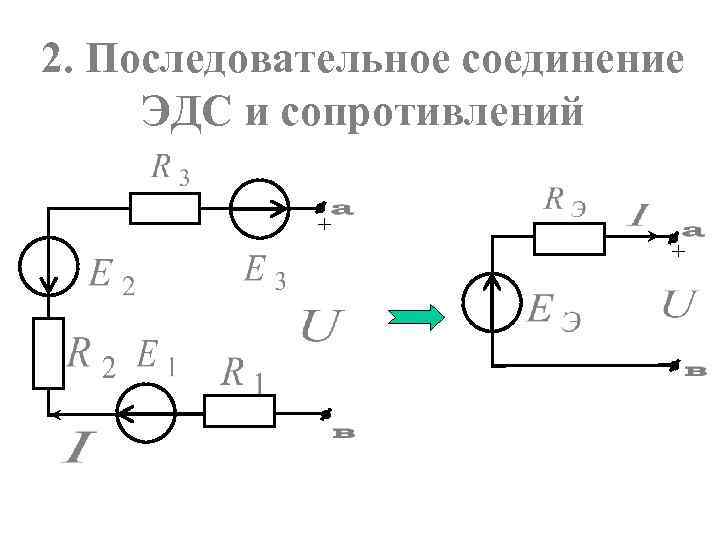2. Последовательное соединение ЭДС и сопротивлений + +

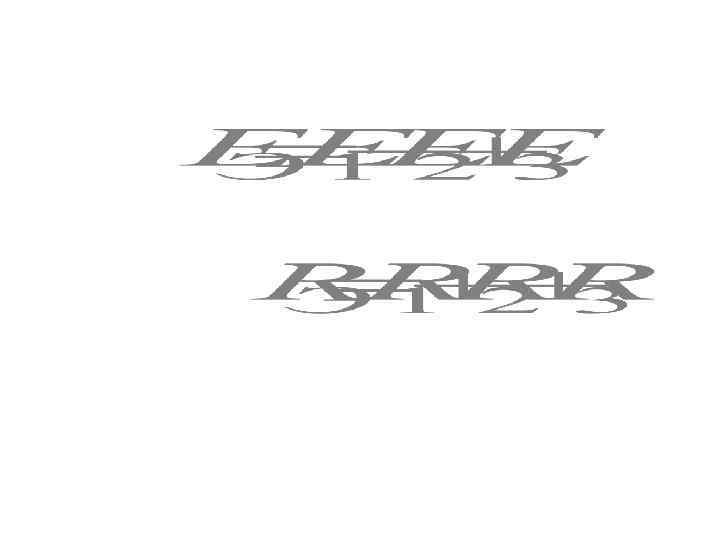
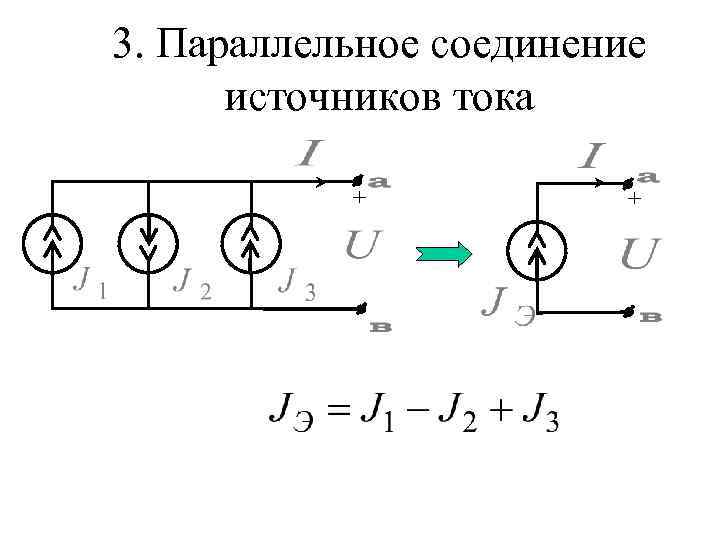3. Параллельное соединение источников тока + +

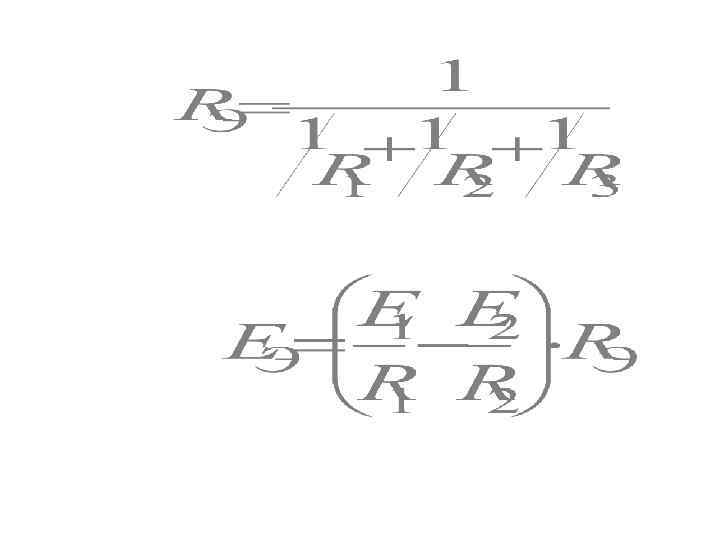
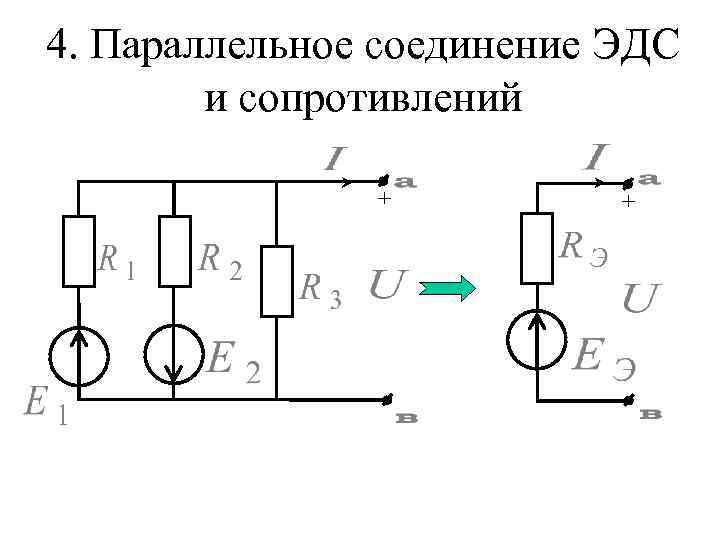4. Параллельное соединение ЭДС и сопротивлений + +

5. Замена источника тока на источник ЭДС и наоборот + +

6. Преобразование треугольника в звезду и наоборот

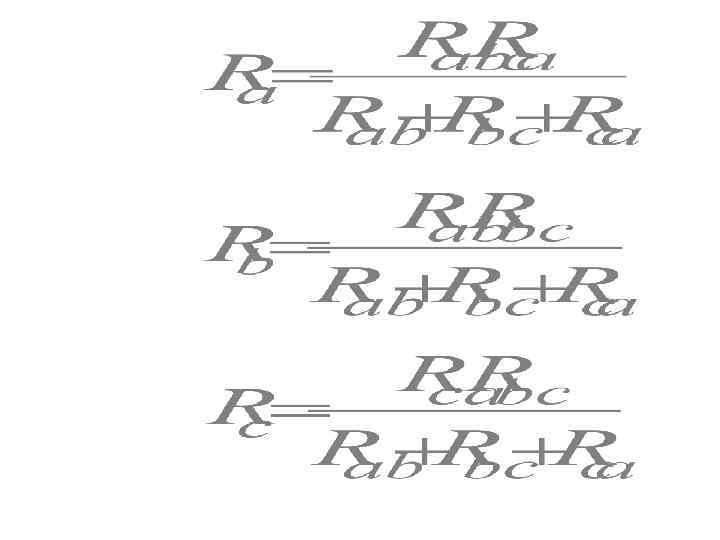
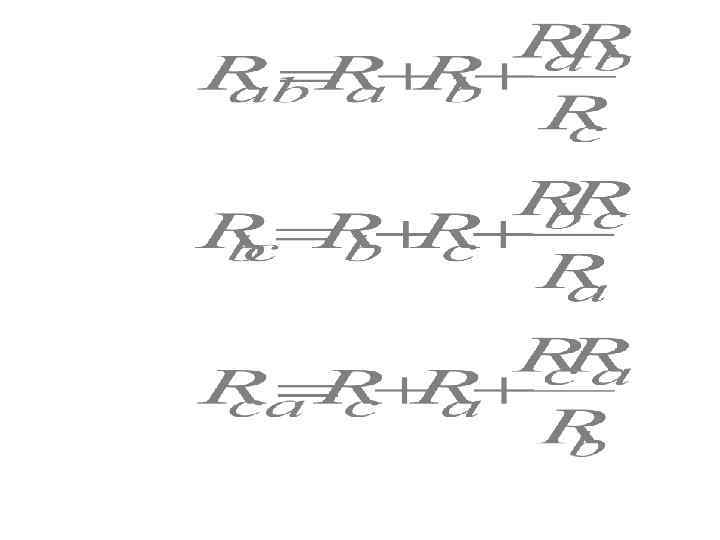
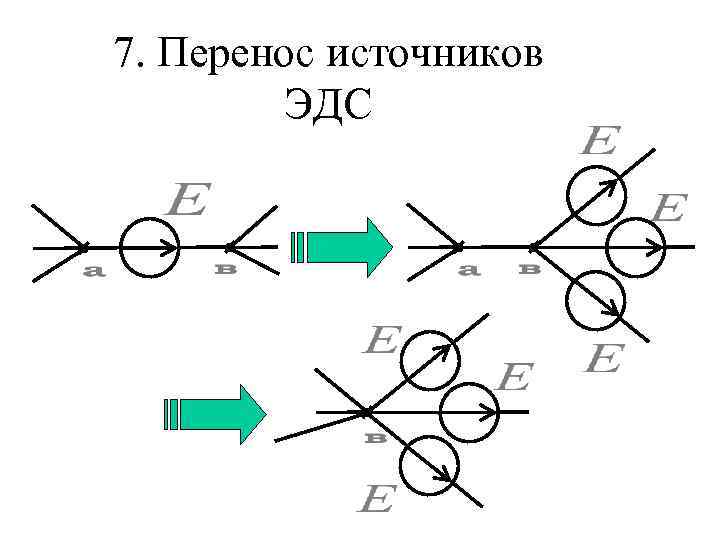7. Перенос источников ЭДС

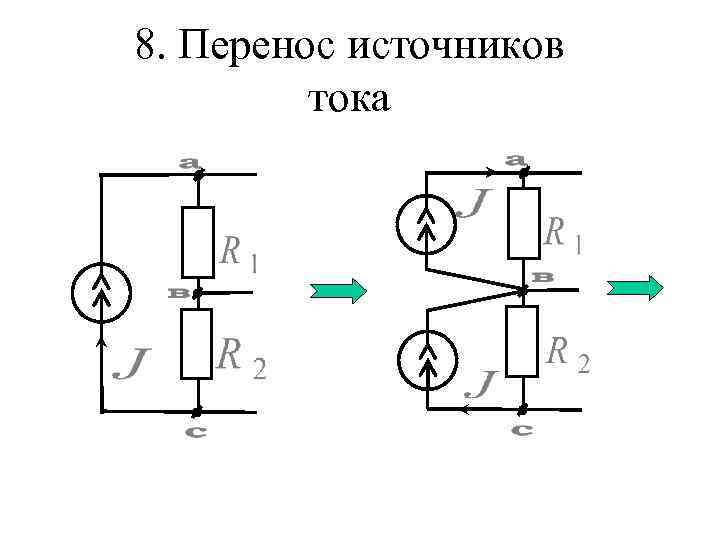8. Перенос источников тока

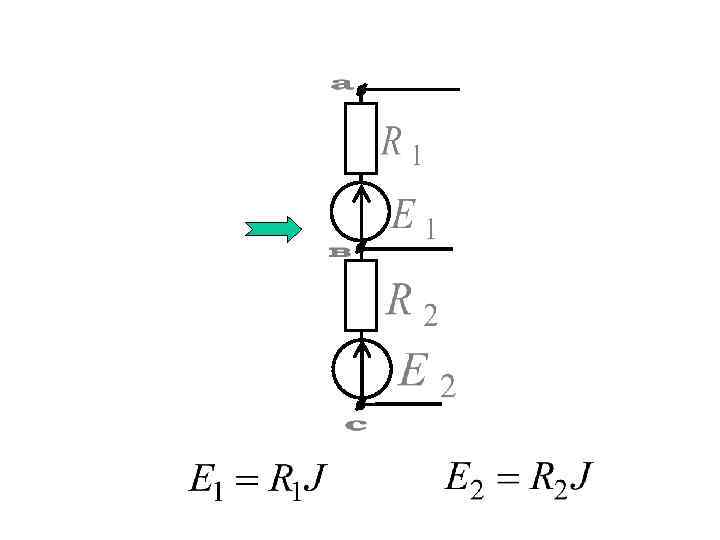
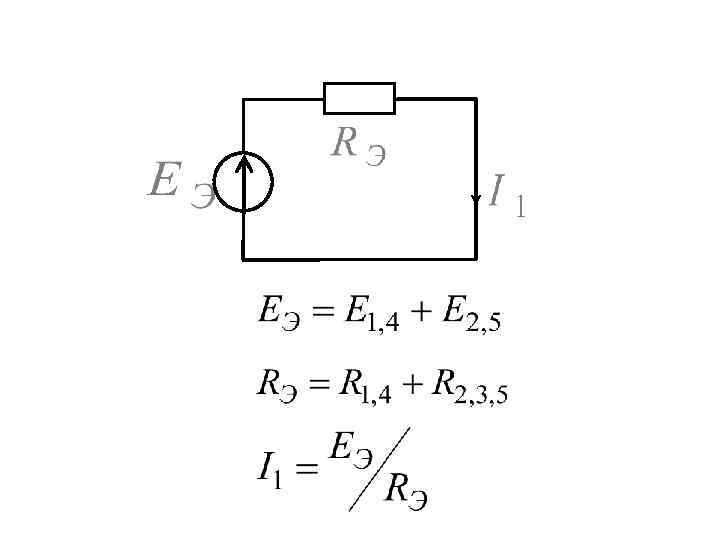
На основе приведенных правил можно реализовать метод преобразований для расчета тока или напряжения в к-ветви схемы. Для этого схема преобразуется до одного контура с искомым током или напряжением, где эти величины легко определяются

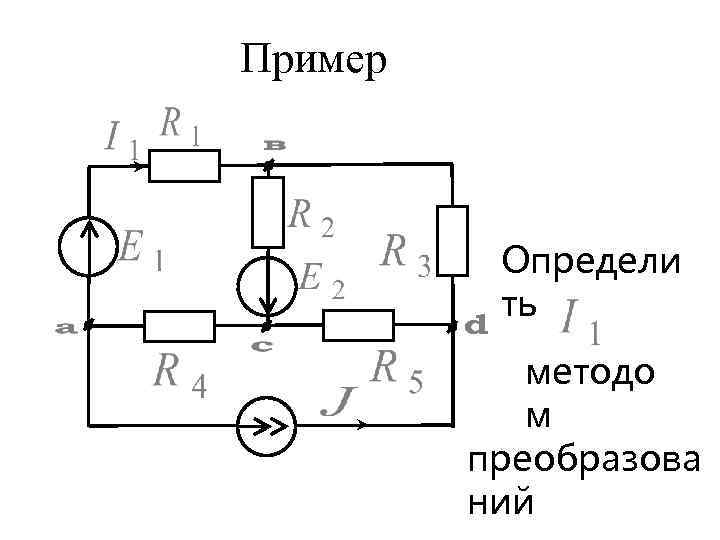Пример Определи ть методо м преобразова ний

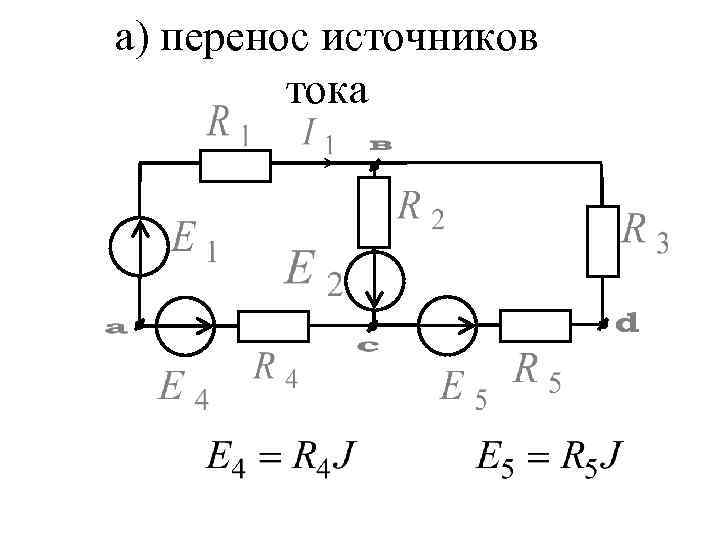а) перенос источников тока

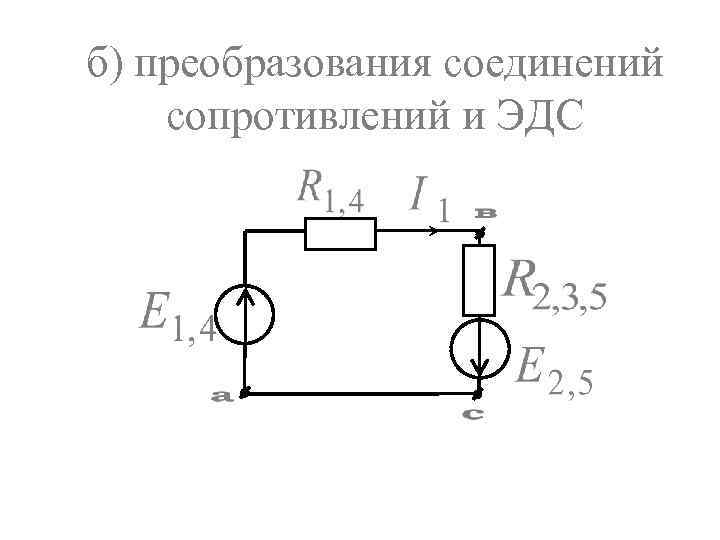б) преобразования соединений сопротивлений и ЭДС