Метод Форстера-Стюарта H 0 отсутствие тренда в структуре

Метод Форстера-Стюарта H 0: отсутствие тренда в структуре ряда. Вспомогательные функции: ; . Где: T – общий временной интервал, Проверяется гипотеза о том, что L=0. Для проверки строится t-статистика, которая имеет распределение Стьюдента с t-1 степенями свободы: , где . Гипотеза об отсутствии тенденции отклоняется, если расчетное значение больше табличного на выбранном уровне значимости 0, 95. 1

Подходы в оценке тренда • оценка тренда с помощью гладких функций f(t) – параметрические методы оценки тренда (методы аналитического выравнивания); • оценка тренда на основе различного рода скользящих средних – непараметрические методы (методы механического сглаживания). 2

Оценка тренда на основе функций • Подбор аналитической функции, удовлетворительно описывающей значение уровней ряда на всем интервале наблюдений. • Оценка тренда на основе функций f(t) выполняется как оценка параметров нелинейной регрессии , то есть зависимость исследуемого показателя mt от фактора времени. 3

Пример оценки тренда Пусть тренд имеет вид полиномиальной регрессионной зависимости: . Задача определения тренда по временному ряду x 1, x 2, …, xn сводится к оценке параметров a 0, a 1, …, ap. Применяем метод наименьших квадратов. 1) Минимизируем сумму квадратов отклонений между расчетными и фактическими значениями: (xt-a 0 -a 1 t-a 2 t 2 -…-aptp)2 min. 2) Для определения минимума, находим частные производные по aj (j=0, . . , p) и приравнивают их к нулю. Получаем систему из p+1 уравнений, разрешая которую получаем выражение для коэффициентов aj (j=0, …, p). 4

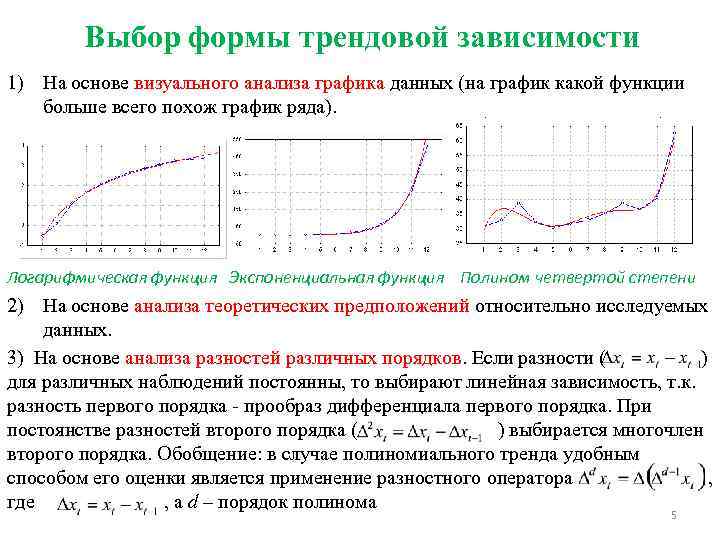Выбор формы трендовой зависимости 1) На основе визуального анализа графика данных (на график какой функции больше всего похож график ряда). Логарифмическая функция Экспоненциальная функция Полином четвертой степени 2) На основе анализа теоретических предположений относительно исследуемых данных. 3) На основе анализа разностей различных порядков. Если разности ( ) для различных наблюдений постоянны, то выбирают линейная зависимость, т. к. разность первого порядка - прообраз дифференциала первого порядка. При постоянстве разностей второго порядка ( ) выбирается многочлен второго порядка. Обобщение: в случае полиномиального тренда удобным способом его оценки является применение разностного оператора , где , а d – порядок полинома 5

Метод Скользящих средних Поскольку любая гладкая функция при самых общих допущениях может быть локально представлена полиномом с довольно высокой степенью точности, предпочтительной является следующая процедура. Подбираем полином к первой группе из 2 m+1 членов ряда и используем этот полином для определения значения тренда в m+1 -ой, средней точке группы. Затем подбираем полином того же порядка к группе, состоящей из второго, третьего, …, 2 m+2 наблюдения, и находим значение тренда в m+2 точке и так далее для всех членов ряда до последней группы из 2 m+1 членов. Эта процедура эквивалентна линейной комбинации наблюдений с коэффициентами, которые могут быть оценены раз и навсегда. Простейшее скользящее среднее можно вычислить по формуле: (1) Здесь 2 m+1– количество точек, на которых строится скользящее среднее. 6

Пример оценки тренда методом скользящих средних Подбираем полином третьего порядка к группам по семь точек. T = -3, -2, -1, 0, 1, 2, 3. Константы aj находим методом наименьших квадратов, то есть путём минимизации выражения: Дифференцируем выражение по aj, и выписываем уравнения при одинаковых степенях. Получаем систему: (2) 7

Пример оценки тренда методом скользящих средних В системе переносим в левую часть, а суммы с коэффициентами aj в правую часть, причем учитываем, что суммы нечетных порядков t от – 3 до 3 равны 0. (3) Для значения a 0, значения ряда в момент t=0, используем лишь первое и третье из уравнений, получаем: следовательно, значение тренда в какой-либо точке равно средневзвешенному значению семи точек с данной точкой в качестве центральной и весами , или в силу симметричности . 8

Пример оценки тренда методом скользящих средних Рассмотрим конкретный ряд t= 1 2 xt= 0 1 3 8 4 5 6 7 8 9 27 64 125 216 343 512 Значение тренда в точке 4 (t=4) будет: и оно совпадает с соответствующим членом ряда. 9

Общая процедура оценки тренда методом скользящих средних Если к 2 m+1 точкам подбирают полином порядка p, необходимо минимизировать: Минимизация приводит к уравнениям, аналогичным (2), которые разбиваются на две подсистемы, подобные (3). Решение относительно a 0 зависит от численных значений суммы t j и линейных функций от xt типа t j xt. Далее значение тренда в точке t=k вычисляется как взвешенное среднее значение от xk-m до xk+m. 10

Свойства весов 1. Сумма весов равна единице. Это следует из того, что если применить процедуру взвешивания к ряду, все члены которого равны одной и той же константе, то среднее должно равняться этой же константе; 2. Веса симметричны относительно серединного значения. Это следует из того, что они получены, как функции сумм t j xt, которые сами симметричны; 3. Значения тренда не зависят от направления отсчета времени, в силу свойства 2); 4. Для полиномов четного порядка (2 k) формулы будут те же самые, что и для полиномов нечетного порядка (2 k+1); 11

Способы вычисления упрощенных формул, для определения скользящих средних Первый: Записывают формулу на языке разности рядов, особенно когда разности меньше, чем исходные значения ряда. Записывают разность вперед как , так что , и т. д. , получаем, например: Из этого уравнения явно видим разность между рядом и трендом. Второй: рассматривают скользящее среднее как среднее разностей. Например: 12

Способы вычисления упрощенных формул, для определения скользящих средних Сведение вычисления скользящего среднего к итеративной обработке простых средних, для подсчета которых используются равные веса. Пример: Если взять простое скользящее среднее трех членов, затем построить другое скользящее среднее пяти скользящих средних первого типа, то с множителем 1/15 получим веса: Метод Спенсера определения формулы скользящего среднего для 15 точек: Это среднее, основанное на 15 членах, предполагает четыре последовательных усреднения, три из которых заключаются в вычислении простых арифметических средних. Окончательно веса таковы: 13

Неудобства применения метода скользящих средних 1. Формулы не позволяют вычислить значения тренда для первых и последних m значений ряда; Наличие краевого эффекта. 2. Можно вывести формулу для построения тренда на четном числе точек, однако, при этом значения тренда были бы получены в серединах временных интервалов между наблюдениями. 3. Выделение тренда методом скользящих средних может «исказить» сезонную компоненту 14

Устранение первого недостатка Найдем значения кубического полинома, построенного на семи точках, в моменты t=1, 2, 3, определим значение коэффициентов a 1, a 2, a 3 (из системы (3)) Выражая эти коэффициенты в виде скользящих средних семи последних членов, получаем в очевидных обозначениях, что Например, при t=1, 2, 3 приводится к следующему: 15

Устранение первого недостатка (продолжение) Так если бы последними семью членами ряда были 0, 1, 8, 27, 64, 125, 216, то для третьего от конца члена мы бы получили значение тренда Это значение в точности совпадает с соответствующим членом ряда 16

Устранение второго и третьего недостатка Пример Имеются наблюдения на последний день каждого месяца с января по декабрь. Простое скользящее 12 точек с весами 1/12[12] дает значение тренда в середине июля. Для получения значения тренда на конец июля для сравнения с наблюденными значениями в этой точке, берут арифметическое среднее значение тренда в середине июля и в середине августа. Это эквивалентно вычислению 13 месячного среднего с весами В случае простейших скользящих средних усредненное значение членов находится по формуле: (4) Здесь 2 m – количество точек, на которых строится скользящее среднее. Для устранения третьего недостатка, обычно при построении скользящих средних количество точек сглаживания тренда берут равным периоду сезонности Т. 17

Другие непараметрические методы сглаживания тренда 1. Метод скользящих медиан на т точках сглаживания 2. Метод скользящих экспоненциальных средних (Метод адаптивного сглаживания Брауна) (см. предыдущую лекцию) 18