Метод деревьев в анализе риска Лектор к

«Метод деревьев» в анализе риска Лектор: к. т. н. доц. П. Ф. Агаханянц Группа: 237 Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий

Модификации «метода деревьев» n n n Деревья решений Деревья отказов Деревья событий

Деревья решений n n n Метод позаимствован из теории принятия решений Удобное и наглядное графическое представление ситуации Эффективен, когда сложная проблема может быть разбита на ряд простых задач, решаемых отдельно

Правила построения «деревьев решений» n n n Узлы случаев – не зависят от ЛПР – Узлы решений – зависят от ЛПР – События характеризуются вероятностью и «оценкой» – показателем полезности события Расчет вероятностей проводится слева направо – от прошлого к будущему Расчет оценок проводится справа налево – от будущего к прошлому n n показатель полезности = математическое ожидание показателя при подходе к узлу решений проводится «максимизация» (берется наибольшая оценка)

Задача об инвестициях n У бизнесмена есть $5000 n он может вложить их в покупку товара – d 1 n n n цена товара может подняться +$1000 – a 1 цена товара может опуститься -$1000 – a 2 он может оставить в банке – d 2 p(a 1)=0, 6 p(a 2)=0, 4 События а 1 а 2 d 1 6000 4000 d 1 5000 p(ai) 0, 6 0, 4

Задача об инвестициях n Бизнесмен может обратится к брокеру плата за консультацию – t n брокер может посоветовать: n x 1 – покупать товар n x 2 – не покупать товар n надежность (вероятность правильного совета брокера) в случае подъема цены p(x 1/a 1)=0, 7 n надежность (вероятность правильного совета брокера) в случае падения цены p(x 2/a 2)=0, 65 n

Основные свойства вероятности Суммарная вероятность полной группы событий равна 1 n Вероятности условных событий: p(x 1/a 1)+p(x 2/a 1)=1 p(x 1)=p(x 1/a 1)*p(a 1) + p(x 1/a 2)*p(a 2) n Формула Байеса p(ai/xj)=p(xj/ai)*p(ai)/ p(xj) n

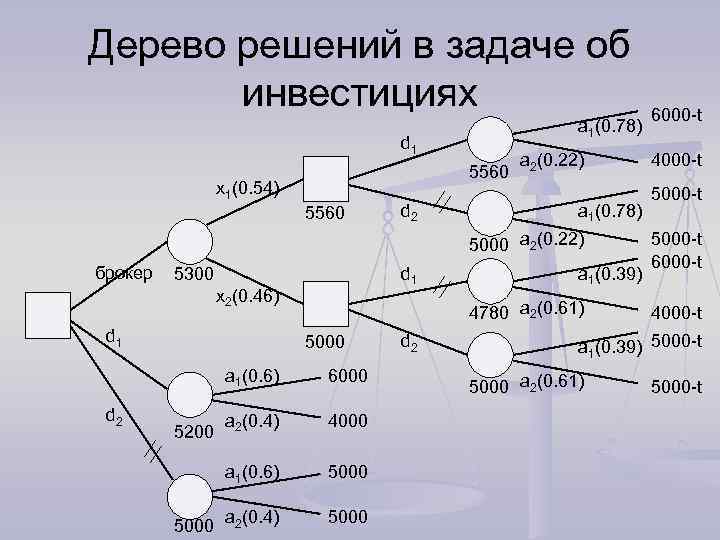Дерево решений в задаче об инвестициях a 1(0. 78) d 1 5560 x 1(0. 54) 5560 d 2 a 2(0. 22) a 1(0. 78) 5000 a 2(0. 22) брокер 5300 d 1 x 2(0. 46) d 1 4780 a 2(0. 61) 5000 a 1(0. 6) d 2 5000 6000 a 2(0. 4) 4000 a 1(0. 6) 5200 a 1(0. 39) 5000 a 2(0. 4) 5000 d 2 6000 -t 4000 -t 5000 -t 6000 -t 4000 -t a 1(0. 39) 5000 -t 5000 a 2(0. 61) 5000 -t

Задача об инвестициях n n n Выбор между величинами 5300 и 5200 зависит от стоимости услуги брокера. Если t<$100, то имеет смысл обращаться к брокеру. $100 – разумный предел дополнительных вложений, обеспечивающий снижение риска с 40% до 22%.

Задача о медицинской операции (качественная оценка последствий) n n n Врач должен решить, делать ли пациенту сложную и опасную операцию пациенту, у которого подозревается опухоль Вероятность правильного диагноза 0, 75 Если опухоль есть и сделать операцию, то вероятность выздоровления 0, 5 Если опухоль есть и не делать операцию, то вероятность выздоровления 0, 05 Если опухоли нет и сделать операцию, то вероятность выздоровления 0, 8 Если опухоли нет и не делать операцию, то вероятность выздоровления 1

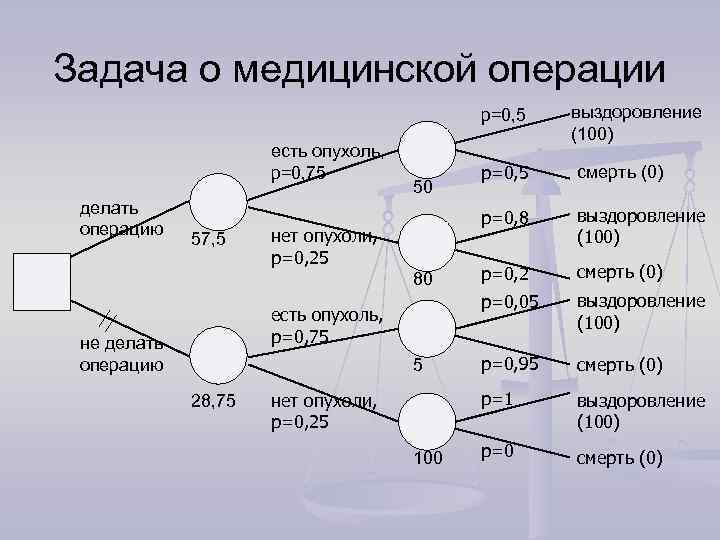Задача о медицинской операции p=0, 5 есть опухоль, p=0, 75 делать операцию 57, 5 5 28, 75 нет опухоли, p=0, 25 100 выздоровление (100) p=0, 2 смерть (0) выздоровление (100) p=0, 95 смерть (0) p=1 есть опухоль, p=0, 75 смерть (0) p=0, 05 нет опухоли, p=0, 25 p=0, 8 50 80 не делать операцию выздоровление (100) p=0 смерть (0)

Задача о медицинской операции n 57, 5 : 28, 75 = 2 – в 2 раза выше шансы выжить при операции, чем в ее отсутствие Задание: Пересчитать задачу об операции, если точность диагноза 100%.