Methoden der Chemie III Teil 1 Modul

Methoden der Chemie III – Teil 1 Modul M. Che. 1101 WS 2010/11 – 1 Moderne Methoden der Anorganischen Chemie Mi 10: 15 -12: 00, Hörsaal II George Sheldrick gsheldr@shelx. uni-ac. gwdg. de

Teil. 1. Kristallstrukturbestimmung Die Vorlesungen werden je ca. 50 Minuten dauern, gefolgt von eine Übung im gleichen Hörsaal (ca. 40 Minuten). Jede Übung wird mit 0 bis 2 Punkten belohnt. Diese Punkte werden 24% der Praktikumsnote ausmachen. Maximal 24 Punkte werden angerechnet (theoretisch wären für die 13 Übungen 26 möglich). Das Praktikum dauert eine Woche (5 Tage, 13 bis 18 Uhr). Es wird in Zweiergruppen gearbeitet und es können maximal 10 Studierende pro Woche das Praktikum absolvieren. Zwei Termine sind im März und vier im Sommersemester vorgesehen. Die Anmeldung erfolgt über Stud-IP. Jede Gruppe fängt montags an und jede/r Studierende wird an dem Freitag seine/ihre Ergebnisse kurz vorstellen und ein paar Fragen dazu beantworten. Die Übungspunkte, die Präsentation und das Praktikumsprotokoll bilden die Grundlage der Benotung. Teil 2 (Meyer/Demeshko, Spektroskopische Methoden) findet Donnerstags 10: 15 -12: 00 statt, gefolgt von einem eigenen Praktikum. Die Klausur (für beide Teile zusammen) findet an Mittwoch, dem 2. März und die Wiederholungsklausur an Mittwoch, dem 6. April 2011 statt.

Warum Kristallstrukturbestimmung? Mit Kernresonanz kann man die ‚Strichformel‘ eines organischen Moleküls bestimmen, aber – ohne Hilfe eines Kraftfeldes – keine Bindungslängen und -winkel bestimmen. Röntgenstrukturbestimmung ist nicht immer die genaueste Methode, Bindungslängen zu bestimmen. Für sehr kleine Moleküle kann die Rotationsspektroskopie oder sogar Elektronenbeugung im Gaszustand genauer sein. Aber die Bestimmung von dreidimensionalen Kristallstrukturen mit Hilfe der Röntgenbeugung ist auch für sehr große Strukturen (Proteine, DNA, Viren. . . ) geeignet, und sehr breit einsetzbar, z. B. für Mineralien, metallorganische Verbindungen oder Naturstoffe. Kristallstrukturen sind sehr objektiv und nach 50 Jahren immer noch gültig. Vor allem anorganische und metallorganische Zeitschriften verlangen Kristallstrukturen als einen Beweis dafür, dass man eine Verbindung tatsächlich synthetisiert hat. Aber: Für die Kristallstrukturbestimmung sind Kristalle unbedingt erforderlich!

Nobelpreise für Kristallographen 1914 M. von Laue 1915 W. H. Bragg und W. L. Bragg 1954 L. Pauling 1962 J. C. Kendrew, M. Perutz, F. Crick, J. D. Watson und M. H. F. Wilkins 1964 Dorothy C. Hodgkin 1976 W. N. Lipscomb 1982 A. Klug 1985 H. A. Hauptman und J. Karle 1988 J. Deisenhofer, R. Huber und H. Michel 1997 J. E. Walker 2003 P. Agre und R. Mac. Kinnon 2006 R. Kornberg 2009 V. Ramakrishnan, T. A. Steiz und Ada Yonath

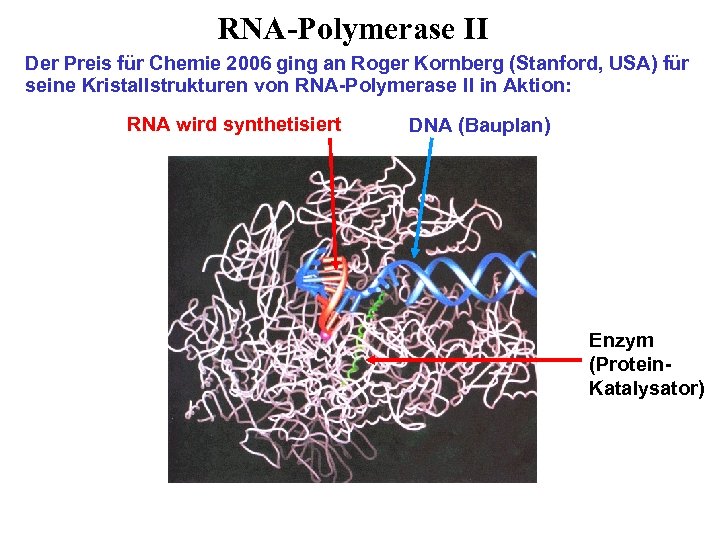RNA-Polymerase II Der Preis für Chemie 2006 ging an Roger Kornberg (Stanford, USA) für seine Kristallstrukturen von RNA-Polymerase II in Aktion: RNA wird synthetisiert DNA (Bauplan) Enzym (Protein. Katalysator)

Das Ribosom Der Preis für Chemie 2009 ging an Venkatraman Ramakrishnan (MRC Cambridge, UK), Thomas A. Steitz (Yale, USA) und Ada Yonath (Weizmann Institut, Israel) für die Aufklärung der Struktur des Ribosoms durch Röntgenbeugung an Kristallen. Kleine Untereinheit: PDB 1 fka, 24982 Atome, Auflösung 3. 3 Å, P 41212, a = b = 496, c = 173 Å. Orange: RNA (ca. 90%), blau: Protein. Große Untereinheit: PDB 1 ffk, 64268 Atome, Auflösung 2. 4 Å, C 2221, a = 212, b = 300, c = 574 Å. RCSB PDB: http: //www. rcsb. org/

Kristallstrukturbestimmung: Literatur Das mit Abstand geeignetste Buch für diesen Kurs ist: W. Massa, Kristallstrukturbestimmung, 6. Auflage Sept. 2009, Teubner Verlag, ISBN 978 -3834806499, ca. 36 Euro. Exemplare dieser Monographie befinden sich in der AC Bibliothek; der Bibliothekar Herr Wöske kann Ihnen helfen, sie zu finden. Biomolecular Crystallography von Bernhard Rupp, 1. Auflage 2010, Garland Science, ISBN 978 -0815340812 (ca. 90 Euro) ist eine umfassende, aktuelle und gut lesbare Beschreibung der Kristallstrukturbestimmung von biologischen Molekülen. Für die ersten zwei Vorlesungen (Punktgruppen) gibt es ein besonders schönes Online-Tutorial: http: //symmetry. otterbein. edu/ Sprechstunde: Dienstags 8: 30 -9: 30 im Zimmer 333 der AC

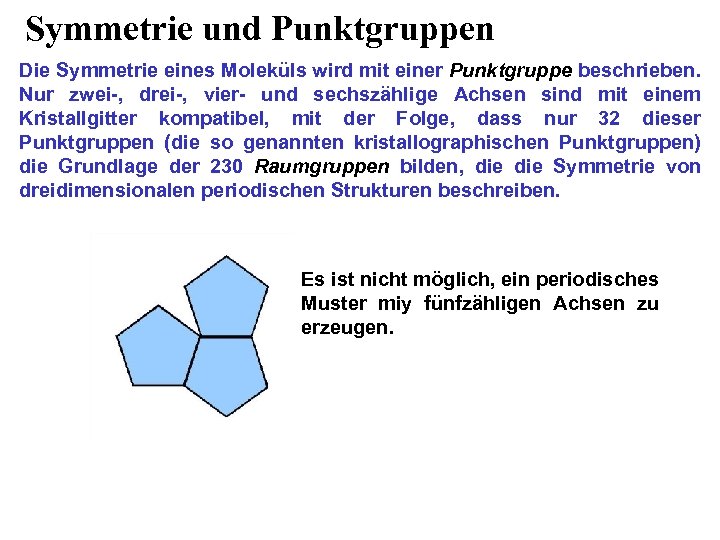Symmetrie und Punktgruppen Die Symmetrie eines Moleküls wird mit einer Punktgruppe beschrieben. Nur zwei-, drei-, vier- und sechszählige Achsen sind mit einem Kristallgitter kompatibel, mit der Folge, dass nur 32 dieser Punktgruppen (die so genannten kristallographischen Punktgruppen) die Grundlage der 230 Raumgruppen bilden, die Symmetrie von dreidimensionalen periodischen Strukturen beschreiben. Es ist nicht möglich, ein periodisches Muster miy fünfzähligen Achsen zu erzeugen.

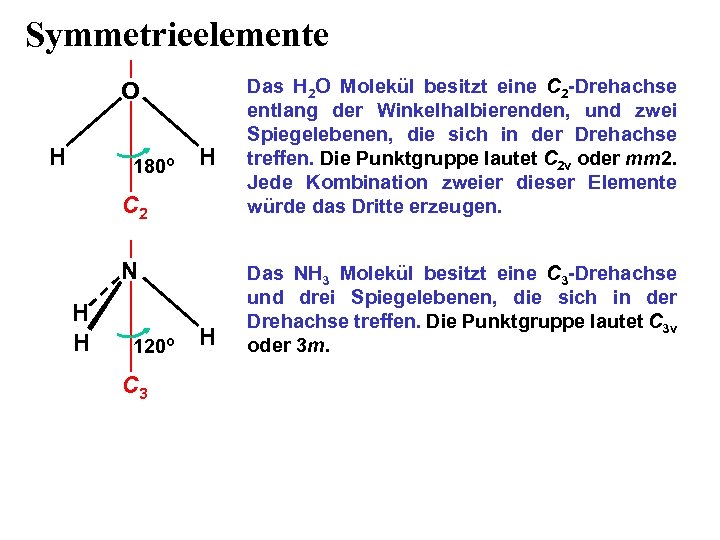Symmetrieelemente O H 180º H C 2 N H H 120º C 3 H Das H 2 O Molekül besitzt eine C 2 -Drehachse entlang der Winkelhalbierenden, und zwei Spiegelebenen, die sich in der Drehachse treffen. Die Punktgruppe lautet C 2 v oder mm 2. Jede Kombination zweier dieser Elemente würde das Dritte erzeugen. Das NH 3 Molekül besitzt eine C 3 -Drehachse und drei Spiegelebenen, die sich in der Drehachse treffen. Die Punktgruppe lautet C 3 v oder 3 m.

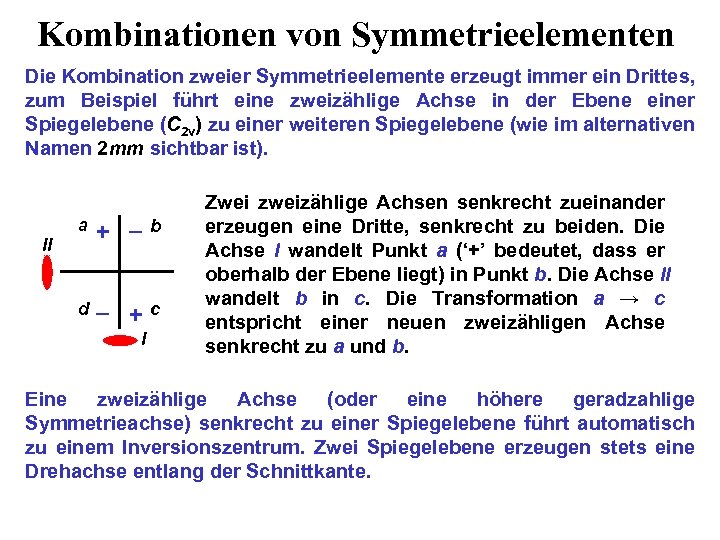Kombinationen von Symmetrieelementen Die Kombination zweier Symmetrieelemente erzeugt immer ein Drittes, zum Beispiel führt eine zweizählige Achse in der Ebene einer Spiegelebene (C 2 v) zu einer weiteren Spiegelebene (wie im alternativen Namen 2 mm sichtbar ist). a + – d – +c II I b Zwei zweizählige Achsen senkrecht zueinander erzeugen eine Dritte, senkrecht zu beiden. Die Achse I wandelt Punkt a (‘+’ bedeutet, dass er oberhalb der Ebene liegt) in Punkt b. Die Achse II wandelt b in c. Die Transformation a → c entspricht einer neuen zweizähligen Achse senkrecht zu a und b. Eine zweizählige Achse (oder eine höhere geradzahlige Symmetrieachse) senkrecht zu einer Spiegelebene führt automatisch zu einem Inversionszentrum. Zwei Spiegelebene erzeugen stets eine Drehachse entlang der Schnittkante.

Schönflies und Hermann-Mauguin Das Schönflies-System wird meist von Spektroskopikern und das Hermann-Mauguin-System von Kristallographen benutzt. Beide Systeme sind etwas gewöhnungsbedürftig. Ein Inversionszentrum heißt ‚i‘ (S) oder ‚ 1‘ (H-M). Bei einer vertikalen Hauptachse heißen vertikale Spiegelebenen ‚v‘ bzw. ‚m‘; horizontale Spiegelebene sind ‚h‘ bzw. ‚/m‘. Eine N-zählige Drehachse heißt CN (S) oder N (H-M). Beispiele: C 1=1; C 2=2; C 3=3; C 4=4; Ci=1; Cs=m; C 2 v=2 mm; C 2 h=2/m [Cs heißt auch C 1 v und 2 mm kann mm 2 genannt werden].

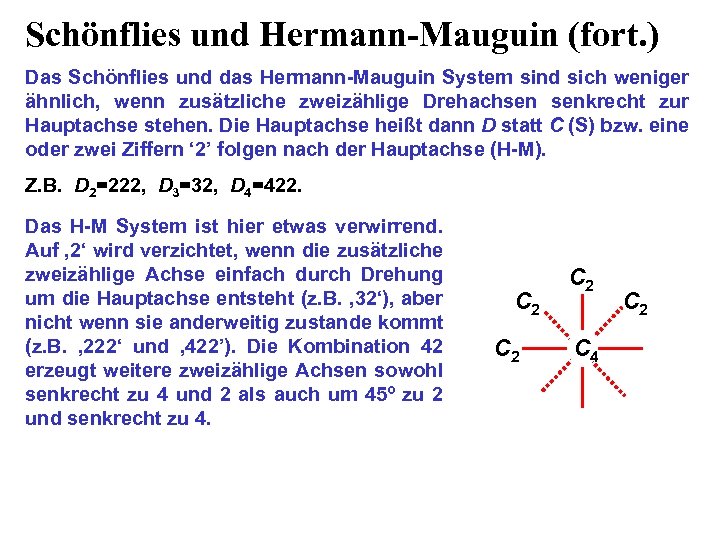Schönflies und Hermann-Mauguin (fort. ) Das Schönflies und das Hermann-Mauguin System sind sich weniger ähnlich, wenn zusätzliche zweizählige Drehachsen senkrecht zur Hauptachse stehen. Die Hauptachse heißt dann D statt C (S) bzw. eine oder zwei Ziffern ‘ 2’ folgen nach der Hauptachse (H-M). Z. B. D 2=222, D 3=32, D 4=422. Das H-M System ist hier etwas verwirrend. Auf ‚ 2‘ wird verzichtet, wenn die zusätzliche zweizählige Achse einfach durch Drehung um die Hauptachse entsteht (z. B. ‚ 32‘), aber nicht wenn sie anderweitig zustande kommt (z. B. ‚ 222‘ und ‚ 422’). Die Kombination 42 erzeugt weitere zweizählige Achsen sowohl senkrecht zu 4 und 2 als auch um 45º zu 2 und senkrecht zu 4. C 2 C 2 C 4 C 2

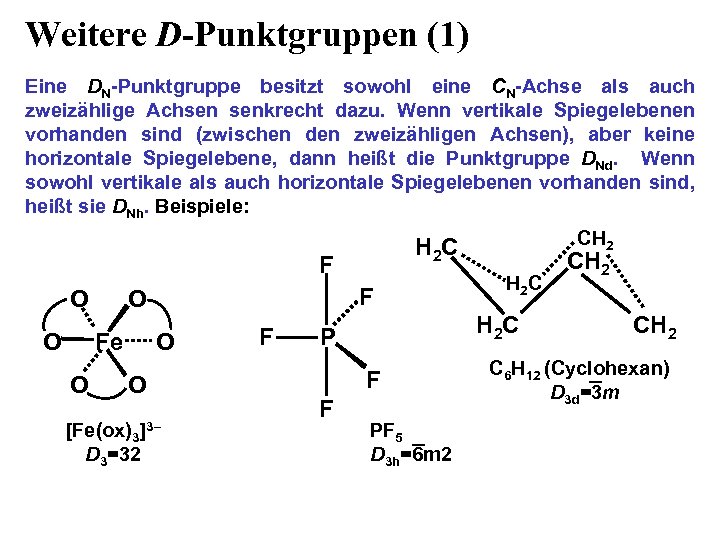Weitere D-Punktgruppen (1) Eine DN-Punktgruppe besitzt sowohl eine CN-Achse als auch zweizählige Achsen senkrecht dazu. Wenn vertikale Spiegelebenen vorhanden sind (zwischen den zweizähligen Achsen), aber keine horizontale Spiegelebene, dann heißt die Punktgruppe DNd. Wenn sowohl vertikale als auch horizontale Spiegelebenen vorhanden sind, heißt sie DNh. Beispiele: F O O Fe O F O O O ]3– [Fe(ox)3 D 3=32 F H 2 C H 2 C P F F CH 2 H 2 C PF 5 D 3 h=6 m 2 CH 2 C 6 H 12 (Cyclohexan) D 3 d=3 m

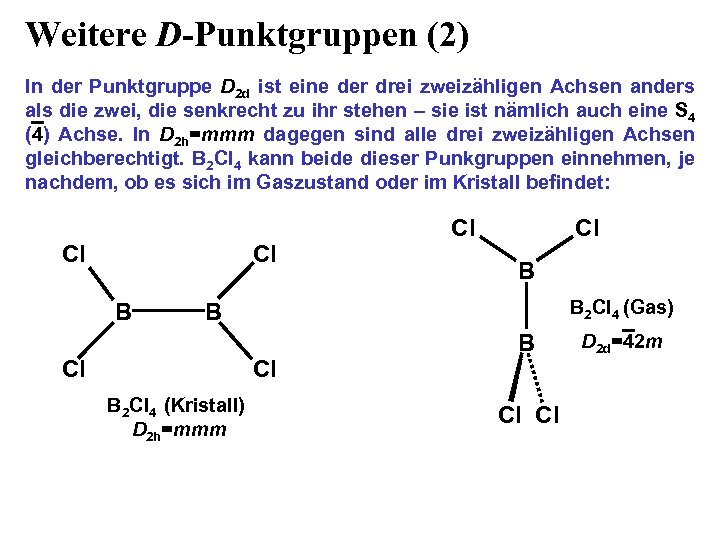Weitere D-Punktgruppen (2) In der Punktgruppe D 2 d ist eine der drei zweizähligen Achsen anders als die zwei, die senkrecht zu ihr stehen – sie ist nämlich auch eine S 4 (4) Achse. In D 2 h=mmm dagegen sind alle drei zweizähligen Achsen gleichberechtigt. B 2 Cl 4 kann beide dieser Punkgruppen einnehmen, je nachdem, ob es sich im Gaszustand oder im Kristall befindet: Cl Cl B B 2 Cl 4 (Gas) B Cl Cl B 2 Cl 4 (Kristall) D 2 h=mmm B Cl Cl D 2 d=42 m

Die 32 kristallographischen Punktgruppen Schönflies Hermann. Mauguin C 1 Ci C 2 Cs=C 1 v C 2 h C 2 v D 2 h C 4 S 4 D 4 C 4 v C 4 h D 2 d D 4 h 1 1 2 m 2/m mm 2 222 mmm 4 4 422 4 mm 4/m 42 m 4/mmm C 3 i=S 6 D 3 C 3 v D 3 d C 6 C 3 h D 6 D 3 h C 6 v D 6 h T Th Td O Oh 3 3 32 3 m 3 m 6 6 622 6 m 2 6/m 6 mm 6/mmm 23 m 3 43 m 432 m 3 m

Übungsfragen Welche Symmetrieelemente und Punktgruppen (nach beiden Systemen) besitzen: 1) H 2 O 2 (gauche) 2) SF 4 3) B 2 H 6 4) C 2 H 6 (gestaffelt und ekliptisch) 5) H 2 C=C=CH 2