Memory effects in electron glasses Markus Müller Eran

Memory effects in electron glasses Markus Müller Eran Lebanon Lev Ioffe Rutgers University, Piscataway NJ ECRYS 2005 Cargèse, 24 August, 2005

Glassiness in electronic systems • Capacitance relaxation in Ga. As, (D. Monroe et al. ) • Slow relaxation, aging, memory in the conductivity of In. Ox (Z. Ovadyahu et al. ) and of granular aluminium (T. Grenet) • Slow relaxation and hysteresis in granular films (A. Goldman et al. , W. Wu et al. ) • Anomalous noise spectra and non-monotonic slow relaxation in Si-MOSFETs close to the 2 D MIT (D. Popović et al. ) • Wigner glass (pinned Wigner crystal) (J. Eisenstein et al. ) • Dielectric glasses (D. Osheroff et al. )

Electron glasses Anderson insulators with strong electron-electron interactions Efros-Shklovskii model M. Pollak (1970) A. Efros, B. Shklovskii (1975) J. H. Davies, P. A. Lee, T. M. Rice (1982, 84) C. Yu, T. Vojta, M. Schreiber, A. Möbius etc. Occupation of sites on a given lattice Unscreened Coulomb interactions Disorder Background charge/gate voltage

Electron glasses Anderson insulators with strong electron-electron interactions Efros-Shklovskii model M. Pollak (1970) A. Efros, B. Shklovskii (1975) J. H. Davies, P. A. Lee, T. M. Rice (1982, 84) C. Yu, T. Vojta, M. Schreiber, A. Möbius etc. Occupation of sites on a given lattice Unscreened Coulomb interactions Disorder Background charge/gate voltage Strongly localized electrons → Classical problem with strong frustration Long range antiferromagnetic spin glass

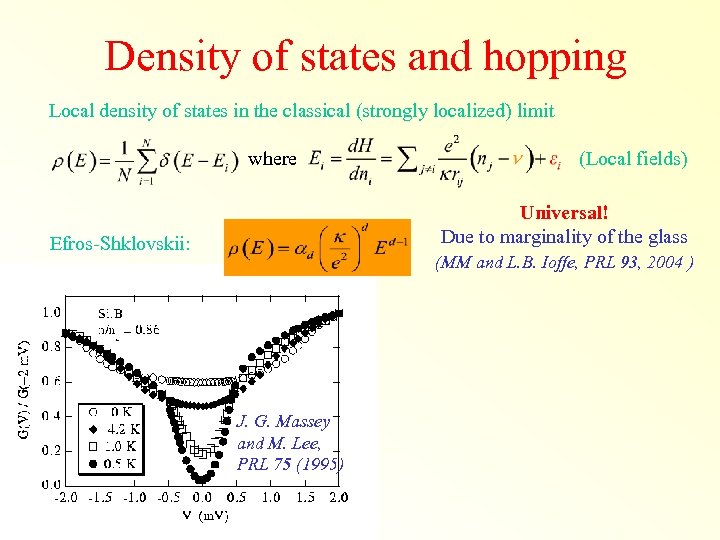Density of states and hopping Local density of states in the classical (strongly localized) limit where (Local fields) Universal! Due to marginality of the glass Efros-Shklovskii: (MM and L. B. Ioffe, PRL 93, 2004 ) J. G. Massey and M. Lee, PRL 75 (1995)

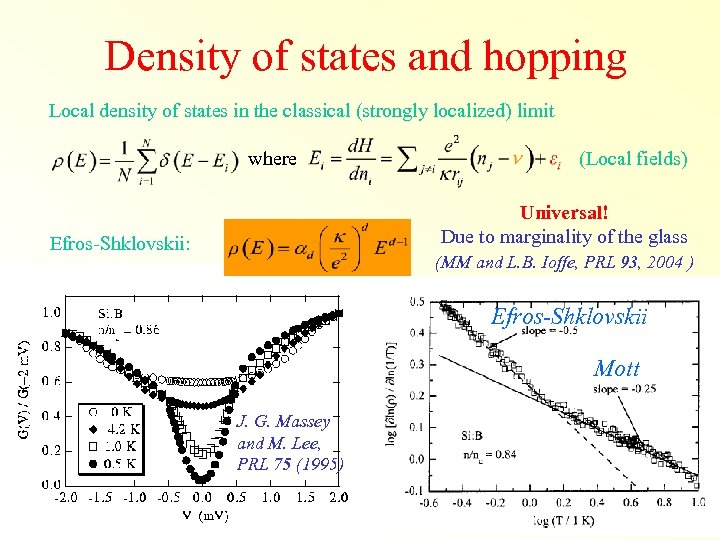Density of states and hopping Local density of states in the classical (strongly localized) limit where (Local fields) Universal! Due to marginality of the glass Efros-Shklovskii: (MM and L. B. Ioffe, PRL 93, 2004 ) Efros-Shklovskii Mott J. G. Massey and M. Lee, PRL 75 (1995)

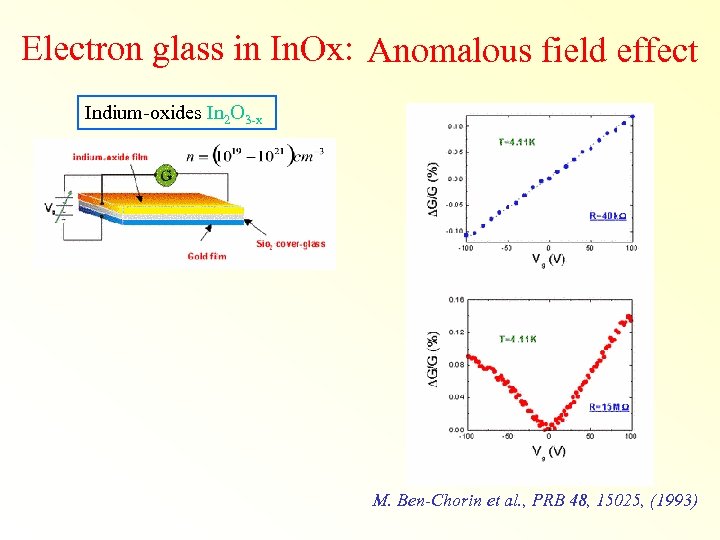Electron glass in In. Ox: Anomalous field effect Indium-oxides In 2 O 3 -x M. Ben-Chorin et al. , PRB 48, 15025, (1993)

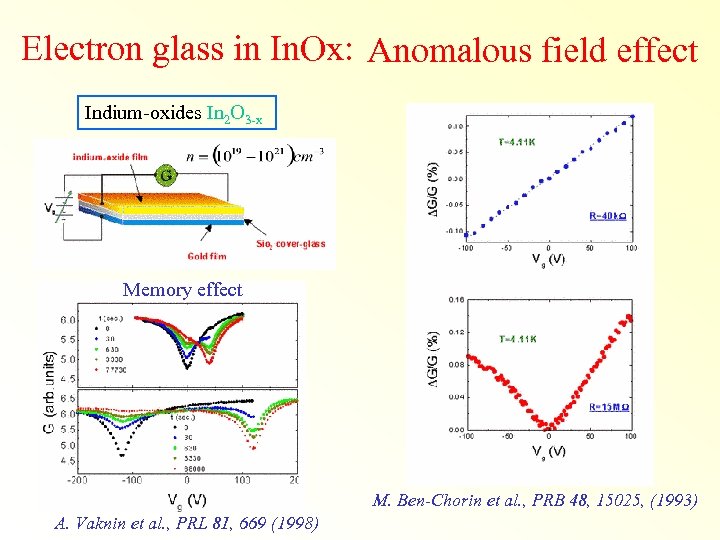Electron glass in In. Ox: Anomalous field effect Indium-oxides In 2 O 3 -x Memory effect M. Ben-Chorin et al. , PRB 48, 15025, (1993) A. Vaknin et al. , PRL 81, 669 (1998)

Properties of the memory cusp Z. Ovadyahu, Phil. Mag. B 81, 1225 (2001) The normalized shape of the anomalous field effect • is independent of disorder strength and magnetic field (localisation length)!

Properties of the memory cusp Z. Ovadyahu, Phil. Mag. B 81, 1225 (2001) The normalized shape of the anomalous field effect • is independent of disorder strength and magnetic field (localisation length)! • widens with increasing carrier density (evidence for Coulomb interaction!)

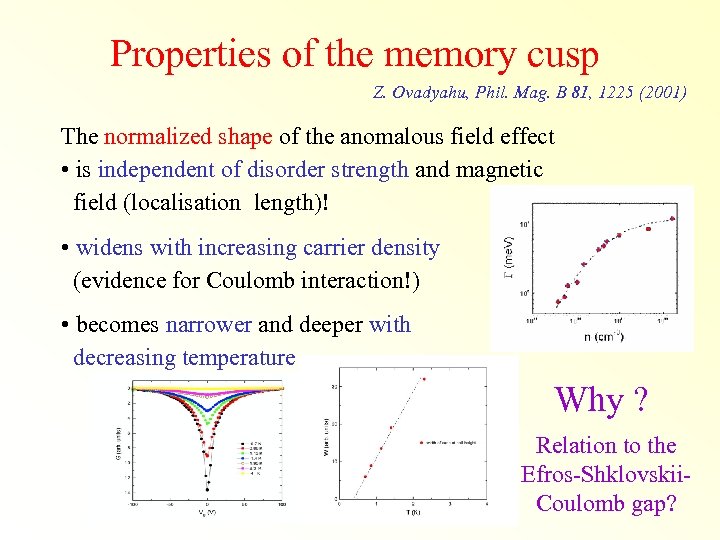Properties of the memory cusp Z. Ovadyahu, Phil. Mag. B 81, 1225 (2001) The normalized shape of the anomalous field effect • is independent of disorder strength and magnetic field (localisation length)! • widens with increasing carrier density (evidence for Coulomb interaction!) • becomes narrower and deeper with decreasing temperature Why ? Relation to the Efros-Shklovskii. Coulomb gap?

Questions • Relation between Coulomb gap and glassiness? • Relation between conductivity cusp and Coulomb gap? • Quantitative theory of the anomalous field effect?

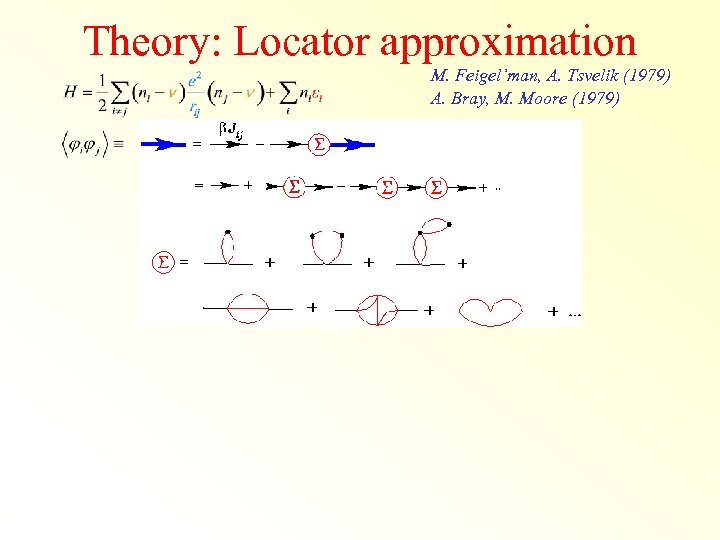Theory: Locator approximation M. Feigel’man, A. Tsvelik (1979) A. Bray, M. Moore (1979)

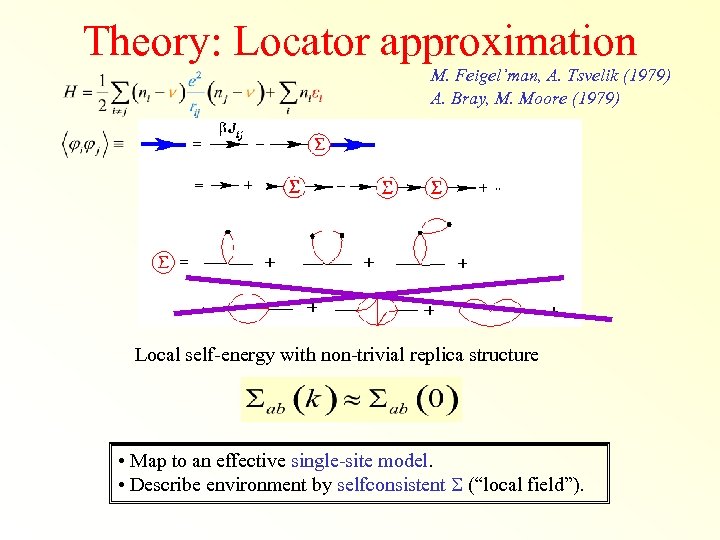Theory: Locator approximation M. Feigel’man, A. Tsvelik (1979) A. Bray, M. Moore (1979) Local self-energy with non-trivial replica structure • Map to an effective single-site model. • Describe environment by selfconsistent S (“local field”).

Results MM and L. Ioffe (PRL 2004) • Prediction of a glass transition at finite temperature (for strong disorder in the universality class of the SK spin glass) 3 D 2 D • Below Tc : Glass state is marginally stable (full RSB!) → Soft modes, slow non-exponential relaxation → Saturation (universality) of the Efros-Shklovskii Coulomb gap in the local density of states

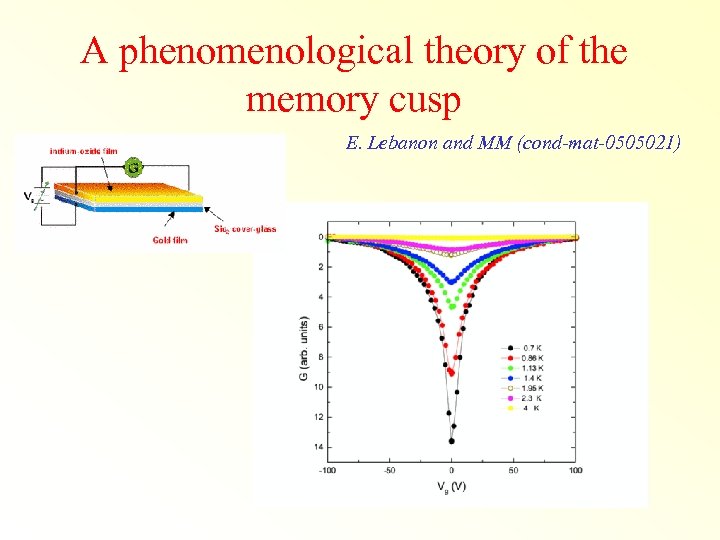A phenomenological theory of the memory cusp E. Lebanon and MM (cond-mat-0505021)

Density of states out of equilibrium T=0 V=0 2 D Density of states

Density of states out of equilibrium T=0 V=0 T finite V = 0 2 D Density of states

Density of states out of equilibrium T=0 V=0 T finite V = 0 T finite V finite 2 D Density of states

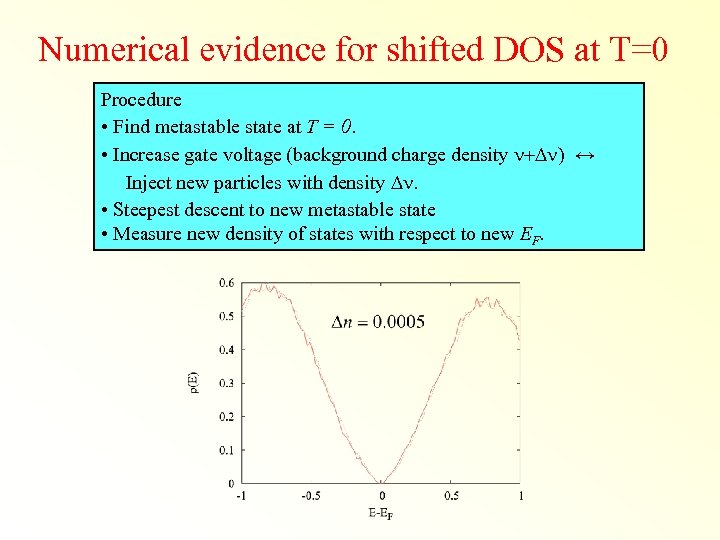Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

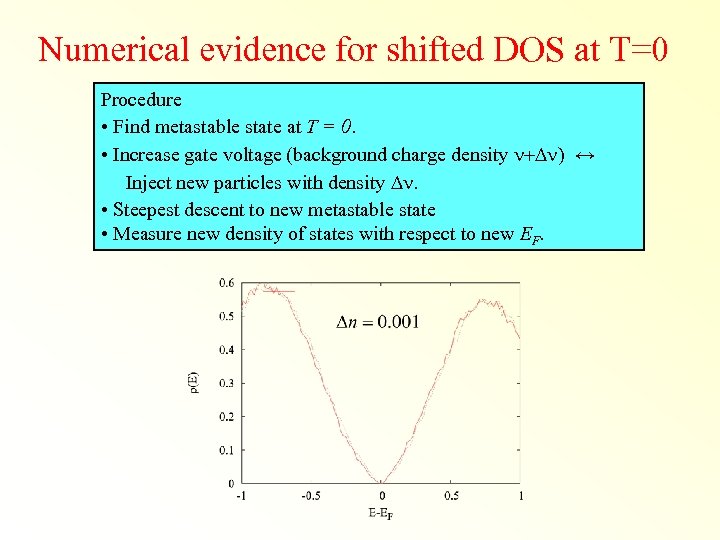Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

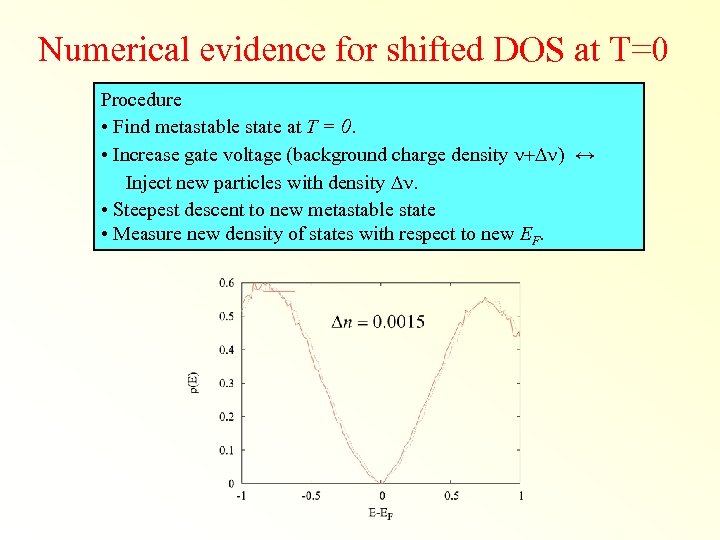Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

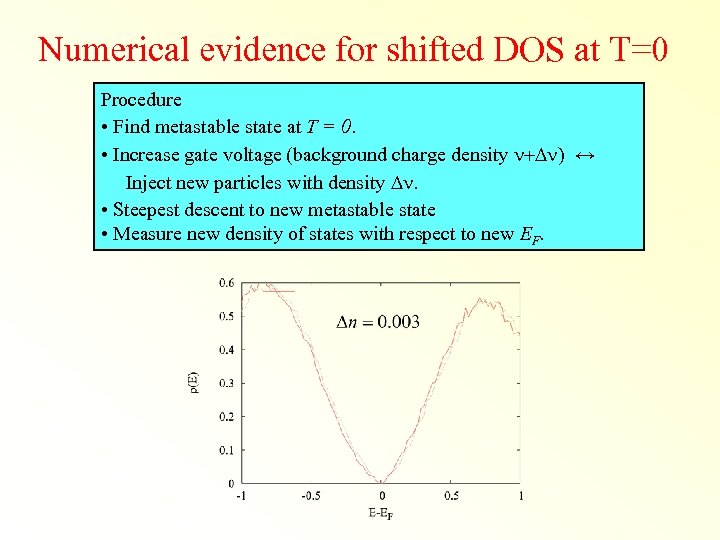Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

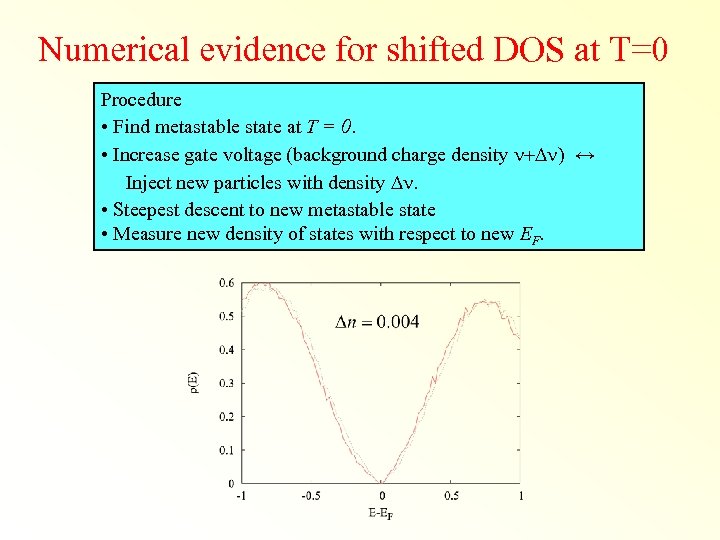Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

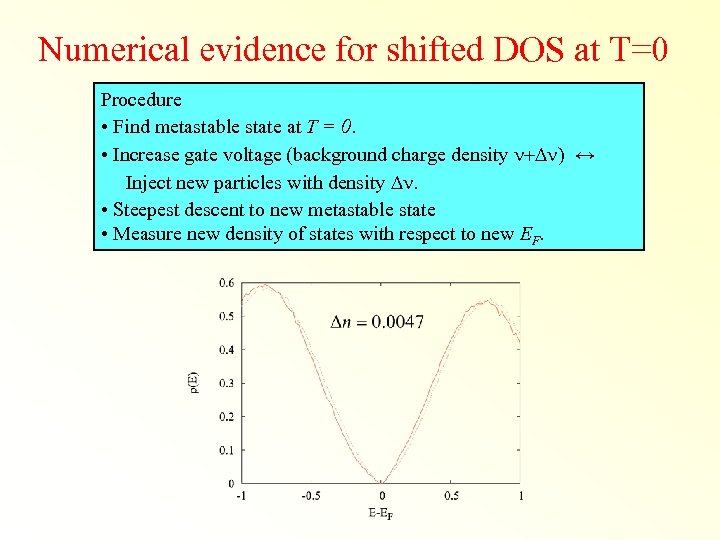Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

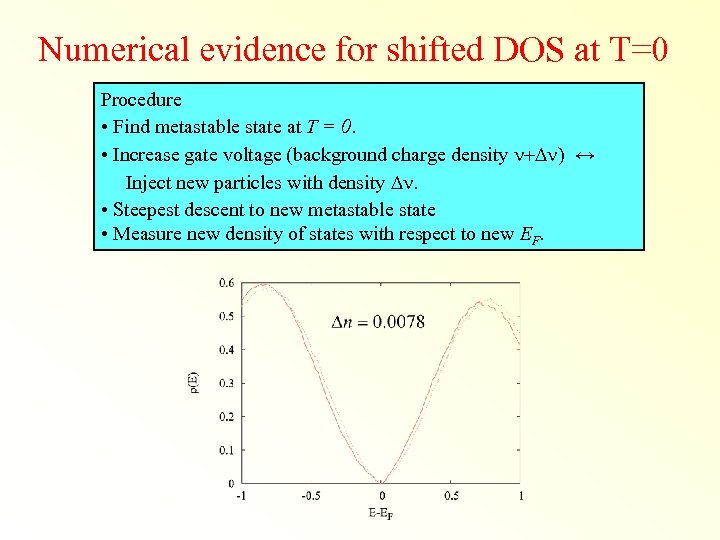Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

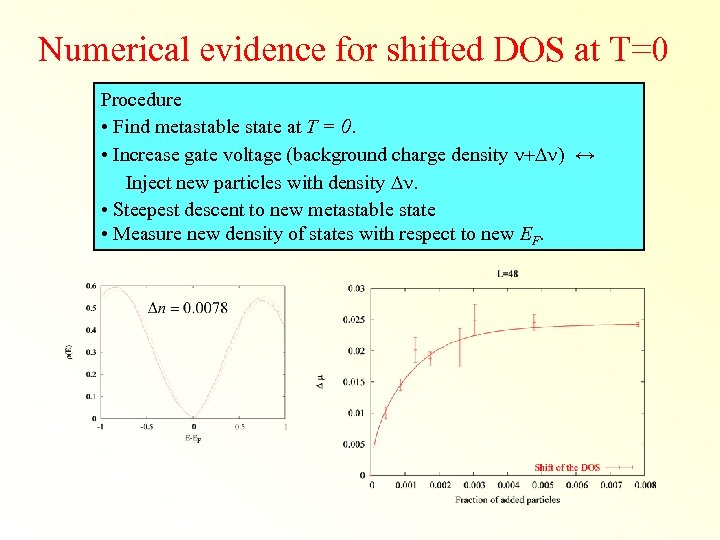Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF.

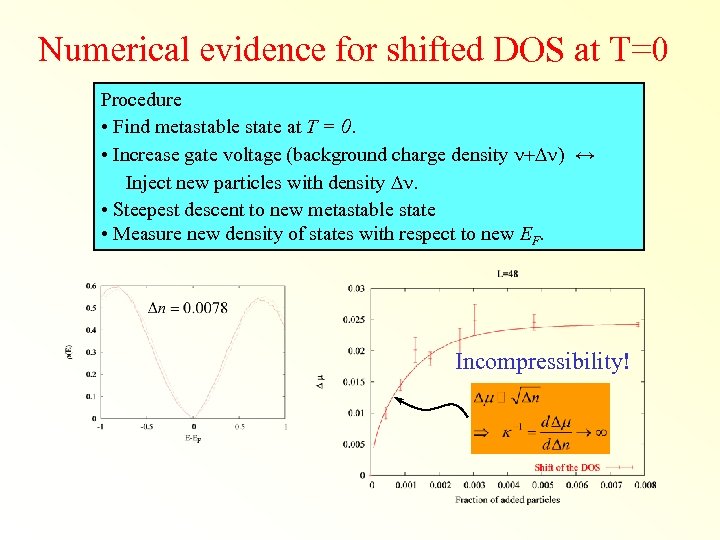Numerical evidence for shifted DOS at T=0 Procedure • Find metastable state at T = 0. • Increase gate voltage (background charge density n+Dn) ↔ Inject new particles with density Dn. • Steepest descent to new metastable state • Measure new density of states with respect to new EF. Incompressibility!

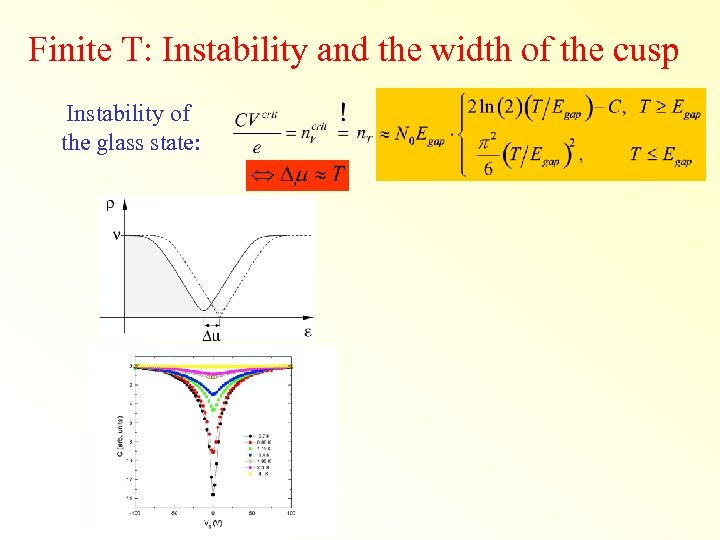Finite T: Instability and the width of the cusp Instability of the glass state:

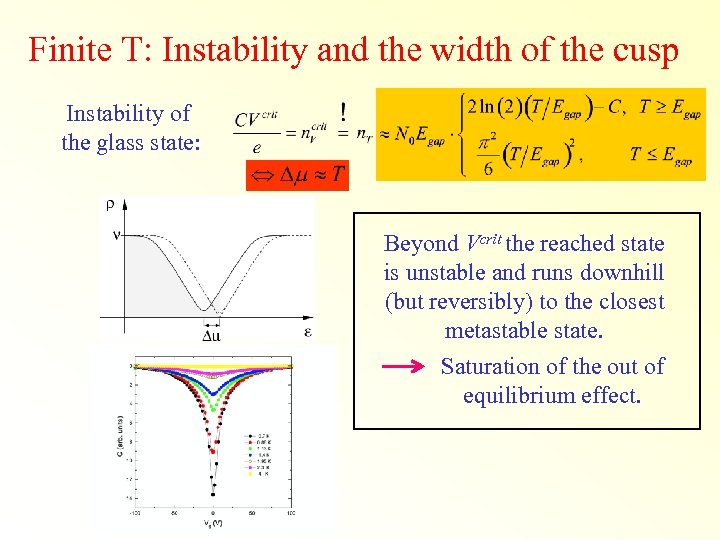Finite T: Instability and the width of the cusp Instability of the glass state: Beyond Vcrit the reached state is unstable and runs downhill (but reversibly) to the closest metastable state. Saturation of the out of equilibrium effect.

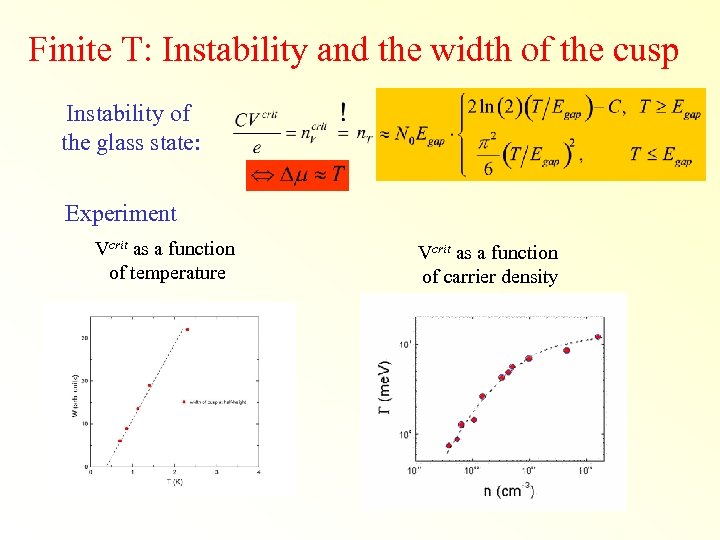Finite T: Instability and the width of the cusp Instability of the glass state: Experiment Vcrit as a function of temperature Vcrit as a function of carrier density

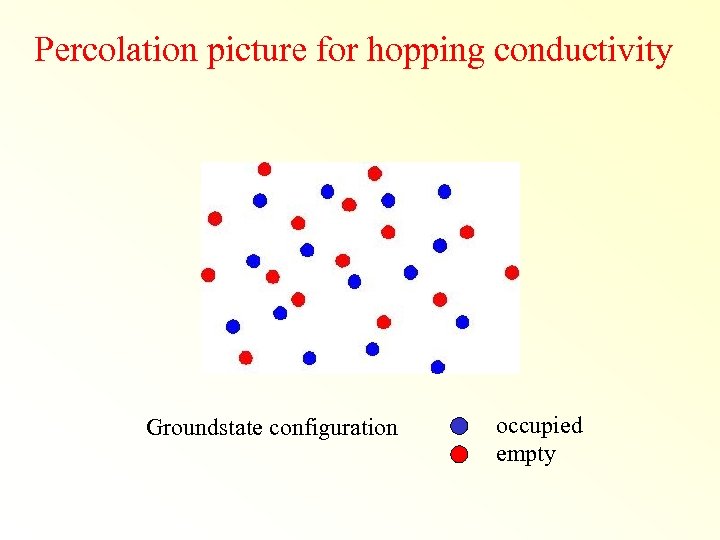Percolation picture for hopping conductivity Groundstate configuration occupied empty

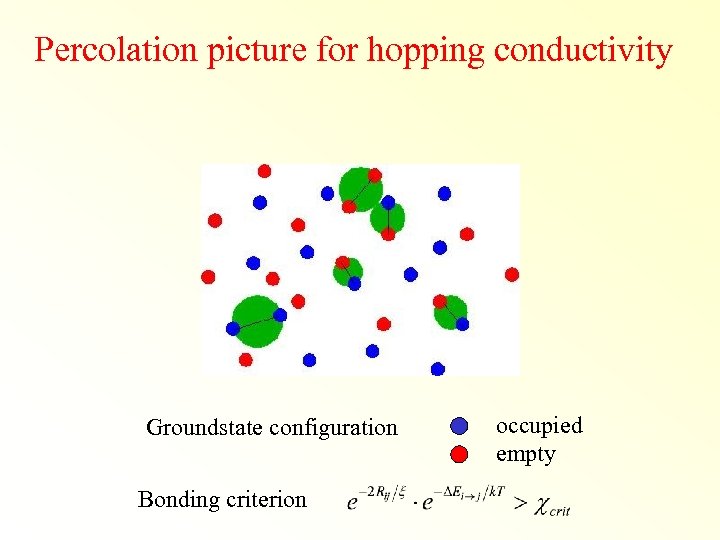Percolation picture for hopping conductivity Groundstate configuration Bonding criterion occupied empty

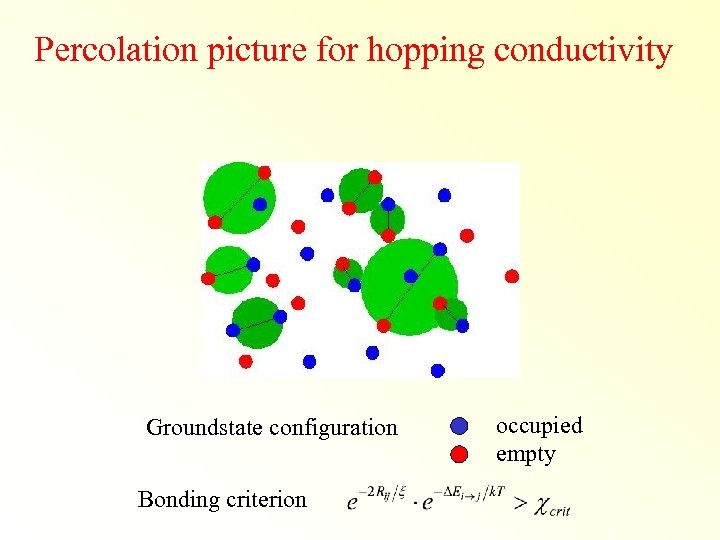Percolation picture for hopping conductivity Groundstate configuration Bonding criterion occupied empty

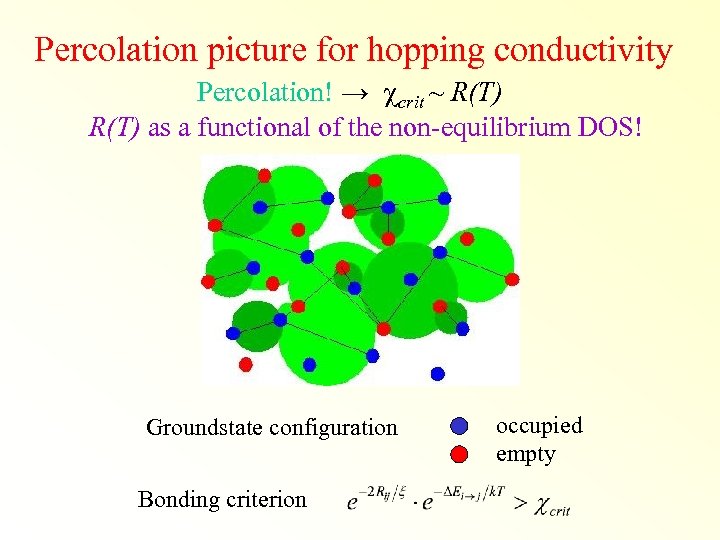Percolation picture for hopping conductivity Percolation! → crit ~ R(T) as a functional of the non-equilibrium DOS! Groundstate configuration Bonding criterion occupied empty

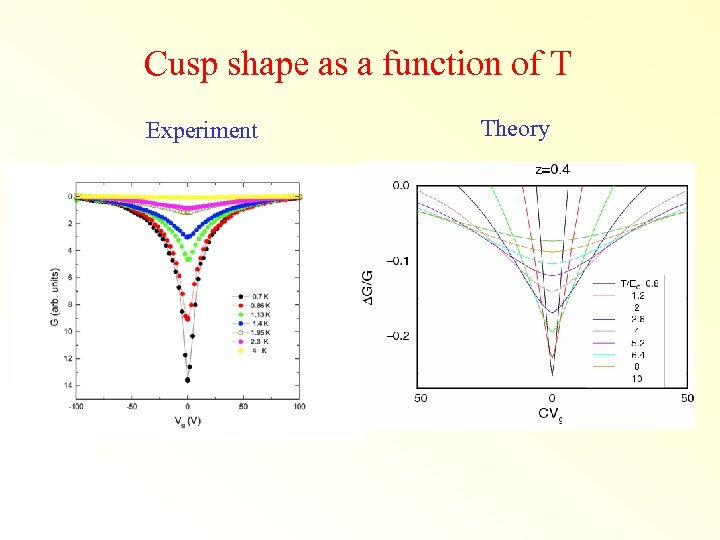Cusp shape as a function of T Experiment Theory

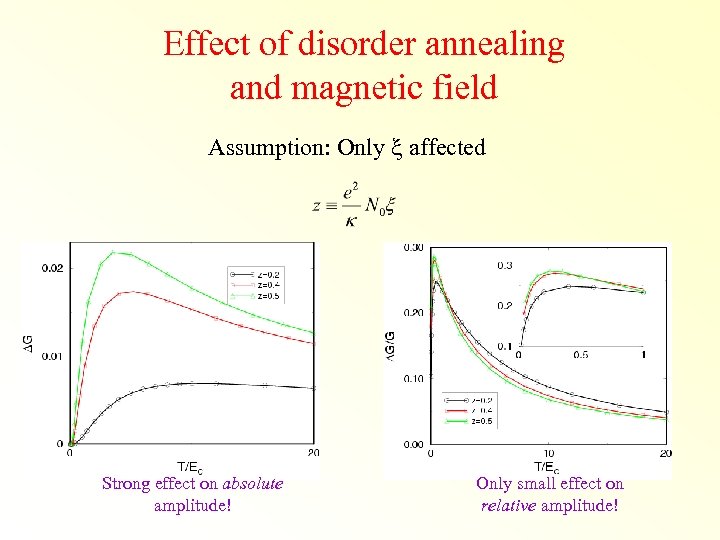Effect of disorder annealing and magnetic field Assumption: Only x affected Strong effect on absolute amplitude! Only small effect on relative amplitude!

Summary Mean field theory for the classical electron glass: • Glass transition at finite T • Marginal stability of the glass (with full RSB) explains • the presence of soft modes • the universality of the Coulomb gap Phenomenological theory for the anomalous field effect (memory cusp): • The conductivity dip results from the rigidity of the glass against collective rearrangements. → Asymmetry in the local density of states → Enhanced hopping