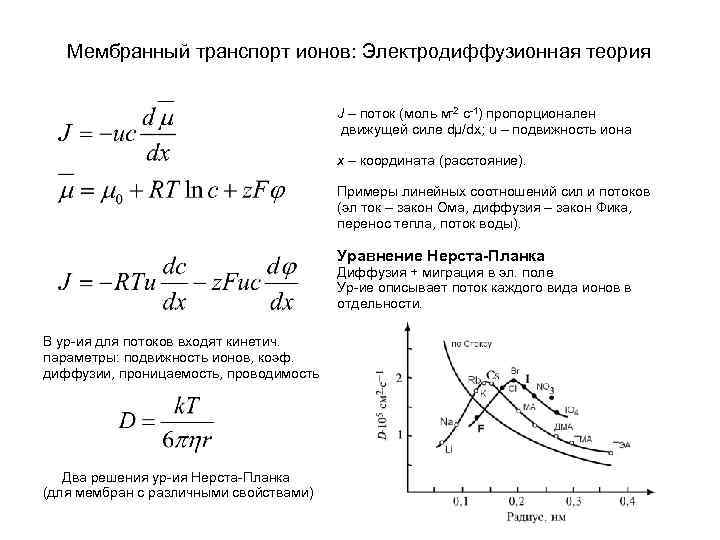
Мембранный транспорт ионов: Электродиффузионная теория J – поток (моль м-2 с-1) пропорционален движущей силе dμ/dx; u – подвижность иона x – координата (расстояние). Примеры линейных соотношений сил и потоков (эл ток – закон Ома, диффузия – закон Фика, перенос тепла, поток воды). Уравнение Нерста-Планка Диффузия + миграция в эл. поле Ур-ие описывает поток каждого вида ионов в отдельности. В ур-ия для потоков входят кинетич. параметры: подвижность ионов, коэф. диффузии, проницаемость, проводимость Два решения ур-ия Нерста-Планка (для мембран с различными свойствами)
(1) Неселективная мембрана (крупнопористые фильтры) Диф. потенциал возникает на кончике стеклянных микропипеток, в электродах сравнения и пр. Конц-ии c+ и c− совпадают при любом x: J+ = J−, c+ = c−= c В этом случае соблюдается условие электронейтральности по всей мембране, т. е. Упражнение: На основе ур-ия Нернста-Планка вывести формулу (Планка-Гендерсона) для диф. потенциала: Упражнение: Определить величину и полярность Δφ на торце пипетки при её заполнении 1 М раствором Na. Cl и погружении в 1 м. М раствор Na. Cl. Подвижность u. Na = 5. 2· 10 -8 м 2 с-1·В-1, u. Cl = 7. 9 10 -8 м 2 с-1·В-1. Для грубой оценки можно принять u. Cl ≈ 1. 5 u. Na 2
(2) Теория постоянного эл. поля Для липидных мембран условие электронейтральности мембраны не выполняется, т. к. С+ ≠ С- (см. «равновесие на границе масло-вода» ) Исходные постулаты: - Мембрана - однородная сплошная среда, где происходят диффузия и миграция ионов; - При отсутствии трансмембранной разности эл потенциалов (РЭП) эл. поля в мембране нет, а при наличии РЭП эл поле в мембране меняется линейно. - Ионы движутся в мембране независимо друг от друга, не взаимодействуя между собой - Конц-ии ионов на двух сторонах внутри мембраны пропорциональны конц-ям в каждом из контактирующих растворов с коэф-том пропорциональности γ ( γ –коэф. распределения). Исходно Т. к. эл потенциал меняется в мембране линейно, то φ=φm h мембранный потенциал толщина мембраны Ур-ие Нернста-Планка сводится к линейному диф. уравнению с одной переменной – с (а не с двумя переменными - c и φ). 3
Конц-ии с в этом ур -ии – в пределах мембраны. При интегрировании dc/dx от x=0 до x=h получим конц-ии на краях внутри мембраны. Можно перейти к конц-иям в водных р-рах с учетом коэф-та γ. Получим (без вывода): Ур-ие Гольдмана-Ходжкина. Каца для ионного тока где P – проницаемость γ – коэф. распределения «мембрана – вода» С учетом размерности входящих величин – u [м 2 с-1 В-1] P = u. RTγ/(z. Fh) u. RT/(z. F)=D P=Dγ/h 4
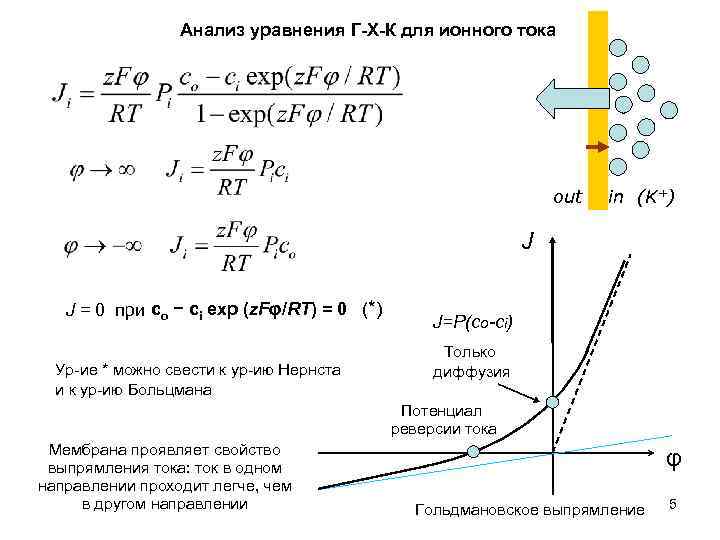
Анализ уравнения Г-Х-К для ионного тока out in (K+) J J = 0 при co − ci exp (z. Fφ/RT) = 0 (*) Ур-ие * можно свести к ур-ию Нернста и к ур-ию Больцмана J=P(co-ci) Только диффузия Потенциал реверсии тока Мембрана проявляет свойство выпрямления тока: ток в одном направлении проходит легче, чем в другом направлении φ Гольдмановское выпрямление 5
Ионная проводимость мембраны Частный случай: сo = сi ; Ур-ие Г-Х-К упрощается (прямая зависимость тока от потенциала) Поток в-ва в молях. Эл. ток (перенос зарядов) Проводимость. Размерность: Ом− 1 = Сименс (См) Упражнение: Найти диапазон изменений проводимости при варьировании РЭП на мембране. Упражнение: рассчитать проводимость K-селективной мембраны (PK=4 10 -10 м/с), омываемой 0. 1 М раствором KCl.
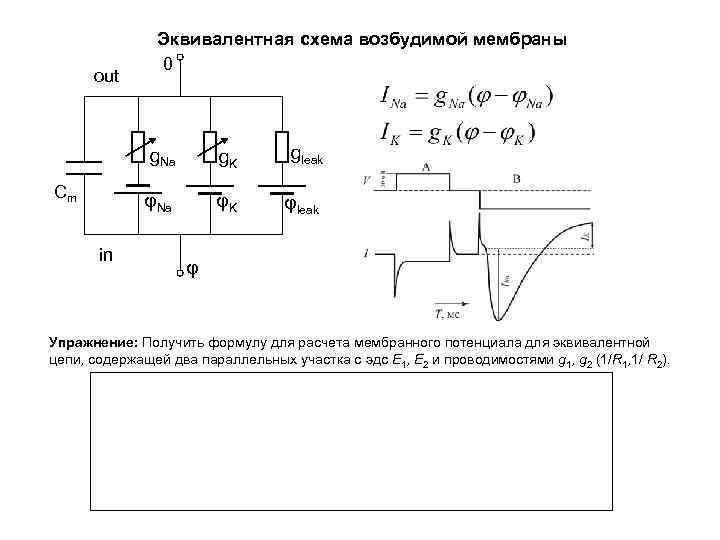
out Эквивалентная схема возбудимой мембраны 0 g. Na in gleak φNa Сm g. K φK φleak φ Упражнение: Получить формулу для расчета мембранного потенциала для эквивалентной цепи, содержащей два параллельных участка с эдс Е 1, Е 2 и проводимостями g 1, g 2 (1/R 1, 1/ R 2).
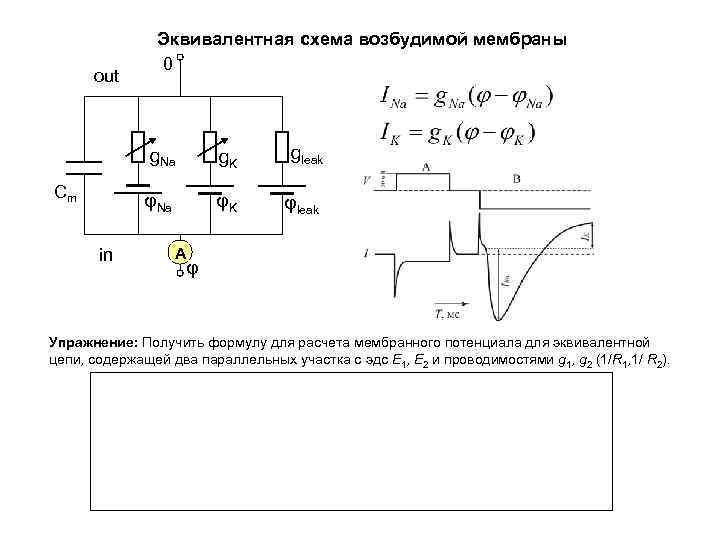
out Эквивалентная схема возбудимой мембраны 0 g. Na in gleak φNa Сm g. K φK φleak A φ Упражнение: Получить формулу для расчета мембранного потенциала для эквивалентной цепи, содержащей два параллельных участка с эдс Е 1, Е 2 и проводимостями g 1, g 2 (1/R 1, 1/ R 2).
out Эквивалентная схема возбудимой мембраны 0 g. Na Сm g. K φNa in φK gleak φ Упражнение: Получить формулу для расчета мембранного потенциала для эквивалентной цепи, содержащей два параллельных участка с эдс Е 1, Е 2 и проводимостями g 1, g 2 (1/R 1, 1/ R 2).
Соотношение Уссинга Суммарный поток равен разности односторонних потоков Выявление потоков, обусловленных только градиентами эл потенциала и концентрации (при отсутствии взаимодействия). φ0 – равновесный потенциал, φ– мембранный потенциал. 10
Скачать презентацию Мембранный транспорт ионов Электродиффузионная теория J поток
Lect 5a.ppt