Membership Control in P 2 P and MANETs

Membership Control in P 2 P and MANETs Nitesh Saxena, Gene Tsudik, Jeong H. Yi Computer Science Department University of California at Irvine {nitesh, gts, jhyi}@ics. uci. edu 1

Outline l Introduction and Motivation l Admission Control l Distributed Cryptography l System Design and Integration l Performance Evaluation l Conclusion 2

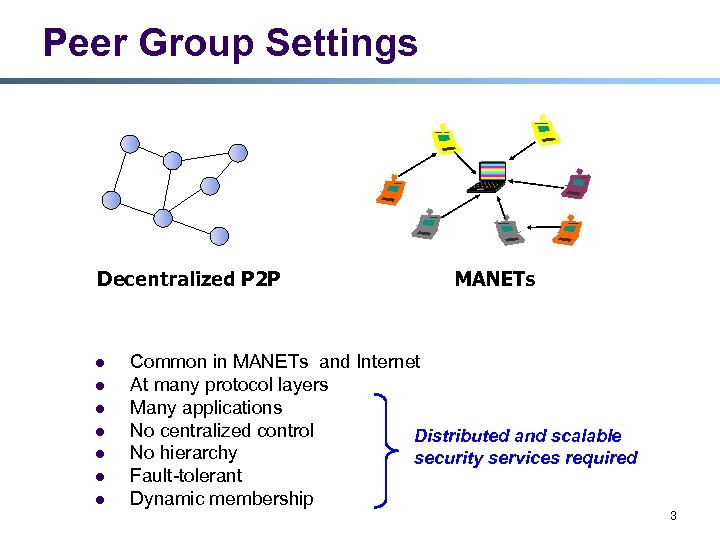
Peer Group Settings Decentralized P 2 P l l l l MANETs Common in MANETs and Internet At many protocol layers Many applications No centralized control Distributed and scalable No hierarchy security services required Fault-tolerant Dynamic membership 3

P 2 P Security: Prior Work Secure communication: l Key management l Authentication l Anonymity l Secure routing 4

Key Management E D F C A B 5

Sybil attack l l Douceur [IPTPS’ 02] An adversary may create multiple identities G I J D B A 3 C H E A 2 A 1 F Lesson: Verify identities 6

Motivation l l Secure group communication does not address membership eligibility Without secure admission control, secure communication (e. g. , key management) is useless 7

Outline l Introduction and Motivation l Admission Control l Distributed Cryptography l System Design and Integration l Performance Evaluation l Conclusion 8

Group Membership Issues l l Naming: l Name ownership? Location? Presence: l on-line: e. g. , replicated servers, MANETs l off-line: e. g. , Gnutella, MANETs Membership: l Static, ad hoc: reflected where? l Enumerated l Dynamic: admission rules/policies? Longevity: l Long-term l Transient 9

What does a prospective member know? l l l Group name, at least… Group location? Group membership? Group charter/policy? Group member(s)’ name(s)/address(es)? 10

Terminology l Group Charter l l Group Membership Certificate (GMC) l l defines admission policies Threshold Sig. Algo Dealer etc. proves membership Group Authority (GAUTH) l Bootstrapping entity 11

Admission Control Models l Admission via Public ACL l l Not suitable for dynamic peer groups Admission by Centralized Authority l l l Not suitable for dynamic peer groups Single point of failure Admission by Members our focus 12

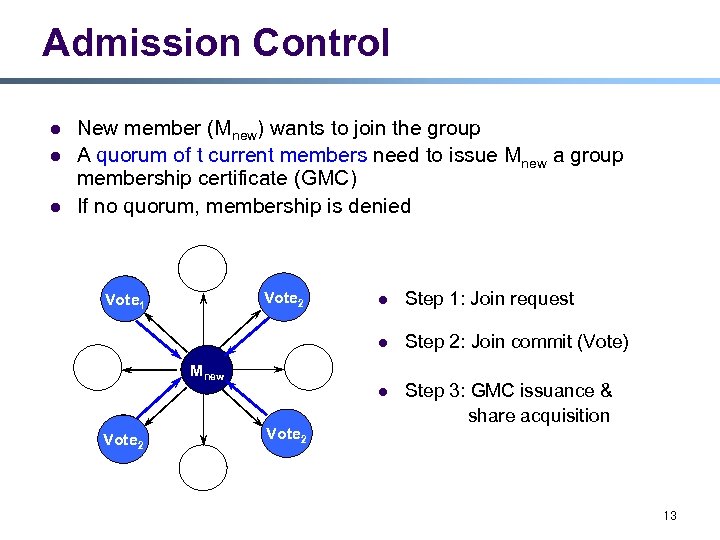
Admission Control l New member (Mnew) wants to join the group A quorum of t current members need to issue Mnew a group membership certificate (GMC) If no quorum, membership is denied l Step 1: Join request l Step 2: Join commit (Vote) l Vote 2 Vote 1 Step 3: GMC issuance & share acquisition Mnew Vote 2 13

Threshold Types l Fixed Threshold l l l Expressed as minimum # of votes (e. g. , 5) What if group size < threshold? Dynamic Threshold l l l Expressed as percentage of # of current members (e. g. , 30%) Threshold = percentage * group size Need to keep accurate state of up-to-date group size Ø Group Authority (GAUTH), as bootstrapping node, is only trusted to keep account of group size. 14

Relevant crypto techniques l l Plain signatures ASMs Aggregated Signatures Threshold Signatures l l l Static Dynamic Group signatures 15

Plain Signatures l l l l l Inefficient in bw/space Efficient in generation/verification Can be gathered asynchronously Can be used to prove membership No membership awareness Accountability Limited anonymity Linkable Lineage problem! 16

Accountable sub-Group Multi-Signatures l l l l l Due to Ohta, et al. (CCS’ 01) Based on aggregating Schnorr signatures Efficient (but still linear in size) Synchronous (on-line protocol) Membership awareness Can be used to prove membership Accountability Limited anonymity Linkable Lineage Problem! 17

Threshold Signatures l l l Desmedt/Frankel (1989) and many others Usually fixed t Function sharing to avoid reconstruction Inefficient Synchronous (on-line protocol) Membership awareness (partial) No Accountability Limited anonymity Linkable? (Usually) need trusted dealer to set up No lineage problem! 18

Dynamic Threshold Signatures l l l l l Frankel, et al. (FOCS’ 97) Shrinkable t Very inefficient Synchronous (on-line protocol) Membership awareness (partial) No Accountability Limited anonymity Linkable? Still need trusted dealer 19

Dynamic Threshold Signatures l l l l l Kong, et al. (ICNP’ 01) Supports growing t Efficiency unclear Synchronous (on-line protocol) Membership awareness (partial) No Accountability Limited anonymity Linkable? Still need trusted dealer to set up 20

Group Signatures l l l l Chaum & Van Heijst (1991) and many others Inefficient Asynchronous No membership awareness Can be used to prove membership Accountability (off-line, by Gr. Mgr) Anonymity Unlinkable (except by Gr. Mgr) 21

Outline l Introduction and Motivation l Admission Control l Distributed Cryptography l System Design and Integration l Performance Evaluation l Conclusion 22

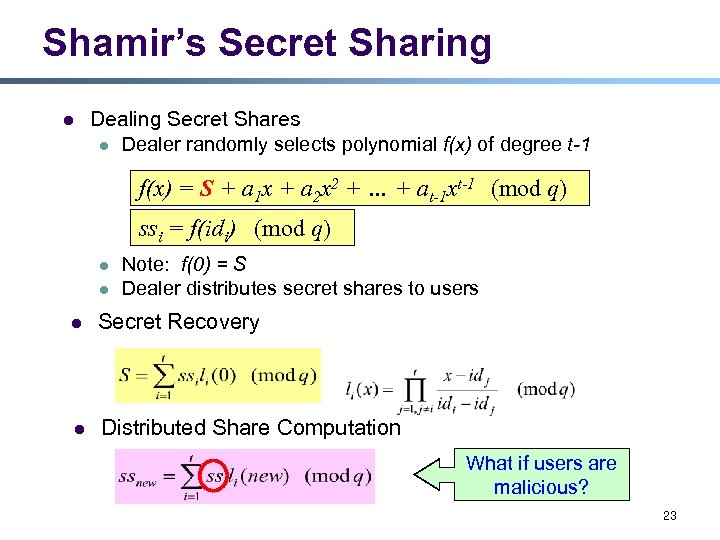
Shamir’s Secret Sharing l Dealing Secret Shares l Dealer randomly selects polynomial f(x) of degree t-1 f(x) = S + a 1 x + a 2 x 2 + … + at-1 xt-1 (mod q) ssi = f(idi) (mod q) l l Note: f(0) = S Dealer distributes secret shares to users l Secret Recovery l Distributed Share Computation What if users are malicious? 23

Verifiable Secret Sharing (VSS) l l P. Feldman [FOCS’ 87] Select f(x) over Zq as in Shamir’s f(x) = a 0 + a 1 x + a 2 x 2 + … + at-1 xt-1 (mod q) l Setup - Exponent is in mod q - q, p : large prime Witness generation (publicly known) - q a p-1 Wi = g| (mod q) (mod p) l l l p, q (q divides p-1) b Zp * , i l Secret share verification (mod q) (mod p) 24

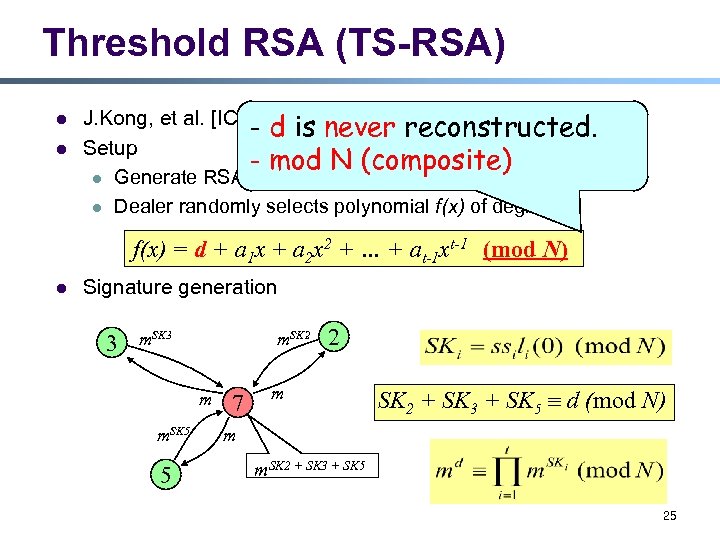
Threshold RSA (TS-RSA) l l J. Kong, et al. [ICNP’ 01, ISCC’ 02, WCMC’ 02] - d is never reconstructed. Setup - mod N (composite) l Generate RSA key pairs: d, e, N l Dealer randomly selects polynomial f(x) of degree t-1 f(x) = d + a 1 x + a 2 x 2 + … + at-1 xt-1 (mod N) l Signature generation 3 m. SK 2 m m. SK 5 5 7 2 m SK 2 + SK 3 + SK 5 d (mod N) m m. SK 2 + SK 3 + SK 5 25

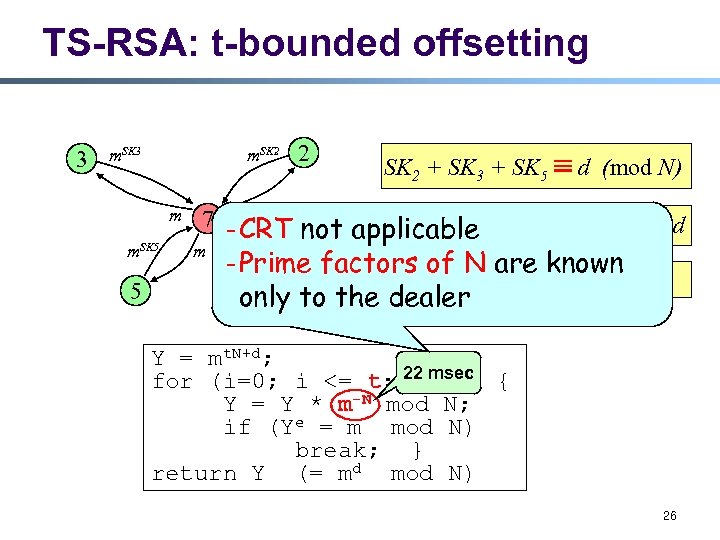
TS-RSA: t-bounded offsetting 3 m. SK 2 m m. SK 5 5 2 SK 2 + SK 3 + SK 5 d (mod N) m 7 - CRT not applicable SK 3 + SK 5 = t. N + d SK 2 + m - Prime factors of N are t. N+d = mt. Nmd known m. SK 2+SK 3+SK 5 = m SK 2 + SK 3 + SK 5 m only to the dealer Y = mt. N+d; for (i=0; i <= t; 22 msec { i++) -N mod N; Y = Y * m if (Ye = m mod N) break; } return Y (= md mod N) 26

TS-RSA: VSS failure l l Example: f(x) = 77 + 2 x + 5 x 2 (mod 119), g=3 Witnesses: w 0=377=12, w 1=32=9, w 2=35=5 (mod 119) 3 Impossible to detect pss (7)=74 2 malicious members, pssi(idno ssili(idj) mod N i. e, j) = 7 ss 7 = pss (7) robustness provided!2(7) + pss 3(7)+ pss 5(7) = 98 7 3 7 7 5 2 =71 pss 5(7)=72 Impossible to verify if ssi is correct. mod (N) (mod 119) 27

TS-RSA: Summary l No verifiability of secret shares l Gennaro [Crypto’ 96] and Shoup [Eurocrypt’ 00] proposed schemes to provide verifiability è l require trusted dealer to generate a key-pair Boneh & Franklin [Crypto’ 97] distributed RSA key generation è è l very high communication and/or computation overhead impractical in many group setting such as MANETs Trusted dealer involved at initialization phase 28

Threshold DSA (TS-DSA) l Extention of threshold DSS scheme by Jarecki, et al. [Eurocrypt’ 96] l group size (n) can be increased. l threshold (t) can be changed. l No dealer involved l VSS holds 29

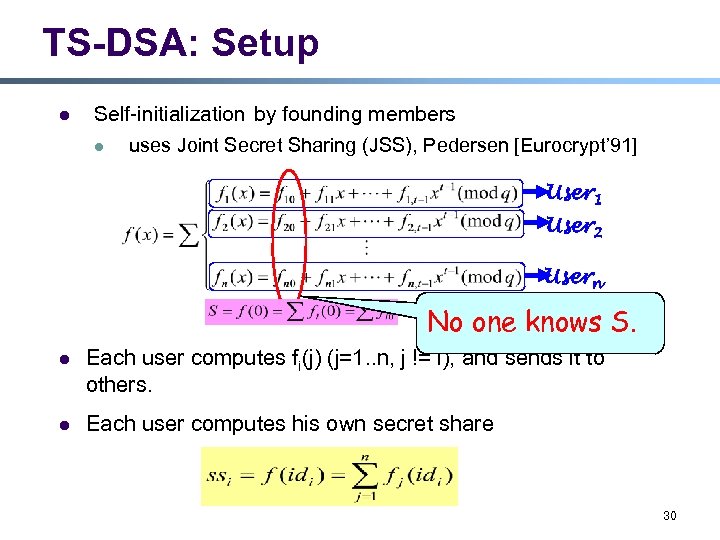
TS-DSA: Setup l Self-initialization by founding members l uses Joint Secret Sharing (JSS), Pedersen [Eurocrypt’ 91] User 1 User 2 Usern No one knows S. l Each user computes fi(j) (j=1. . n, j != i), and sends it to others. l Each user computes his own secret share 30

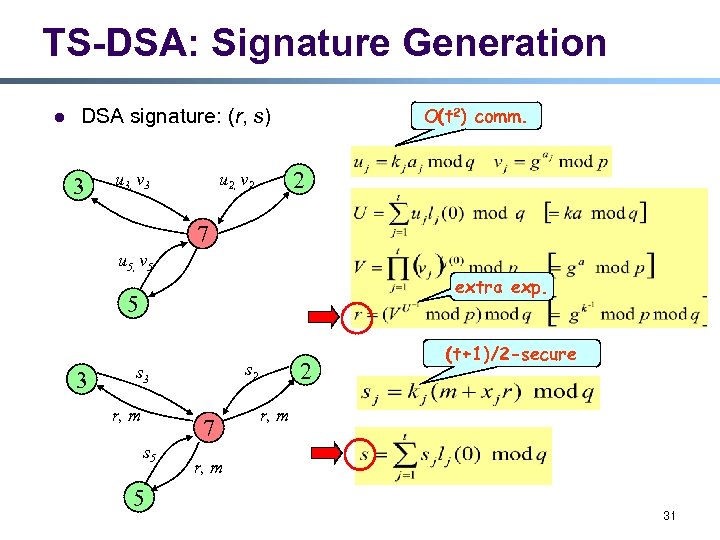
TS-DSA: Signature Generation l O(t 2) comm. DSA signature: (r, s) 3 u 3, v 3 2 u 2, v 2 7 u 5, v 5 extra exp. 5 3 r, m 7 s 5 5 2 s 3 (t+1)/2 -secure r, m 31

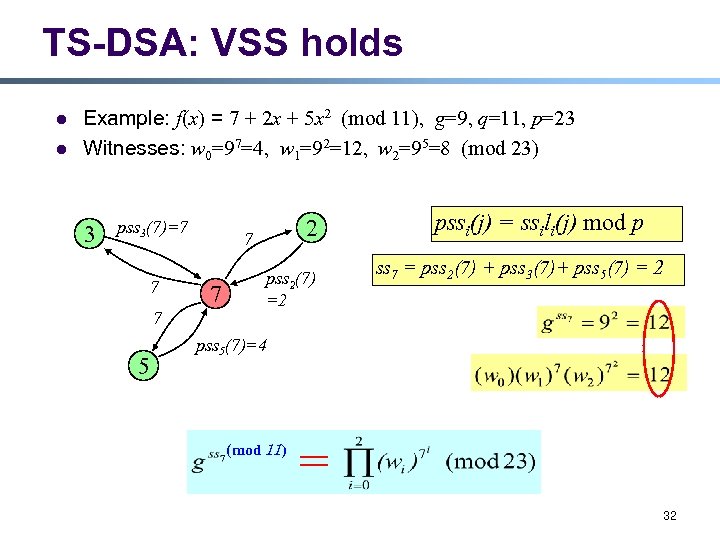
TS-DSA: VSS holds l l Example: f(x) = 7 + 2 x + 5 x 2 (mod 11), g=9, q=11, p=23 Witnesses: w 0=97=4, w 1=92=12, w 2=95=8 (mod 23) 3 pss 3(7)=7 7 7 5 2 7 7 pss 2(7) =2 pssi(j) = ssili(j) mod p ss 7 = pss 2(7) + pss 3(7)+ pss 5(7) = 2 pss 5(7)=4 (mod 11) 32

TS-DSA: Summary l Pros: l l l VSS guaranteed Key generation fully distributed Cons: l l Robust only if fewer than ë(t+1)/2û malicious users Extra O(t 2) communications between signers to jointly generate random secret k 33

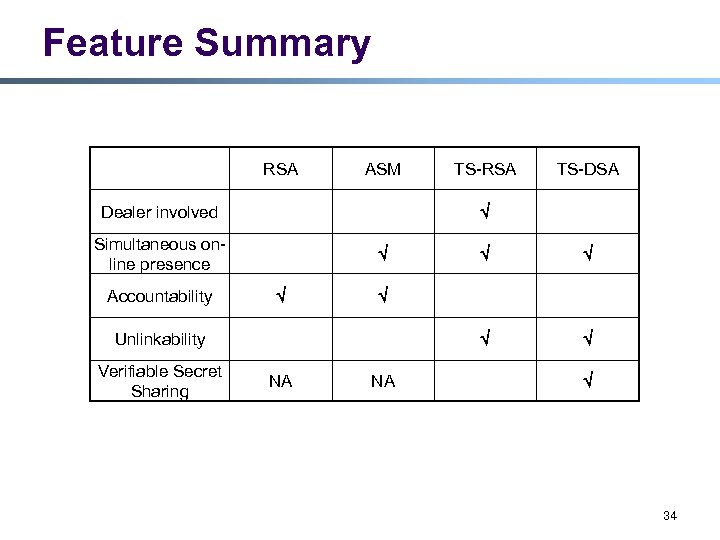
Feature Summary RSA ASM Simultaneous online presence NA Unlinkability Verifiable Secret Sharing TS-DSA Dealer involved Accountability TS-RSA NA 34

Outline l Introduction and Motivation l Admission Control l Distributed Cryptography l System Design and Integration l Performance Evaluation l Conclusion 35

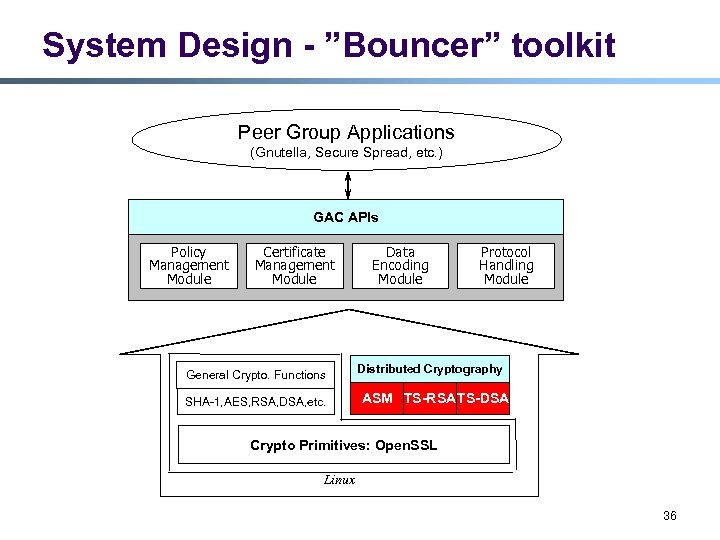
System Design - ”Bouncer” toolkit Peer Group Applications (Gnutella, Secure Spread, etc. ) GAC APIs Policy Management Module Certificate Management Module General Crypto. Functions SHA-1, AES, RSA, DSA, etc. Data Encoding Module Protocol Handling Module Distributed Cryptography ASM TS-RSATS-DSA Crypto Primitives: Open. SSL Linux 36

Dynamic Threshold Update 37

GAC APIs l Plain l l RSA APIs GAC_PACKET *PS_Join_Reqest(); GAC_PACKET *PS_Join_Commit(); GAC_PACKET *PS_GMC_Request(); /* optional */ GAC_PACKET *PS_GMC_Reply(); /* optional */ l TS-RSA l l l l TS-DSA l l l l l APIs GAC_PACKET *TSD_Join_Request(); GAC_PACKET *TSD_Join_Commit(); GAC_PACKET *TSD_Chal_Req(); GAC_PACKET *TSD_Chal_Rly(); GAC_PACKET *TSD_Rnd_Req(); GAC_PACKET *TSD_Rnd_Rly(); GAC_PACKET *TSD_Sign_Request(); GAC_PACKET *TSD_Part_Sign(); GAC_PACKET *TSD_GMC_Request(); /* optional */ GAC_PACKET *TSD_GMC_Reply(); /* optional */ GAC_PACKET *TSS_Join_Request(); GAC_PACKET *TSS_Join_Commit(); GAC_PACKET *TSS_Sign_Request(); GAC_PACKET *TSS_Part_Sign(); GAC_PACKET *TSS_GMC_Request(); /* optional */ GAC_PACKET *TSS_GMC_Reply(); /* optional */ l ASM l l l APIs GAC_PACKET *ASM_Join_Request(); GAC_PACKET *ASM_Join_Commit(); GAC_PACKET *ASM_Sign_Request(); GAC_PACKET *ASM_Part_Sign(); GAC_PACKET *ASM_GMC_Request(); /* optional */ GAC_PACKET *ASM_GMC_Reply(); /* optional */ 38

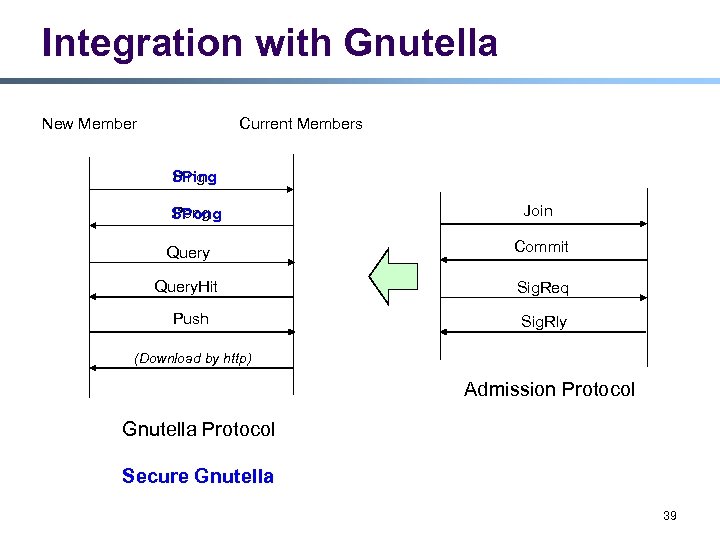
Integration with Gnutella New Member Current Members Ping SPing Pong SPong Join Query Commit Query. Hit Sig. Req Push Sig. Rly (Download by http) Admission Protocol Gnutella Protocol Secure Gnutella 39

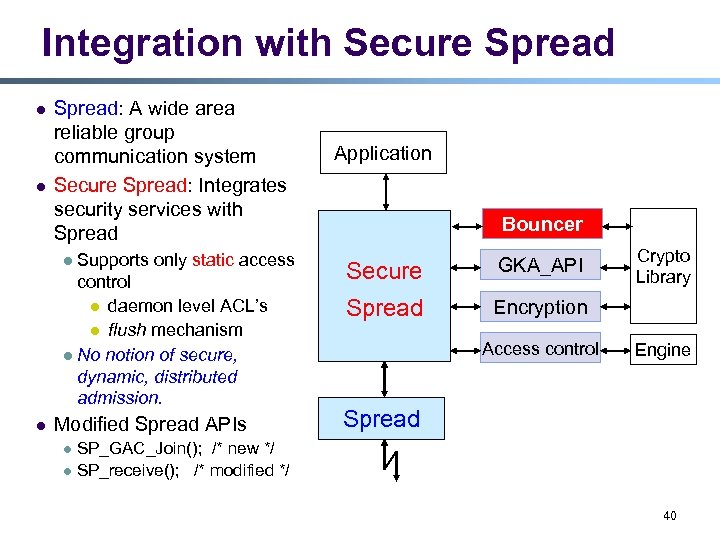
Integration with Secure Spread l l Spread: A wide area reliable group communication system Secure Spread: Integrates security services with Spread Supports only static access control l daemon level ACL’s l flush mechanism l No notion of secure, dynamic, distributed admission. l l Modified Spread APIs Application Bouncer Secure GKA_API Spread Crypto Library Encryption Access control Engine Spread SP_GAC_Join(); /* new */ l SP_receive(); /* modified */ l 40

Outline l Introduction and Motivation l Admission Control l Distributed Cryptography l System Design and Integration l Performance Evaluation l Conclusion 41

Performance Evaluation l Gnutella Experiment: l Integrated decentralized protocol with Gnut-0. 4. 21 l Tested on a high-speed LAN l Secure Spread Experiment: l Integrated centralized protocol with Secure SPREAD-2. 1. 0 l Spread daemons on 10 machines at Johns Hopkins Univ. l A client at UCI l Measurements l Fixed threshold l Dynamic threshold Source code available at http: //sconce. ics. uci. edu/gac 42

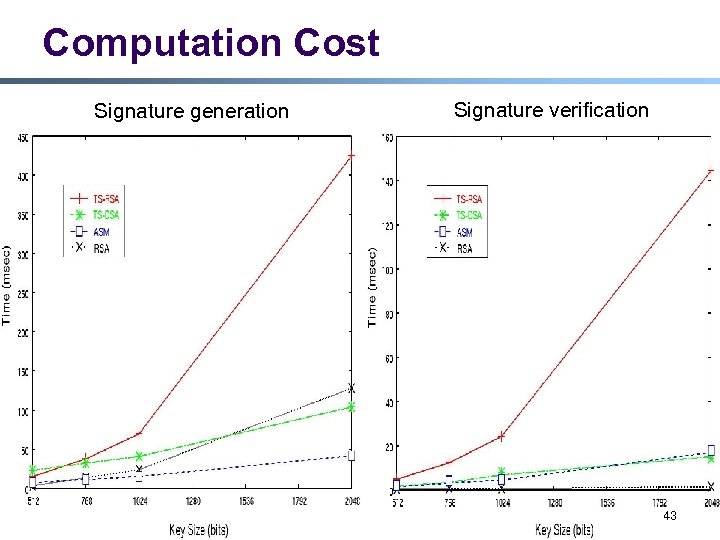
Computation Cost Signature generation Signature verification 43

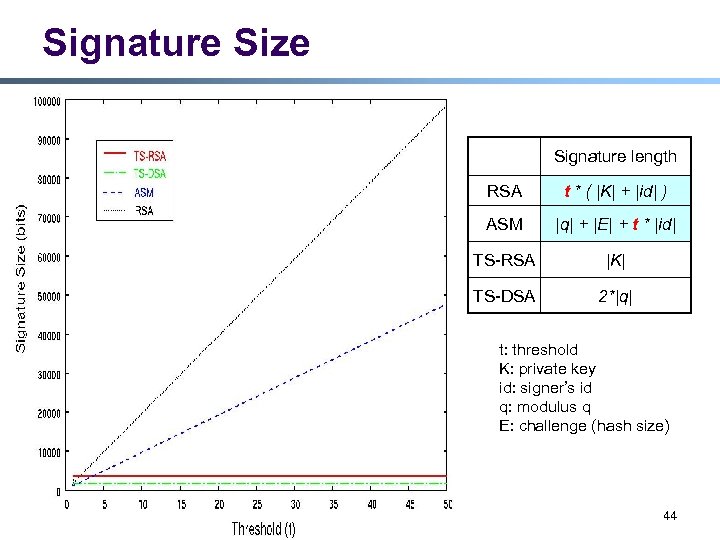
Signature Size Signature length RSA t * ( |K| + |id| ) ASM |q| + |E| + t * |id| TS-RSA |K| TS-DSA 2*|q| t: threshold K: private key id: signer’s id q: modulus q E: challenge (hash size) 44

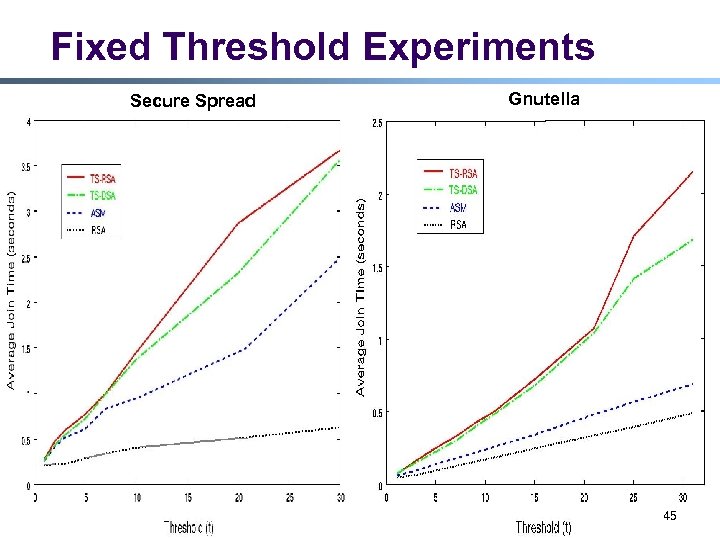
Fixed Threshold Experiments Secure Spread Gnutella 45

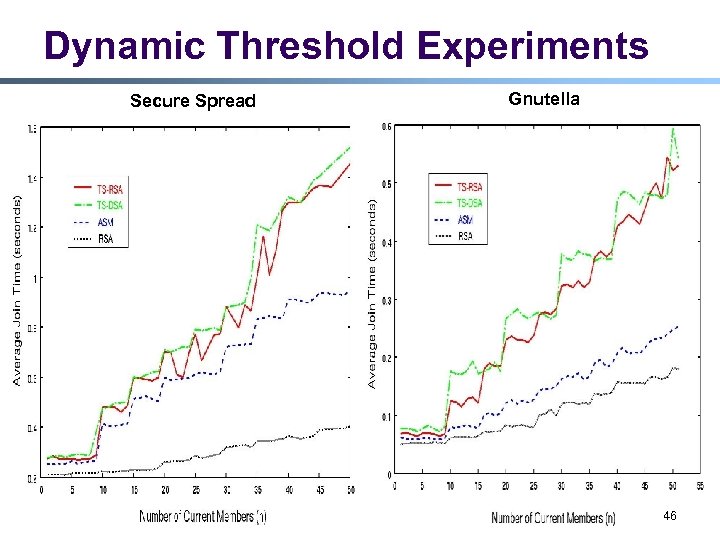
Dynamic Threshold Experiments Secure Spread Gnutella 46

Conclusions l Designed several P 2 P admission control mechanisms l Assessed practicality of distributed cryptography for dynamic peer groups. l Threshold signatures are currently NOT PRACTICAL in MANETs and sensor networks l Reasonable for Internet-based P 2 P systems that operate in (at least partially) synchronous mode l Difficult to identify one scheme best-suited for all peer group admission scenarios. l If admission is difficult, distributed membership revocation is even harder! 47

Future Work • TS-RSA • Efficient RSA distributed modulus generation • VSS in Dynamic setting • TS-DSA • Better communication efficiency? • Aggregated Signatures? • Other, more “systems” approaches? • Revocation? 48