Лекция 1_10_02_2014.ppt
- Количество слайдов: 160

Медицинская биостатистика Лекция 1 Статистика в диагностике Никита Николаевич Хромов-Борисов Кафедра физики, математики и информатики ПСПб. ГМУ им. акад. И. П. Павлова 8 -952 -204 -89 -49 (Теле 2); 8 -921 -449 -2905 (Мега. Фон) Nikita. Khromov. Borisov@gmail. com http: //independent. academia. edu/Nikita. Khromov. Borisov 1

1897 ПСПб. ГМУ Кафедра ФМИ 2

Зачем нужна статистика? 3

1897 ПСПб. ГМУ Кафедра ФМИ Проблема изменчивости и разнообразия (полиморфизма), индивидуальности и уникальности • Даже на уровне атомов одного и того же химического элемента имеет место разнообразие. • Большинство элементов являются смесью изотопов, некоторые из которых нестабильны - радиоактивны. • Человек как вид представлен уникальными особями, нет двух одинаковых людей. • Различаются даже монозиготные близнецы: отпечатками пальцев, варьирующими участками иммуноглобулинов, структурой межнейронных связей в мозгу и т. п. • Поэтому невозможно получить «чистые линии» человека. 4

1897 ПСПб. ГМУ Кафедра ФМИ Принцип близорукости • Физики и химики оперируют количествами вещества, определяемыми числом Авогадро (NA): в 1 моле любого вещества содержится 6· 1023 структурных единиц (атомов, молекул и т. п. ). • Даже в 1 наномоле вещества содержится «астрономическое» число таких единиц: 6· 1014. • А население Земли составляет 7, 095, 217, 980 (на июль 2013 по данным ЦРУ: CIA — The World Factbook), т. е. «всего лишь» 7· 109. • Принимая во внимание уникальность каждого человека, мы вынуждены закрывать глаза на некие «мелкие» различия. • В частности, модная ныне «персонализированная медицина» входит в противоречие с идеологией и методологий клинических испытаний, для которых требуются большие «однородные» выборки индивидуумов. 5

Повторение – мать познания: Проблема воспроизводимости результатов в биомедицине 6

1897 Begley C. G. , Ellis L. M. Raise standards for preclinical cancer research // Nature, 2012. Vol. 483. P. 531 -533. • Гленн Бегли (C. Glenn Begley), бывший вице-президент известной биотехнологической компании Amgen, и его коллега Ли Эллис (Lee M. Ellis) недавно сообщили, что ученые этой компании не смогли подтвердить (воспроизвести) результаты 47 из 53 статей, которые казались многообещающими для запуска программ по производству новых лекарств. • Бегли и Эллис считают, что плохая воспроизводимость результатов становится системной проблемой современной науки. • В одном исследовании, которое за короткий период цитировалось около 2000 раз, даже сами авторы впоследствии не смогли воспроизвести собственные результаты. ПСПб. ГМУ Кафедра ФМИ 7

Азы статистики 8

1897 ПСПб. ГМУ Кафедра ФМИ Статистика • Статистику можно определить как науку об изучении статистических данных • или • как науку об изменчивости результатов подсчетов и измерений в разных областях научной и практической деятельности человека. • Если вдуматься, то в силу неизбежной изменчивости результатов в биомедицине, фактически все ее выводы и доказательства являются вероятностно-статистическими. 9

1897 ПСПб. ГМУ Кафедра ФМИ Данные • Данные – это такие сведения, факты, информация, которые мы собираем и изучаем (анализируем) с какойлибо целью: • придти к какому-либо выводу, заключению или принять решение. • Решения часто бывают жизненно важными: • Лечит ли предлагаемое средство или метод или нет, или - напротив – наносит ли изучаемый агент вред, • правильно ли врач ставит диагноз, • есть ли связь (корреляция) между фактором риска и болезнью и т. п. 10

1897 ПСПб. ГМУ Кафедра ФМИ Два основных типа Статистических Данных • Существуют два основных типа численных данных: • измеряемые, или количественные данные (например, « 16 граммов» , « 4 сантиметра» ), и • подсчитываемые, или качественные данные (например, « 162 субъекта с данной болезнью» ). • Счетные и • Мерные • Счетные данные подсчитываются. • Мерные данные измеряются. 11

1897 ПСПб. ГМУ Кафедра ФМИ Пример: каковы признаки этой собаки? Качественные: Ее окрас - коричневый с черным У нее длинная шерсть Она энергичная Количественные: счетные: – У нее 4 ноги – У нее два брата • мерные: – Ее вес – 25, 5 кг – Ее рост (в холке) 56, 5 см • • • 12

1897 ПСПб. ГМУ Кафедра ФМИ Популяция и выборка • В медицине и в эпидемиологии термин Популяция является калькой с английского population - синоним статистического понятия «генеральная совокупность» , т. е. совокупность индивидуумов, из которой отбирается выборка. • Поскольку вероятностной моделью популяции является определенная случайная величина (вероятностная переменная), которая характеризуется определенным распределением, то с этой точки зрения удобно говорить о выборке из данного распределения. 13

1897 ПСПб. ГМУ Кафедра ФМИ Случайность выборки обуславливает ее репрезентативность • Один из важнейших вопросов, решаемых статистикой: • Действительно ли данная выборка отражает основные свойства (параметры) распределения, из которого она извлечена? • Другими словами, представительна ли (репрезентативна ли) имеющаяся выборка? • Если выборка случайная, то закон больших чисел (ЗБЧ) гарантирует ее репрезентативность. 14

1897 ПСПб. ГМУ Кафедра ФМИ Сколько же • Сколько лягушек придется перецеловать, пока не найдешь свою принцессу ? • Босс В. Лекции по математике. Т. 4: Вероятность, информация, статистика. М. : Ком. Книга, 2005. – 216 с. 15

1897 ПСПб. ГМУ Кафедра ФМИ • Теория вероятностей построена на костях. . . Правда, слава богу, кости эти игральные! • Лука Умищев Ушаков И. А. История науки сквозь призму озарений. Кн. 5: Этот случайный, случайный мир. . . – М. : Книжный дом «ЛИБРОКОМ» , 2010. – 152 с. 16

1897 ПСПб. ГМУ Кафедра ФМИ Статистика с доверием • Дает ли статистика нам право доверять ей? • Например, как проверить, является ли игральная кость правильной (симметричной, идеальной)? 17

Закон Больших Чисел - ЗБЧ Основа основ статистики 18

1897 ПСПб. ГМУ Кафедра ФМИ Якоб Бернулли (Jakob Bernoulli, 27. 12. 1654 — 16. 08. 1705) Джероламо (Джироламо, Иероним) Кардано (лат. Hieronymus Cardanus, итал. Girolamo Cardano, Gerolamo Cardano; 24. 09. 1501 — 21. 09. 1576) «Искусство предположений» 19

1897 ПСПб. ГМУ Кафедра ФМИ Пафнутий Львович Чебышёв (очень широко распространено неправильное произношение фамилии с ударением на первый слог — «Че бышев» ) (04[16]. 1821 — 26. 11[08. 12]. 1894) 20

1897 ПСПб. ГМУ Кафедра ФМИ Имитация многократного вбрасывания игральной кости: программа SUStats. jar http: //www. jsc. nildram. co. uk/examples/sustats/SUStats. html 21

1897 ПСПб. ГМУ Кафедра ФМИ Простейшая форма закона больших чисел - теорема Бернулли • Она утверждает, что если вероятность события P(A) неизменна во всех испытаниях, то с увеличением числа испытаний частота события f(A) все ближе сходится к его вероятности, т. е. частота становится все более устойчивой и все меньше отклоняется от вероятности. • Следствие: • Мы можем не знать значение вероятности события, но проведя по возможности как можно больше испытаний, мы можем использовать наблюдаемую частоту в качестве надежной статистической оценки этой неизвестной вероятности. 22

1897 ПСПб. ГМУ Кафедра ФМИ «Обратная сторона» ЗБЧ • Одновременно со сходимостью частоты к вероятности ситуация, когда частота события точно совпадет с его вероятностью: • становится все менее вероятной, • т. е. по мере увеличения числа испытаний вероятность такого точного совпадения сходится к нулю: 23

1897 ПСПб. ГМУ Кафедра ФМИ Вероятности точного совпадения частоты и вероятности при P(A) = φ = 0, 5 f(A) • • • 5/10 50/100 500/1000 5000/10000 50000/100000 500000/100000 Pr{f(A)} • • • 0, 25 0, 080 0, 025 0, 0080 0, 0025 0, 00080 Для наглядности значения вероятностей округлены до двух значащих цифр 24

Статистика в диагностике Статистический контроль качества диагностических тестов с бинарными исходами 25

1897 Что такое «Золотой стандарт» в диагностике? «Золотой стандарт» (или эталон сравнения) – такой диагностический тест, который максимально точно (практически безошибочно) определяет наличие или отсутствие определенной болезни у пациента. Например, при диагнозе рака одними из наиболее убедительных принято считать результаты гистологической диагностики. Эталонный метод диагностики совсем не обязательно должен быть единственным. Чаще всего это есть результат применения нескольких диагностических методов. ПСПб. ГМУ Кафедра ФМИ • • 26

1897 ПСПб. ГМУ Кафедра ФМИ Всё познается в сравнении • Золотой стандарт – желательный, но практически недостижимый идеал. • К тому же часто он бывает дорог, болезнен, рискован и потому его нецелесообразно (неэкономично) использовать в массовых обследованиях. • Очевидно, что и врач и пациент воздержатся от его применения, если им будет предложен другой более простой, щадящий, но не менее надежный метод диагностики. • Вопрос: как убедиться в надежности нового метода? • Ответ: надо сравнить результаты, получаемые с использованием предлагаемого теста, с результатами золотого стандарта. 27

1897 ПСПб. ГМУ Кафедра ФМИ Статистический анализ – фактически единственный надежный путь оценки качества и сравнения диагностических тестов • Диагностические тесты далеко не всегда дают верные ответы, и поэтому возникает необходимость выразить количественно, насколько точен, надежен и информативен данный тест. • Очевидно, что лучший и фактически единственный путь работать с несовершенной информацией – использовать статистические методы и выражать результаты диагноза и прогноза в терминах вероятности. • Поэтому следует осознавать, что диагностические тесты определяют не наличие или отсутствие болезни, но лишь их вероятности. 28

1897 ПСПб. ГМУ Кафедра ФМИ Основные схемы формирования выборок для статистического контроля качества диагностических тестов • 1. Одновыборочное (общепопуляционное - population-based) или поперечно-срезовое одномоментное (cross-sectional) формирование и исследование выборки. • 2. Двухвыборочное, при котором формируются две независимые случайные выборки по схеме «случаи – контроли» (case-control). 29

1897 ПСПб. ГМУ Кафедра ФМИ Одновыборочное исследование • При одновыборочной схеме из данной популяции отбирается одна случайная выборка субъектов без использования информации о наличии или отсутствии у них данной болезни. • Наличие или отсутствие болезни у отобранных субъектов определяется посредством применения эталонного средства ее диагностики уже после формирования исходной выборки. • Таким образом, после получения результатов золотого стандарта исходная случайная выборка субъектов подразделяется на две группы: субъекты с болезнью и без нее. 30

Пример: Ранняя диагностика рака молочной железы - Маммография 31
1897 ПСПб. ГМУ Кафедра ФМИ Маммограф Рабочая зона 32
1897 ПСПб. ГМУ Кафедра ФМИ Компьютеризированный маммограф 33

1897 ПСПб. ГМУ Кафедра ФМИ Процедура проведения маммографии 34
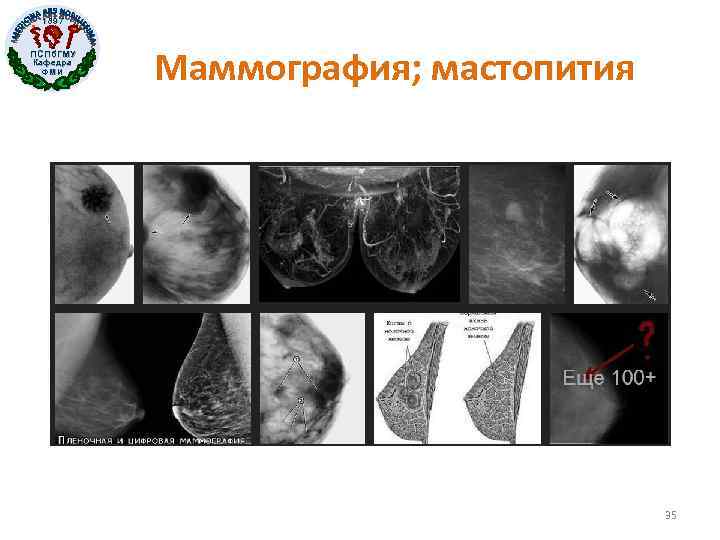
1897 ПСПб. ГМУ Кафедра ФМИ Маммография; мастопития 35
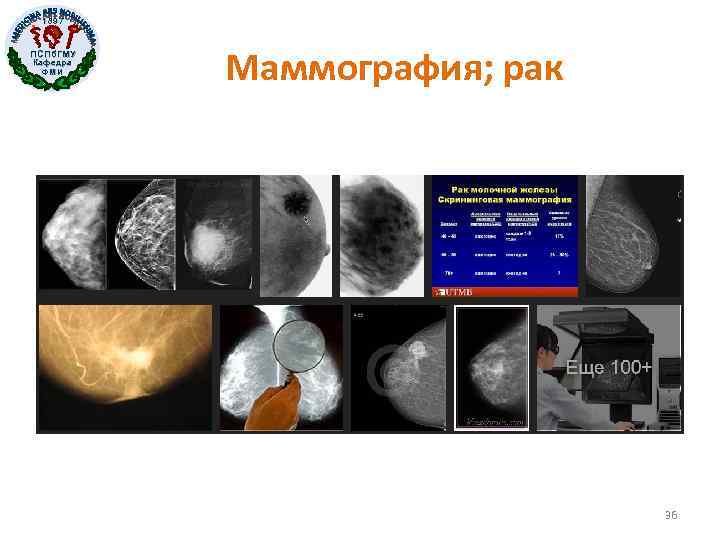
1897 ПСПб. ГМУ Кафедра ФМИ Маммография; рак 36

Насколько мы можем доверять результатам маммографических обследований? 37

1897 ПСПб. ГМУ Кафедра ФМИ Массовый маммографический скрининг • Banks E. , Reeves G. , Beral V. , Bull D. , Crossley B. , Simmond M. , Hilton E. , Bailey S. , Barret N. , Briers P. , Englis R. , Jackson A. , Kutt E. , Lavelle J. , Rockal L. , Wallis M. G. , Wilson M. , Patnick J. • Influence of personal characteristics of individual women on sensitivity and specificity of mammography in the Million Women Study: cohort study • BMJ, 2004; Vol. 329; No 7464; p. 477 • В медицине под скринингом понимают проведение простых и безопасных исследований больших групп населения с целью выделения групп риска развития той или иной патологии. 38
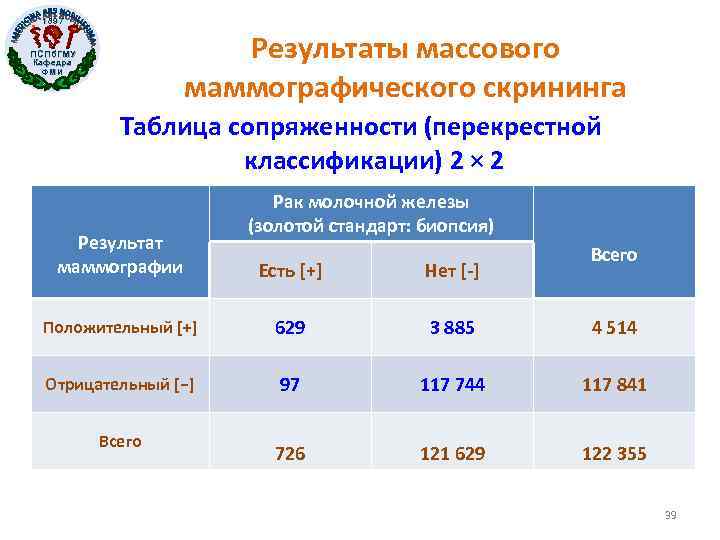
1897 Результаты массового маммографического скрининга ПСПб. ГМУ Кафедра ФМИ Таблица сопряженности (перекрестной классификации) 2 × 2 Результат маммографии Рак молочной железы (золотой стандарт: биопсия) Всего Есть [+] Нет [-] Положительный [+] 629 3 885 4 514 Отрицательный [−] 97 117 744 117 841 726 121 629 122 355 Всего 39

«Анатомия» таблиц 2× 2 в диагностических исследованиях 40
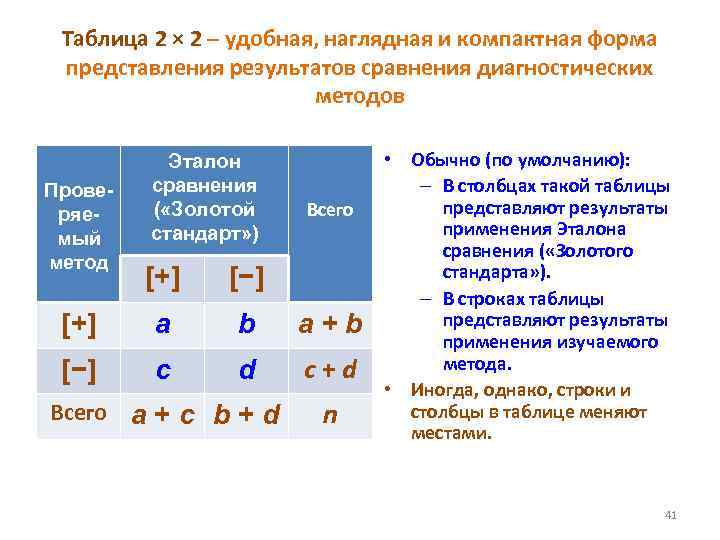
Таблица 2 × 2 – удобная, наглядная и компактная форма представления результатов сравнения диагностических методов Проверяемый метод Эталон сравнения ( «Золотой стандарт» ) Всего [+] [−] [+] a b a+b [−] c d c + d Всего a + c b + d n • Обычно (по умолчанию): – В столбцах такой таблицы представляют результаты применения Эталона сравнения ( «Золотого стандарта» ). – В строках таблицы представляют результаты применения изучаемого метода. • Иногда, однако, строки и столбцы в таблице меняют местами. 41

1897 ПСПб. ГМУ Кафедра ФМИ Основные обозначения для исходов диагностического исследования • D = результаты, полученные с использованием эталона сравнения (от англ. Disease). • D+ = наличие болезни по результатам, полученным с использованием эталона сравнения. • D- = отсутствие болезни по результатам, полученным с использованием эталона сравнения. • T = результаты, полученные с использованием проверяемого диагностического средства (от англ. Test). • T+ = «позитив» , т. е. положительный результат проверяемого теста. • T- = «негатив» , т. е. отрицательный результат проверяемого теста. 42
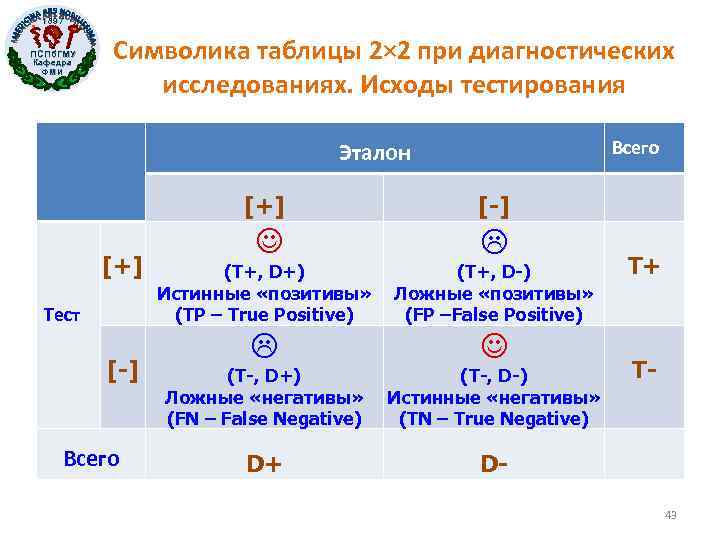
1897 ПСПб. ГМУ Кафедра ФМИ Символика таблицы 2× 2 при диагностических исследованиях. Исходы тестирования Всего Эталон [+] Тест [-] Всего [-] (T+, D+) Истинные «позитивы» (TP – True Positive) (T+, D-) Ложные «позитивы» (FP –False Positive) (T-, D+) Ложные «негативы» (FN – False Negative) (T-, D-) Истинные «негативы» (TN – True Negative) D+ D- T+ T- 43

Таблица 2 х 2: возможные исходы диагностического исследования и их наблюдаемые численности Проверяемый метод диагностики Эталон сравнения [+] • Всего [+] (T+) a+b [−] (T-, D+) (T-, D-) c. FN d. TN (T-) c + d (D+) a + c • a. TP – число истинных «позитивов» , т. е. верно положительных результатов тестов (T+, D+), • b. FP – число ложных «позитивов» , т. е. ошибочно положительных результатов теста (T+, D-), • с. FN – число ложных «негативов» , т. е. ошибочно отрицательных результатов теста (T-, D+), • d. TN – число истинных «негативов» , т. е. верно отрицательных результатов тестов (T-, D-) [−] (T+, D+) (T+, D-) a. TP b. FP Всего Наблюдаемые численности: (D-) b + d n 44
![1897 Вероятности исходов. Они нам неизвестны ПСПб. ГМУ Кафедра ФМИ Эталон [+] Тест [-] 1897 Вероятности исходов. Они нам неизвестны ПСПб. ГМУ Кафедра ФМИ Эталон [+] Тест [-]](https://present5.com/presentation/169138935_270038456/image-45.jpg)
1897 Вероятности исходов. Они нам неизвестны ПСПб. ГМУ Кафедра ФМИ Эталон [+] Тест [-] Всего [+] P(T+, D+) [-] P(T+, D-) P(T-, D+) P(T-, D-) P(T-) P(D+) P(D-) 1 P(T+) 45

Статистические оценки вероятностей в диагностических исследованиях 46

1897 ПСПб. ГМУ Кафедра ФМИ Статистическое оценивание – одна из основных задач статистики • Главная цель статистики – по возможности точно и надежно определить (вычислить) значение той или иной числовой характеристики (параметра) распределения, из которого извлечена выборка. • Материалом для этого служат имеющиеся статистические (выборочные) данные. 47

1897 ПСПб. ГМУ Кафедра ФМИ ЗБЧ обеспечивает точность оценок • Согласно ЗБЧ вычисляемые по данной выборке статистические оценки параметров (числовых характеристик, показателей) распределения, из которого извлечена выборка, по мере увеличения объема выборки будут все меньше отклоняться от значений оцениваемых (неизвестных нам) параметров популяции. • Например, в достаточно большой случайной выборке из однородной популяции доля субъектов с данным заболеванием может служить статистической оценкой распространённости этого заболевания. 48

1897 ПСПб. ГМУ Кафедра ФМИ Основная логика статистического оценивания: точечные оценки • Обычно вероятности P (или иные параметры) нам неизвестны. • Мы их оцениваем по наблюдаемым численностям: a, b, с и d. • Например, разумной и интуитивно понятной точечной оценкой для распространенности болезни по данным одновыборочного исследования P(D+) может служить наблюдаемая частота • f(D+) = (a + c) /n, • т. е. доля больных от общего числа n обследованных. 49

1897 Наблюдаем частоты f(A). Их мы признаем за статистические оценки неизвестных нам вероятностей P(A) ПСПб. ГМУ Кафедра ФМИ Эталон [+] Тест [-] Всего [+] f(T+, D+) [-] f(T+, D-) f(T-, D+) f(T-, D-) f(T-) f(D+) f(D-) 1 f(T+) 50

1897 ПСПб. ГМУ Кафедра ФМИ • • • Два основных типа статистических оценок Принципиальной особенностью выборочных данных является их изменчивость (варьирование). Поэтому при оценивании на их основе параметров распределения, из которого они извлечены, нельзя ограничиваться одним числом. Обязательно нужны еще оценки их варьирования. Поэтому различают два типа статистических оценок: Точечное оценивание – оценка одним числом. Интервальное оценивание – оценка интервалом. В статистике для интервального оценивания используются Доверительные Интервалы. Доверительный интервал — это такой интервал, который содержит (накрывает) неизвестный оцениваемый параметр с заданной вероятностью. Такая вероятность называется Доверительной Вероятностью или Уровнем Доверия. Уровень Доверия выбирается исследователем. 51

1897 ПСПб. ГМУ Кафедра ФМИ Точечные оценки доли • Частотническая: • Бейзовская: • если a priori 52

1897 ПСПб. ГМУ Кафедра ФМИ Основная логика статистического оценивания: интервальные оценки • Понятно, что если мы многократно повторим сравнения данного диагностического теста с эталоном сравнения, то наблюдаемые частоты f(Xi) неизбежно будут варьировать. • Поэтому задача математиков – вывести математический закон (вероятностное распределение), которому подчиняется варьирование этой частоты. • Если такой закон найден, то тогда можно получить доверительные интервалы (ДИ) для оценки вероятностей P(Xi) с заданной доверительной вероятностью (1 – α). 53

1897 ПСПб. ГМУ Кафедра ФМИ Частотнический доверительный интервал и доверительная вероятность • - вероятность того, что истинное, неизвестное нам значение параметра θunkn расположено внутри данного интервала. • - вероятность того, что истинное значение оцениваемого параметра θunkn расположено слева от нижней границы этого интервала слева. • - вероятность того, что истинное значение оцениваемого параметра θunkn расположено справа от верхней границы этого интервала слева. 54

1897 ПСПб. ГМУ Кафедра ФМИ Что такое Доверительный Интервал (ДИ)? • 100(1 – α)%-й Доверительный Интервал (ДИ) есть такой интервал, который с заданной доверительной вероятностью • (1 – α) • накрывает искомое оцениваемое значение параметра. • Принципиально важно понимать, что ДИ является случайным. • Это означает, что от опыта к опыту его границы будут колебаться, варьировать. 55
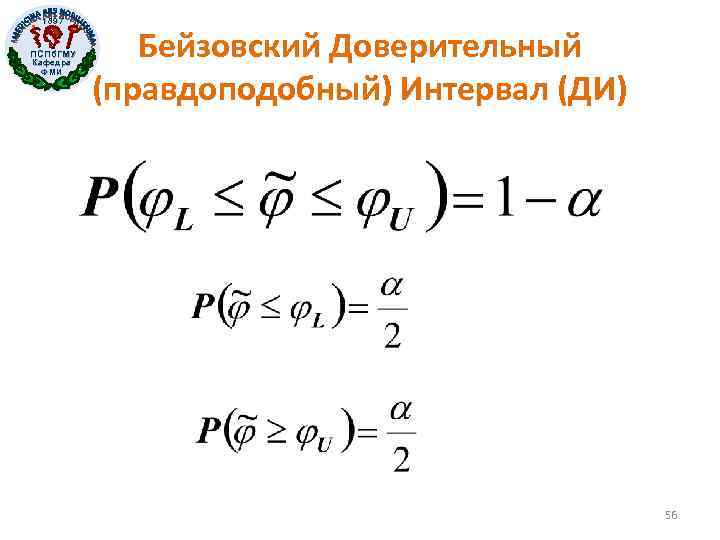
1897 ПСПб. ГМУ Кафедра ФМИ Бейзовский Доверительный (правдоподобный) Интервал (ДИ) 56
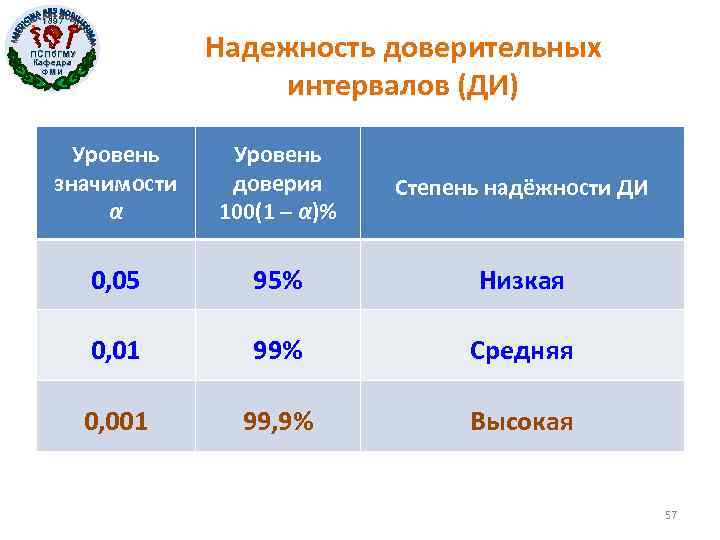
1897 Надежность доверительных интервалов (ДИ) ПСПб. ГМУ Кафедра ФМИ Уровень значимости α Уровень доверия 100(1 – α)% Степень надёжности ДИ 0, 05 95% Низкая 0, 01 99% Средняя 0, 001 99, 9% Высокая 57

1897 ПСПб. ГМУ Кафедра ФМИ Точность и надежность статистических оценок • Чем ýже ДИ, тем оценка точнее. • Поэтому показателем точности интервальной оценки может служить ширина доверительного интервала W = φU – φL. • Чем больше доверительная вероятность (1 – α), тем оценка надежнее. • Однако ДИ с доверительной вероятностью 100% - бессмыслен. • Например, 100%-й ДИ для доли будет содержать все значения в границах от 0 до 1: [0, 1]. 58

1897 ПСПб. ГМУ Кафедра ФМИ ДИ • Итак, например, 99%-й ДИ означает, что если мы многократно повторим наши наблюдения, то в 99% случаев получаемые интервалы накроют (неизвестное) значение оцениваемой вероятности P (или иного параметра θ). • Но в 1% случаев мы можем «промахнуться» : вычисленный интервал не накроет искомое значение. • И промах этот может случиться как раз с данной конкретной выборкой. • Отсюда мы приходим к выводу о неизбежной необходимости многократно повторять опыты (или наблюдения). 59

1897 ПСПб. ГМУ Кафедра ФМИ Наши жизненные достижения • Смысл « 99%-й доверительной вероятности» можно интерпретировать в терминах достижений нашей жизни. • Если мы за всю свою жизнь построили много 99%-х ДИ, то приблизительно 99% этих ДИ действительно содержали неизвестные оцениваемые значения. 60

1897 ПСПб. ГМУ Кафедра ФМИ Наши жизненные достижения • Поигрывая в картишки в доме престарелых и вспоминая свою жизнь, мы будем испытывать удовлетворение от того, что в 99% случаев наши ДИ были правильными. • Однако к этому чувству будет примешиваться огорчение, поскольку 1% интервалов были неверны. • И мы никогда не сможем узнать, в каких случаях результаты нашего труда были верны, а в каких нет! • Такова неизбежная неопределенность статистических выводов. • По: Сигел Э. Практическая бизнес-статистика. – М. : Издательский дом «Вильямс» , 2004. – 1056 с. (с. 418 -419) 61

1897 ПСПб. ГМУ Кафедра ФМИ Распознавание и предсказание • Не существует единого количественного показателя, с помощью которого можно было бы измерить способность диагностического теста распознавать и предсказывать наличие или отсутствие данной болезни. • • • Показатели качества диагностического теста удобно разделить на показатели его распознавательной способности и показатели его предсказательной способности, Они образуют две пары противоположностей: показатели и контр-показатели. • Только сопоставляя эти противоположности можно получить их содержательные интерпретации. 62

1897 ПСПб. ГМУ Кафедра ФМИ Основные вероятностные показатели распознавательной способности диагностического теста • Четыре показателя распознавательной способности образуют две пары противоположностей: • Чувствительность Se • и контр-чувствительность co. Se = 1 – Se. • Специфичность Sp • и контр-специфичность co. Sp = 1 – Sp. • Они являются условными вероятностями 63

1897 ПСПб. ГМУ Кафедра ФМИ • • • Условные вероятности Фактически все показатели распознавательной и предсказательной способностей диагностического теста являются условными вероятностями и функциями от них. По определению, условная вероятность события A при условии, что (уже) произошло событие B, есть результат деления вероятности совмещения обоих этих событий P(AB) на вероятность происшедшего события B: В формулах для обозначения условных вероятностей используется символ “|” - вертикальная черта. Читается и произносится как: «при условии, что» (или просто «при» ). Выражение читается как: «вероятность случайного события A при условии, что произошло событие B» (или «при условии, что утверждение B верно» ). 64

1897 ПСПб. ГМУ Кафедра ФМИ Что такое Чувствительность диагностического теста? • Чувствительность Se (от англ. Sensitivity) есть вероятность «позитива» у субъекта с болезнью: • P(T+|D+) = P(T+, D+)/[P(D+)] • Она является вероятностным показателем способности положительных результатов диагностического теста ( «позитивов» ) распознавать ( «чувствовать» ) наличие болезни. 65

1897 ПСПб. ГМУ Кафедра ФМИ Что такое Специфичность диагностического теста? • Специфичность Sp (от англ. Specificity) есть вероятность «негатива» у субъекта без болезни: • P(T-|D-) = P(T-, D-)/[P(D-)] • Она является вероятностным показателем способности отрицательных результатов диагностического теста ( «негативов» ) распознавать отсутствие болезни. 66
![1897 Идеал ПСПб. ГМУ Кафедра ФМИ Тест [+] [-] Эталон [+] a 0 [-] 1897 Идеал ПСПб. ГМУ Кафедра ФМИ Тест [+] [-] Эталон [+] a 0 [-]](https://present5.com/presentation/169138935_270038456/image-67.jpg)
1897 Идеал ПСПб. ГМУ Кафедра ФМИ Тест [+] [-] Эталон [+] a 0 [-] 0 d • В терминах чувствительности и специфичности, «Золотой стандарт» (Эталон сравнения) – это такой диагностический тест (метод), который одновременно обладает идеальными (100%ми) чувствительностью и специфичностью: • Se = a/(a + 0) = 100% • Sp = d/(0 + d) = 100% 67
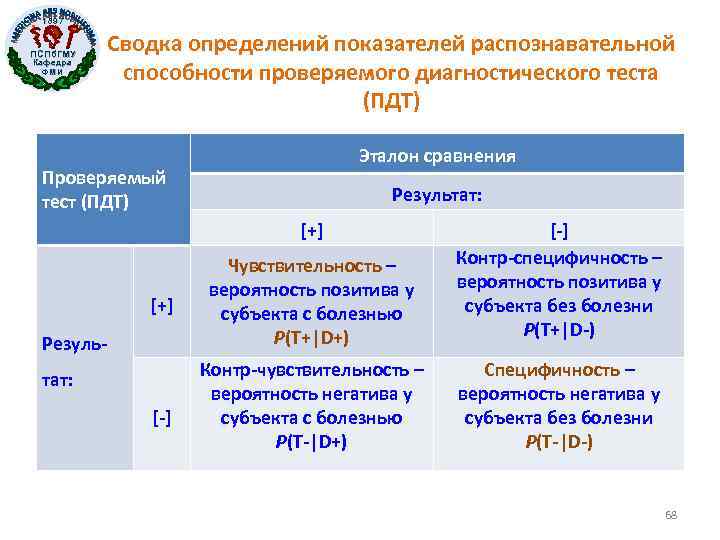
1897 ПСПб. ГМУ Кафедра ФМИ Сводка определений показателей распознавательной способности проверяемого диагностического теста (ПДТ) Эталон сравнения Проверяемый тест (ПДТ) Результат: [+] Результат: [-] Чувствительность – вероятность позитива у субъекта с болезнью P(T+|D+) [-] Контр-специфичность – вероятность позитива у субъекта без болезни P(T+|D-) Контр-чувствительность – вероятность негатива у субъекта с болезнью P(T-|D+) Специфичность – вероятность негатива у субъекта без болезни P(T-|D-) 68

1897 Бейзовские точечные оценки показателей распознавательной способности проверяемого диагностического теста (при равномерном приоре) ПСПб. ГМУ Кафедра ФМИ Проверяе- Эталон сравнения мый Результат: тест (ПДТ) Результат: Всего [+] [-] 1 1 [+] [-] 69

1897 ПСПб. ГМУ Кафедра ФМИ Идеальный и бесполезный тесты в терминах Se и Sp • Если тест идеальный, то • Se = 1 и Sp = 1. • Если • Se ≤ 0, 5 и Sp ≤ 0, 5, • то тест следует признать бесполезным. 70

1897 ПСПб. ГМУ Кафедра ФМИ Какие значения показателей распознавательной способности ПДТ следует считать неинформативными? • Неинформативным для чувствительности Se и контрчувствительности co. Se является значение • Seuninf = co. Seuninf = 0, 5. • Действительно: • Se = P(T+|D+) и co. Se = P(T-|D+), • и если они равны: • P(T+|D+) = P(T-|D+) = 0, 5, • то вряд ли ПДТ с такой чувствительностью можно признать приемлемым при выявлении «позитивов» у субъектов с болезнью. • Аналогично, неинформативным для специфичности Sp и контр-специфичности co. Sp, является значение: • Spuninf = co. Spuninf = 0, 5. 71

1897 ПСПб. ГМУ Кафедра ФМИ Неинформативные значения показателей распознавательной способности проверяемого диагностического теста (ПДТ) Проверяемый диагностический тест (ПДТ) Результат: Всего Эталон сравнения Результат: [+] [-] [+] Seuninf = 0, 5 co. Spuninf = 0, 5 [-] co. Seuninf = 0, 5 1 Spuninf = 0, 5 1 72

1897 ПСПб. ГМУ Кафедра ФМИ Возможные словесные интерпретации для градаций Se и Sp Se = P(T+|D+) Чувствительность «позитивов» к наличию болезни 0, 0 – 0, 5 Практически бесполезная 0, 5 – 0, 7 Низкая 0, 7 – 0, 9 Средняя 0, 9 – 1, 0 Высокая Sp = P(T-|D-) Специфичность «негативов» в отношении отсутствия болезни 73

1897 ПСПб. ГМУ Кафедра ФМИ Логика использования доверительных интервалов для оценки статистической значимости полученных результатов • 100(1 – α)%-й ДИ является интервальной оценкой неизвестного нам показателя (параметра) φunkn с заранее выбранной нами доверительной вероятностью 100(1 – α)%. • Если 100(1 – α)%-й ДИ не накрывает неинформативное значение оцениваемого показателя (параметра), тогда приходят к выводу, что оцениваемое значение φ unkn статистически значимо отличается от неинформативного. • При этом добавляют, что отличие значимо на выбранном уровне значимости α. • Когда же 100(1 – α)%-й ДИ накрывает неинформативное значение оцениваемого показателя, то делают вывод, что оцениваемое значение φunkn статистически не отличается от неинформативного (на данном уровне значимости α). 74
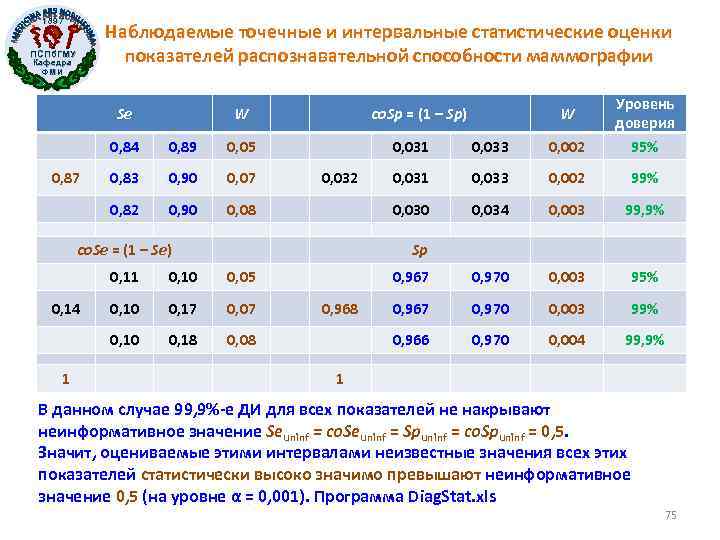
1897 Наблюдаемые точечные и интервальные статистические оценки показателей распознавательной способности маммографии ПСПб. ГМУ Кафедра ФМИ Se 0, 84 0, 89 0, 83 0, 90 0, 07 0, 90 0, 031 0, 033 0, 002 99% 0, 034 0, 003 99, 9% 0, 967 0, 970 0, 003 95% 0, 967 0, 970 0, 003 99% 0, 966 0, 970 0, 004 99, 9% W Sp 0, 11 0, 10 0, 05 0, 10 0, 17 0, 07 0, 10 1 0, 002 0, 030 0, 08 0, 032 co. Se = (1 – Se) 0, 14 0, 033 Уровень доверия 95% co. Sp = (1 – Sp) 0, 05 0, 82 0, 87 0, 031 W 0, 18 0, 08 0, 968 1 В данном случае 99, 9%-е ДИ для всех показателей не накрывают неинформативное значение Seuninf = co. Seuninf = Spuninf = co. Spuninf = 0, 5. Значит, оцениваемые этими интервалами неизвестные значения всех этих показателей статистически высоко значимо превышают неинформативное значение 0, 5 (на уровне α = 0, 001). Программа Diag. Stat. xls 75

1897 ПСПб. ГМУ Кафедра ФМИ • Когда в нашем распоряжении имеются оценки чувствительности и специфичности маммографического обследования, мы можем сообщить пациентке лишь следующее: • «если у Вас рак, то вероятность того, что результат Вашего маммографического обследования будет положительным, равна 87%. • Если же у Вас нет рака, то вероятность того, что результат Вашего маммографического обследования будет отрицательным, равна 97%» . 76

1897 ПСПб. ГМУ Кафедра ФМИ Предсказательная способность диагностического теста • Получив у данного пациента положительный (или отрицательный) результат данного диагностического теста, мы более всего заинтересованы получить ответ на основной прагматический вопрос: • Какова вероятность того, что у этого пациента действительно имеется (или действительно отсутствует) данная болезнь? • Статистическая оценка такой вероятности называется предсказательной вероятностью положительного (или отрицательного) результата теста. • Синонимы: предсказательность, прогностичность; предсказательная, прогнозирующая, прогностическая ценность диагностического теста, пост-тестовая вероятность, • По-английски: PPV – Positive Predictive Value (of a test) и NPV – Negative Predictive Value (of a test). 77

1897 ПСПб. ГМУ Кафедра ФМИ Проверьте свою интуицию • Допустим, что у женщины (не дай бог) маммография дала положительный результат. • Как Вы думаете, какова вероятность того, что у этой женщины действительно рак молочной железы, если оценки чувствительности и специфичности маммографии суть Se = 87% и Sp = 97%? 78

1897 ПСПб. ГМУ Кафедра ФМИ Принципиально важно • Принципиально важно понимать, что • P(T+|D+), • т. е. вероятность получить у субъекта положительный результат теста (T+) при условии наличия у него болезни (D+), не тождественна • P(D+|T+), • т. е. вероятность наличия у субъекта данной болезни, при условии получения у него положительного результата теста. 79

1897 ПСПб. ГМУ Кафедра ФМИ N. B. – nota bene • P(D+|T+) ≠ P(T+|D+) 80

1897 ПСПб. ГМУ Кафедра ФМИ P(L|D) ≠ P(D|L) • Если у субъекта диагностирована смертельная неизлечимая болезнь, допустим, прионная энцефалопатия – Болезнь Кройтцфельдта-Якоба (D), то вероятность летального исхода (L) в течение одного года очень велика, практически 100%: • P(L|D) = 100% • Но если перед нами труп, то вероятность того, что причиной смерти является именно эта болезнь очень мала: • P(D|L) = 10 -6 = 0, 0001% 81

1897 ПСПб. ГМУ Кафедра ФМИ Основные вероятностные показатели предсказательной способности диагностического теста • Четыре показателя предсказательной способности образуют две пары противоположностей: • предсказательность «позитивов» PPV • и их контр-предсказательность co. PPV = 1 – PPV • предсказательность «негативов» NPV • и их контр-предсказательность co. NPV = 1 – NPV Они также являются условными вероятностями 82
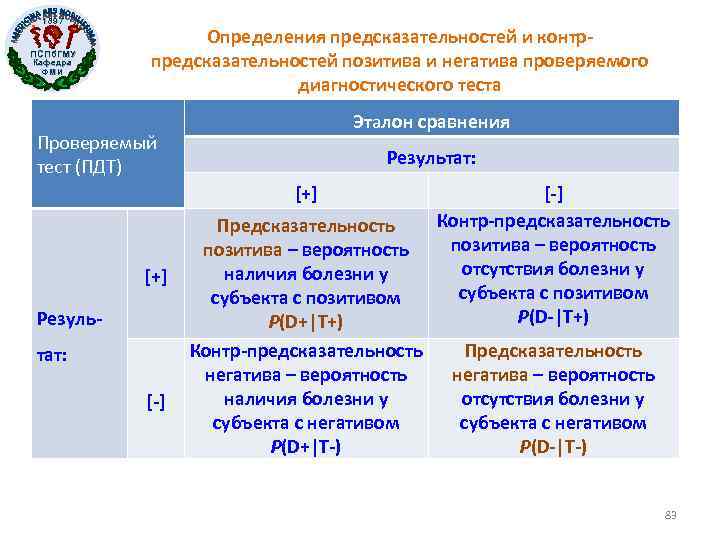
1897 ПСПб. ГМУ Кафедра ФМИ Определения предсказательностей и контрпредсказательностей позитива и негатива проверяемого диагностического теста Эталон сравнения Проверяемый тест (ПДТ) Результат: [+] Результат: [-] Предсказательность позитива – вероятность наличия болезни у субъекта с позитивом P(D+|T+) Контр-предсказательность негатива – вероятность наличия болезни у субъекта с негативом P(D+|T-) [-] Контр-предсказательность позитива – вероятность отсутствия болезни у субъекта с позитивом P(D-|T+) Предсказательность негатива – вероятность отсутствия болезни у субъекта с негативом P(D-|T-) 83

1897 ПСПб. ГМУ Кафедра ФМИ Бейзовские точечные оценки показателей предсказательной способности ПДТ в одновыборочном исследовании (при равномерном приоре) Эталон сравнения Проверяемый тест (ПДТ) Всего Результат: [+] [-] [+] 1 Результат: [-] 1 84

1897 ПСПб. ГМУ Кафедра ФМИ Что такое Распространенность болезни, Prev = P(D+)? Вероятность обнаружить пациента с данной болезнью в данной популяции: P(D+) называется распространенностью болезни. Ее оценкой является доля, f(D+), лиц с данной болезнью в выборке объемом n из данной популяции, выявленных с помощью золотого стандарта. Два варианта оценки распространенности: 1. Данные демографической (медицинской) статистики. 2. Общепопуляционное исследование - исследование, в котором из данной популяции отбирают случайным образом большую группу людей (репрезентативную выборку). 85
![Оценка распространенности болезни при одновыборочном исследовании Проверяемый метод диагностики Эталон сравнения [+] [−] Всего Оценка распространенности болезни при одновыборочном исследовании Проверяемый метод диагностики Эталон сравнения [+] [−] Всего](https://present5.com/presentation/169138935_270038456/image-86.jpg)
Оценка распространенности болезни при одновыборочном исследовании Проверяемый метод диагностики Эталон сравнения [+] [−] Всего [+] (T+, D+) (T+, D-) (T+) a+b a b [−] (T-) (T-, D+) (T-, D-) c + d c d Всего (D+) (D-) a + c b + d n Вероятность обнаружить пациента с данной болезнью в данной популяции: P(D+). В одновыборочном исследовании ее оценкой является доля лиц с данной болезнью в выборке объемом n из данной популяции: f(D+), выявленных с помощью золотого стандарта. В одновыборочном исследовании она вычисляется как отношение количества больных (a + c), выявленных с помощью золотого стандарта, в данной выборке, к общему числу обследованных n: Prev = f(D+) = (a + c)/n Или Prev = f(D+) = (a + c +1)/(n + 2) 86
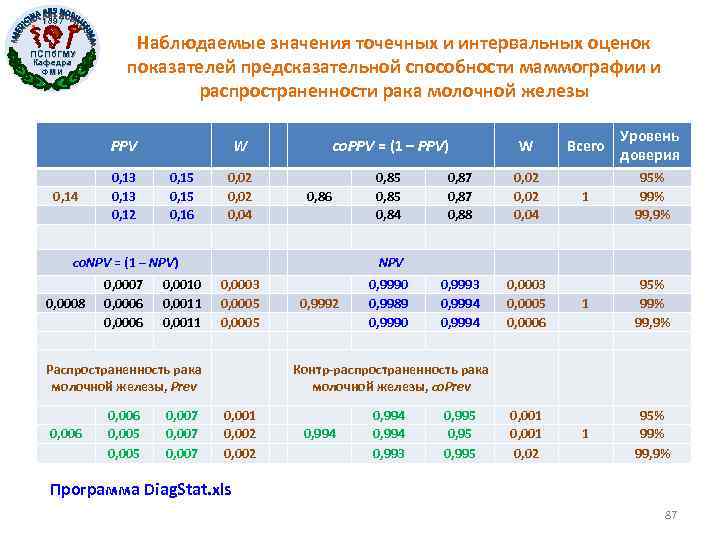
1897 ПСПб. ГМУ Кафедра ФМИ Наблюдаемые значения точечных и интервальных оценок показателей предсказательной способности маммографии и распространенности рака молочной железы PPV 0, 14 0, 13 0, 12 W 0, 15 0, 16 co. PPV = (1 – PPV) W 0, 02 0, 04 0, 85 0, 84 0, 87 0, 88 0, 02 0, 04 0, 9993 0, 9994 0, 0003 0, 0005 0, 0006 0, 86 co. NPV = (1 – NPV) 0, 0008 0, 0007 0, 0006 0, 0010 0, 0011 0, 006 0, 007 Уровень доверия 1 95% 99% 99, 9% 1 95% 99, 9% NPV 0, 0003 0, 0005 Распространенность рака молочной железы, Prev 0, 006 0, 005 Всего 0, 9992 0, 9990 0, 9989 0, 9990 Контр-распространенность рака молочной железы, co. Prev 0, 001 0, 002 0, 994 0, 993 0, 995 0, 001 0, 02 Программа Diag. Stat. xls 87

1897 ПСПб. ГМУ Кафедра ФМИ Статистическая значимость отличия PPV от Prev • В данном случае 99, 9%-го ДИ для PPV (от 0, 13 до 0, 15) не пересекается с 99, 9%-м ДИ для Prev (от 0, 005 до 0, 007). • Следовательно, оцениваемое значение PPV статистически высоко значимо отличается от распространенности рака молочной железы в обследованной популяции (на уровне α = 0, 001). 88

1897 ПСПб. ГМУ Кафедра ФМИ Идеальный и бесполезный тесты в терминах PPV и NPV • В терминах предсказательных вероятностей: • Если тест идеальный, то • PPV = 1 и NPV = 1. • Если • PPV ≤ 0, 5 и NPV ≤ 0, 5, • то тест следует признать бесполезным. 89

1897 ПСПб. ГМУ Кафедра ФМИ Неинформативные значения показателей предсказательной способности проверяемого диагностического теста (ПДТ) Проверяемый диагностический тест (ПДТ) Результат: Эталон сравнения Всего Результат: [+] [-] [+] PPVuninf = 0, 5 co. PPVuninf = 0, 5 1 [-] co. NPVuninf = 0, 5 1 90

1897 ПСПб. ГМУ Кафедра ФМИ Возможные словесные интерпретации для градаций PPV и NPV PPV = P(D+|T+) Способность «позитивов» предсказывать наличие болезни 0, 0 – 0, 5 Практически бесполезная 0, 5 – 0, 7 Низкая 0, 7 – 0, 9 Средняя 0, 9 – 1, 0 Высокая NPV = P(D-|T-) Способность «негативов» предсказывать отсутствие болезни 91

1897 ПСПб. ГМУ Кафедра ФМИ Компактная форма записи для совместного представления точечных и интервальных оценок • Пример: – Точечная оценка чувствительности маммографии: 0, 87 – Нижняя граница 99, 9%-го доверительного интервала (ДИ): 0, 83 – Верхняя граница 99, 9%-го ДИ: 0, 90 • Компактная запись: • 0, 820, 870, 90 92

1897 ПСПб. ГМУ Кафедра ФМИ До и после получения позитива • Статистическая оценка вероятности наличия рака молочной железы до маммографического обследования равна оценке его распространенности: • Prev = f(D+) = 0, 0050, 0060, 007. • После получения позитива 99, 9%-й ДИ для предсказательной вероятности наличия у пациентки рака • PPV = f(D+|T+) = 0, 120, 140, 16 • не перекрывается с 99, 9%-м ДИ для распространенности. • Следовательно, оцениваемое этим интервалом неизвестное значение PPV статистически высоко значимо превышает распространенность болезни. 93

1897 ПСПб. ГМУ Кафедра ФМИ Контр-прогностичность позитивов • Однако оно статистически значимо МЕНЬШЕ неинформативного значения 0, 5, и мы приходим к выводу о практической непригодности положительных результатов маммографии для надежного предсказания наличия рака молочной железы. • Этот вывод становится очевидным, если обратиться к статистической оценке контр-прогностичности позитивов, которая составила: • co. PPV = f(D-|T+) = (1 – PPV) = 0, 860, 88 • Таким образом, получается, что наличие позитива свидетельствует не столько о наличии рака молочной железы, сколько о его отсутствии. 94

1897 ПСПб. ГМУ Кафедра ФМИ До и после получения негатива • Статистическая оценка вероятности отсутствия рака молочной железы до маммографического обследования равна оценке его контр-распространенности: • co. Prev = f(D-) = 0, 9930, 9940, 995 или 99, 41%. • После получения негатива оценка предсказательной вероятности отсутствия у пациентки рака статистически значимо повышается и становится равной: • NPV = f(D-|T-) = 0, 99890, 99920, 9994 или 99, 92%. • Соответственно, оценка контр-предсказательности негативов получается очень малой: • co. NPV = (1 – NPV) = f(D+|T-) = 0, 00060, 00080, 0011 или 0, 08%. 95

1897 ПСПб. ГМУ Кафедра ФМИ Отношения правдоподобий • Между показателями распознавательной и предсказательной способностей ПДТ имеет место взаимозависимость, которая определяется четырьмя объединяющими их показателями качества диагностического теста, называемыми отношениями правдоподобий. • Они также образуют две взаимно инвертированные пары: • отношение правдоподобий для «позитивов» LR[+] и его инверсия inv. LR[+] = 1/LR[+], • отношение правдоподобий для «негативов» LR[-] и его инверсия inv. LR[+] = 1/LR[-]. 96
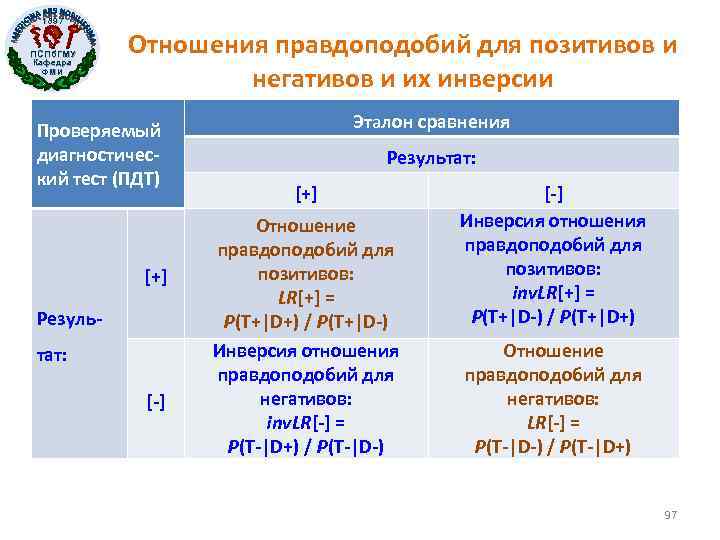
1897 ПСПб. ГМУ Кафедра ФМИ Отношения правдоподобий для позитивов и негативов и их инверсии Проверяемый диагностический тест (ПДТ) [+] Результат: [-] Эталон сравнения Результат: [+] Отношение правдоподобий для позитивов: LR[+] = P(T+|D+) / P(T+|D-) Инверсия отношения правдоподобий для негативов: inv. LR[-] = P(T-|D+) / P(T-|D-) [-] Инверсия отношения правдоподобий для позитивов: inv. LR[+] = P(T+|D-) / P(T+|D+) Отношение правдоподобий для негативов: LR[-] = P(T-|D-) / P(T-|D+) 97

1897 ПСПб. ГМУ Кафедра ФМИ Идеальный и бесполезный тесты в терминах LR • Если тест идеальный, то • LR[+] = и LR[-] = . • Если • LR[+] ≤ 1 и LR[-] ≤ 1, • то тест следует признать бесполезным. 98
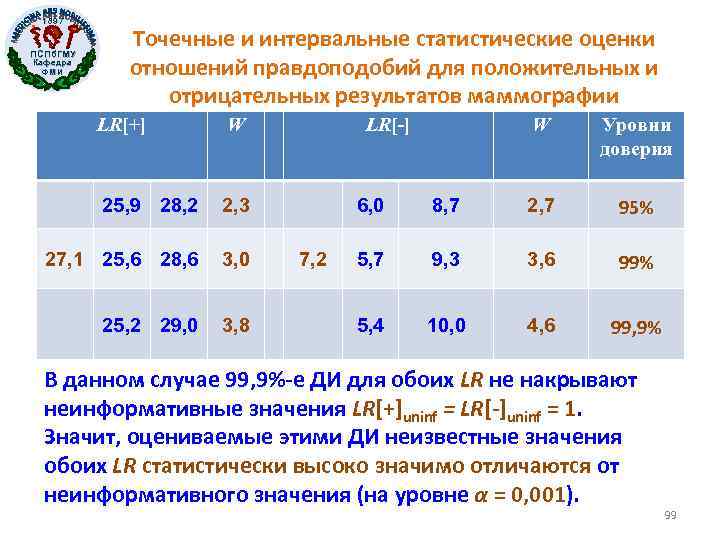
1897 ПСПб. ГМУ Кафедра ФМИ Точечные и интервальные статистические оценки отношений правдоподобий для положительных и отрицательных результатов маммографии LR[+] W 25, 9 28, 2 2, 3 27, 1 25, 6 28, 6 3, 0 25, 2 29, 0 3, 8 LR[-] W Уровни доверия 6, 0 7, 2 8, 7 2, 7 95% 5, 7 9, 3 3, 6 99% 5, 4 10, 0 4, 6 99, 9% В данном случае 99, 9%-е ДИ для обоих LR не накрывают неинформативные значения LR[+]uninf = LR[-]uninf = 1. Значит, оцениваемые этими ДИ неизвестные значения обоих LR статистически высоко значимо отличаются от неинформативного значения (на уровне α = 0, 001). 99
![1897 ПСПб. ГМУ Кафедра ФМИ Две интерпретации LR • LR[+] показывает, во сколько раз 1897 ПСПб. ГМУ Кафедра ФМИ Две интерпретации LR • LR[+] показывает, во сколько раз](https://present5.com/presentation/169138935_270038456/image-100.jpg)
1897 ПСПб. ГМУ Кафедра ФМИ Две интерпретации LR • LR[+] показывает, во сколько раз чаще позитивы будут получаться у субъектов с болезнью, чем у субъектов без болезни. • LR[-] показывает, во сколько раз чаще негативы будут получаться у субъектов без болезни, чем у субъектов с болезнью. • В то же время отношение правдоподобий показывает, во сколько различаются претестовые (априорные) и посттестовые (апостериорные) шансы за/против ( «одды» - odds). 100

1897 ПСПб. ГМУ Кафедра ФМИ Что такое «шансы за/против» ( «одды» ) для случайного события? • Два английских слова chance и odds на русский переводятся фактически одинаково: «шанс» и «шансы» . • Это создает трудности в их понимании. • Поэтому здесь для термина odds предлагается использовать уточняющее словосочетание «шансы за/против» . • Шансы за/против события A есть отношение вероятности осуществления этого события P(A) к вероятности его неосуществления P(Ā): • O(A) = P(A) / P(Ā) = P(A) / [1 – P(A)] 101

1897 ПСПб. ГМУ Кафедра ФМИ LR в терминах шансов за/против ( «оддов» ) • LR[+] • есть отношение посттестовых шансов за/против наличия болезни к претестовым шансам у субъекта с «позитивом» . • LR[-] • есть отношение посттестовых шансов за/против отсутствия болезни к претестовым шансам у субъекта с «негативом» . 102

1897 ПСПб. ГМУ Кафедра ФМИ 103
![1897 Принятые словесные интерпретации для градаций LR[+] и LR[-] ПСПб. ГМУ Кафедра ФМИ LR[+] 1897 Принятые словесные интерпретации для градаций LR[+] и LR[-] ПСПб. ГМУ Кафедра ФМИ LR[+]](https://present5.com/presentation/169138935_270038456/image-104.jpg)
1897 Принятые словесные интерпретации для градаций LR[+] и LR[-] ПСПб. ГМУ Кафедра ФМИ LR[+] Повышение посттестовых шансов за/против наличия болезни у субъекта с позитивом по сравнению с претестовыми шансами за/против наличия у него болезни 1 – 3 Практически ничтожное 3 – 10 Малое 10 – 33 Среднее 33 – 100 Высокое 100 – 1000 Очень высокое > 1000 Практически идеальное LR[-] Повышение посттестовых шансов за/против отсутствия болезни у субъекта с негативом по сравнению с претестовыми шансами за/против отсутствия у него болезни 104
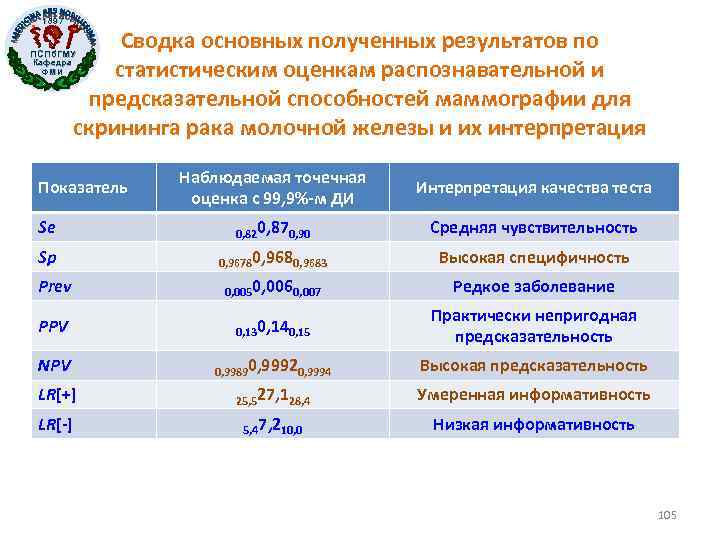
1897 Сводка основных полученных результатов по статистическим оценкам распознавательной и предсказательной способностей маммографии для скрининга рака молочной железы и их интерпретация ПСПб. ГМУ Кафедра ФМИ Наблюдаемая точечная оценка с 99, 9%-м ДИ Интерпретация качества теста Se 0, 820, 870, 90 Средняя чувствительность Sp 0, 96780, 9683 Высокая специфичность Prev 0, 0050, 0060, 007 Редкое заболевание PPV 0, 130, 140, 15 Практически непригодная предсказательность NPV 0, 99890, 99920, 9994 Высокая предсказательность LR[+] 25, 527, 128, 4 Умеренная информативность LR[-] 5, 47, 210, 0 Низкая информативность Показатель 105

1897 ПСПб. ГМУ Кафедра ФМИ Полезное правило • Где и когда только возможно, следует визуализировать результаты статистического анализа, т. е. представлять их наглядно – графически. 106
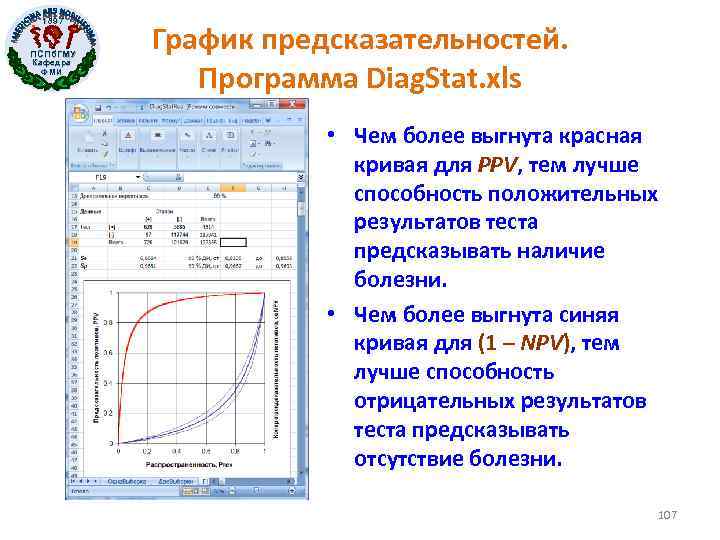
1897 ПСПб. ГМУ Кафедра ФМИ График предсказательностей. Программа Diag. Stat. xls • Чем более выгнута красная кривая для PPV, тем лучше способность положительных результатов теста предсказывать наличие болезни. • Чем более выгнута синяя кривая для (1 – NPV), тем лучше способность отрицательных результатов теста предсказывать отсутствие болезни. 107
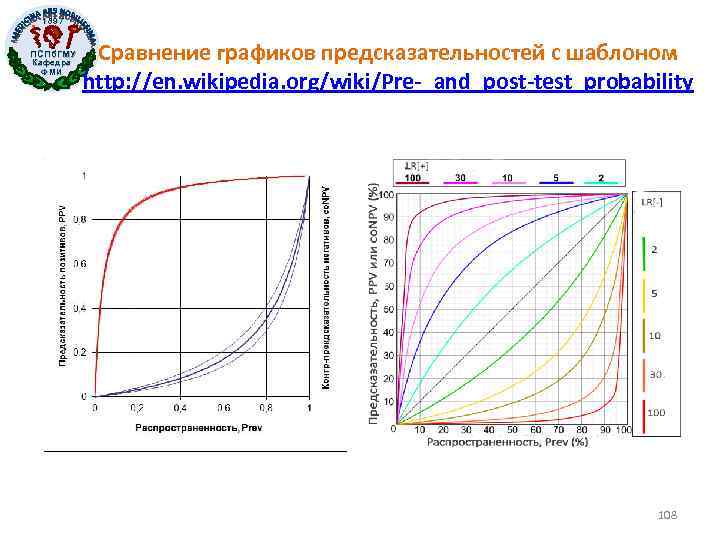
1897 ПСПб. ГМУ Кафедра ФМИ Сравнение графиков предсказательностей с шаблоном http: //en. wikipedia. org/wiki/Pre-_and_post-test_probability 108

1897 ПСПб. ГМУ Кафедра ФМИ Другой способ визуализации качества и информативности проверяемого теста – номограмма Фейгана 109
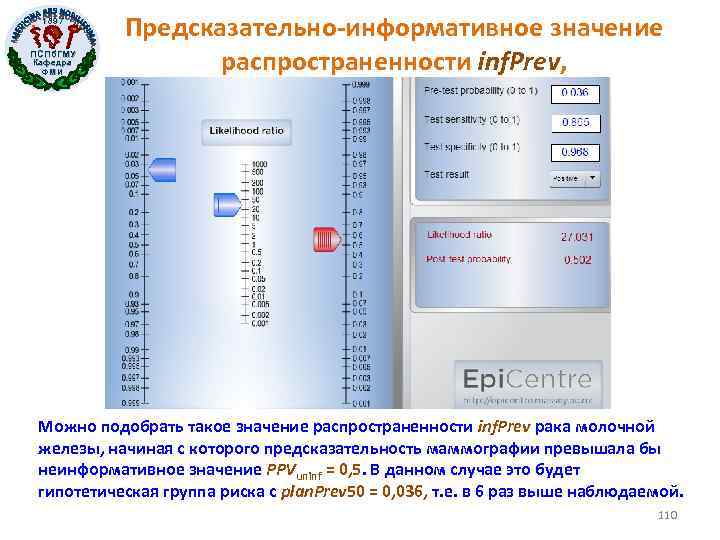
1897 ПСПб. ГМУ Кафедра ФМИ Предсказательно-информативное значение распространенности inf. Prev, Можно подобрать такое значение распространенности inf. Prev рака молочной железы, начиная с которого предсказательность маммографии превышала бы неинформативное значение PPVuninf = 0, 5. В данном случае это будет гипотетическая группа риска с plan. Prev 50 = 0, 036, т. е. в 6 раз выше наблюдаемой. 110
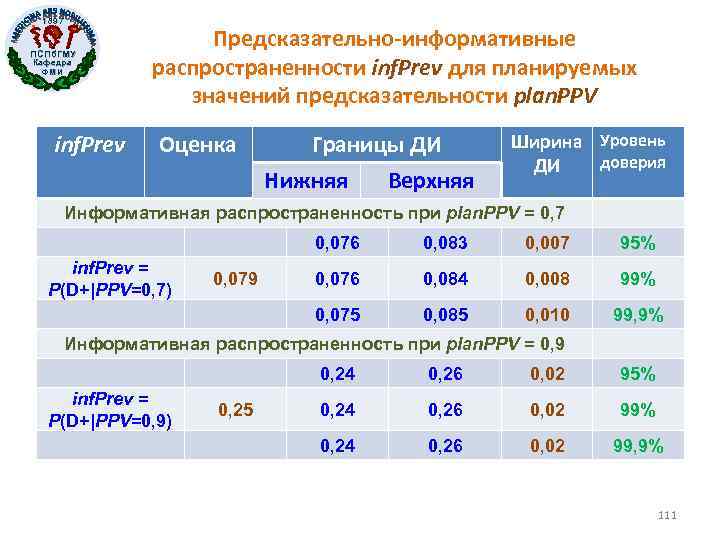
1897 ПСПб. ГМУ Кафедра ФМИ inf. Prev Предсказательно-информативные распространенности inf. Prev для планируемых значений предсказательности plan. PPV Оценка Границы ДИ Нижняя Верхняя Ширина Уровень доверия ДИ Информативная распространенность при plan. PPV = 0, 7 0, 076 0, 079 0, 007 95% 0, 076 0, 084 0, 008 99% 0, 075 inf. Prev = P(D+|PPV=0, 7) 0, 083 0, 085 0, 010 99, 9% Информативная распространенность при plan. PPV = 0, 9 0, 24 inf. Prev = P(D+|PPV=0, 9) 0, 25 0, 26 0, 02 95% 0, 24 0, 26 0, 02 99, 9% 111

Воспроизводимость результатов маммографии 112
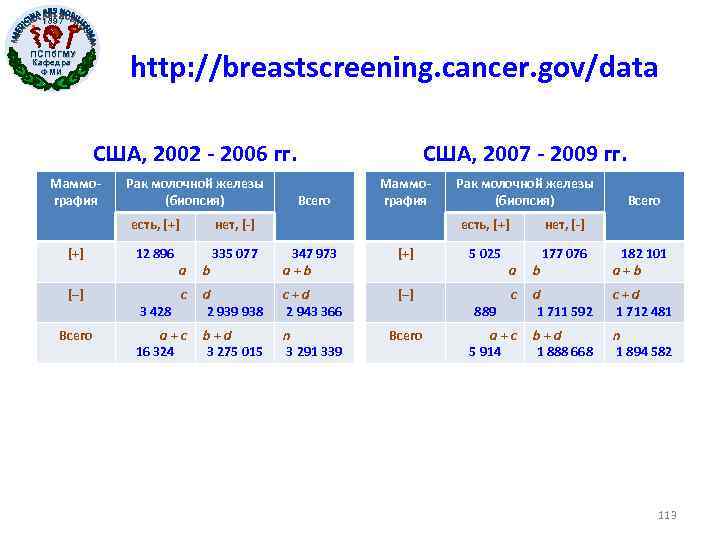
1897 http: //breastscreening. cancer. gov/data ПСПб. ГМУ Кафедра ФМИ США, 2002 - 2006 гг. Маммография Рак молочной железы (биопсия) есть, [+] 12 896 335 077 [−] Всего Маммография нет, [-] [+] США, 2007 - 2009 гг. Всего есть, [+] 347 973 a + b [+] с d 3 428 2 939 938 с + d 2 943 366 [−] a + с 16 324 n 3 291 339 Всего a b b + d 3 275 015 Рак молочной железы (биопсия) нет, [-] 5 025 177 076 Всего 889 a b с d 1 711 592 a + с 5 914 b + d 1 888 668 182 101 a + b с + d 1 712 481 n 1 894 582 113
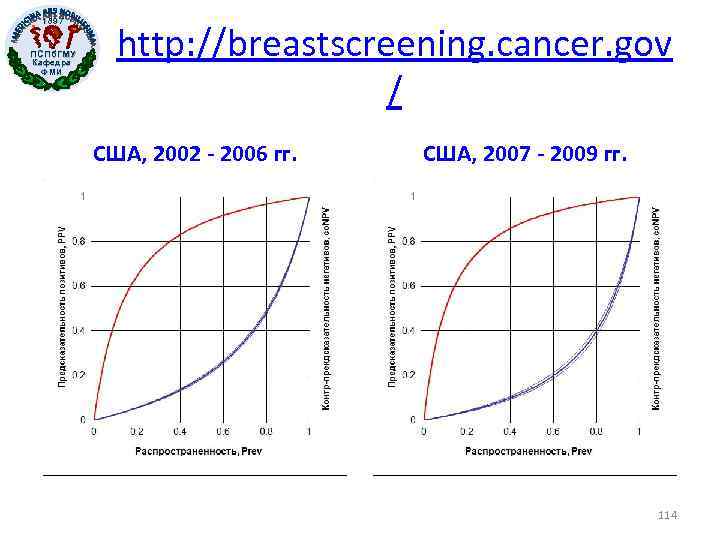
1897 ПСПб. ГМУ Кафедра ФМИ http: //breastscreening. cancer. gov / США, 2002 - 2006 гг. США, 2007 - 2009 гг. 114

Двухвыборочное исследование по по схеме «случаи – контроли» 115

1897 ПСПб. ГМУ Кафедра ФМИ Что такое исследование типа «случаи – контроли» ? • При формировании выборок по схеме «случаи – контроли» случайным образом отбираются две независимые группы субъектов: • - группа субъектов с болезнью – «случаи» и • - группа субъектов без болезни – «контроли» • Такие исследования менее затратны, чем одновыборочные. • Но для них необходимо иметь оценки распространенности заболевания, которые так или иначе получаются на основе одновыборочных иследований. 116

1897 ПСПб. ГМУ Кафедра ФМИ Целиакия • Целиакия — нарушение пищеварения, которое вызывается некоторыми пищевыми продуктами, содержащими определённые белки —глютен (клейковина) и близкие к нему белки (авенин, гордеин и др. ) в таких злаках, как пшеница, рожь, ячмень и овёс. • У некоторых субъектов, предрасположенных к целиакии, эти белки приводят к повреждению ворсинок тонкой кишки. • Болезнь имеет смешанный аутоиммунный, аллергический, наследственный генез, наследуется по аутосомнодоминантному типу. • Синонимы: болезнь Ги — Гертера — Гейбнера, глютенэнтеропатия, кишечный инфантилизм (англ. : Coeliac disease, non-tropical sprue, c(o)eliac sprue, gluten enteropathy and gluten intolerance). 117

1897 ПСПб. ГМУ Кафедра ФМИ Слизистая оболочка тонкой кишки на разрезе • Внутренняя поверхность тонкого кишечника покрыта мелкими ворсинами, благодаря которым площадь всасывания увеличивается. 118
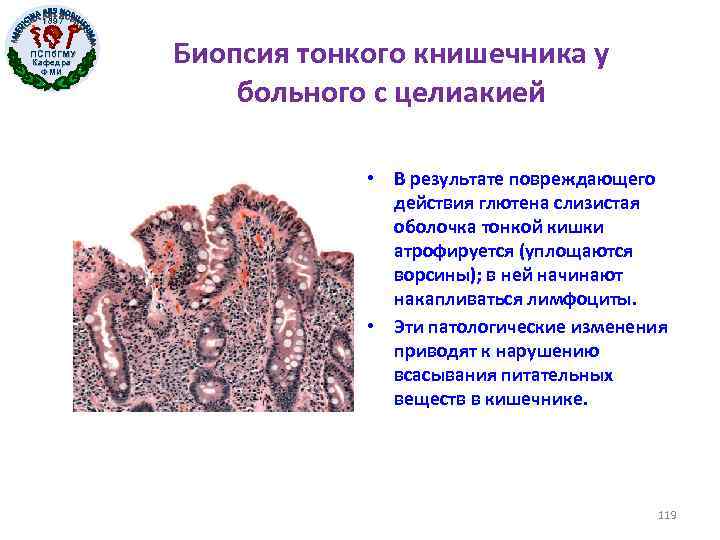
1897 ПСПб. ГМУ Кафедра ФМИ Биопсия тонкого книшечника у больного с целиакией • В результате повреждающего действия глютена слизистая оболочка тонкой кишки атрофируется (уплощаются ворсины); в ней начинают накапливаться лимфоциты. • Эти патологические изменения приводят к нарушению всасывания питательных веществ в кишечнике. 119

1897 ПСПб. ГМУ Кафедра ФМИ Продукты, употребление которых при целиакии исключено 120

1897 ПСПб. ГМУ Кафедра ФМИ Вохмянина Н. В. Опыт HLA-генотипирования больных целиакией. Диагностическая значимость HLA-DQ 2 и HLA-DQ 8. // Медицинская генетика, 2010. - Том 9, N 7. - С. 33 -41. Численности и частоты гаплотипов в группах Всего Гаплотипы Больные целиакией IIIV степени Контрольная группа Предрасполагающие: DQ 2 + DQ 8 191 Se = 0, 860, 920, 95 173 co. Sp = 0, 420, 440, 47 364 Остальные 17 co. Se = 0, 0460, 0820, 14 219 Sp = 0, 530, 560, 58 236 Всего 208 392 600 121

Теорема Бейза в действии 122
![1897 ПСПб. ГМУ Кафедра ФМИ Reverend Thomas Bayes [bɛi: z]) – Преподобный Томас Бейз 1897 ПСПб. ГМУ Кафедра ФМИ Reverend Thomas Bayes [bɛi: z]) – Преподобный Томас Бейз](https://present5.com/presentation/169138935_270038456/image-123.jpg)
1897 ПСПб. ГМУ Кафедра ФМИ Reverend Thomas Bayes [bɛi: z]) – Преподобный Томас Бейз (Байес, Бейес) c. 1702 – 17. 04. 1761 Теорема Бейза 123

1897 ПСПб. ГМУ Кафедра ФМИ Предсказательность позитива PPV и негатива NPV в двухвыборочном исcледовании • В общем виде согласно теореме Бейза 124

1897 ПСПб. ГМУ Кафедра ФМИ Распространенность целиакии • Долгое время целиакия считалась редким заболеванием с распространенностью от 1 : 10 000 до 1 : 1000. • Однако по современным данным она считается довольно распространенным заболеванием. • В США и в Европе (в России в частности) распространенность целиакии варьирует от 1: 300 до 1: 100, т. е. от 0, 3% до 1%. • Средняя распространенность целиакии в мире оценивается как 1 : 184, т. е. 0, 54%. 125

1897 ПСПб. ГМУ Кафедра ФМИ Сравнение диагностической и прогностической способностей маммографии и HLA-гаплотипирования • Мамография и рак молочной железы • Se = 0, 830, 870, 90 • Sp = 0, 9670, 9680, 969 • LR[+] = 252729 • LR[-] = 0, 110, 140, 17 • f(D+) = 0, 00540, 00590, 0065 • PPV = 0, 1260, 1390, 153 • NPV = 0, 99890, 99920, 9994 • HLA-гаплотипирование и целиакия • Se = 0, 860, 920, 95 • Sp = 0, 530, 560, 58 • LR[+] = 1, 82, 12, 3 • LR[-] = 0, 080, 150, 26 • «Внешние данные» : • f(D+) = 0, 0054 • Размах: от 0, 0033 до 0, 010 • PPV = 0, 0070, 0110, 18 • NPV = 0, 99820, 9996 126
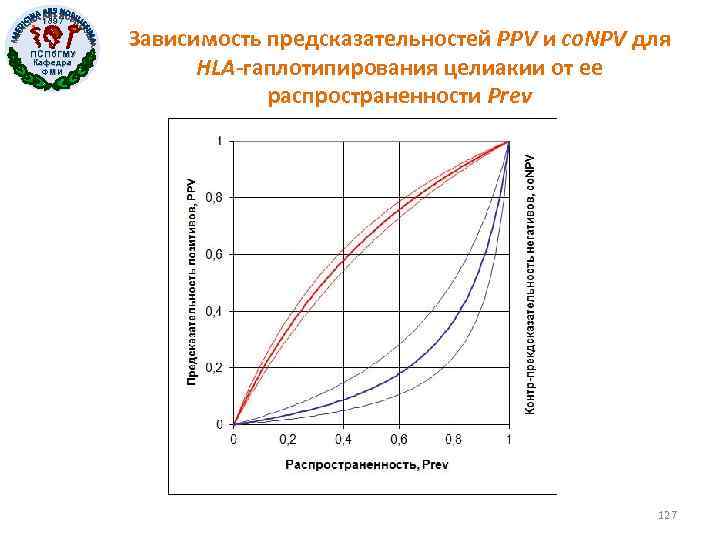
1897 ПСПб. ГМУ Кафедра ФМИ Зависимость предсказательностей PPV и co. NPV для HLA-гаплотипирования целиакии от ее распространенности Prev 127
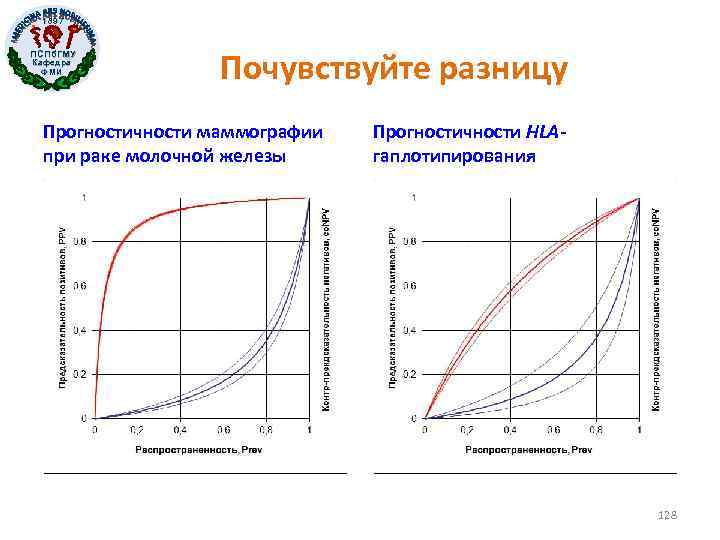
1897 ПСПб. ГМУ Кафедра ФМИ Почувствуйте разницу Прогностичности маммографии при раке молочной железы Прогностичности HLAгаплотипирования 128

Воспроизводимость результатов применения HLAгаплотипирования для диагностики целиакии 129

1897 ПСПб. ГМУ Кафедра ФМИ Вохмянина Н. В. Опыт HLA-генотипирования больных целиакией. Диагностическая значимость HLA-DQ 2 и HLA-DQ 8. // Медицинская генетика, 2010. - Том 9, N 7. - С. 33 -41. Mäki M. , Mustalahti K. , Kokkonen J. , Kulmala P. , Haapalahti M. , Karttunen T. , Ilonen J. , Laurila K. , Dahlbom I. , Hansson T. , Höpfl P. , Knip M. Prevalence of celiac disease among children in Finland. N. Engl. J. Med. – 2003. Vol. 348. – P. 2517 -2524. Численности и частоты гаплотипов в группах Больные целиа-кией II-IV степени Контрольная группа Всего DQ 2 + DQ 8 191 173 364 Остальные 17 219 236 Всего 208 392 600 Гаплотипы Тест на аутоантитела Гаплотипы Положительный Отрицательный Всего DQ 2+DQ 8 54 1357 1465 Остальные 2 2214 2216 Всего 56 3571 3627 130
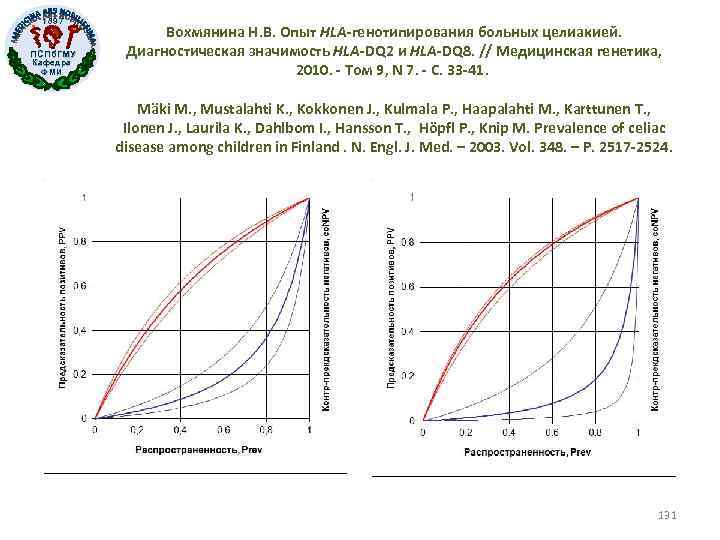
1897 ПСПб. ГМУ Кафедра ФМИ Вохмянина Н. В. Опыт HLA-генотипирования больных целиакией. Диагностическая значимость HLA-DQ 2 и HLA-DQ 8. // Медицинская генетика, 2010. - Том 9, N 7. - С. 33 -41. Mäki M. , Mustalahti K. , Kokkonen J. , Kulmala P. , Haapalahti M. , Karttunen T. , Ilonen J. , Laurila K. , Dahlbom I. , Hansson T. , Höpfl P. , Knip M. Prevalence of celiac disease among children in Finland. N. Engl. J. Med. – 2003. Vol. 348. – P. 2517 -2524. 131

Галерея графиков предсказательностей 132
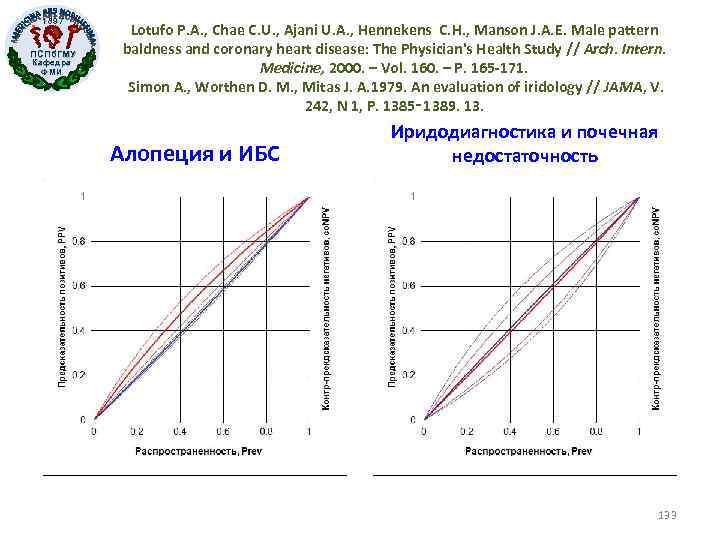
1897 ПСПб. ГМУ Кафедра ФМИ Lotufo P. A. , Chae C. U. , Ajani U. A. , Hennekens C. H. , Manson J. A. E. Male pattern baldness and coronary heart disease: The Physician's Health Study // Arch. Intern. Medicine, 2000. – Vol. 160. – P. 165 -171. Simon A. , Worthen D. M. , Mitas J. A. 1979. An evaluation of iridology // JAMA, V. 242, N 1, P. 1385‑ 1389. 13. Алопеция и ИБС Иридодиагностика и почечная недостаточность 133
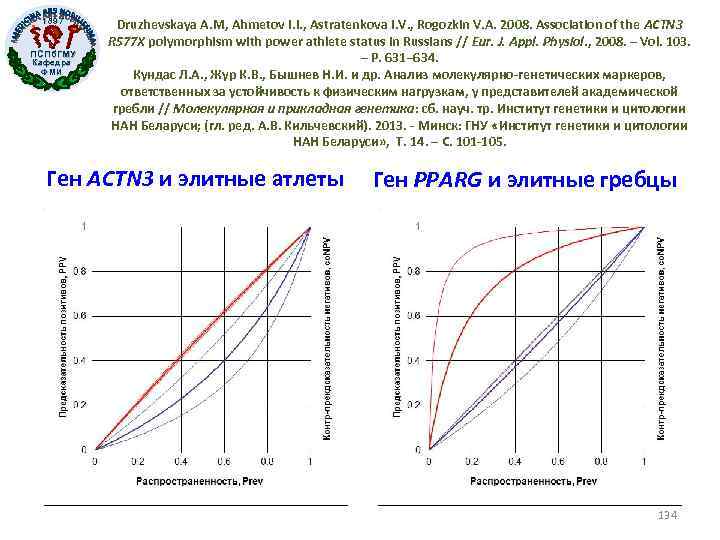
1897 ПСПб. ГМУ Кафедра ФМИ Druzhevskaya A. M, Ahmetov I. I. , Astratenkova I. V. , Rogozkin V. A. 2008. Association of the ACTN 3 R 577 X polymorphism with power athlete status in Russians // Eur. J. Appl. Physiol. , 2008. – Vol. 103. – P. 631– 634. Кундас Л. А. , Жур К. В. , Бышнев Н. И. и др. Анализ молекулярно-генетических маркеров, ответственных за устойчивость к физическим нагрузкам, у представителей академической гребли // Молекулярная и прикладная генетика: сб. науч. тр. Институт генетики и цитологии НАН Беларуси; (гл. ред. А. В. Кильчевский). 2013. - Минск: ГНУ «Институт генетики и цитологии НАН Беларуси» , Т. 14. – C. 101 -105. Ген ACTN 3 и элитные атлеты Ген PPARG и элитные гребцы 134
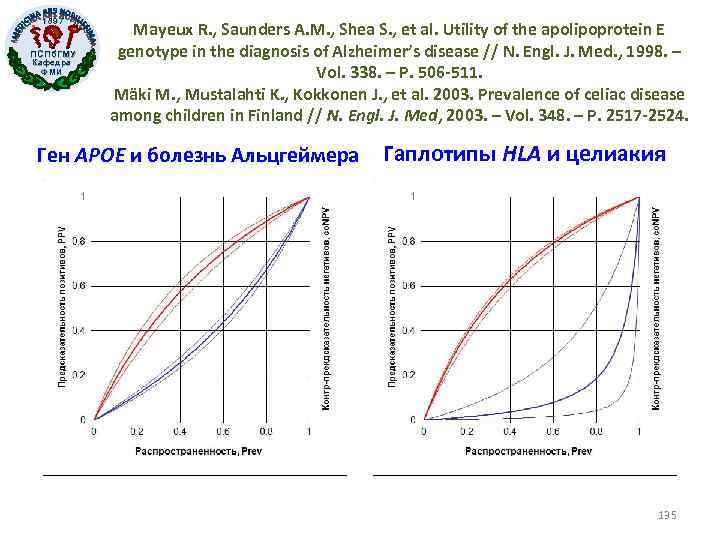
1897 ПСПб. ГМУ Кафедра ФМИ Mayeux R. , Saunders A. M. , Shea S. , et al. Utility of the apolipoprotein E genotype in the diagnosis of Alzheimer’s disease // N. Engl. J. Med. , 1998. – Vol. 338. – P. 506 -511. Mäki M. , Mustalahti K. , Kokkonen J. , et al. 2003. Prevalence of celiac disease among children in Finland // N. Engl. J. Med, 2003. – Vol. 348. – P. 2517 -2524. Ген APOE и болезнь Альцгеймера Гаплотипы HLA и целиакия 135
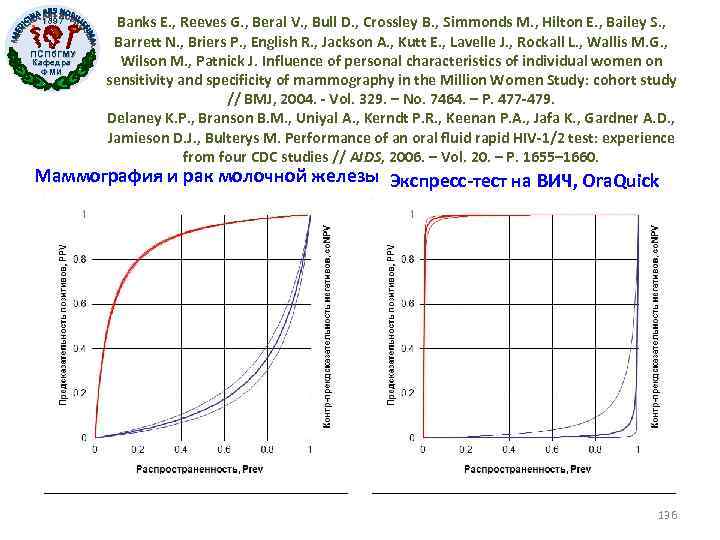
1897 ПСПб. ГМУ Кафедра ФМИ Banks E. , Reeves G. , Beral V. , Bull D. , Crossley B. , Simmonds M. , Hilton E. , Bailey S. , Barrett N. , Briers P. , English R. , Jackson A. , Kutt E. , Lavelle J. , Rockall L. , Wallis M. G. , Wilson M. , Patnick J. Influence of personal characteristics of individual women on sensitivity and specificity of mammography in the Million Women Study: cohort study // BMJ, 2004. - Vol. 329. – No. 7464. – P. 477 -479. Delaney K. P. , Branson B. M. , Uniyal A. , Kerndt P. R. , Keenan P. A. , Jafa K. , Gardner A. D. , Jamieson D. J. , Bulterys M. Performance of an oral fluid rapid HIV-1/2 test: experience from four CDC studies // AIDS, 2006. – Vol. 20. – P. 1655– 1660. Маммография и рак молочной железы Экспресс-тест на ВИЧ, Ora. Quick 136

1897 ПСПб. ГМУ Кафедра ФМИ И снова теорема Бейза: Как комбинировать две независимые PPV? 137

1897 ПСПб. ГМУ Кафедра ФМИ PPV 1, 2 для двух независимых тестов • Предположим, что в дополнение к маммографическому обследованию (тест Т 1) с PPV 1 = 0, 14 проведено дополнительное независимое диагностическое исследование (тест T 2) с такими же чувствительностью и специфичностью: Se 2 = 0, 87 и Sp 2 = 0, 97. • Тогда получаем: PPV 1, 2=(0, 006 0, 87): (0, 006 0, 87+0, 9 94 0, 03) = 0, 83 ! 138

1897 ПСПб. ГМУ Кафедра ФМИ PPV 1, 2 для двух независимых тестов • Предположим, что в дополнение к HLAгаплотипированию (тест Т 1) с PPV 1 = 0, 011 проведен независимое диагностическое исследование (тест T 2) с такими же чувствительностью и специфичностью: Se 2 = 0, 92 и Sp 2 = 0, 56. • Тогда получаем: PPV 1, 2=(0, 054 0, 92): (0, 054 0, 92+ • +0, 946 0, 44) = 0, 20 ! 139

Указания к практическому занятию 140

1897 ПСПб. ГМУ Кафедра ФМИ • • • Изложите своими словами суть предложенного задания. Что выбрано в качестве золотого стандарта или эталона сравнения? Согласны ли Вы с его выбором? Какой диагностический тест сравнивается с эталонным? В чем его предполагаемое преимущество перед эталонным тестом? Является ли исследование одновыборочным или двух выборочным? Если исследование одновыборочное, то каков объем изученной выборки? Сколько выявлено субъектов с болезнью? Сколько из них выявлено истинных позитивов и сколько ложных негативов? Сколько выявлено субъектов без болезнью? Сколько из них выявлено истинных негативов сколько ложных позитивов? 141

1897 ПСПб. ГМУ Кафедра ФМИ • Какую компьютерную программу Вы будете использовать для статистического контроля качества предлагаемого диагностического теста? • Если исследование одновыборочное, то какую подпрограмму Вы буте использовать? • Какие вероятностные показатели распознавательной способности Вы будете оценивать? • Какие вероятностные показатели предсказательной способности Вы будете оценивать? • Объясните своими словами суть вычисляемых точечных и интервальных оценок всех этих показателей. • Объясните смысл доверительных вероятностей (уровней доверия) и представленных в программе их трех их значений. • Какой показатель Вы используете для оценки точности получаемых интервальных оценок всех этих показателей? 142

1897 ПСПб. ГМУ Кафедра ФМИ • Какие значения показателей распознавательной способности ПДТ следует признать неинформативными и каково их назначение? • Оцените статистическую значимость полученных оценок. • Изложите ход рассуждений об их статистической значимости. • Используя вербальную шкалу, охарактеризуйте словесно практическую ценность полученных оценок показателей распознавательной способности ПДТ. • Какие значения показателей предсказательной способности ПДТ следует признать неинформативными и каково их назначение? • Оцените статистическую значимость полученных оценок. • Изложите ход рассуждений об их статистической значимости. • Используя вербальную шкалу, охарактеризуйте словесно практическую ценность полученных оценок показателей предсказателей способности ПДТ. 143

1897 ПСПб. ГМУ Кафедра ФМИ • Изложите словами суть таких показателей как отношения правдоподобий в терминах распознавательной способности ПДТ и в терминах отношения оддов (шансов за/против). • Какие значения отношения правдоподобий следует признать неинформативными и каково их назначение? • Оцените статистическую значимость полученных оценок. • Изложите ход рассуждений об их статистической значимости. • Используя вербальную шкалу, охарактеризуйте словесно практическую ценность полученных оценок отношений правдоподобий. • Какие программы Вы будете использовать для графического представления полученных результатов? • Постройте графики предсказательностей и сопоставьте их с прилагаемым шаблоном. 144

1897 ПСПб. ГМУ Кафедра ФМИ • На основе полученных графиков предсказательностей изложите свое мнение о качестве проверяемого диагностического теста. • При этом обратите внимание на ширину доверительных интервалов (доверительных зон) на этих графиках и сформулируйте выводы о точности оценок предсказательности позитивов и предсказательности негативов. • Используя номограмму Фейгена, найдите то значение распространенности болезни, начиная с которого предсказательность позитивов начнет превышать свое неинформативное значение. 145

1897 ПСПб. ГМУ Кафедра ФМИ Повторности и воспроизводимость • Если кому-то из Ваших коллег предложено аналогичное задание: диагностируется та же болезнь и сравниваются тот же эталон сравнения и проверяемый тест, то совместно с ними обсудите воспроизводимость результатов. 146

1897 ПСПб. ГМУ Кафедра ФМИ ГОСТ Р 53022. 3 -2008 • Настоящий стандарт устанавливает единые правила оценки клинической информативности лабораторных исследований, выполняемых в клиникодиагностических лабораториях медицинских организаций в целях оценки состояния здоровья, клинической диагностики и слежения за эффективностью лечения пациентов. 147

1897 ПСПб. ГМУ Кафедра ФМИ • Тишков А. В. , Хромов. Борисов Н. Н. , Комашня А. В. , и др. Статистический анализ таблиц в диагностических исследованиях, 2013. – СПб. : Изд-во СПб. ГМУ, 20 с. 148

1897 ПСПб. ГМУ Кафедра ФМИ 149

Домашнее задание: освежаем в памяти элементы теории вероятностей Задачи и упражнения 150

1897 ПСПб. ГМУ Кафедра ФМИ Льюис Кэрролл (Lewis Carroll, настоящее имя Чарльз Лютвидж Доджсон, Charles Lutwidge Dodgson; 27. 01. 1832 – 14. 01. 1898) 151

1897 ПСПб. ГМУ Кафедра ФМИ 152

1897 ПСПб. ГМУ Кафедра ФМИ Полуночные задачи (задача № 5) • В мешке находится шар, о котором известно, что с вероятностью равной 1/2 он либо белый, либо черный. • В этот мешок кладут белый шар, после чего содержимое мешка тщательно перемешивают, и человек наугад извлекает один шар, который оказывается белым. • Вопрос: какова после этого вероятность извлечь белый шар? 153

1897 ПСПб. ГМУ Кафедра ФМИ Задача о картировании генов На одной хромосоме расположены три гена A, B и С. Известны: - PAB - вероятность кроссинговера на участке между генами A и B и • - PBC - вероятность кроссинговера на участке между генами B и C. • По формуле Троу вероятность кроссинговера на участке между генами A и C есть: • PAC = PAB + PBC - 2 PABPBC • Выведите эту формулу самостоятельно. • • 154

1897 ПСПб. ГМУ Кафедра ФМИ • • • После продолжительной разлуки встречаются два приятеля. Между ними происходит следующий диалог: - Ну, как дела? - Да вот уже тремя детьми обзавелся. - А сколько им лет? - Произведение их возрастов равно 36, а сумма их возрастов равна номеру проезжающего трамвая. После некоторого раздумья второй приятель говорит: - По-моему, ты чего-то не договариваешь. - Ах, да – я забыл сказать, что старший у меня рыжий. Вопрос: сколько лет детям? 155

1897 «Подножный» материал к последующим практическим занятиям 1. ЧСС – частота сердечных сокращений ровно за 60 секунд (не за 15!) 2. САД – систолическое артериальное давление (мм Hg) 3. ДАД – диастолическое артериальное давление (мм Hg) 4. Рост (см) 5. Масса тела (кг) 6. Пол ПСПб. ГМУ Кафедра ФМИ • • • 156
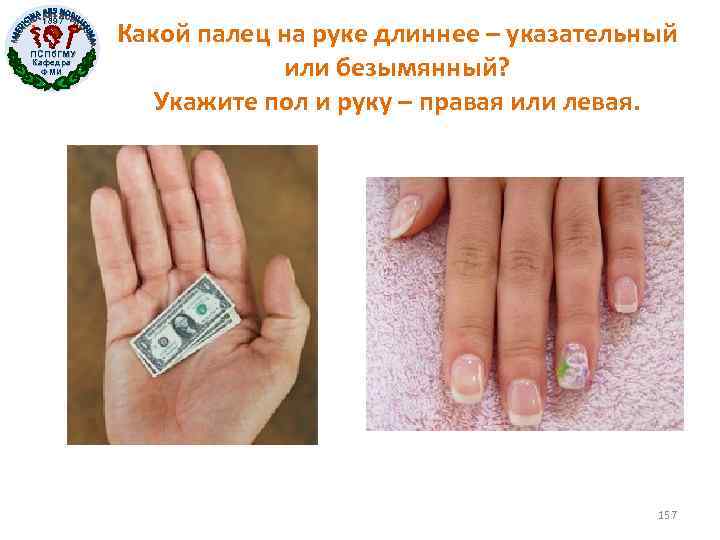
1897 ПСПб. ГМУ Кафедра ФМИ Какой палец на руке длиннее – указательный или безымянный? Укажите пол и руку – правая или левая. 157

1897 ПСПб. ГМУ Кафедра ФМИ Высыпите на стол коробок канцелярских кнопок и подсчитайте, сколько из них лягут на шляпку острием вверх, а сколько – на острие и шляпку. 158

1897 ПСПб. ГМУ Кафедра ФМИ Признательность • Благодарю весь славный коллектив Кафедры ФМИ за помощь в работе. 159

Спасибо за внимание! Слайды доступны для всех Никита Николаевич Хромов-Борисов Кафедра физики, математики и информатики ПСПб. ГМУ им. акад. И. П. Павлова Nikita. Khromov. Borisov@gmail. com 8 -952 -204 -89 -49 – моб. 160
Лекция 1_10_02_2014.ppt