медианы Тема:

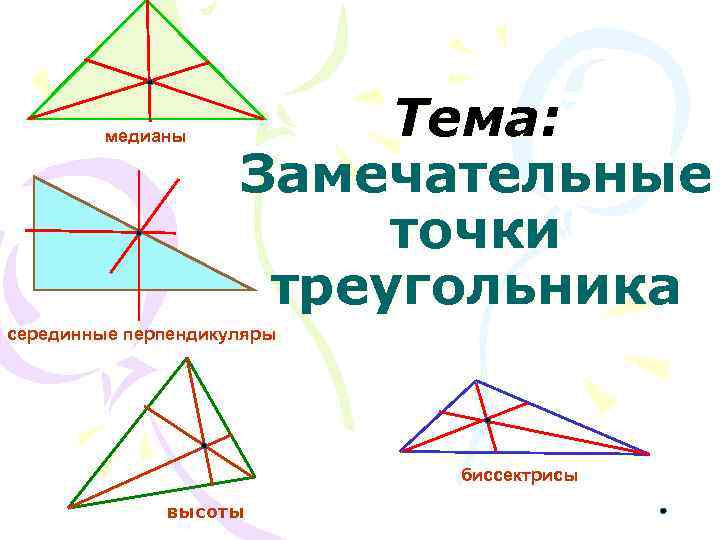
медианы Тема: Замечательные точки треугольника серединные перпендикуляры биссектрисы высоты

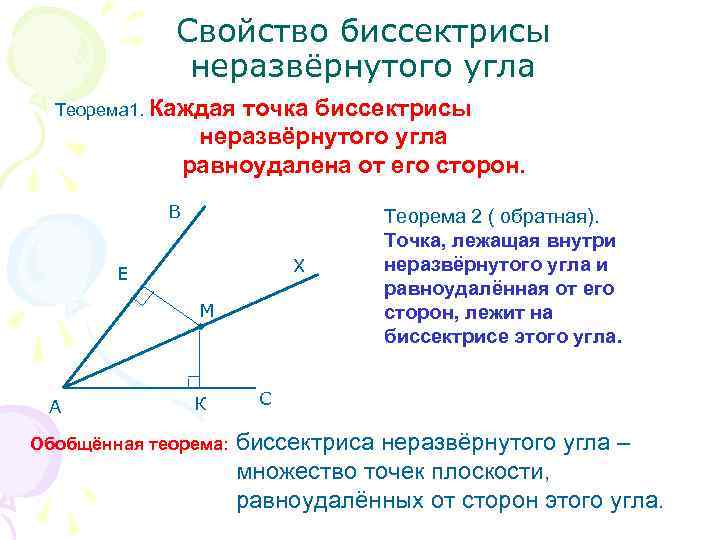
Свойство биссектрисы неразвёрнутого угла Теорема 1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. В Теорема 2 ( обратная). Точка, лежащая внутри Е Х неразвёрнутого угла и равноудалённая от его М сторон, лежит на биссектрисе этого угла. А К С Обобщённая теорема: биссектриса неразвёрнутого угла – множество точек плоскости, равноудалённых от сторон этого угла.

Серединный перпендикуляр к отрезку Теорема 1. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. Р М Теорема 2. Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. А К В Обобщённая теорема: серединный перпендикуляр к отрезку – множество точек плоскости, равноудалённых от его концов.

Четыре замечательные точки

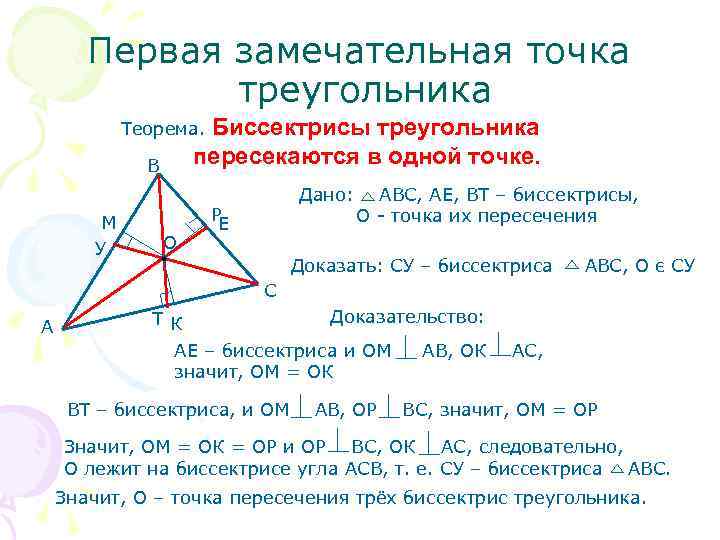
Первая замечательная точка треугольника Теорема. Биссектрисы треугольника В пересекаются в одной точке. Дано: АВС, АЕ, ВТ – биссектрисы, М Р О - точка их пересечения Е У О Доказать: СУ – биссектриса АВС, О є СУ С Т К Доказательство: А АЕ – биссектриса и ОМ АВ, ОК АС, значит, ОМ = ОК ВТ – биссектриса, и ОМ АВ, ОР ВС, значит, ОМ = ОP Значит, ОМ = ОК = ОР и ОР ВС, ОК АС, следовательно, О лежит на биссектрисе угла АСВ, т. е. СУ – биссектриса АВС. Значит, О – точка пересечения трёх биссектрис треугольника.

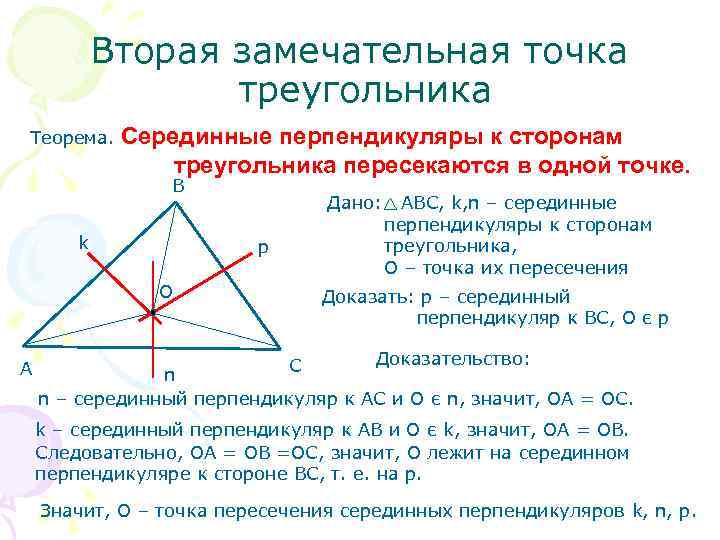
Вторая замечательная точка треугольника Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. В Дано: АВС, k, n – серединные перпендикуляры к сторонам k p треугольника, О – точка их пересечения О Доказать: р – серединный перпендикуляр к ВС, О є р С Доказательство: А n n – серединный перпендикуляр к АС и О є n, значит, ОА = ОС. k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ. Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном перпендикуляре к стороне ВС, т. е. на р. Значит, О – точка пересечения серединных перпендикуляров k, n, p.

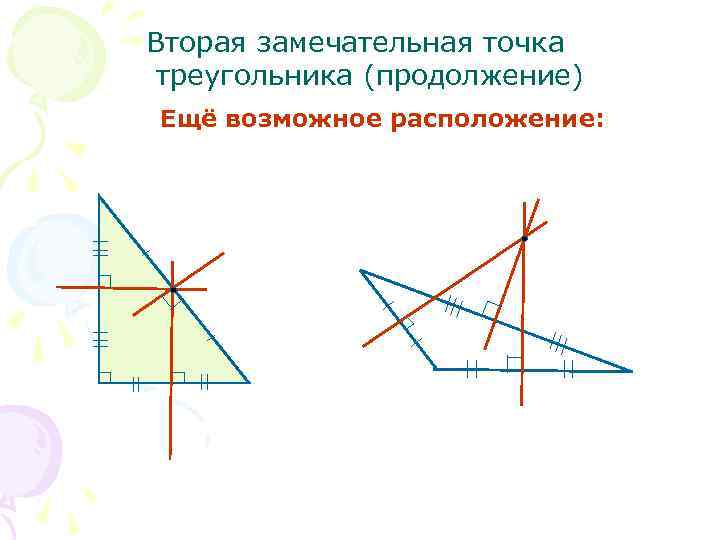
Вторая замечательная точка треугольника (продолжение) Ещё возможное расположение:

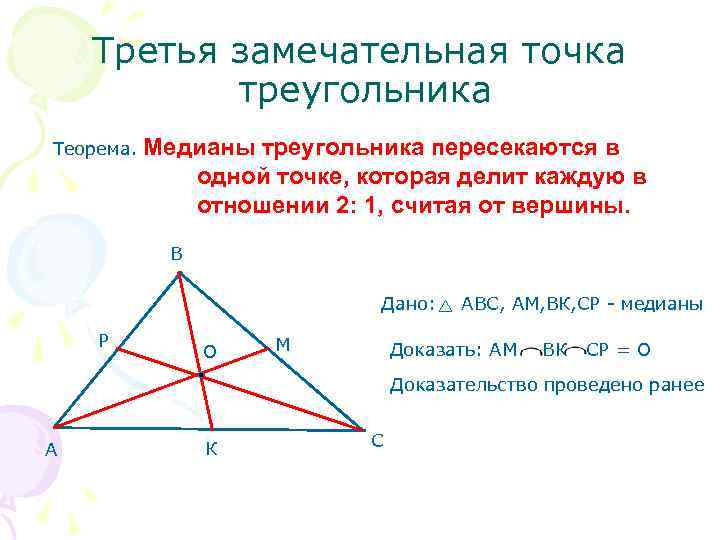
Третья замечательная точка треугольника Теорема. Медианы треугольника пересекаются в одной точке, которая делит каждую в отношении 2: 1, считая от вершины. В Дано: АВС, AM, ВК, СР - медианы Р М Доказать: АМ ВК СР = О Доказательство проведено ранее А К С

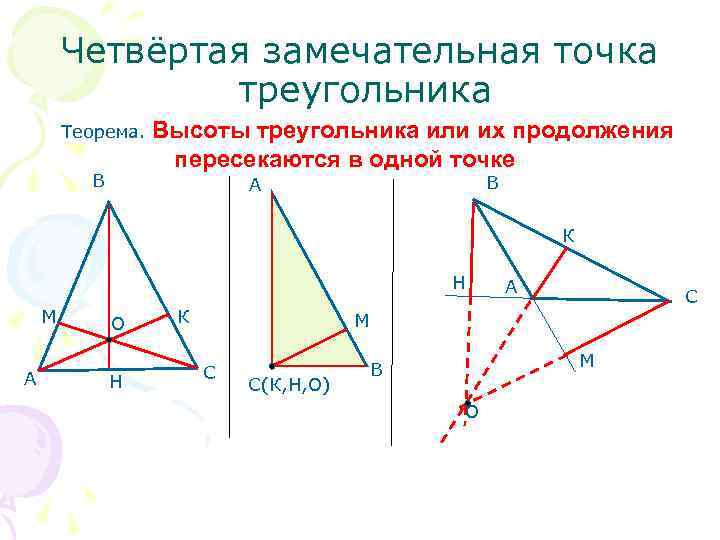
Четвёртая замечательная точка треугольника Теорема. Высоты треугольника или их продолжения пересекаются в одной точке В А В К Н А С М О К М М А С В Н С(К, Н, О) О

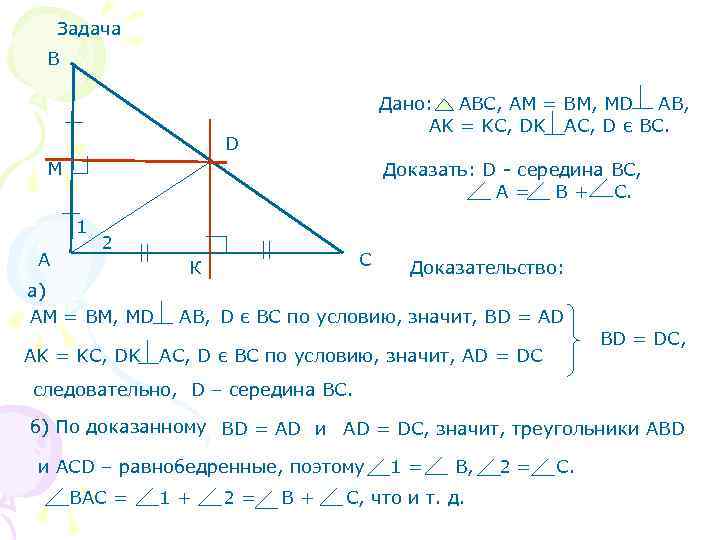
Задача В Дано: АВС, АМ = ВМ, МD AB, AK = KC, DK AC, D є BC. D М Доказать: D - середина ВС, А = В + С. 1 2 А К С Доказательство: а) АМ = ВМ, МD AB, D є BC по условию, значит, ВD = AD BD = DC, AK = KC, DK AC, D є BC по условию, значит, AD = DC следовательно, D – середина ВС. б) По доказанному ВD = AD и AD = DC, значит, треугольники АВD и АСD – равнобедренные, поэтому 1= В, 2= С. ВАС = 1+ 2= В+ С, что и т. д.

Домашнее задание: Глава 1 § 1 – 3. Раздел V ст. 204 № 5. 2. 50 (б).