Медианы, биссектрисы и высоты треугольника
Ø медианы треугольника Ø биссектрисы треугольника Ø высоты треугольника
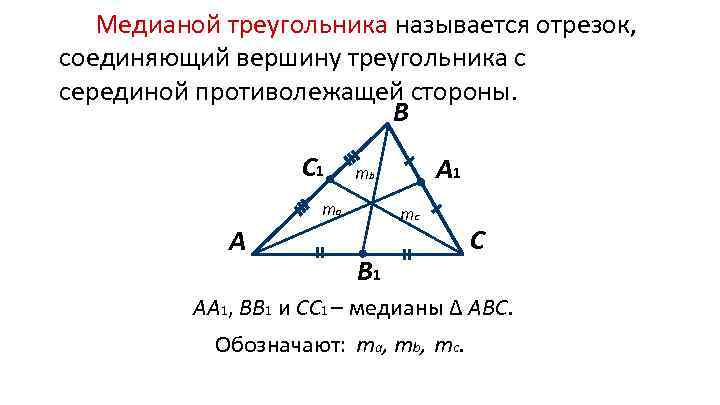
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. В C 1 ma А A 1 mb mc B 1 С АA 1, ВB 1 и СC 1 – медианы ∆ АВС. Обозначают: ma, mb, mc.
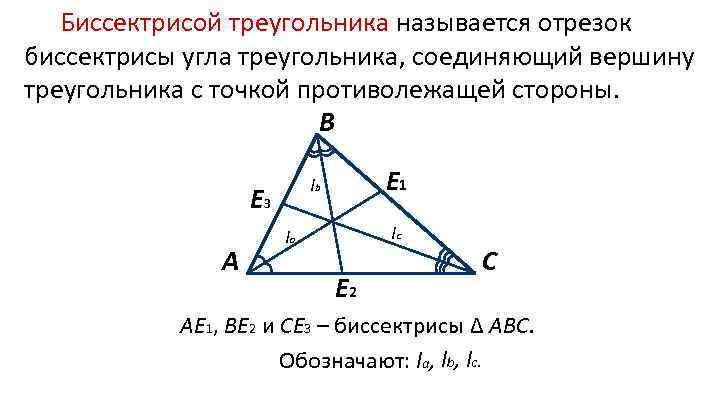
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны. B E 3 А E 1 lb lc la E 2 C АE 1, ВE 2 и СE 3 – биссектрисы ∆ АВС. Обозначают: la, lb, lc.
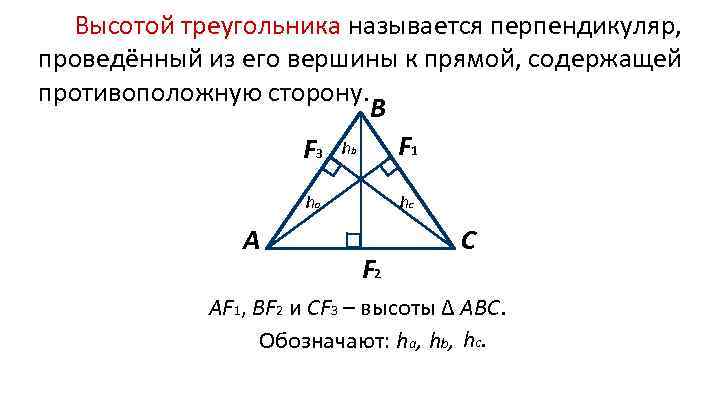
Высотой треугольника называется перпендикуляр, проведённый из его вершины к прямой, содержащей противоположную сторону. В F 1 F 3 h b ha А hc F 2 С АF 1, ВF 2 и СF 3 – высоты ∆ АВС. Обозначают: ha, hb, hc.
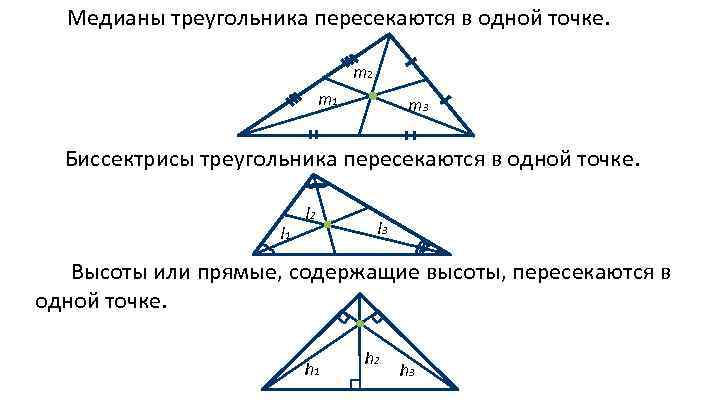
Медианы треугольника пересекаются в одной точке. m 2 m 1 m 3 Биссектрисы треугольника пересекаются в одной точке. l 1 l 2 l 3 Высоты или прямые, содержащие высоты, пересекаются в одной точке. h 1 h 2 h 3
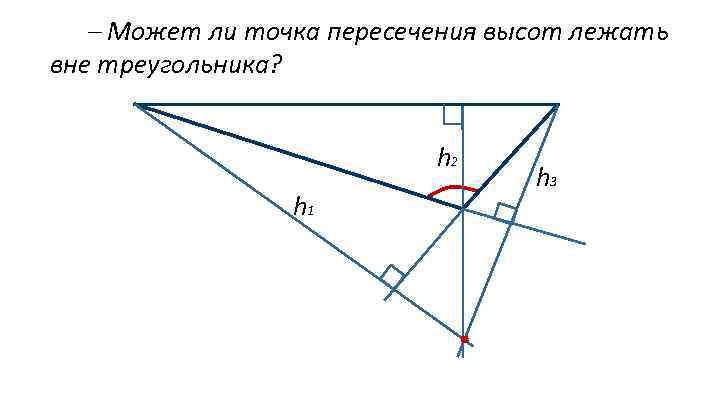
Может ли точка пересечения высот лежать вне треугольника? h 2 h 1 h 3
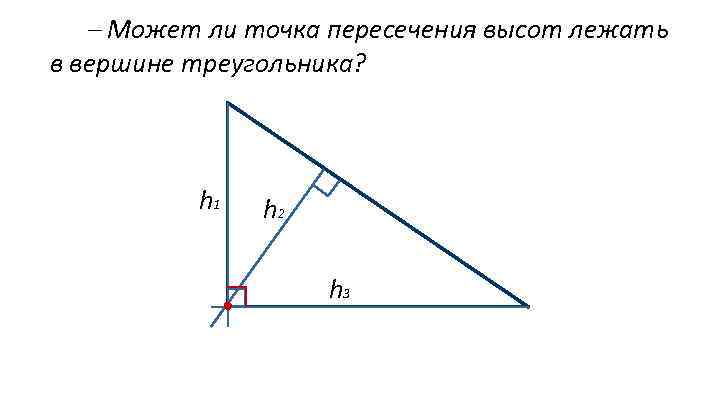
Может ли точка пересечения высот лежать в вершине треугольника? h 1 h 2 h 3
Задача. Отрезок BD – медиана треугольника АВС, отрезок ВЕ – медиана треугольника DBC. Чему равна длина отрезка АС, если отрезок ЕС равен 4 сантиметра? Решение. В Так как ВЕ – медиана ∆ то DE = EC, DВС, следовательно, DС = 2 EC, DС = 2 4 = 8 см. ВD – медиана ∆ AВС, значит AD = DC, А следовательно, AС = 2 DC, AС = 2 8 = 16 см. Ответ: 16 см. D E С
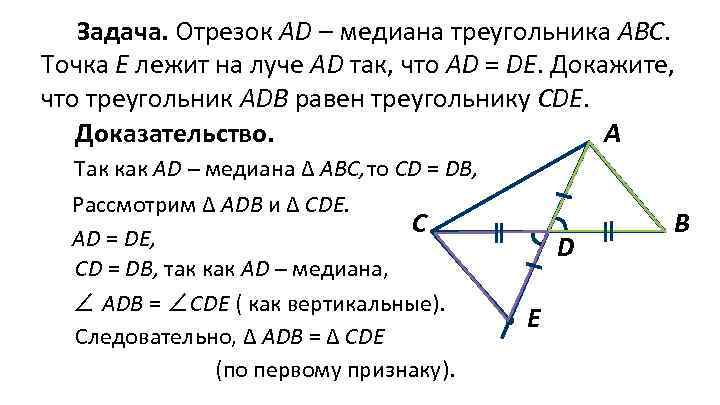
Задача. Отрезок AD – медиана треугольника АВС. Точка Е лежит на луче АD так, что AD = DЕ. Докажите, что треугольник АDВ равен треугольнику CDE. Доказательство. А Так как AD – медиана ∆ AВС, то СD = DB, Рассмотрим ∆ ADB и ∆ СDЕ. С АD = DЕ, СD = DВ, так как AD – медиана, ∠ ADB = ∠CDE ( как вертикальные). Следовательно, ∆ ADB = ∆ СDЕ (по первому признаку). D E В
Скачать презентацию Медианы биссектрисы и высоты треугольника Ø медианы
08. Медианы, биссектрисы и высоты треугольника.pptx