Mechanics of Materials 1 2 CHAPTER

Mechanics of Materials 1

2

CHAPTER 1 AXIAL TENSION AND COMPRESSION § 1– 1 Concepts and practical examples of axial tension and compression § 1– 2 Internal force、method of section、axial force and its diagram § 1– 3 Stresses on the section and strength conditions § 1 -4 Deformation of the rod in axial tension and compression law of elasticity § 1 -5 Elastic strain energy of the rod in axial tension and compression § 1 -6 Statically indeterminate problems and their treatment methods of axial tension and compression § 1 -7 Mechanical properties of materials in axial tension and compression 3

第一章 轴向拉伸和压缩 § 1– 1 轴向拉压的概念及实例 § 1– 2 内力、截面法、轴力及轴力图 § 1– 3 截面上的应力及强度条件 § 1 -4 拉压杆的变形 弹性定律 § 1 -5 拉压杆的弹性应变能 § 1 -6 拉压超静定问题及其处理方法 § 1 -7 材料在拉伸和压缩时的力学性能

§ 1– 1 CONCEPTS AND PRACTICAL EXAMPLES OF AXIAL TENSION AND COMPRESSION 1、Concepts Characteristic of the external force： The acting line of the resultant of external forces is coincided with the axis of the rod. Characteristic of the deformation：Deformation of the rod is mainly elongation or contraction along the axis of the rod and companied with lateral reduction or enlargement. Axial tension ：Deformation of the rod is axial elongation and lateral shortening. Axial compression：Deformation of the rod is axial shortening and lateral enlargement. 5

§ 1– 1 轴向拉压的概念及实例 一、概念 轴向拉压的外力特点：外力的合力作用线与杆的轴线重合。 轴向拉压的变形特点：杆的变形主要是轴向伸缩，伴随横向 缩扩。 轴向拉伸：杆的变形是轴向伸长，横向缩短。 轴向压缩：杆的变形是轴向缩短，横向变粗。

Mechanical models are shown in the figures In axial tension，the corresponding force is called tensile force. In axial compression，the corresponding force is called compressive force. 7

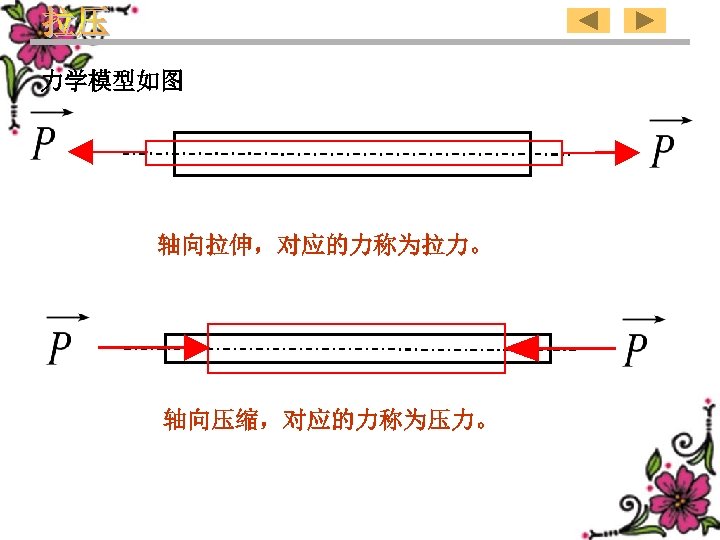力学模型如图 轴向拉伸，对应的力称为拉力。 轴向压缩，对应的力称为压力。

2、 Practical examples in engineering 9

二、 程 实 例

11

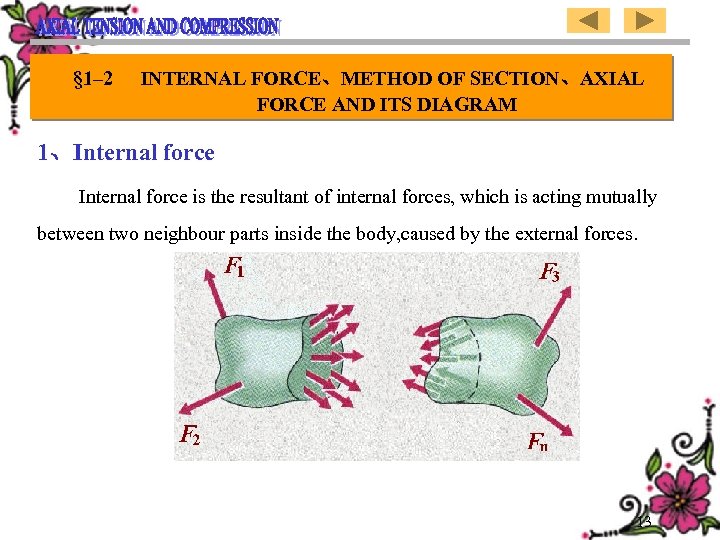§ 1– 2 INTERNAL FORCE、METHOD OF SECTION、AXIAL FORCE AND ITS DIAGRAM 1、Internal force is the resultant of internal forces, which is acting mutually between two neighbour parts inside the body, caused by the external forces. 13

§ 1– 2 内力 · 截面法 · 轴力及轴力图 一、内力 指由外力作用所引起的、物体内相邻部分之间分布内 力系的合成（附加内力）。

2、Method of section · axial force Calculation of the internal forces is the foundation to analyze the problems of strength、rigidity、stability etc. The general method to determine internal forces is the method of section. 1). Basic steps of the method of section： ① Cut off：Assume to separate the rod into two distinct parts in the section in which the internal forces are to be determined. ②Substitute：Take arbitrary part and substitute the action of another part on it by the corresponding internal force in the cut-off section. ③Equilibrium：Set up equilibrium equations for the remained part and determine the unknown internal forces according to the external forces acted on it. （Here the internal forces in the cut-off section are the external forces for the remained part） 15

二、截面法 · 轴力 内力的计算是分析构件强度、刚度、稳定性等问题的 基础。求内力的一般方法是截面法。 1. 截面法的基本步骤： ① 截开：在所求内力的截面处，假想地用截面将杆件一分为二。 ②代替：任取一部分，其弃去部分对留下部分的作用，用作用 在截开面上相应的内力（力或力偶）代替。 ③平衡：对留下的部分建立平衡方程，根据其上的已知外力来 计算杆在截开面上的未知内力（此时截开面上的内力 对所留部分而言是外力）。

Such as： Determine N by the method of section. P Cut off: ： P A P Simple sketch Substitute： P N A Equilibrium： 2. Axial force—internal force of the rod in axial tension or compression，designated by N. 17

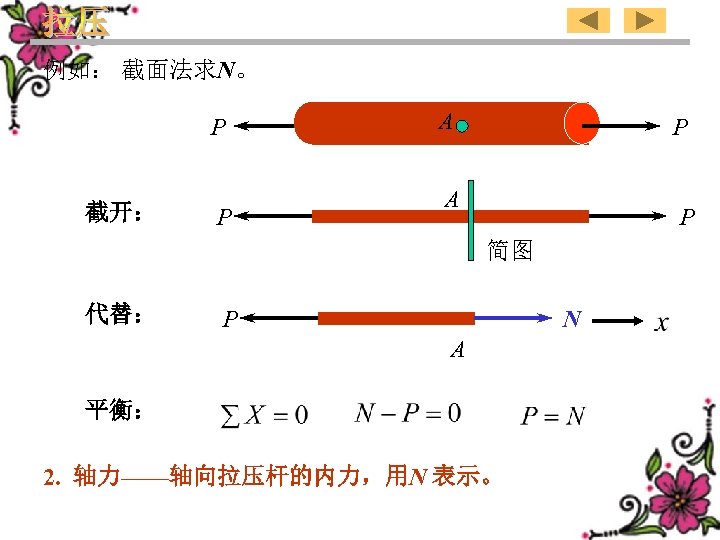例如： 截面法求N。 P 截开： P A P 简图 代替： P N A 平衡： 2. 轴力——轴向拉压杆的内力，用N 表示。

3). Sign conventions for the axial force: axial force N (tensile force)is positive when its direction point to the outward direction of the normal line of the section, (compressive force)negative inward N N N> 0 N <0 3、 Diagram of the axial force— sketch expression of N (x) meaning ①Reflected the variety relation between the corresponding axial force and the position of the section. N P + ②Find out value of the maximum axial x force and the position of the section in which the maximum axial force act. That is to determine the position of the critical section and supply the information for the calculation of strength. 19

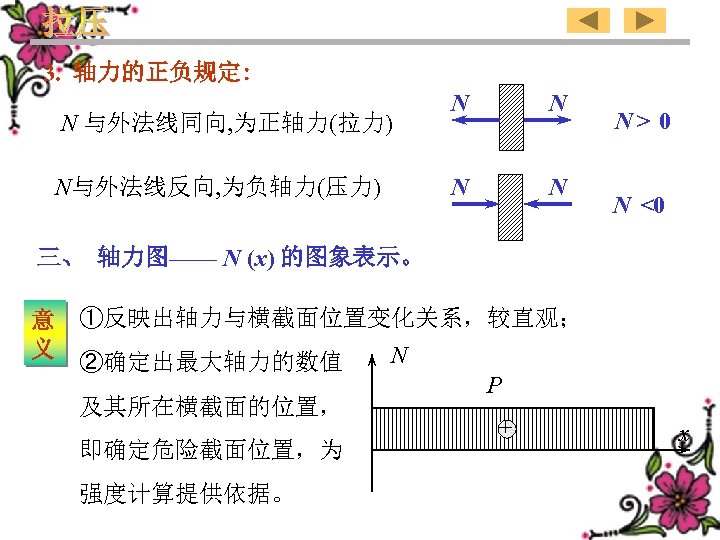3. 轴力的正负规定: N与外法线反向, 为负轴力(压力) N N N 与外法线同向, 为正轴力(拉力) N N N> 0 N <0 三、 轴力图—— N (x) 的图象表示。 意 义 ①反映出轴力与横截面位置变化关系，较直观； ②确定出最大轴力的数值 及其所在横截面的位置， 即确定危险截面位置，为 强度计算提供依据。 N P + x

Example 1 The forces with magnitudes 5 P、8 P、4 P and P act respectively at points A、B、C、D of the rod. Their directions are shown in the figure. Try to plot the diagram of the axial force of the rod. O A PA N 1 A B PB B C D PC PD C D PA PB PC PD Solution： Determine the internal force N 1 in segment OA. Take the free body as shown in the figure. 21

[例1] 图示杆的A、B、C、D点分别作用着大小为 5 P、8 P、4 P、 P 的力，方向如图，试画出杆的轴力图。 O A PA N 1 A PA B PB 解： 求OA段内力N 1：设置截面如图 C D PC PD

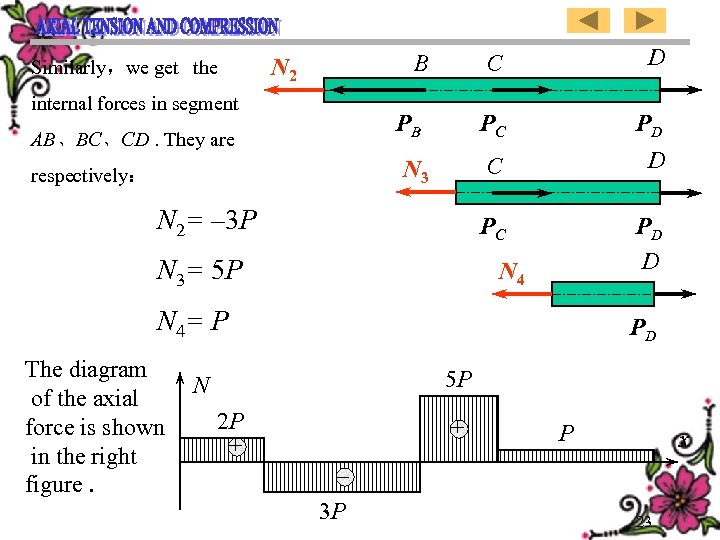Similarly，we get the C C PB AB、BC、CD. They are N 3 respectively： N 2= – 3 P N 3= 5 P PD D PC internal forces in segment D PC B N 2 PD D N 4= P The diagram of the axial force is shown in the right figure. PD 5 P N 2 P + + – 3 P P x 23

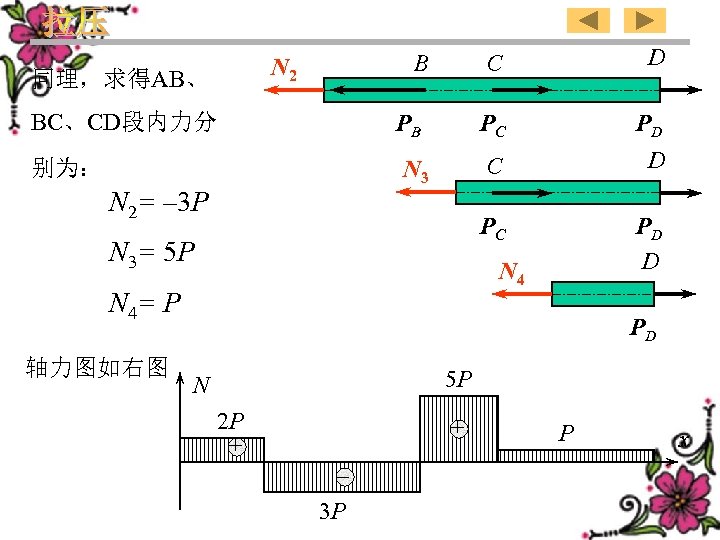BC、CD段内力分 PC 别为： N 3 N 2= – 3 P N 3= 5 P D PD D N 4= P 轴力图如右图 PD C PB D PC 同理，求得AB、 C B N 2 PD 5 P N 2 P + + – 3 P P x

Characteristic of the diagram of the axial force：Value of sudden change = concentrated load Simple method to plot the diagram of axial force： From the left to the right: If meeting the force P to the left ，the increase of the axial force N is positive； If meeting the force to the right ，the increase of the axial force N is negative. 8 k. N 5 k. N + 3 k. N 8 k. N – 3 k. N 25

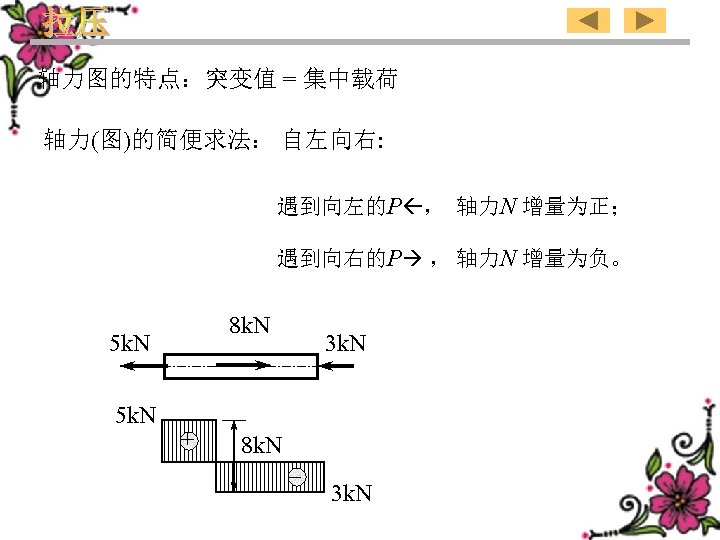轴力图的特点：突变值 = 集中载荷 轴力(图)的简便求法： 自左向右: 遇到向左的P ， 轴力N 增量为正； 遇到向右的P ， 轴力N 增量为负。 8 k. N 5 k. N + 3 k. N 8 k. N – 3 k. N

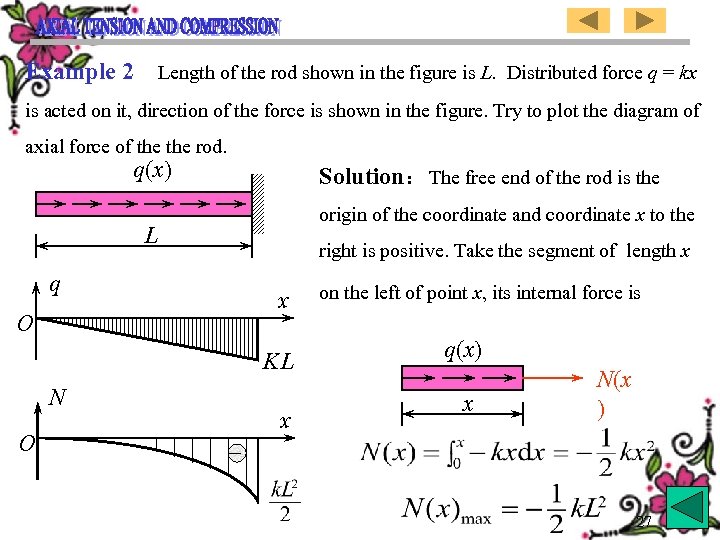Example 2 Length of the rod shown in the figure is L. Distributed force q = kx is acted on it, direction of the force is shown in the figure. Try to plot the diagram of axial force of the rod. q(x) Solution：The free end of the rod is the origin of the coordinate and coordinate x to the L right is positive. Take the segment of length x q x O KL N x – on the left of point x, its internal force is q(x) x N(x ) 27 O

[例2] 图示杆长为L，受分布力 q = kx 作用，方向如图，试画出 杆的轴力图。 解：x 坐标向右为正，坐标原点在 q(x) 自由端。 取左侧x 段为对象，内力N(x)为： L q x O q. L N x – q(x) x N(x ) O

§ 1– 3 STRESSES ON THE SECTION AND STRENGTH CONDITIONS Bring forward the problem： P P 1). The magnitude of the internal force can not scale the strength of the structure member. 2). Strength：①Intensity of the distributed internal forces in the section stress； ②The load-bearing capacity of the material. 1、Concept of stress 1). Definition：Intensity of the internal force due to the external forces. 29

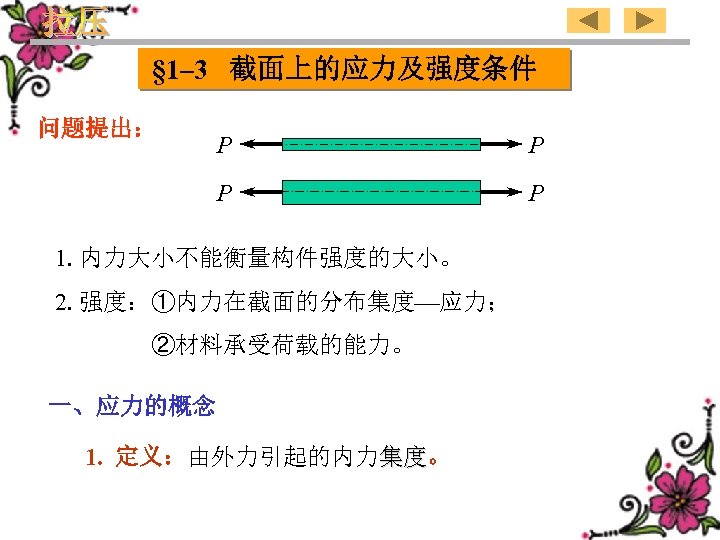§ 1– 3 截面上的应力及强度条件 问题提出： P P 1. 内力大小不能衡量构件强度的大小。 2. 强度：①内力在截面的分布集度 应力； ②材料承受荷载的能力。 一、应力的概念 1. 定义：由外力引起的内力集度。 集度

Under most cases distribution of the internal force inside engineering members is not uniform. Definition of intensity is neither accurate and important because breakage or failure often begins from the point at which intensity of the internal force is maximum. 2). Expression of stress： ①Average stress： P M A ②Whole stress（sum stress）： 31

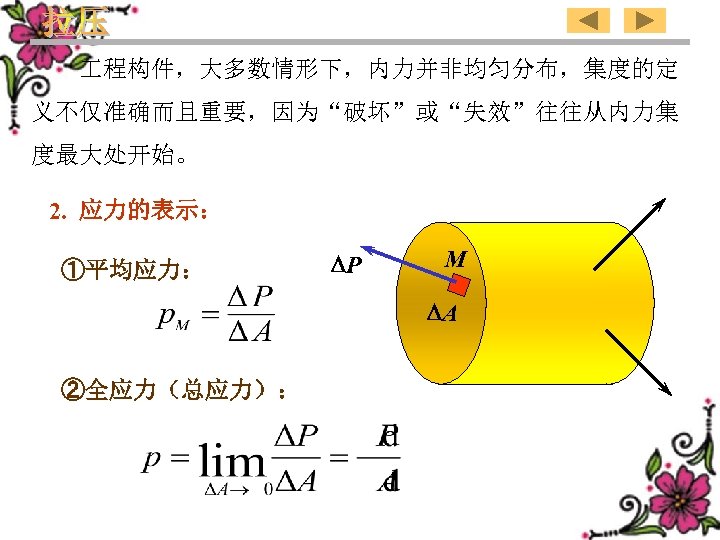程构件，大多数情形下，内力并非均匀分布，集度的定 义不仅准确而且重要，因为“破坏”或“失效”往往从内力集 度最大处开始。 2. 应力的表示： ①平均应力： P M A ②全应力（总应力）：

③Whole stress may be decomposed into: a. Stress perpendicular to the section is called“normal stress” p M b. Stress lying in the section is called“shearing stress” 33

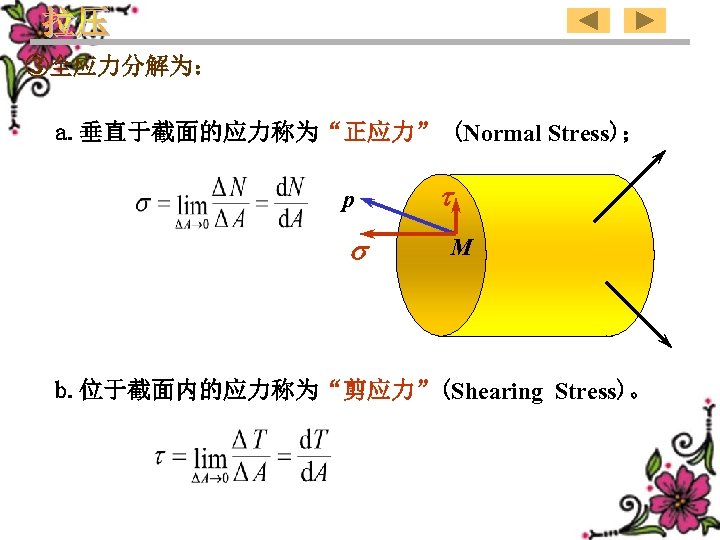③全应力分解为： a. 垂直于截面的应力称为“正应力” (Normal Stress)； p M b. 位于截面内的应力称为“剪应力”(Shearing Stress)。

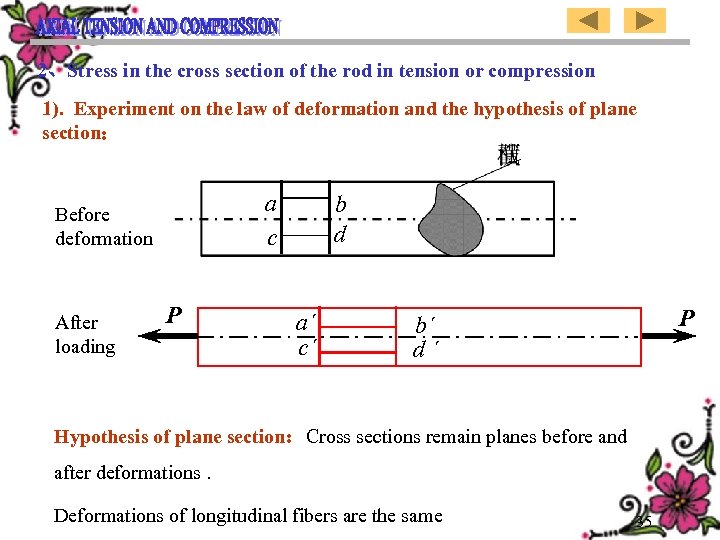2、Stress in the cross section of the rod in tension or compression 1). Experiment on the law of deformation and the hypothesis of plane section： a c Before deformation After loading P b d a´ c´ P b´ d´ Hypothesis of plane section：Cross sections remain planes before and after deformations. Deformations of longitudinal fibers are the same 35

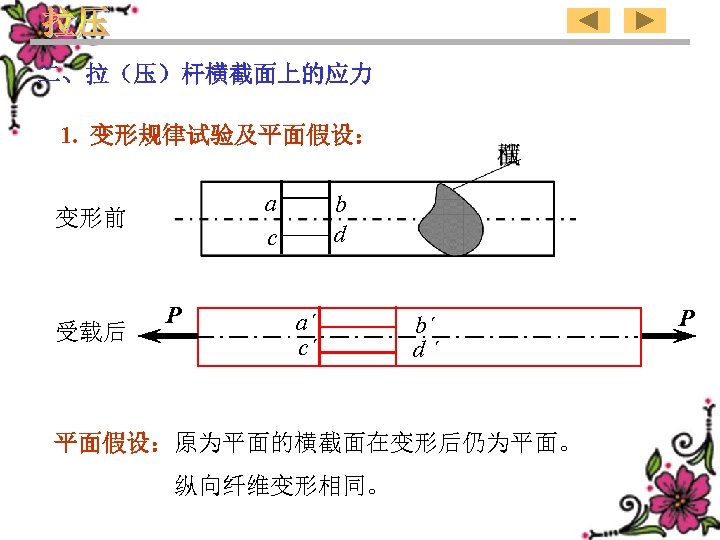二、拉（压）杆横截面上的应力 1. 变形规律试验及平面假设： a c 变形前 受载后 P b d a´ c´ b´ d´ 平面假设：原为平面的横截面在变形后仍为平面。 纵向纤维变形相同。 P

The material is homogeneous and , its deformation is uniform , so the internal force is distributed uniformly。 2. Tensile stress： P N(x) Normal stress due to the axial forces — ： distributes uniformly in the cross section. 3. Critical section and the maximum working stress ： Critical section：The section in which internal force is maximum and of which the dimension is smallest. Critical point：The point at which the stress is maximum. 37

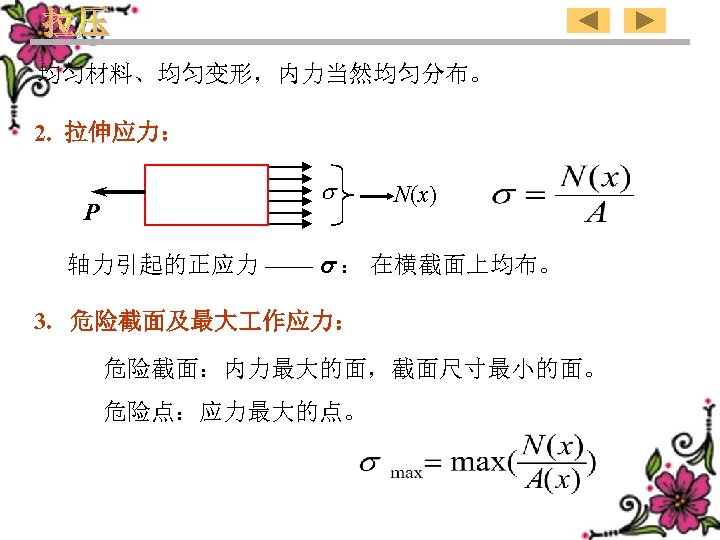均匀材料、均匀变形，内力当然均匀分布。 2. 拉伸应力： P N(x) 轴力引起的正应力 —— ： 在横截面上均布。 3. 危险截面及最大 作应力： 危险截面：内力最大的面，截面尺寸最小的面。 危险点：应力最大的点。

4). Application conditions of the formula： Straight rod、cross section of the rod is without sudden change、there is a certain distance from the section to the point at which the load acts. 5). Saint-Venant principle： Distribution and magnitude of the stress in the section at a certain distance from the point at which the load is acted are not affected by the acting form of external loads. 6). Stress concentration： Stress increases abruptly near the cross section with a sudden change in dimension　 39

4. 公式的应用条件： 直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 5. Saint-Venant原理： 离开载荷作用处一定距离，应力分布与大小不受外载荷作 用方式的影响。 6. 应力集中（Stress Concentration）： 在截面尺寸突变处，应力急剧变大。　

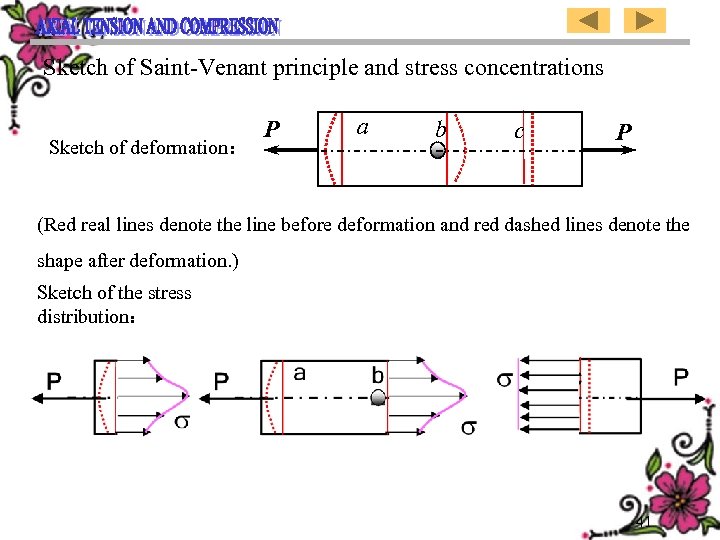Sketch of Saint-Venant principle and stress concentrations Sketch of deformation： P a b c P (Red real lines denote the line before deformation and red dashed lines denote the shape after deformation. ) Sketch of the stress distribution： 41

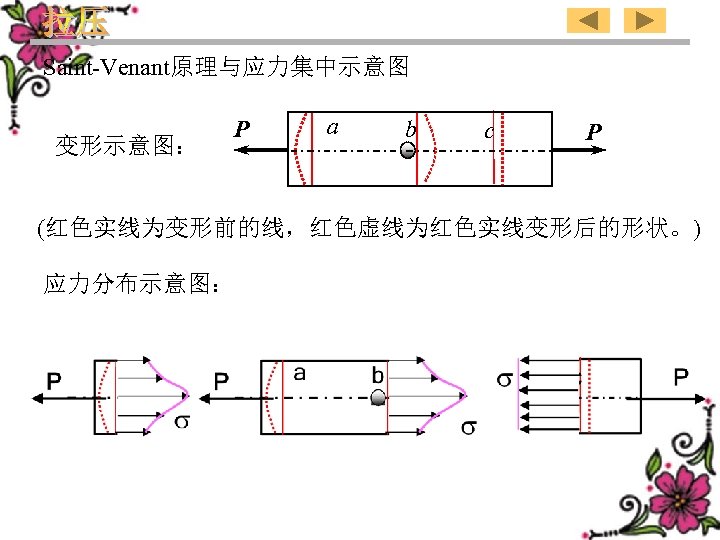Saint-Venant原理与应力集中示意图 变形示意图： P a b c P (红色实线为变形前的线，红色虚线为红色实线变形后的形状。) 应力分布示意图：

7). Criterion of the strength design：　　　　　 That structure members are ensured not to be wrecked and have certain safe degree. where：[ ]—allowable stress， max– the maximum working stress at the critical point. Three kinds of calculation of strength may be done according to the criterion of strength: ①Check the strength： ②Design the dimension of the section： ③Determine the allowable load： 43

7. 强度设计准则（Strength Design）：　　　　　 保证构件不发生强度破坏并有一定安全余量的条件准则。 其中：[ ]--许用应力， max--危险点的最大 作应力。 依强度准则可进行三种强度计算： ①校核强度： ②设计截面尺寸： ③许可载荷：

Example 3 A circular rod is subjected to a tensile force P =25 k. N. Its diameter is d =14 mm and its allowable stress is [ ]=170 MPa. Try to check the strength of the rod. Solution：① Axial force：N = P =25 k. N ②Stress： ③Check the strength： ④Conclusion：The strength of the rod satisfies request. The rod can work normally. 45

[例3] 已知一圆杆受拉力P =25 k N，直径 d =14 mm，许用应力 [ ]=170 MPa，试校核此杆是否满足强度要求。 解：① 轴力：N = P =25 k. N ②应力： ③强度校核： ④结论：此杆满足强度要求，能够正常 作。

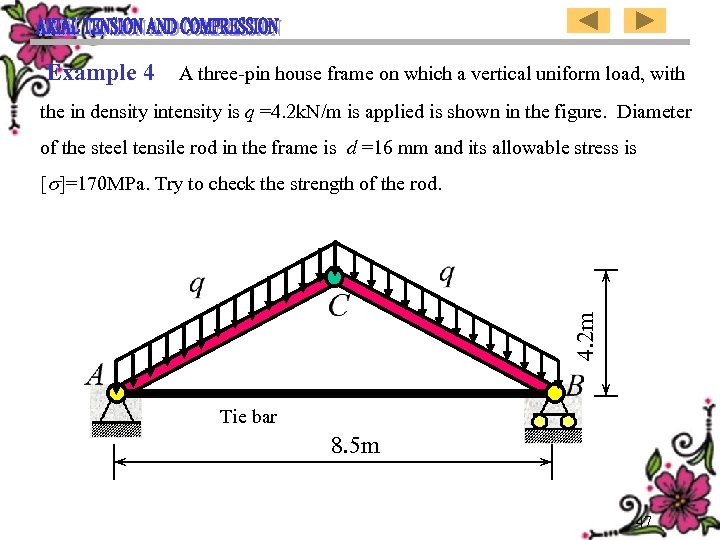Example 4 A three-pin house frame on which a vertical uniform load, with the in density intensity is q =4. 2 k. N/m is applied is shown in the figure. Diameter of the steel tensile rod in the frame is d =16 mm and its allowable stress is 4. 2 m [ ]=170 MPa. Try to check the strength of the rod. Tie bar 8. 5 m 47

[例4] 已知三铰屋架如图，承受竖向均布载荷，载荷的分布 集度为：q =4. 2 k. N/m，屋架中的钢拉杆直径 d =16 mm，许用 试校核钢拉杆的强度。 4. 2 m 应力[ ]=170 M Pa。 钢拉杆 8. 5 m

4. 2 m Solution： ① Determine the reactions first according to the global equilibrium HA RA Tie bar 8. 5 m RB 49

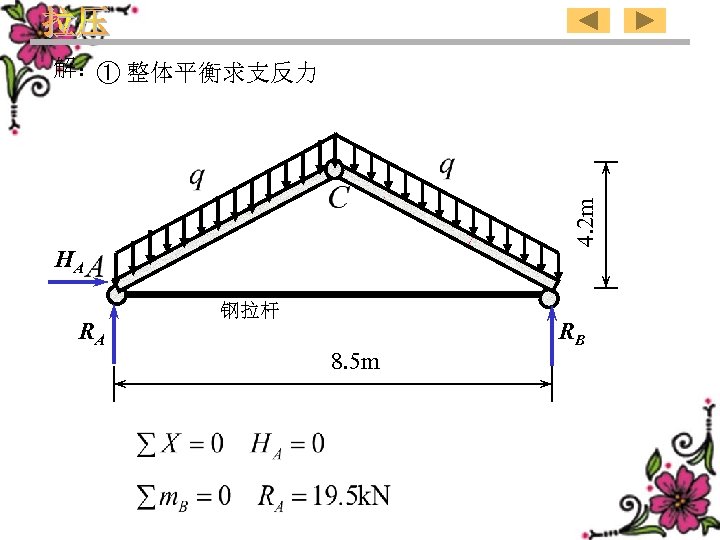4. 2 m 解： 整体平衡求支反力 ① HA RA 钢拉杆 8. 5 m RB

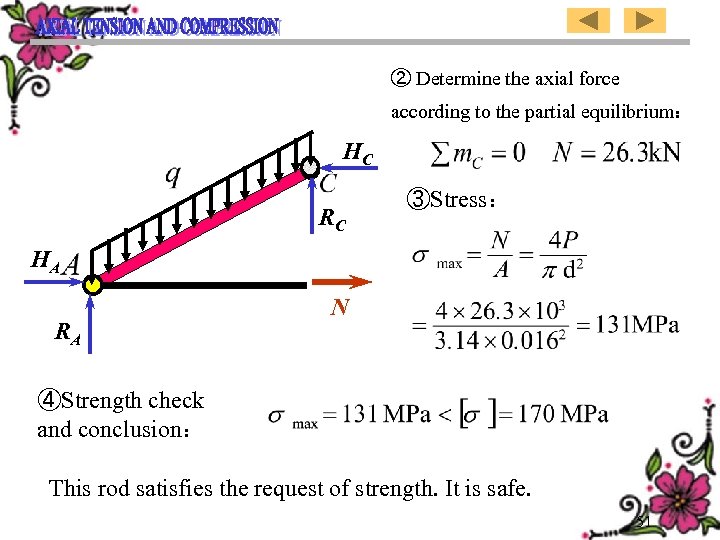② Determine the axial force according to the partial equilibrium： HC RC ③Stress： HA RA N ④Strength check and conclusion： This rod satisfies the request of strength. It is safe. 51

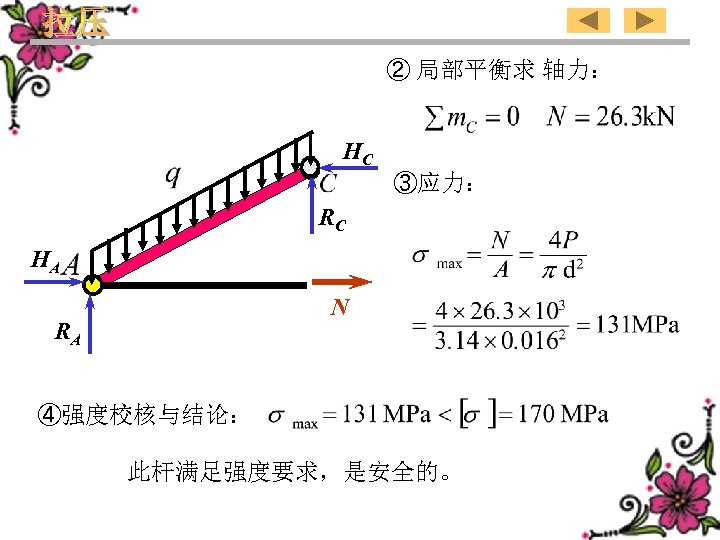② 局部平衡求 轴力： HC ③应力： RC HA N RA ④强度校核与结论：　　 此杆满足强度要求，是安全的。

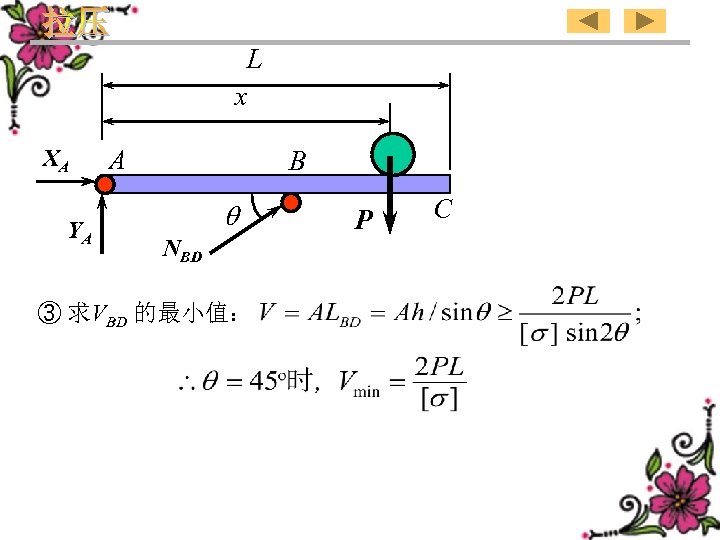
Example 5 A simple crane is shown in the figure. AC is a rigid beam ，sum weight of the hoist and heavy body that is lifted is P. What should be the angle so that the rod BD has the minimum weight？ The allowable stress of the rod [ ] is known. L x A Analysis： B P C h D 53

[例5] 简易起重机构如图，AC为刚性梁，吊车与吊起重物总重 为P，为使 BD杆最轻，角 应为何值？ 已知 BD 杆的许用应力 为[ ]。 L x A B h D 分析： P C

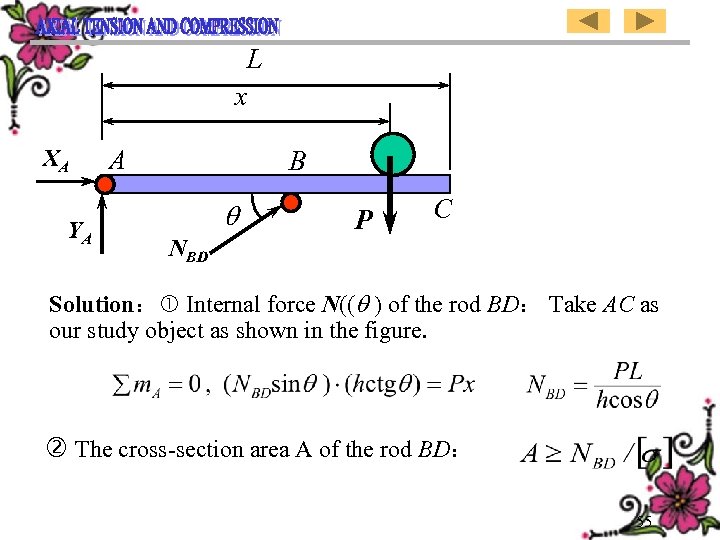L x XA YA A B NBD P C Solution： Internal force N(( ) of the rod BD： Take AC as our study object as shown in the figure. The cross-section area A of the rod BD： 55

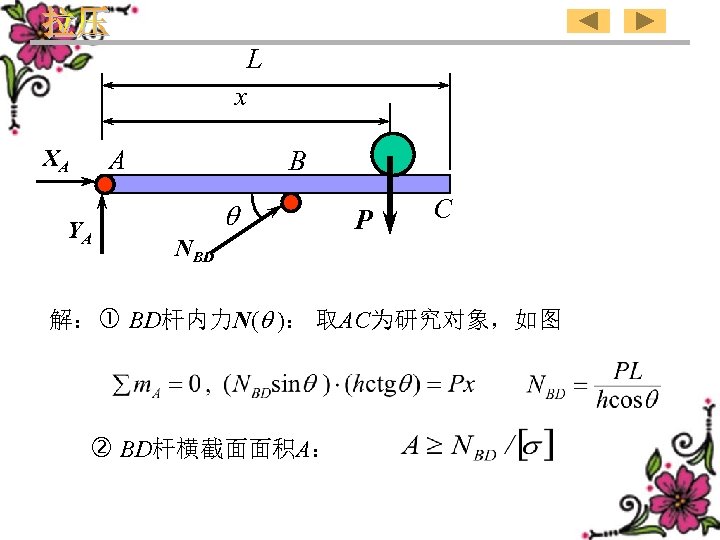L x A XA YA B NBD P C 解： BD杆内力N( )： 取AC为研究对象，如图 BD杆横截面面积A：

L x XA YA A B NBD P C ③ Determine the minimum value of VBD ： 67

L x XA YA A B NBD ③ 求VBD 的最小值： P C

3、Stresses in the inclined section of the rod in tension or compression k Assume a straight rod is subjected to a tensile force P. Determine the stress in the inclined section k-k. Solution: Adopt the method of section. According to the equilibrium equation：P =P then P P k k Pa P k A : Area of the inclined section；P ：Internal force in the inclined section. From geometric relation Substituting： into the above it formula we get Whole stress in the inclined section： 59

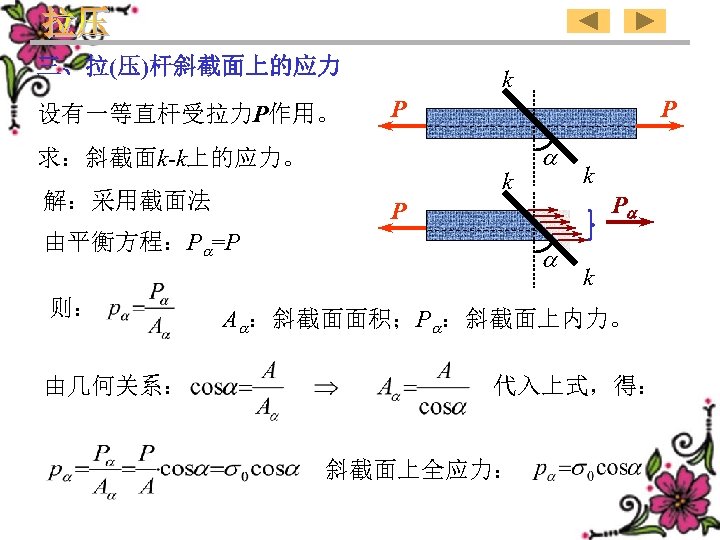三、拉(压)杆斜截面上的应力 设有一等直杆受拉力P作用。 k P 求：斜截面k-k上的应力。 解：采用截面法 P k 由几何关系： k Pa P 由平衡方程：P =P 则： k A ：斜截面面积；P ：斜截面上内力。 代入上式，得： 斜截面上全应力：

Whole stress in the inclined section： k P P Decomposition： p = k k a P a It indicates the change of stresses in different sections k through a point. As = 0°， As =90°， a (The maximum normal stress exists in the cross section) As = ± 45°， (The maximum shearing stress exists As = 0, 90°， in the inclined section of 45 °) 61 pa

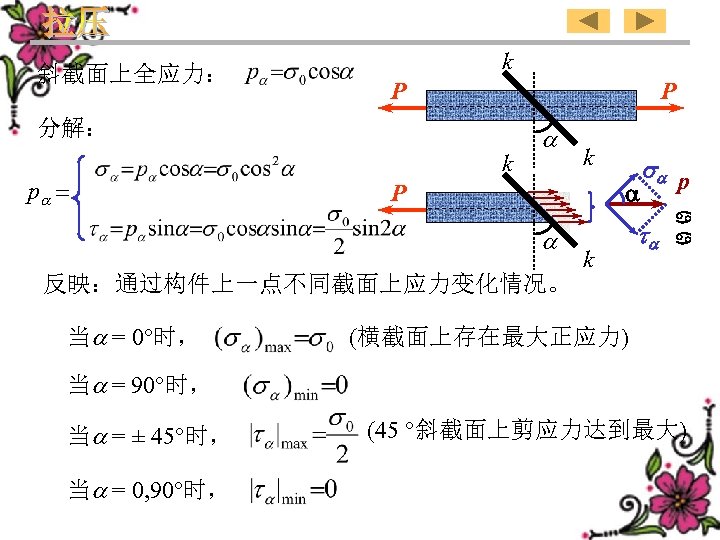斜截面上全应力： k P P 分解： p = k P 反映：通过构件上一点不同截面上应力变化情况。 当 = 0°时， k a p a k a a a (横截面上存在最大正应力) 当 = 90°时， 当 = ± 45°时， 当 = 0, 90°时， (45 °斜截面上剪应力达到最大)

Complementary：　　　　　 1. State of stress at a point：There are countless sections through a point. Sum of stresses in the different section through a point is called the state of stress at this point. 2、Element： Element— delegate of a point inside the member, infinitesimal geometric body which envelops the study point. The element in common use is just hexahedron properties of an element—a、stress is distributed uniformly in an arbitrary parallel arbitrary plane；b、stresses in the parallel plane opposite plane P M are equal. 3、stress element at a point M in the rod in tension or compression: 　　　　 　　 63

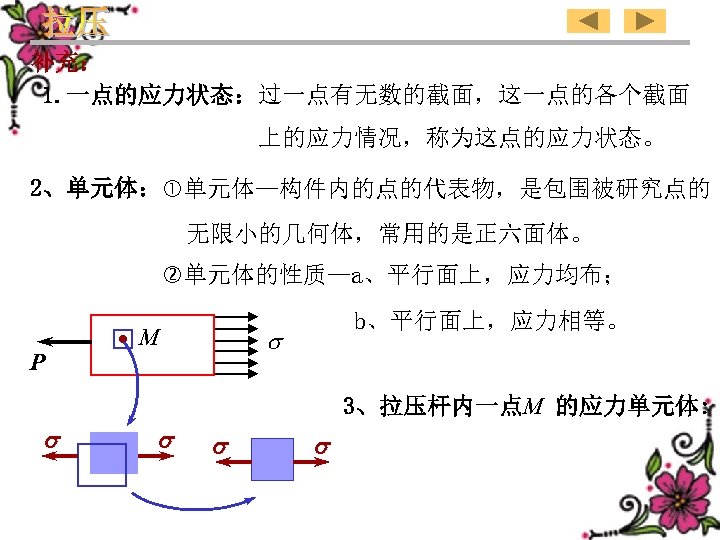补充：　　　　　 1. 一点的应力状态：过一点有无数的截面，这一点的各个截面 上的应力情况，称为这点的应力状态。 2、单元体： 单元体—构件内的点的代表物，是包围被研究点的 无限小的几何体，常用的是正六面体。 单元体的性质—a、平行面上，应力均布； P M b、平行面上，应力相等。 3、拉压杆内一点M 的应力单元体: 　　　　　

4、Stress in the inclined section of the rod in tension or compression Take a free body as shown in the Fig. 3. is positive if it is along countclockwise； t is positive if it makes the free body rotate clockwise. From the equilibrium of the free body we get： x Fig. 3 65

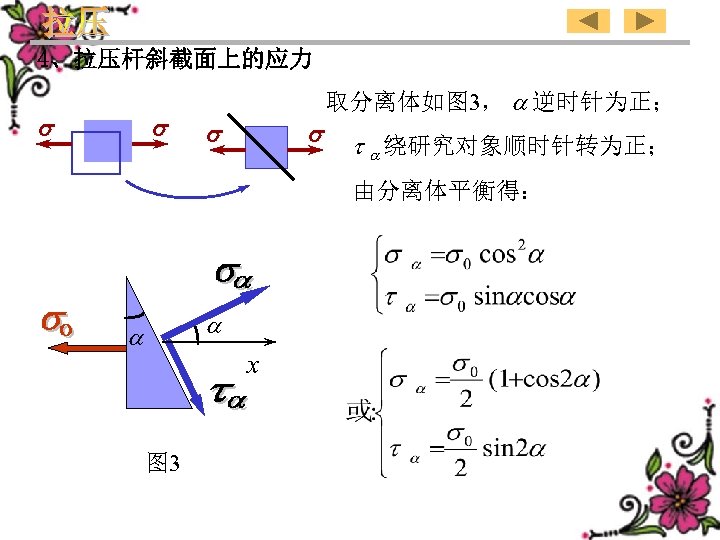4、拉压杆斜截面上的应力 取分离体如图 3， 逆时针为正； t 绕研究对象顺时针转为正； 由分离体平衡得： x 图 3

Example 6 A rod, which the diameter d =1 cm is subjected to a tensile force P =10 k. N. Determine the maximum shearing stress , the normal stress and shearing stress in the inclined section of an angle 30°about the cross section. Solution：Stresses in the inclined section of the rod in tension or compression can be determined directly by the formula： 67

[例6] 直径为d =1 cm 杆受拉力P =10 k. N的作用，试求最大剪应 力，并求与横截面夹角 30°的斜截面上的正应力和剪应力。 解：拉压杆斜截面上的应力，直接由公式求之：

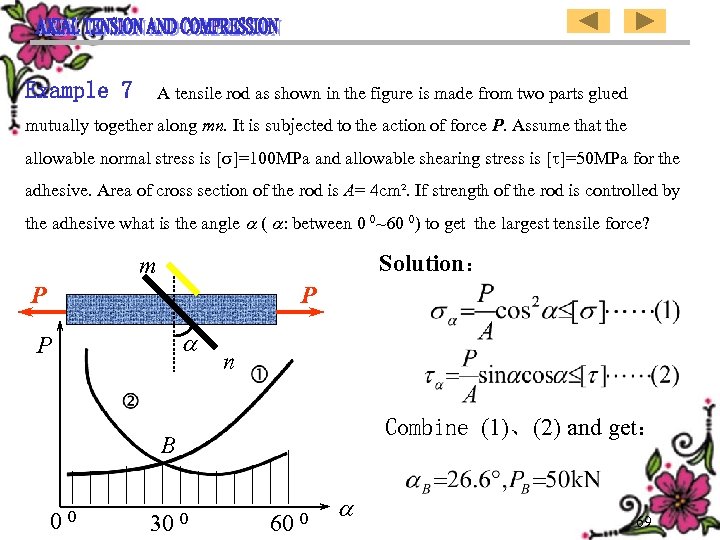Example 7 A tensile rod as shown in the figure is made from two parts glued mutually together along mn. It is subjected to the action of force P. Assume that the allowable normal stress is [ ]=100 MPa and allowable shearing stress is [ ]=50 MPa for the adhesive. Area of cross section of the rod is A= 4 cm². If strength of the rod is controlled by the adhesive what is the angle ( : between 0 0~60 0) to get the largest tensile force? Solution： m P P P n Combine (1)、(2) and get： B 0 0 30 0 69

[例7]图示拉杆沿mn由两部分胶合而成, 受力P，设胶合面的许用 拉应力为[ ]=100 MPa ；许用剪应力为[ ]=50 MPa ，并设杆的 强度由胶合面控制, 杆的横截面积为A= 4 cm²，试问: 为使杆承受 最大拉力, 角值应为多大? (规定: 在 0~60度之间)。 m P 解： P P n 联立(1)、(2)得： B 0 0 30 0 60 0

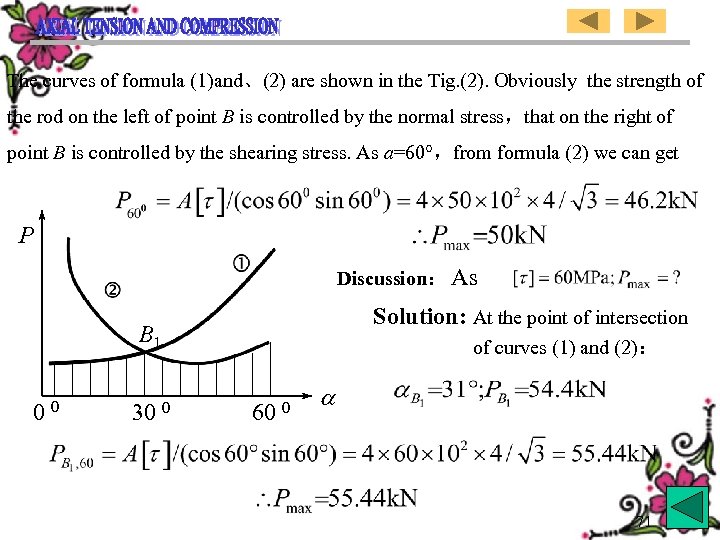The curves of formula (1)and、(2) are shown in the Tig. (2). Obviously the strength of the rod on the left of point B is controlled by the normal stress，that on the right of point B is controlled by the shearing stress. As a=60°，from formula (2) we can get P Discussion：As Solution: At the point of intersection of curves (1) and (2)： B 1 00 30 0 60 0 71

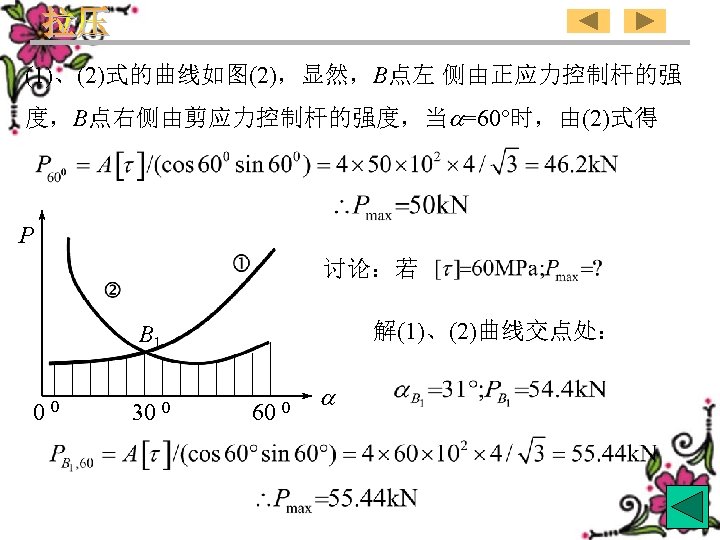(1)、(2)式的曲线如图(2)，显然，B点左 侧由正应力控制杆的强 度，B点右侧由剪应力控制杆的强度，当 =60°时，由(2)式得 P 讨论：若 解(1)、(2)曲线交点处： B 1 00 30 0 60 0

§ 1－4 DEFORMATION OF THE ROD IN AXIAL TENSION AND COMPRESSION LAW OF ELASTICITY 1、Deformation and strain of the rod in tension or compression　　　　　　　 　　 Cross section a c 1)、The whole longitudinal deformation of the rod： b d L 2)、Strain：linear deformation per unit length. 3)、Average stain： 73

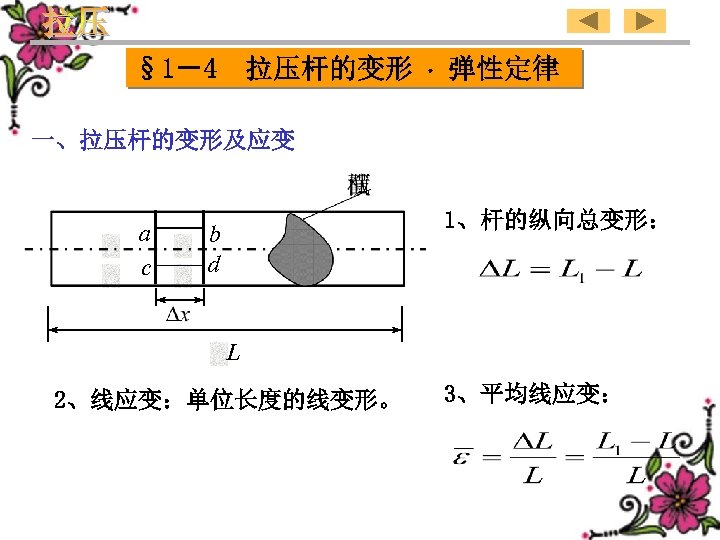§ 1－4 拉压杆的变形 弹性定律 一、拉压杆的变形及应变　　　　　 a c 1、杆的纵向总变形： b d L 2、线应变：单位长度的线变形。 3、平均线应变：

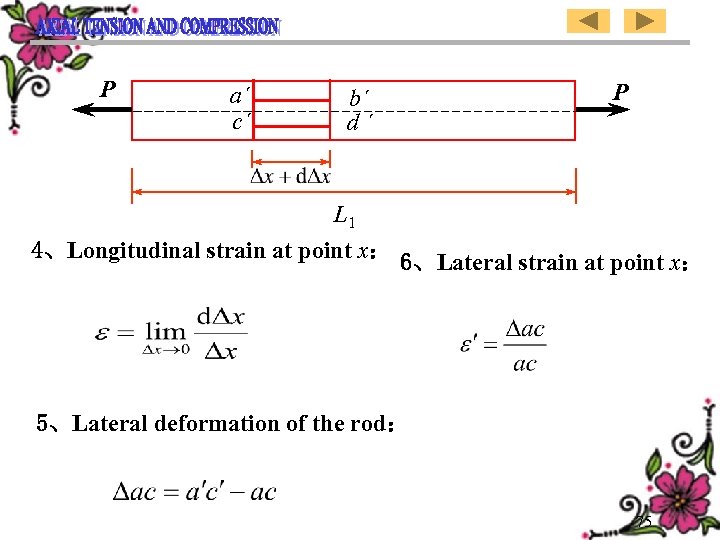P a´ c´ b´ d´ P L 1 4、Longitudinal strain at point x： 6、Lateral strain at point x： 5、Lateral deformation of the rod： 75

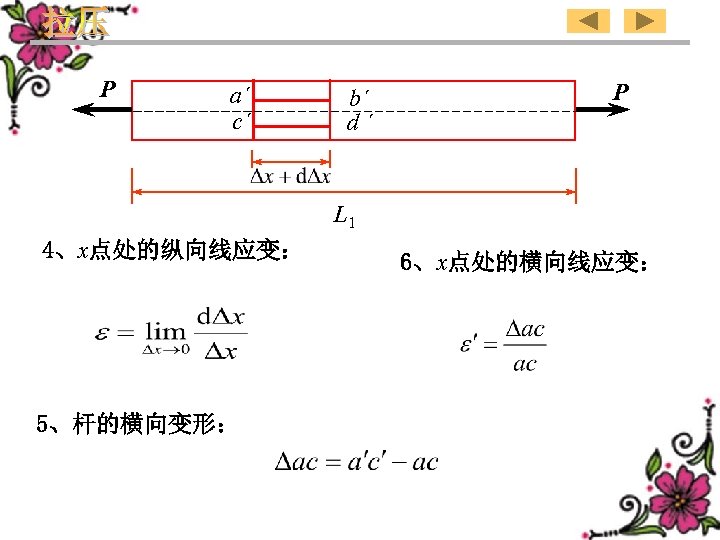P a´ c´ b´ d´ P L 1 4、x点处的纵向线应变： 5、杆的横向变形： 6、x点处的横向线应变：

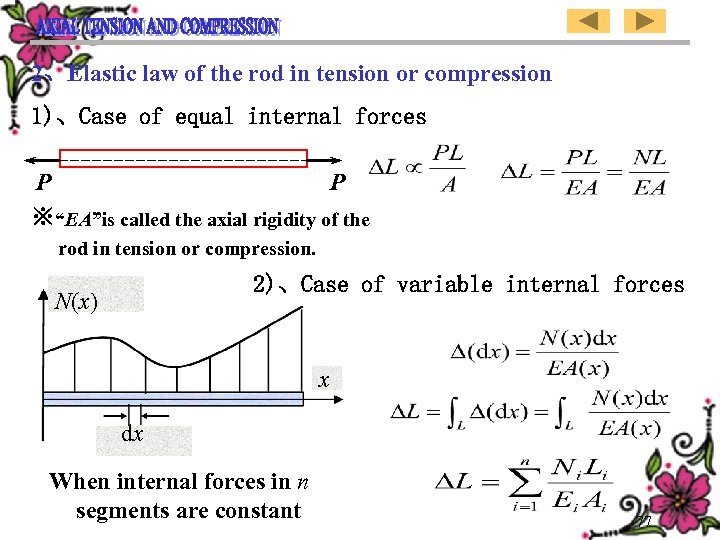2、Elastic law of the rod in tension or compression　　　　　　　 1)、Case of equal internal forces　　　　　 P P ※“EA”is called the axial rigidity of the rod in tension or compression. 　　　　　 2)、Case of variable internal forces 　　　　　 N(x) x dx When internal forces in n segments are constant　　 77

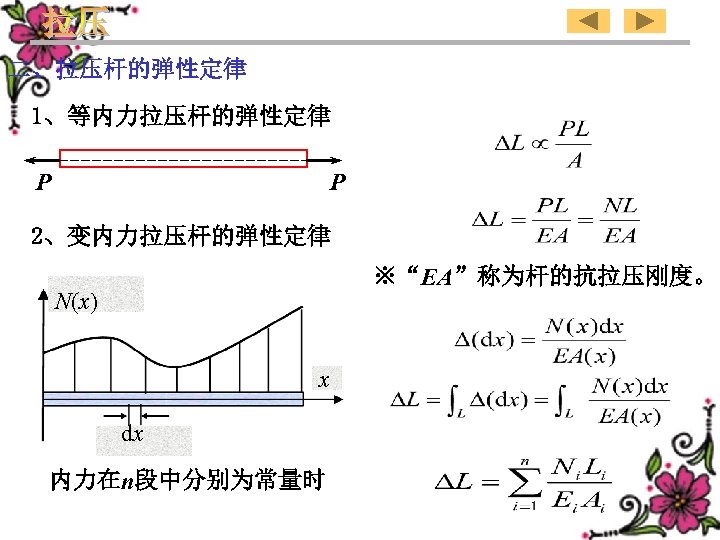二、拉压杆的弹性定律　　　　　 1、等内力拉压杆的弹性定律　　　　　 P P 2、变内力拉压杆的弹性定律　　　　　 ※“EA”称为杆的抗拉压刚度。　 N(x) x dx 内力在n段中分别为常量时　　　　　

3)、Elastic law in uniaxial stressed state　　　　 That is 4)、Possion , s ratio（or coefficient of the lateral deformation）　　　　　 or 3、Who firstly proposed the Elastic Law The Elastic Law is the important foundation of solid mechanics such Mechanics of Materials. Generally it is considered to be proposed firstly by the English scientist Hook (1635 -1703), So the Elastic Law is also called Hook, s Law. Actually , there was an early record of the proportional ration between force and deformation , which is 1500 years earlier than Hook. 79

3、单向应力状态下的弹性定律　　　　　 4、泊松比（或横向变形系数）　　　　　 三、是谁首先提出弹性定律是材料力学等固体力学一个非常重要的基础。一般 认为它是由英国科学家胡克(1635一1703)首先提出来的，所以通 常叫做胡克定律。其实，在胡克之前1500年，我国早就有了关于 力和变形成正比关系的记载。

东汉经学家郑玄(127— 200)对《考 记·弓人》中“量其力， 有三均”作了 这样的注释：“假令弓力胜三石，引之中三尺，弛 其弦，以绳缓擐之，每加物一石，则张一尺。” (图) “ 胡：请问， 弛其弦，以绳缓缓之” 是什么意思 ? 郑：这是讲测量弓力时，先将弓的弦 松开，另外用绳子松松地套住弓 的两端，然后加重物，测量。 胡：我明白了。这样弓体就没有初始应力，处于自然状态。

东汉经学家郑玄(127— 200)对《考 记·弓人》中“量其力， 有三均”作了 这样的注释：“假令弓力胜三石，引之中三尺，弛 其弦，以绳缓擐之，每加物一石，则张一尺。” (图) “ 胡：请问， 弛其弦，以绳缓缓之” 是什么意思 ? 郑：这是讲测量弓力时，先将弓的弦 松开，另外用绳子松松地套住弓 的两端，然后加重物，测量。 胡：我明白了。这样弓体就没有初始应力，处于自然状态。

郑：后来，到了唐代初期，贾公彦对我的注释又作了注疏，他说： 郑又云假令弓力胜三石，引之 中三尺者，此即三石力弓也。 必知弓力三石者，当弛其弦以绳缓擐之者，谓不张之，别以 一条 绳系两箭，乃加物一石张一尺、二石张二尺、三石张三 其中 “ 两萧” 就是指弓的两端。 尺。 胡：郑老先生讲“每加物一石，则张一尺”。和我讲的完全是同一 个意思。您比我早 1500 中就记录下这种正比关系，的确了不起， 真是令人佩服之至』我在 1686 年《关于中国文字和语言的研究 “ 和推测》一文中早就推崇过贵国的古代文化： 目前我们还只 是刚刚走到这个知识领域的边缘，然而一旦对它有了充分的认 识，就将会在我们面 前展现出一个迄今为止只被人们神话般 地加以描述的知识王国”。 83

郑：后来，到了唐代初期，贾公彦对我的注释又作了注疏，他说： 郑又云假令弓力胜三石，引之 中三尺者，此即三石力弓也。 必知弓力三石者，当弛其弦以绳缓擐之者，谓不张之，别以 一条 绳系两箭，乃加物一石张一尺、二石张二尺、三石张三 其中 “ 两萧” 就是指弓的两端。 尺。 胡：郑老先生讲“每加物一石，则张一尺”。和我讲的完全是同一 个意思。您比我早 1500 中就记录下这种正比关系，的确了不起， 真是令人佩服之至』我在 1686 年《关于中国文字和语言的研究 “ 和推测》一文中早就推崇过贵国的古代文化： 目前我们还只 是刚刚走到这个知识领域的边缘，然而一旦对它有了充分的认 识，就将会在我们面 前展现出一个迄今为止只被人们神话般 地加以描述的知识王国”。

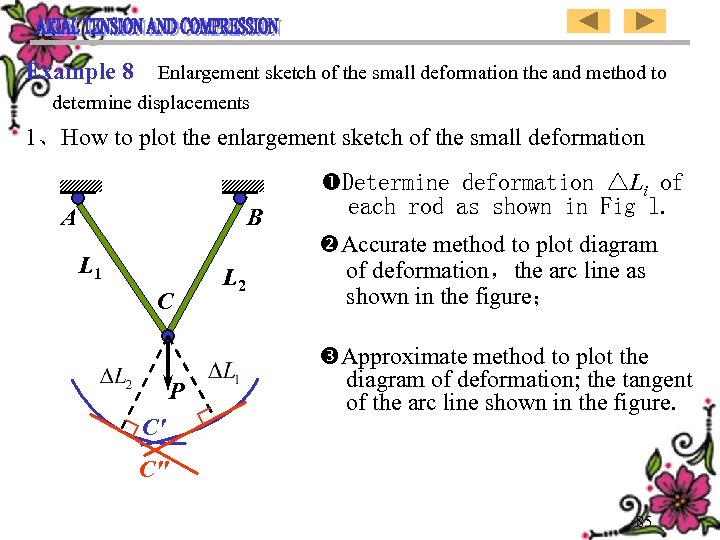
Example 8 Enlargement sketch of the small deformation the and method to determine displacements 1、How to plot the enlargement sketch of the small deformation A B L 1 C P C' L 2 Determine deformation △Li of each rod as shown in Fig l. Accurate method to plot diagram of deformation，the arc line as shown in the figure； Approximate method to plot the diagram of deformation; the tangent of the arc line shown in the figure. C" 85

[例8] 小变形放大图与位移的求法。 1、怎样画小变形放大图？ 求各杆的变形量△Li ，如图 1； A B 变形图严格画法，图中弧线； L 1 C P C' C" L 2 变形图近似画法，图中弧之切线。

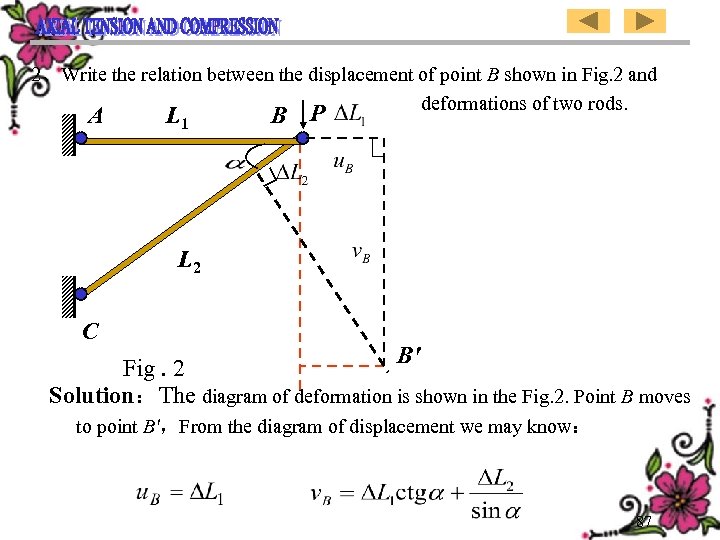2、Write the relation between the displacement of point B shown in Fig. 2 and deformations of two rods. A L 1 B P L 2 C B' Fig. 2 Solution：The diagram of deformation is shown in the Fig. 2. Point B moves to point B'，From the diagram of displacement we may know： 87

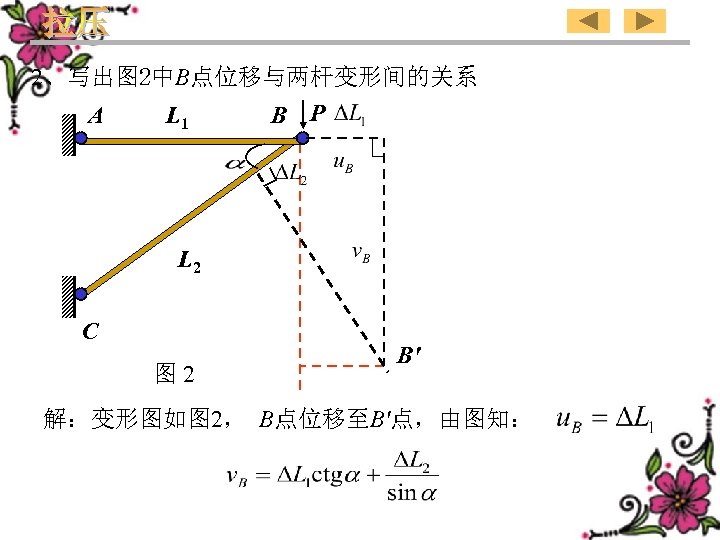2、写出图 2中B点位移与两杆变形间的关系 A L 1 B P L 2 C 图 2 B' 解：变形图如图 2， B点位移至B'点，由图知：

Example 9 Suppose the crossbeam ABCD is rigid. A steel cable with the cross -section area 76. 36 mm² is around a pulley without friction. Knowing P=20 k. N，E =177 GPa. Determine the stress of the steel cable and the upright displacement of point C. Solution：method 1：Enlargement sketch method of the small deformation. A YA 1)Determine the internal force of the steel cable: Take ABD as our study object： P 400 800 XA A 60° D C B B T C T D 2) Stress and elongation of the steel cable P 89

[例9] 设横梁ABCD为刚梁，横截面面积为 76. 36 mm² 的钢索绕 过无摩擦的定滑轮。设 P=20 k. N，试求钢索内的应力和 C点的 垂直位移。设钢索的 E =177 GPa。 解：方法 1：小变形放大图法 A B 60° D 1）求钢索内力：以ABCD为研究对象 C P 400 800 XA A YA B T C T P D 2) 钢索的应力和伸长分别为：

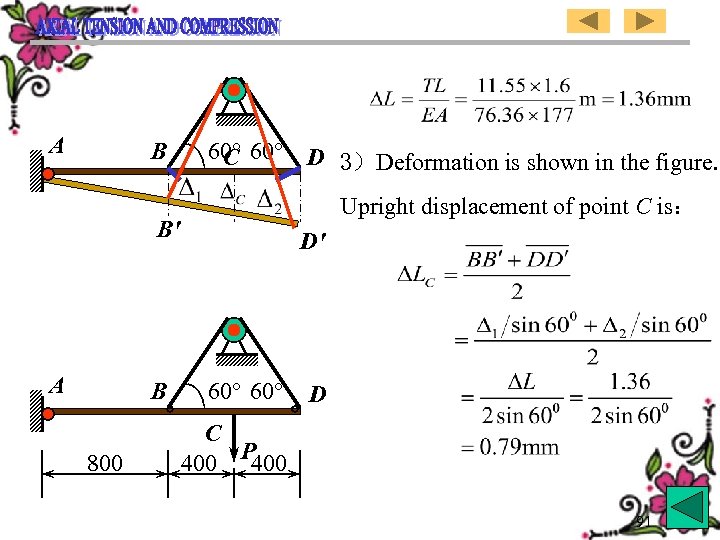A B 60° D 3）Deformation is shown in the figure. C Upright displacement of point C is： B' A B 800 D' 60° D C 400 P 400 91

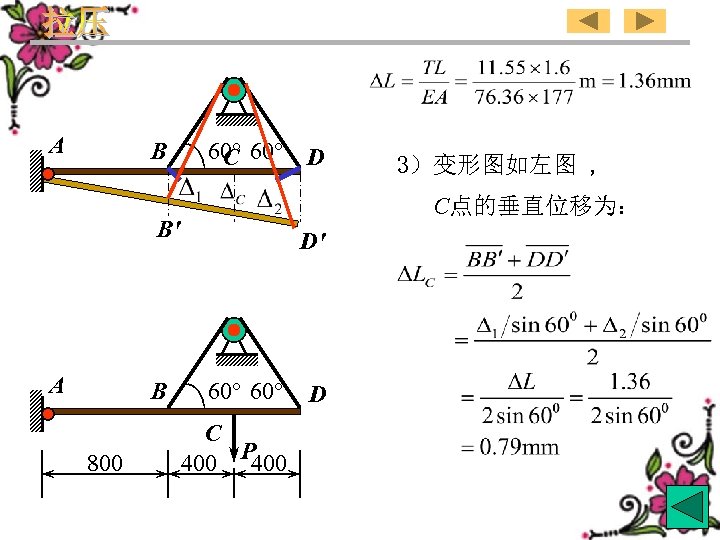A B 60° D C C点的垂直位移为： B' A B 800 3）变形图如左图 , D' 60° C 400 P 400 D

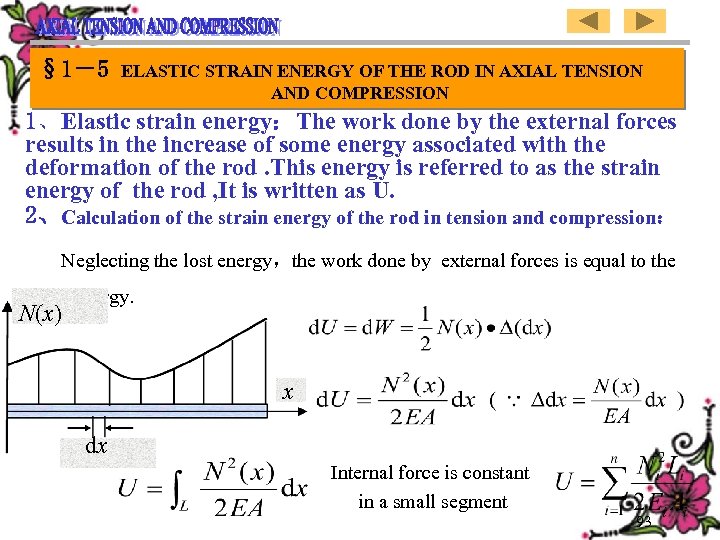§ 1－5 ELASTIC STRAIN ENERGY OF THE ROD IN AXIAL TENSION AND COMPRESSION 1、Elastic strain energy：The work done by the external forces results in the increase of some energy associated with the deformation of the rod. This energy is referred to as the strain energy of the rod , It is written as U. 2、Calculation of the strain energy of the rod in tension and compression： Neglecting the lost energy，the work done by external forces is equal to the strain energy. N(x) x dx Internal force is constant in a small segment 　　 　　　　 93

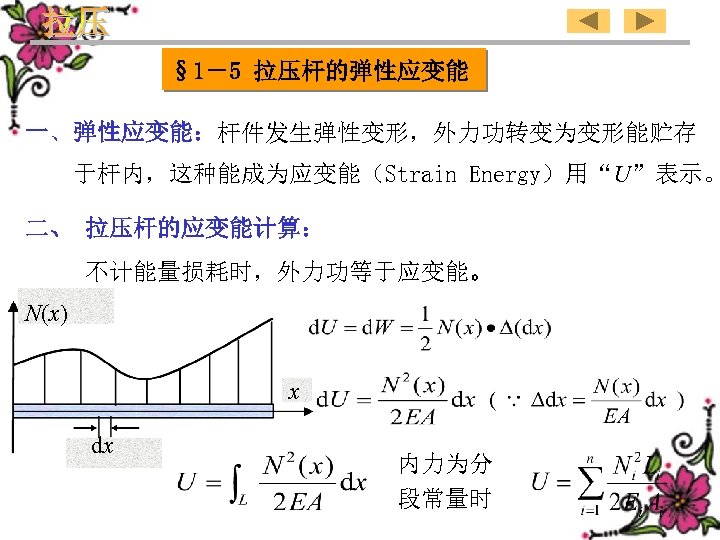§ 1－5 拉压杆的弹性应变能 一、弹性应变能：杆件发生弹性变形，外力功转变为变形能贮存 于杆内，这种能成为应变能（Strain Energy）用“U”表示。 二、 拉压杆的应变能计算： 不计能量损耗时，外力功等于应变能。 N(x) x dx 内力为分 段常量时　　 　　　　

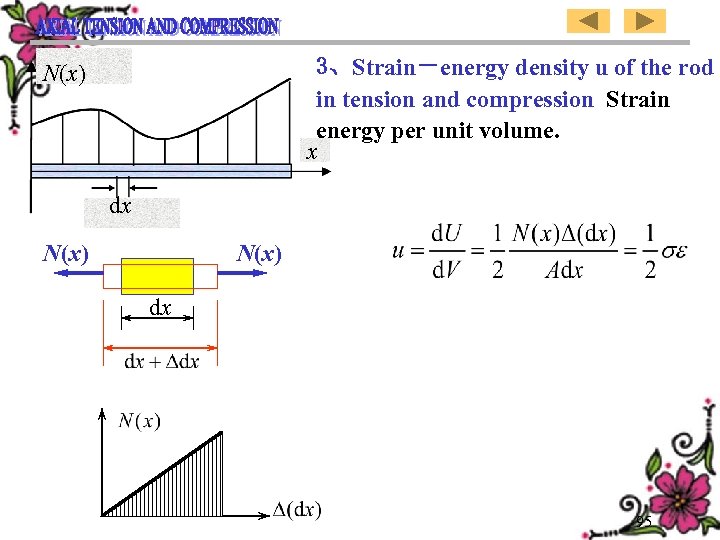3、Strain－energy density u of the rod in tension and compression Strain energy per unit volume. x N(x) dx 95

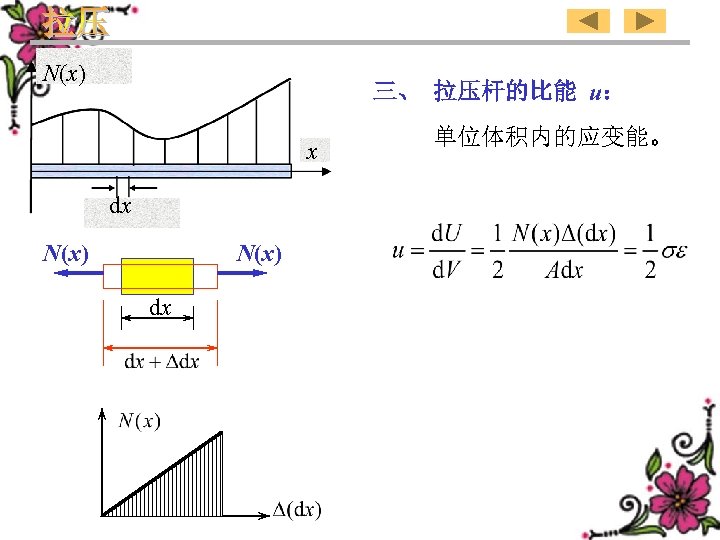N(x) 三、 拉压杆的比能 u： x dx N(x) dx 单位体积内的应变能。

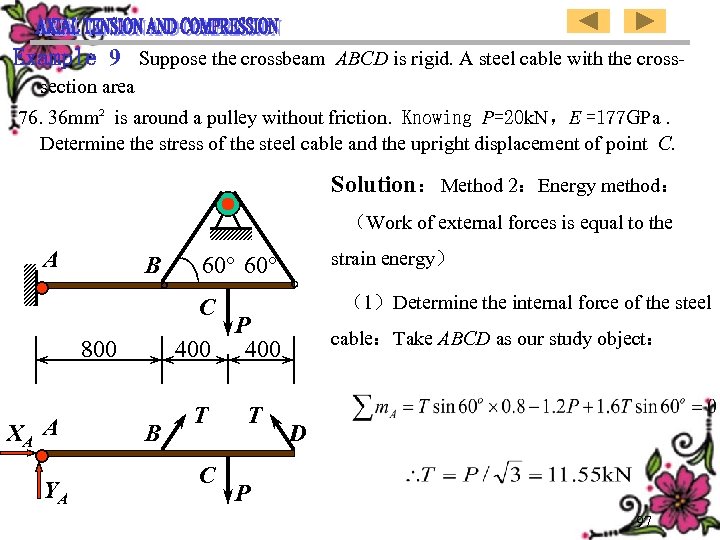Example 9 Suppose the crossbeam ABCD is rigid. A steel cable with the crosssection area 76. 36 mm² is around a pulley without friction. Knowing P=20 k. N，E =177 GPa. Determine the stress of the steel cable and the upright displacement of point C. Solution：Method 2：Energy method： （Work of external forces is equal to the A B strain energy） 60° （1）Determine the internal force of the steel C P 400 800 XA A YA B T C T cable：Take ABCD as our study object： D P 97

[例9] 设横梁ABCD为刚梁，横截面面积为 76. 36 mm² 的钢索绕 过无摩擦的定滑轮。设 P=20 k. N，试求钢索内的应力和 C点的 垂直位移。设钢索的 E =177 GPa。 解：方法 2：能量法： A B （外力功等于变形能） 60° （1）求钢索内力：以ABCD为研究对象： C P 400 800 XA A YA B T C T P D

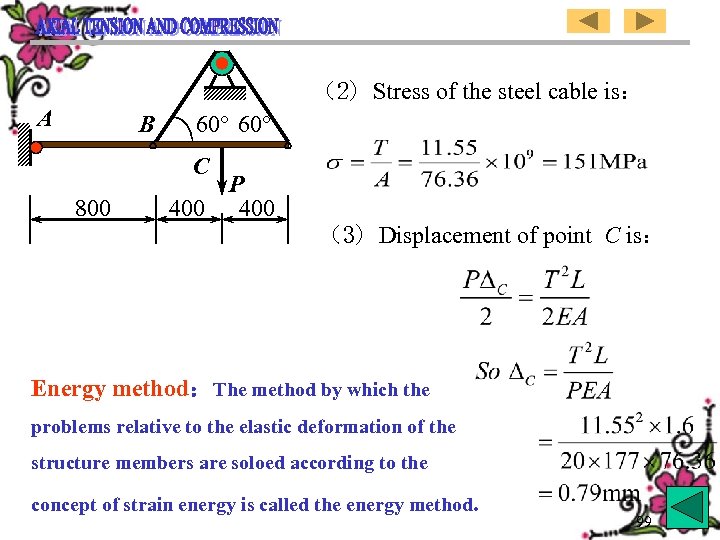（2) Stress of the steel cable is： A B 60° C 800 P 400 （3) Displacement of point C is： Energy method：The method by which the problems relative to the elastic deformation of the structure members are soloed according to the concept of strain energy is called the energy method. 99

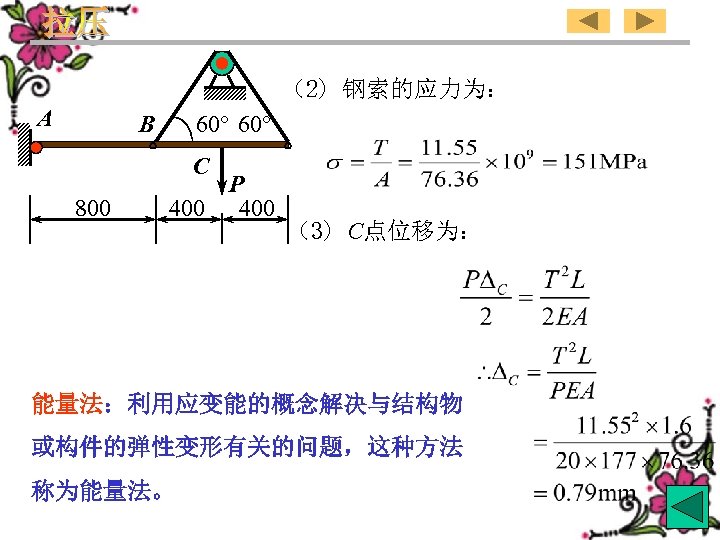（2) 钢索的应力为： A B 60° C 800 P 400 （3) C点位移为： 能量法：利用应变能的概念解决与结构物 或构件的弹性变形有关的问题，这种方法 称为能量法。

§ 1－6 STATICALLY INDETERMINATE PROBLEMS AND THEIR TREATMENT METHODS OF AXIAL TENSION AND COMPRESSION 1、Statically indeterminate problems and their treatment methods 1)、Statically indeterminate problems：The problems in which unknown forces(external forces、internal forces、stresses) cannot be wholly determined only by static equilibrium equations 2、Method to solve statically indeterminate problems： Equilibrium equations、compatibility equation of deformation and physical equations must be combined together to solve these problems. 101

§ 1－6 拉压超静定问题及其处理方法 一、超静定问题及其处理方法 1、超静定问题：单凭静力平衡方程不能确定出全部未知力 （外力、内力、应力）的问题。 2、超静定问题的处理方法：平衡方程、变形协调方程、 物理方程相结合，进行求解。

Example 10 Rods 1，2 and 3 are connected together with a pin as shown in the figure. Knowing the length of each rod is：L 1=L 2、 L 3 =L；and the area of each rod is A 1=A 2=A , A 3；modulus of elasticity of each rod is：E 1=E 2=E、 E 3. External force is along the upright direction. Determine the internal force of each rod. Solution： Equilibrium equations: B D C 3 1 2 A P N 3 N 1 N 2 A P 103

[例10] 设 1、2、3三杆用铰链连接如图，已知：各杆长为： L 1=L 2、 L 3 =L ；各杆面积为A 1=A 2=A、 A 3 ；各杆弹性模量 为：E 1=E 2=E、E 3。外力沿铅垂方向，求各杆的内力。 解： 、平衡方程: B D C 3 1 2 N 3 A P N 1 N 2 A P

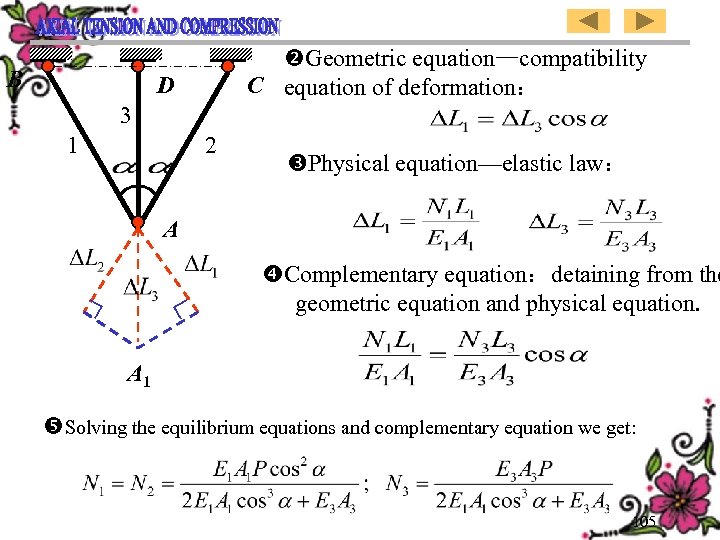B Geometric equation—compatibility C equation of deformation： D 3 1 2 Physical equation—elastic law： A Complementary equation：detaining from the geometric equation and physical equation. A 1 Solving the equilibrium equations and complementary equation we get: 105

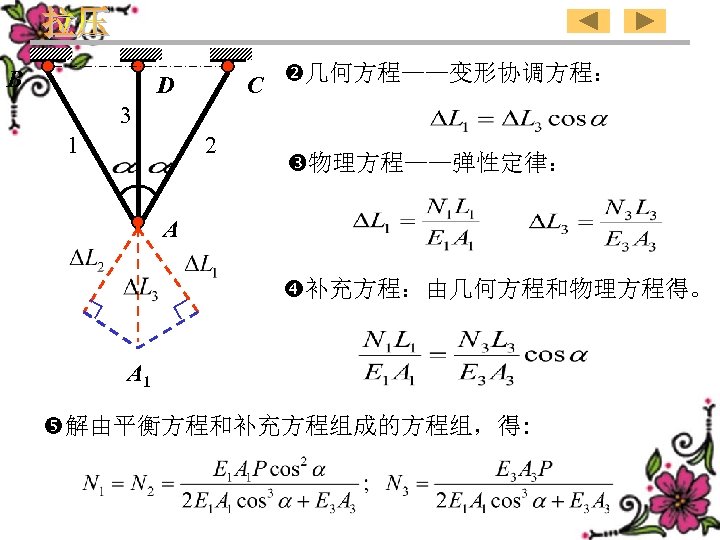B C 几何方程——变形协调方程： D 3 1 2 物理方程——弹性定律： A 补充方程：由几何方程和物理方程得。 A 1 解由平衡方程和补充方程组成的方程组，得:

3、Method and steps for solving statically indeterminate problems： Equilibrium equations； Geometric equation—compatibility equation of deformation； Physical equation—elastic law； Complementary equation：from geometric equation and physical equation Solving equilibrium equations and the complementary equation. 107

3、超静定问题的处理方法步骤： 平衡方程； 几何方程——变形协调方程； 物理方程——弹性定律； 补充方程：由几何方程和物理方程得； 解由平衡方程和补充方程组成的方程组。

Example 11 Four angles of a wooden pole are reinforced with four equal leg angle steel of 40 40 4. The allowable stresses of steel and wood are respectively [ ]1=160 MPa and [ ]2=12 MPa，module of elasticity of them are E 1=200 GPa and E 2=10 GPa. Respectively Determine the allowable permissible load P. Solution： Equilibrium P P y 4 N 1 N 2 equations: Geometric equation Physical equation and complementary equation： 109

[例11] 木制短柱的四角用四个 40 40 4的等边角钢加固，角钢 和木材的许用应力分别为[ ]1=160 M Pa和[ ]2=12 MPa，弹性模 量分别为E 1=200 GPa 和 E 2 =10 GPa；求许可载荷P。 P 解： 平衡方程: P y 4 N 1 N 2 几何方程 物理方程及补充方程：

P P 4 N 1 N 2 Solving equilibrium equations and y the complementary equation we get: Determine the permissible load of the structure： Method 1: Section area of the angle steel may be obtained from the table of hot-rolled steel: A 1=3. 086 cm 2 111

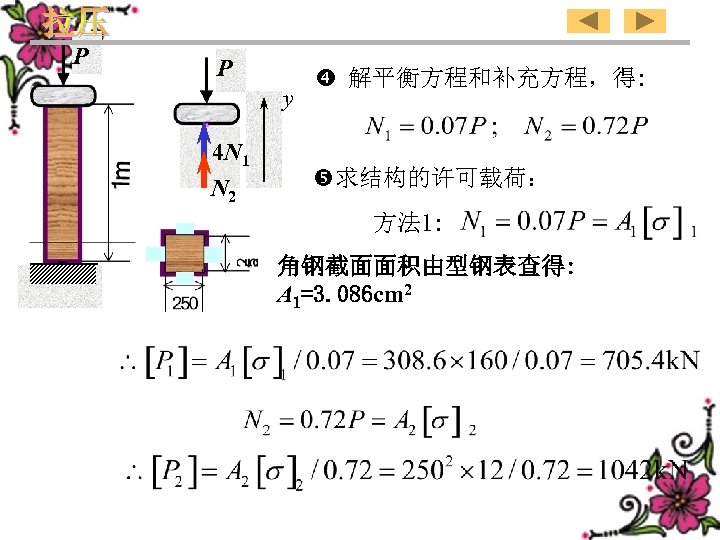P P y 4 N 1 N 2 解平衡方程和补充方程，得: 求结构的许可载荷： 方法 1: 角钢截面面积由型钢表查得: A 1=3. 086 cm 2

Determine the permissible load of the structure： Method 2: In the case of △ 1=△ 2，the angle steel will reach the limit state first, that is the maximum load is determined by the angle steel. Additionally：What about would it the like if area of the angle steel is increased as 5 times？ What about would it like if the area of the wood is changed into 25 mm 2? The maximum load of the structure is still controlled by the steel. 113

求结构的许可载荷： 方法 2: 所以在△ 1=△ 2 的前提下，角钢将先达到极限状态， 即角钢决定最大载荷。 另外：若将钢的面积增大 5倍，怎样？ 若将木的面积变为 25 mm 2，又怎样？ 结构的最大载荷永远由钢控制着。

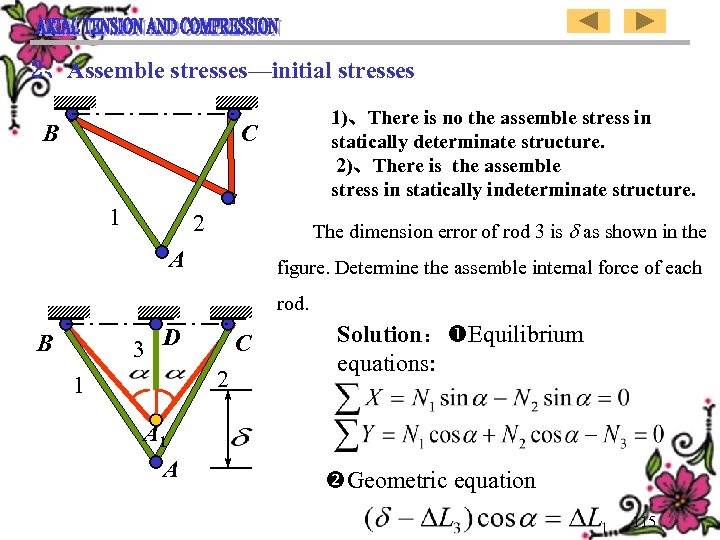2、Assemble stresses—initial stresses B 1)、There is no the assemble stress in statically determinate structure. 2)、There is the assemble stress in statically indeterminate structure. C 1 2 The dimension error of rod 3 is as shown in the A figure. Determine the assemble internal force of each rod. 3 D B C 2 1 A Solution： Equilibrium equations: Geometric equation 115

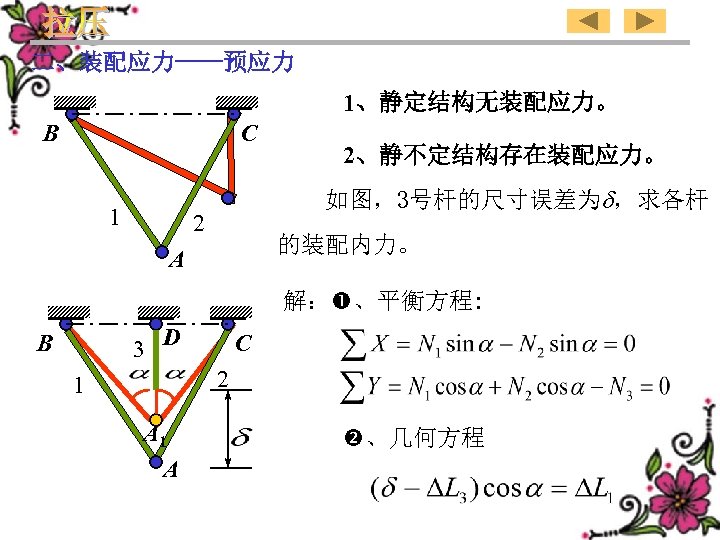二、装配应力——预应力 1、静定结构无装配应力。 B C 1 2、静不定结构存在装配应力。 如图，3号杆的尺寸误差为 ，求各杆 2 的装配内力。 A 解： 、平衡方程: 3 D B C 2 1 A 、几何方程

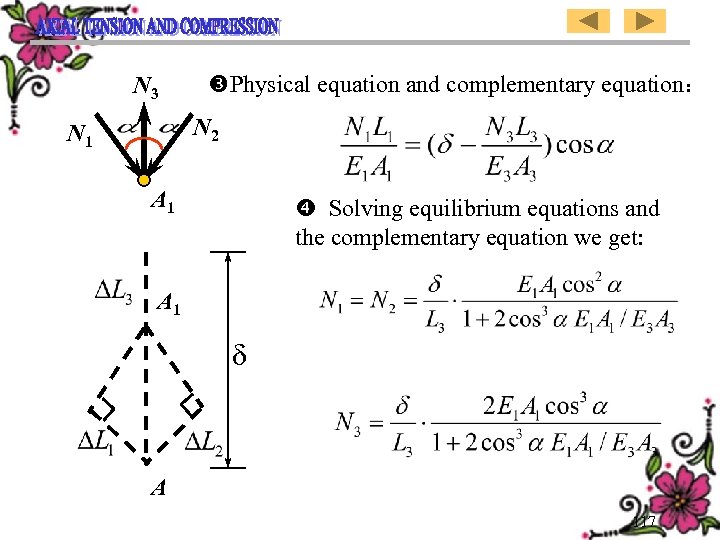N 3 Physical equation and complementary equation： N 2 N 1 A 1 Solving equilibrium equations and the complementary equation we get: A 1 d A 117

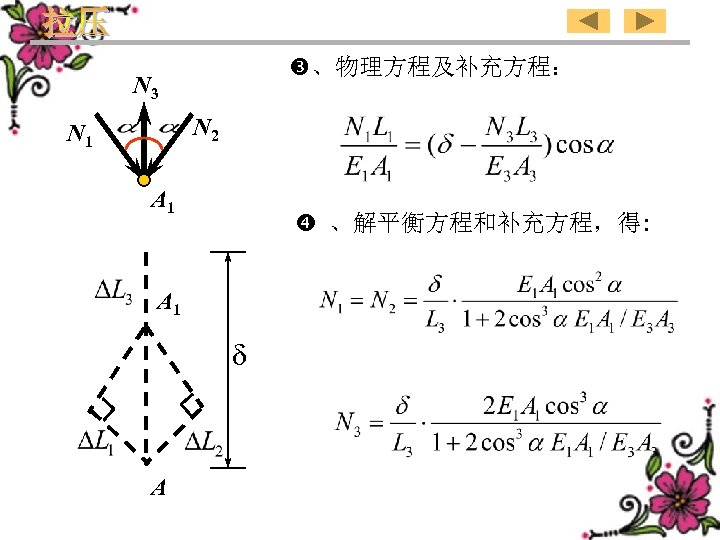、物理方程及补充方程： N 3 N 2 N 1 A 1 、解平衡方程和补充方程，得: A 1 d A

B 3、Temperature stress C 1 1)、There is no the temperature stress in statically determinate structure. 2)、There is the temperature stress in statically indeterminate structure. 2 A B D C 3 1 2 Materials and dimensions of rod 1 and 2 are all the same as shown in the figure. If temperature of the structure changes from T 1 to T 2, determine the A temperature internal forces of each rod. （linear thermal expansion coefficient of each rod i ; △T= T 2 -T 1) A 1 119

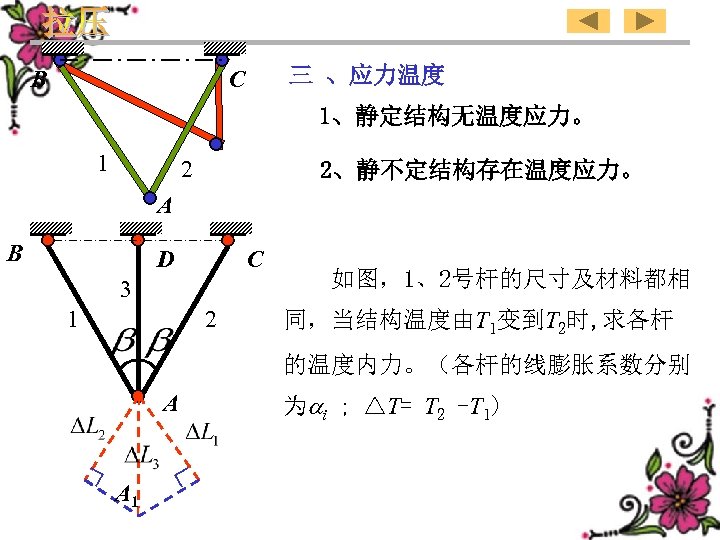B 三 、应力温度 C 1、静定结构无温度应力。 1 2 2、静不定结构存在温度应力。 A B D C 3 1 2 如图，1、2号杆的尺寸及材料都相 同，当结构温度由T 1变到T 2时, 求各杆 的温度内力。（各杆的线膨胀系数分别 A A 1 为 i ; △T= T 2 -T 1)

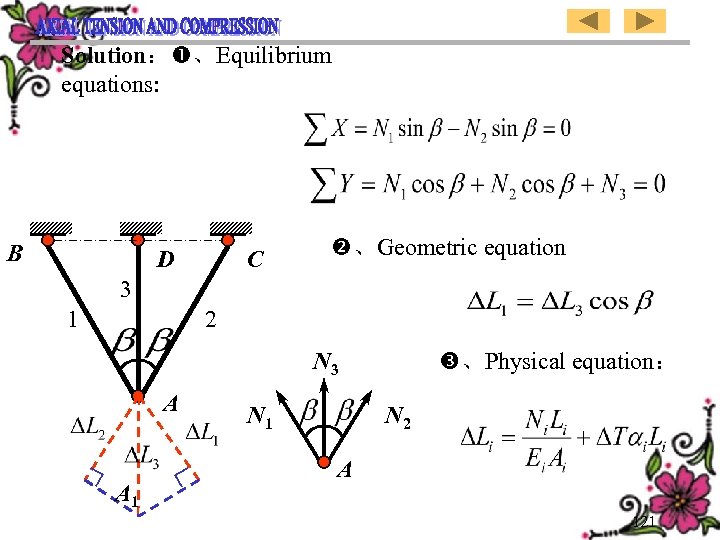Solution： 、Equilibrium equations: B D C 、Geometric equation 3 1 2 、Physical equation： N 3 A A 1 N 2 A 121

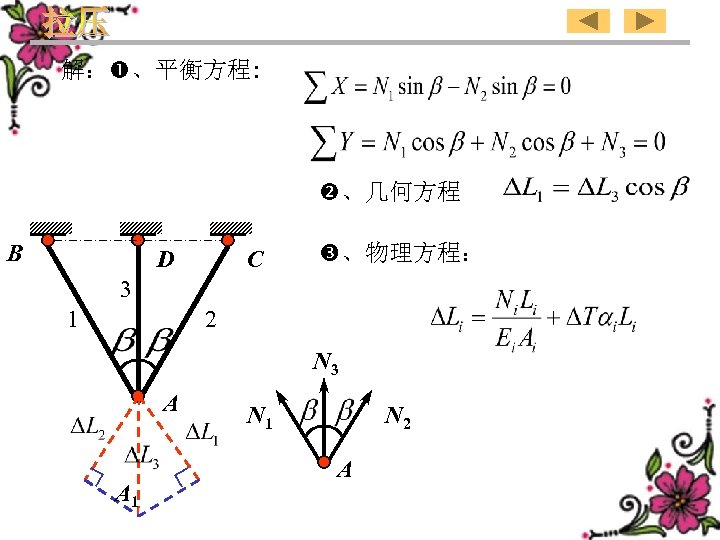解： 、平衡方程: 、几何方程 B D C 、物理方程： 3 1 2 N 3 A A 1 N 2 A

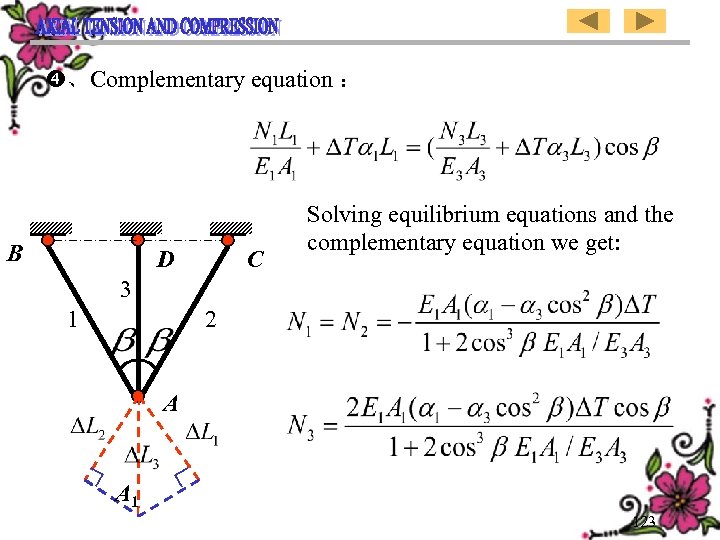、Complementary equation ： B D C Solving equilibrium equations and the complementary equation we get: 3 1 2 A A 1 123

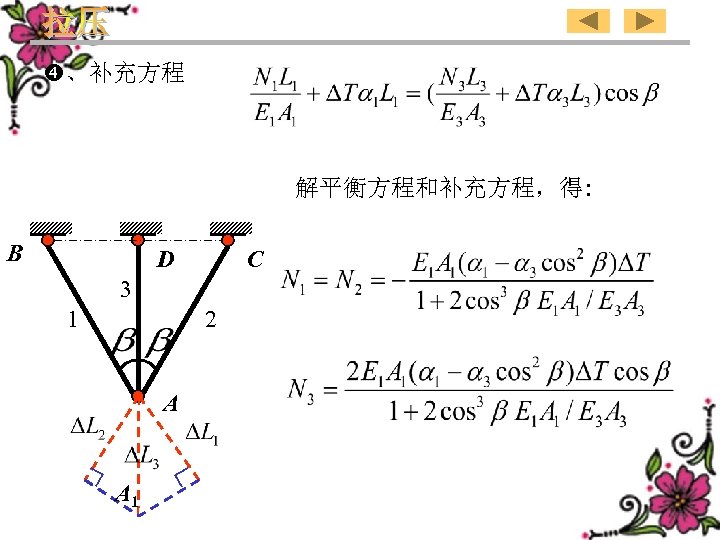、补充方程 解平衡方程和补充方程，得: B D C 3 1 2 A A 1

a Example 12 Theupper and lower ends of a ladder-like steel shaft are fixed at temperature T 1=5℃ as shown in the figure. Areas of the upper and lower segments are respectively 1= cm 2 a and 2= cm 2. When its temperature reaches T 2=25℃, determine the temperature stress of each rod. (Linear thermal expansion coefficient N 1 a E=200 GPa) a N 2 = 2. 5× 10 -6 1/0 C；modulus of elasticity Solution： 、Equilibrium equation ： 、Geometric equation： 125

a [例12] 如图，阶梯钢杆的上下两端在T 1=5℃ 时被固定, 杆的上下两段的面积分别 a = cm 2 ， = cm 2，当温度升至T 2 =25℃时, 求各杆的温度应力。 (线膨胀系数 =12. 5× 弹性模量E=200 GPa) N 1 a 解： 、平衡方程： a 、几何方程： N 2 ；

、Physical equation : 、Complementary equation : Solving equilibrium equations and the complementary equation we get: 、Temperature stresses : 127

、物理方程 、补充方程 解平衡方程和补充方程，得: 、温度应力

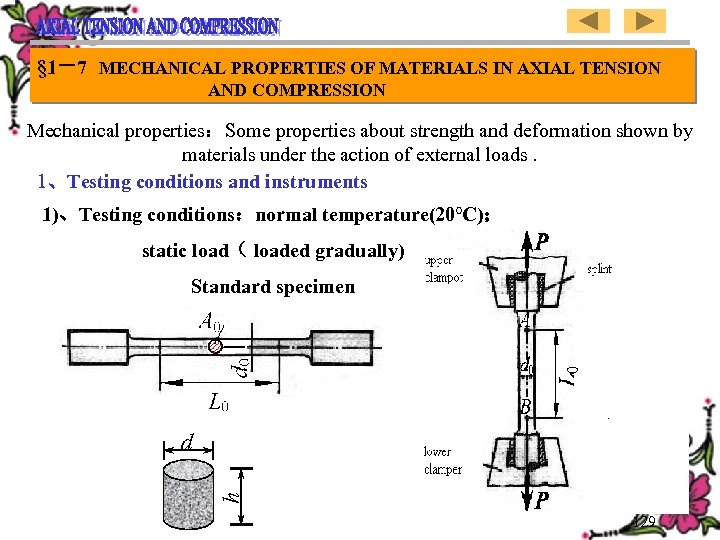§ 1－7 MECHANICAL PROPERTIES OF MATERIALS IN AXIAL TENSION AND COMPRESSION Mechanical properties：Some properties about strength and deformation shown by materials under the action of external loads. 1、Testing conditions and instruments 1)、Testing conditions：normal temperature(20℃)； static load（ loaded gradually) Standard specimen h d 129

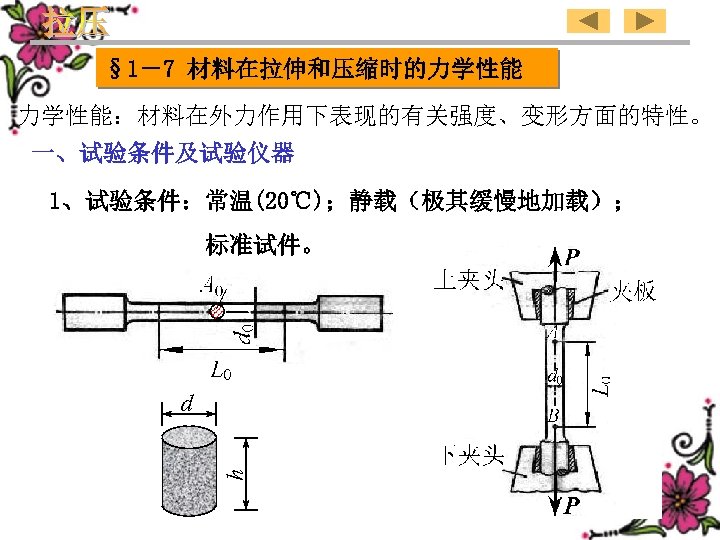§ 1－7 材料在拉伸和压缩时的力学性能：材料在外力作用下表现的有关强度、变形方面的特性。 一、试验条件及试验仪器 1、试验条件：常温(20℃)；静载（极其缓慢地加载）； 标准试件。 h d

2、Experimental implement：Universal testing machine ；Extensometer 131

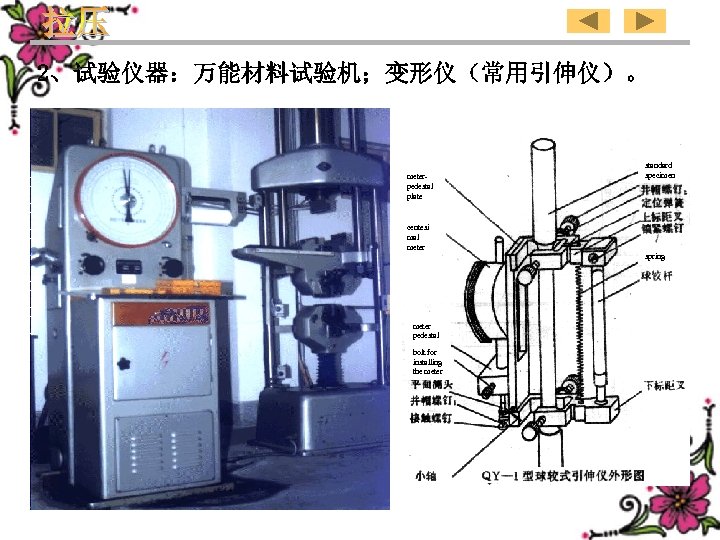2、试验仪器：万能材料试验机；变形仪（常用引伸仪）。 meterpedestal plate standard specimen centesi mal meter spring meter pedestal bolt for installing the meter

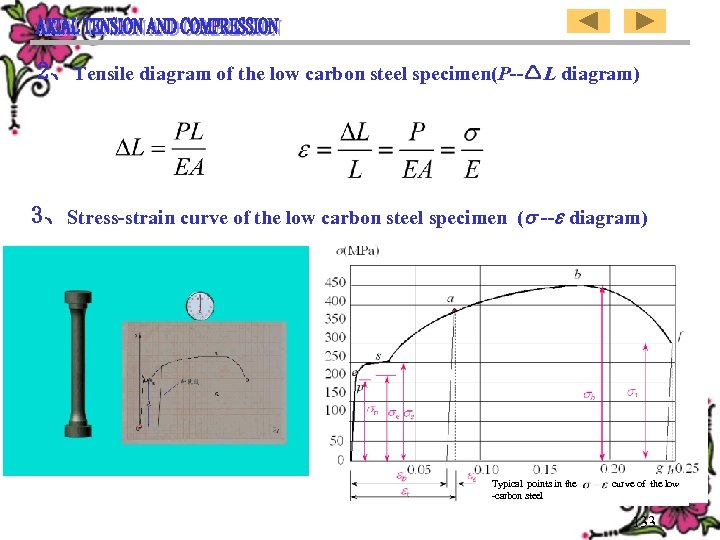2、Tensile diagram of the low carbon steel specimen(P-- L diagram) 3、Stress-strain curve of the low carbon steel specimen ( -- diagram) Typical points in the -carbon steel curve of the low 133

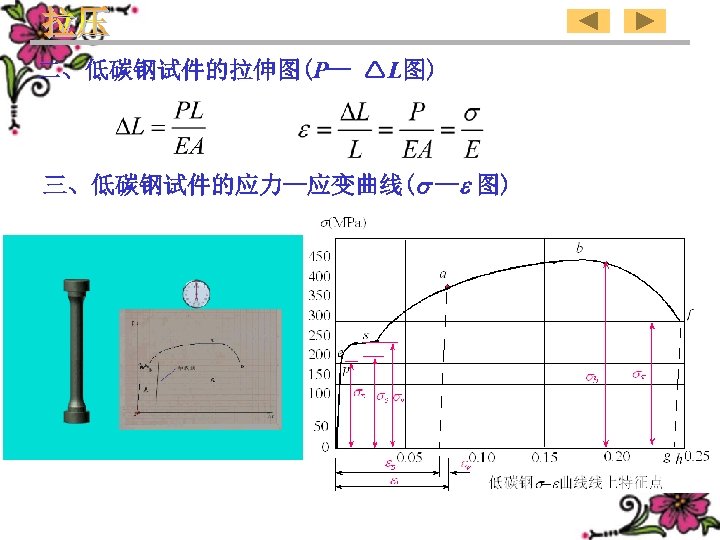二、低碳钢试件的拉伸图(P-- L图) 三、低碳钢试件的应力--应变曲线( -- 图)

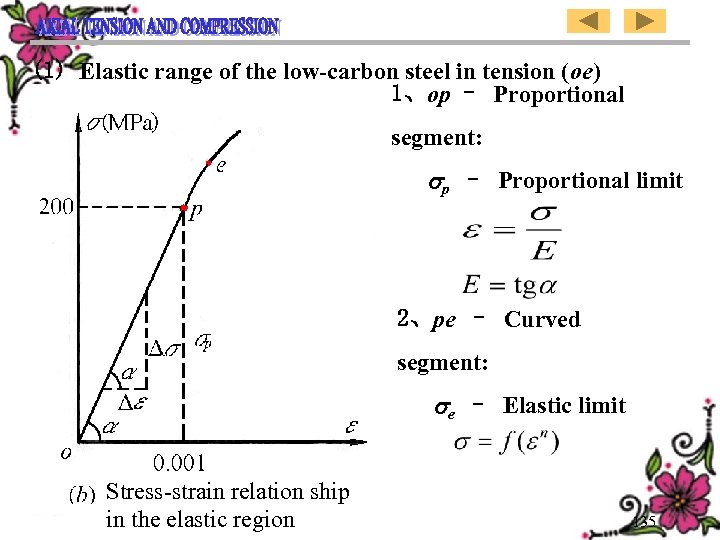(1) Elastic range of the low-carbon steel in tension (oe) 1、op – Proportional segment: p – Proportional limit 2、pe – Curved segment: e – Elastic limit Stress-strain relation ship in the elastic region 135

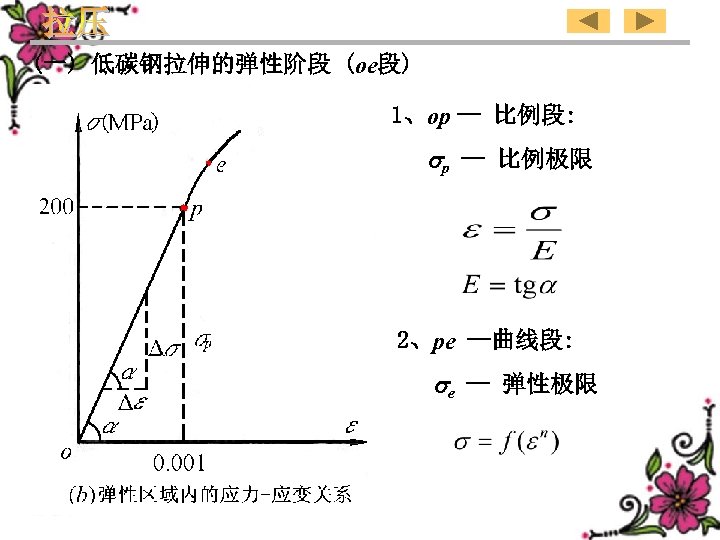(一) 低碳钢拉伸的弹性阶段 (oe段) 1、op -- 比例段: p -- 比例极限 2、pe --曲线段: e -- 弹性极限

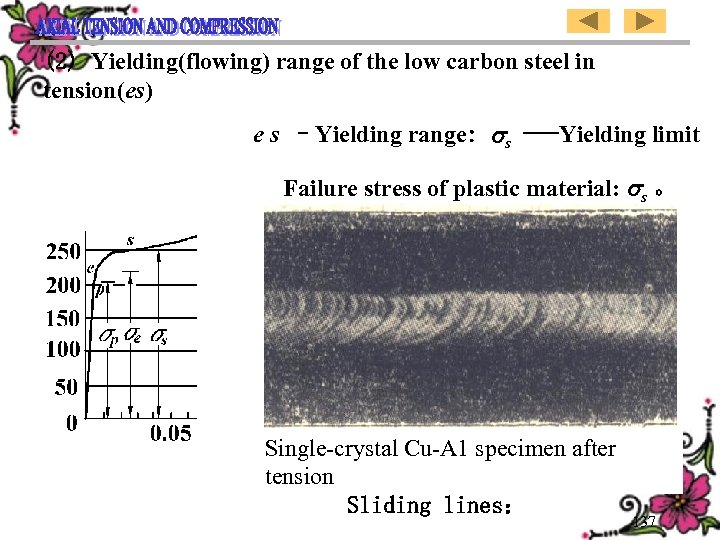(2) Yielding(flowing) range of the low carbon steel in tension(es) e s –Yielding range: s ---Yielding limit Failure stress of plastic material: s 。 Single-crystal Cu-A 1 specimen after tension Sliding lines： 137

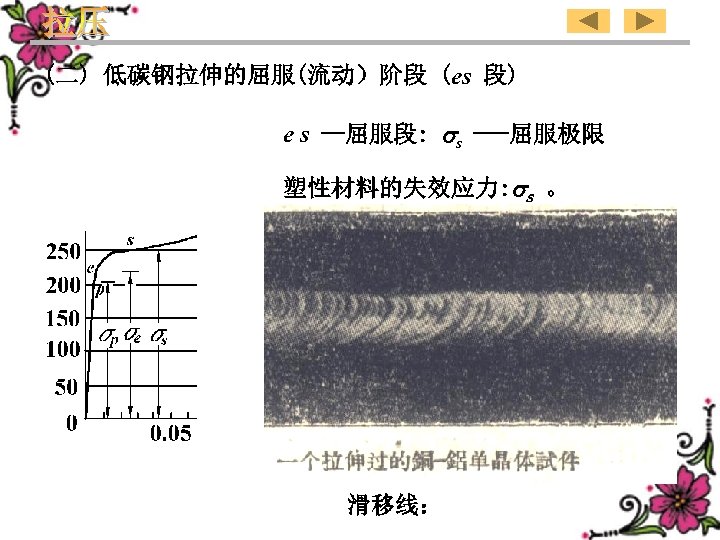(二) 低碳钢拉伸的屈服(流动）阶段 (es 段) e s --屈服段: s ---屈服极限 塑性材料的失效应力: s 。 滑移线：

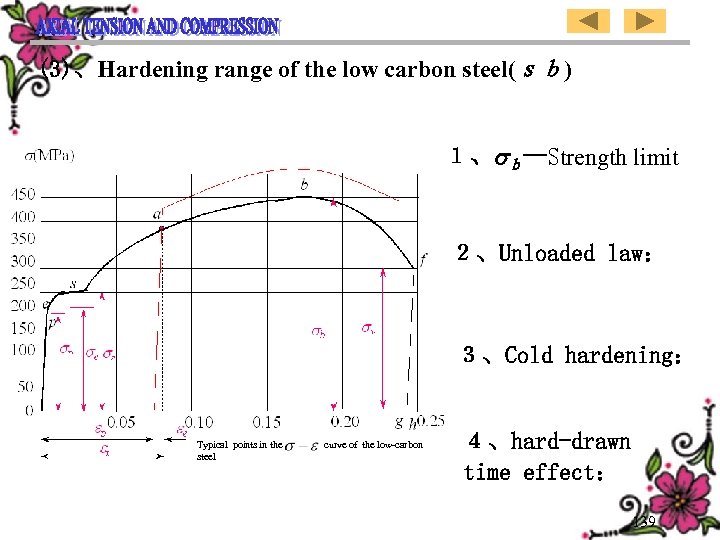(3)、Hardening range of the low carbon steel(ｓｂ) １、 ｂ--Strength limit ２、Unloaded law： ３、Cold hardening： Typical points in the steel curve of the low-carbon ４、hard-drawn time effect： 139

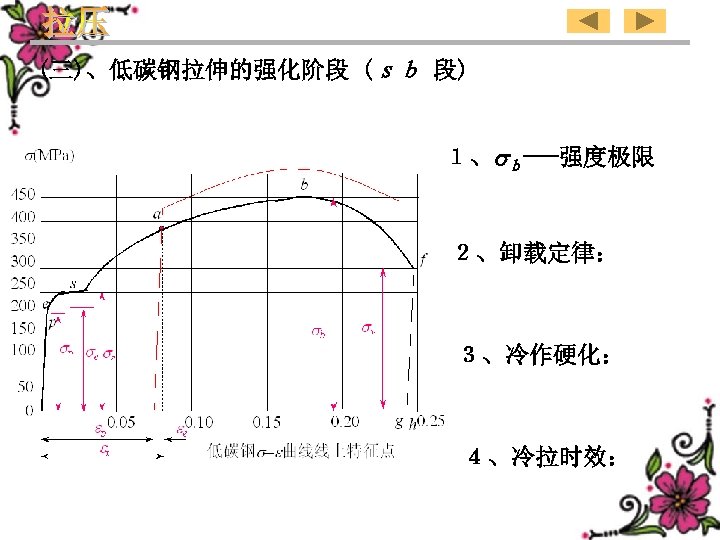(三)、低碳钢拉伸的强化阶段 (ｓｂ 段) １、 ｂ---强度极限 ２、卸载定律： ３、冷作硬化： ４、冷拉时效：

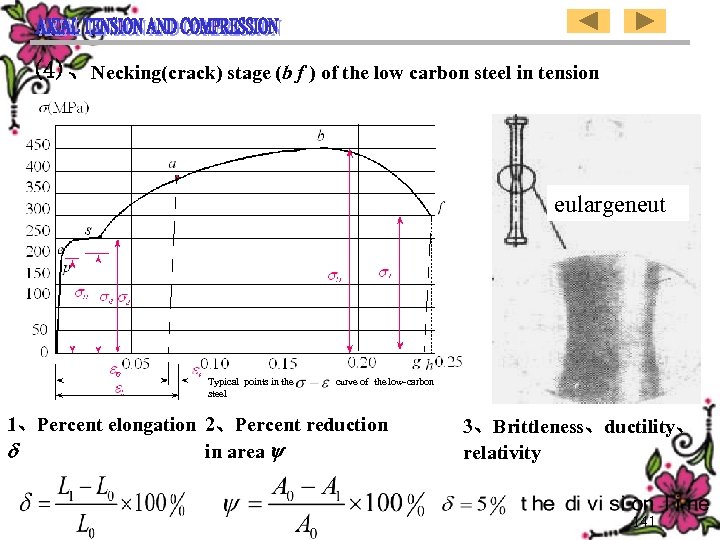(4)、Necking(crack) stage (b f ) of the low carbon steel in tension eulargeneut Typical points in the steel curve of the low-carbon 1、Percent elongation 2、Percent reduction in area 3、Brittleness、ductility、 relativity 141

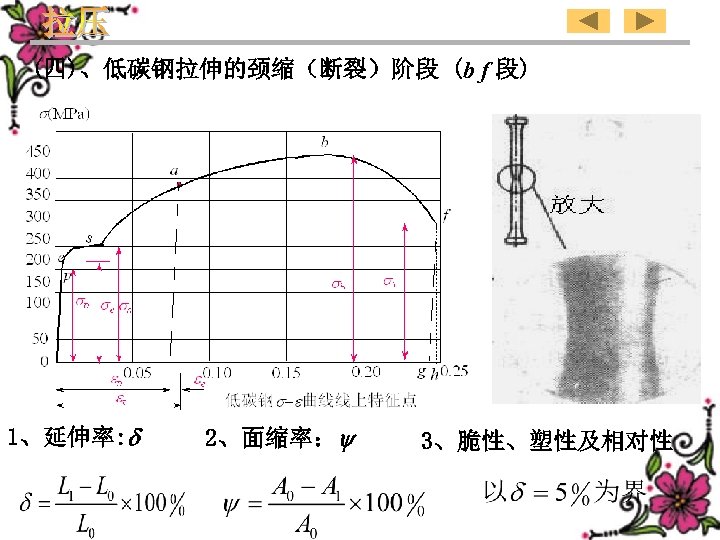(四)、低碳钢拉伸的颈缩（断裂）阶段 (b f 段) 1、延伸率: 2、面缩率： 3、脆性、塑性及相对性

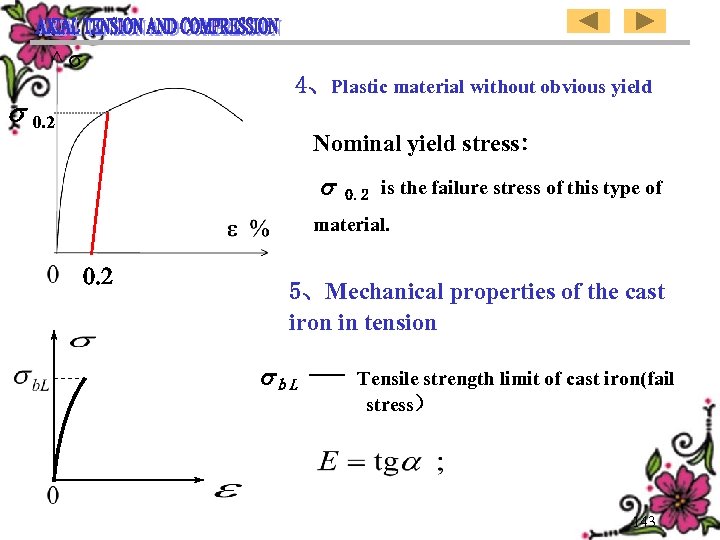4、Plastic material without obvious yield 0. 2 Nominal yield stress: 0. 2 is the failure stress of this type of material. 0. 2 5、Mechanical properties of the cast iron in tension ｂL --- Tensile strength limit of cast iron(fail stress） 143

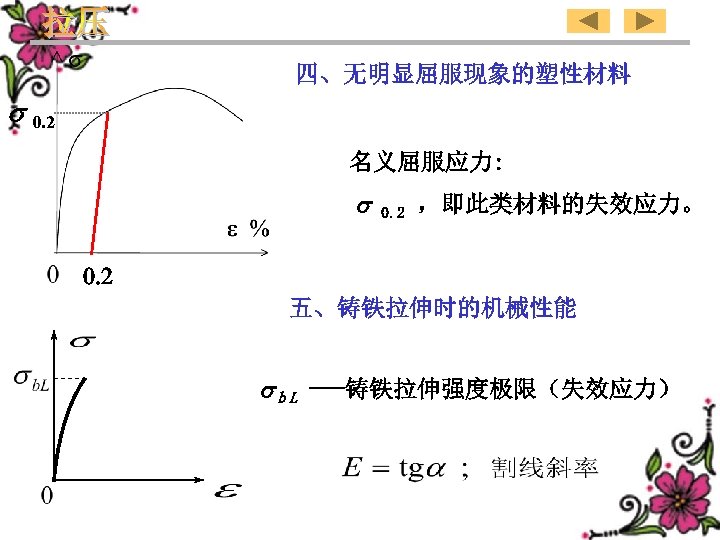四、无明显屈服现象的塑性材料 0. 2 名义屈服应力: 0. 2 ，即此类材料的失效应力。 0. 2 五、铸铁拉伸时的机械性能 ｂL ---铸铁拉伸强度极限（失效应力）

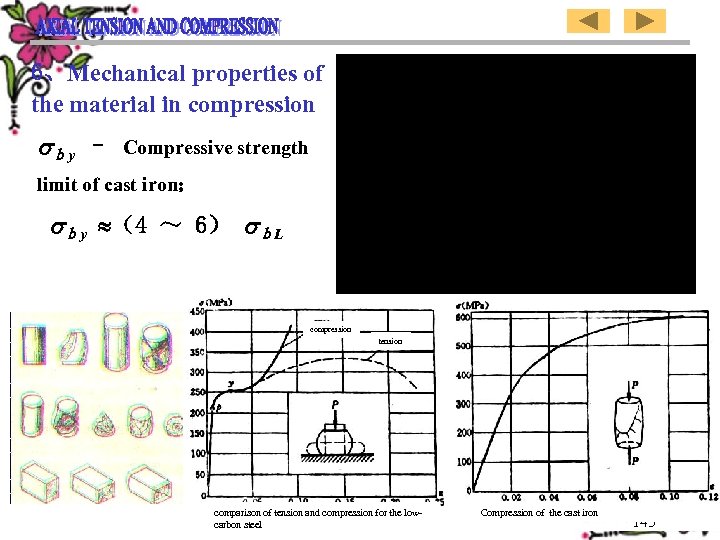6、Mechanical properties of the material in compression ｂy – Compressive strength limit of cast iron； ｂy （4 ～ 6） ｂL compression tension comparison of tension and compression for the lowcarbon steel Compression of the cast iron 145

六、材料压缩时的机械性能 ｂy ---铸铁压缩强度极限； ｂy （4 ～ 6） ｂL

7、Safety factor、permissible stress、limit stress 1)、Permissible stress： 2)、Limit stress： 3)、 Safety factor： N>1 147

七、安全系数、许用应力、极限应力 1、 许用应力： 2、极限应力： 3、安全系数： N>1

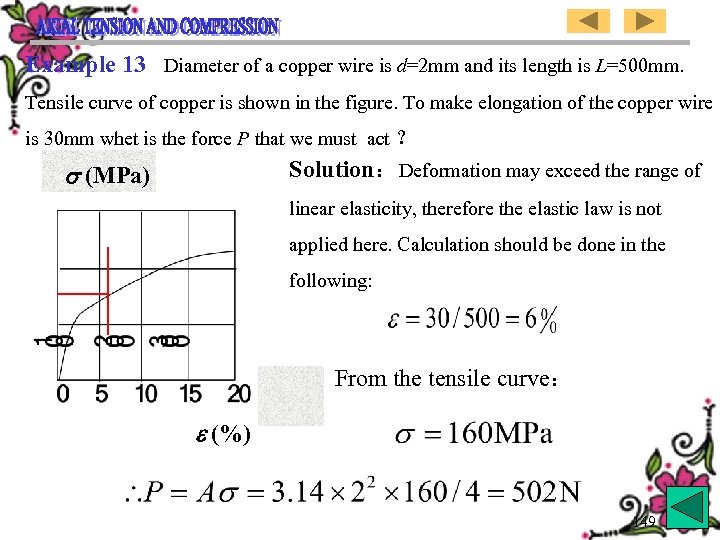Example 13 Diameter of a copper wire is d=2 mm and its length is L=500 mm. Tensile curve of copper is shown in the figure. To make elongation of the copper wire is 30 mm whet is the force P that we must act ？ Solution：Deformation may exceed the range of (MPa) linear elasticity, therefore the elastic law is not applied here. Calculation should be done in the following: From the tensile curve： (%) 149

[例13] 铜丝直径d=2 mm，长L=500 mm， 材料的拉伸曲线如图 所示。如欲使铜丝的伸长量为 30 mm， 则大约需加多大的力P？ (MPa) 解：变形量可能已超出了“线弹性”范 围，故，不可再应用“弹性定律”。应 如下计算： 由拉伸图知： (%)