Measuring Motion Chapter 1 section 1 pages 4

Measuring Motion Chapter 1 section 1 pages 4 -9 Vocabulary: Motion, Speed, Velocity and Acceleration

Motion p. 4 Reference Point: Something that appears to stay in place When an object changes position over time relative to a reference point, the object is in motion.

Speed Page 5 Speed is the rate of motion, often expressed as distance traveled per unit of time. Total Distance average speed = ---------Total Time Your driving up with the family and you’ve been on the road for 2 hours. You’ve traveled 130 miles. What is your average speed? Answer: 65 miles / hour

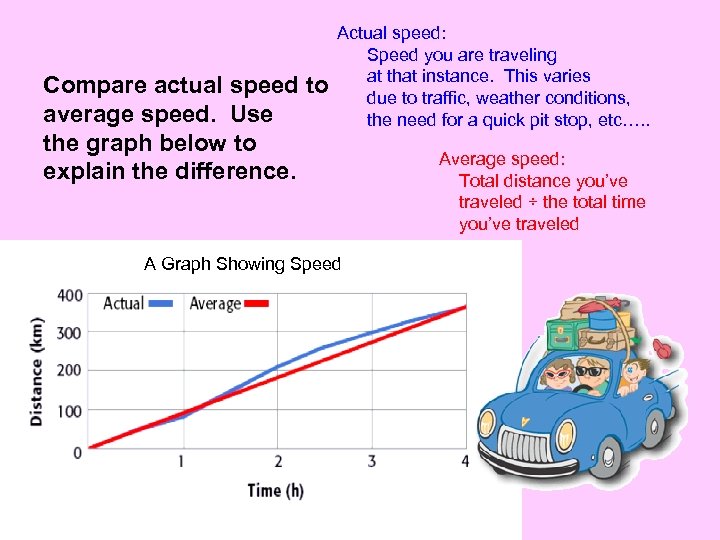Compare actual speed to average speed. Use the graph below to explain the difference. Actual speed: Speed you are traveling at that instance. This varies due to traffic, weather conditions, the need for a quick pit stop, etc…. . A Graph Showing Speed Average speed: Total distance you’ve traveled ÷ the total time you’ve traveled

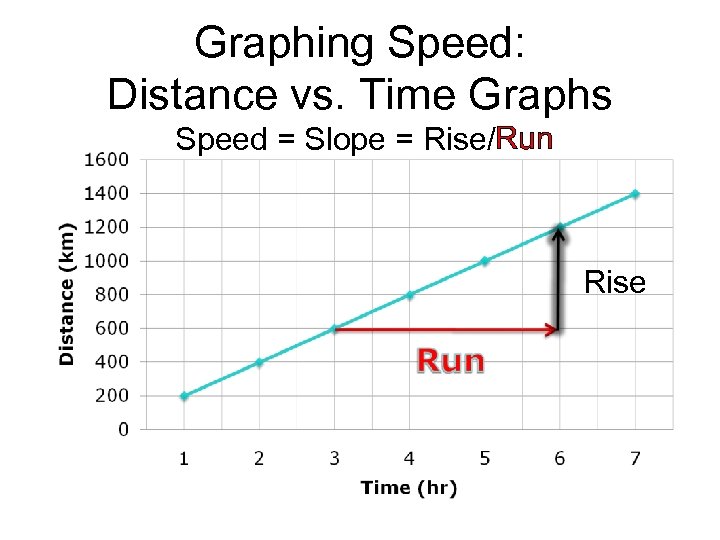Graphing Speed: Distance vs. Time Graphs Speed = Slope = Rise/Run Rise

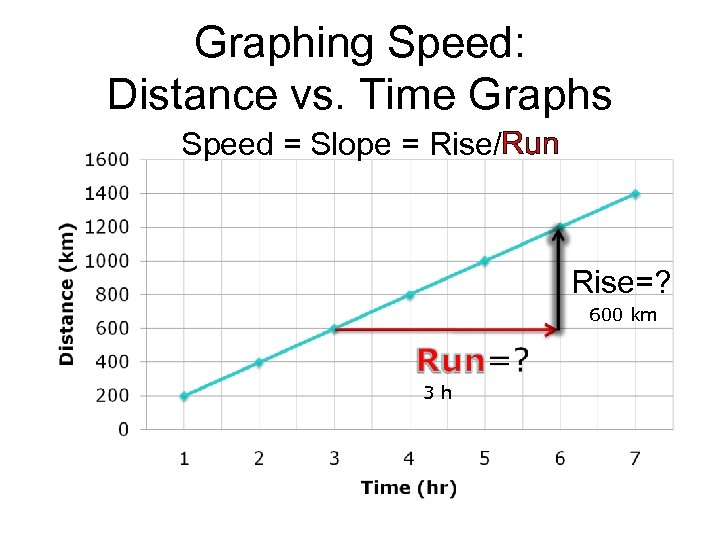Graphing Speed: Distance vs. Time Graphs Speed = Slope = Rise/Run Rise=? 600 km 3 h

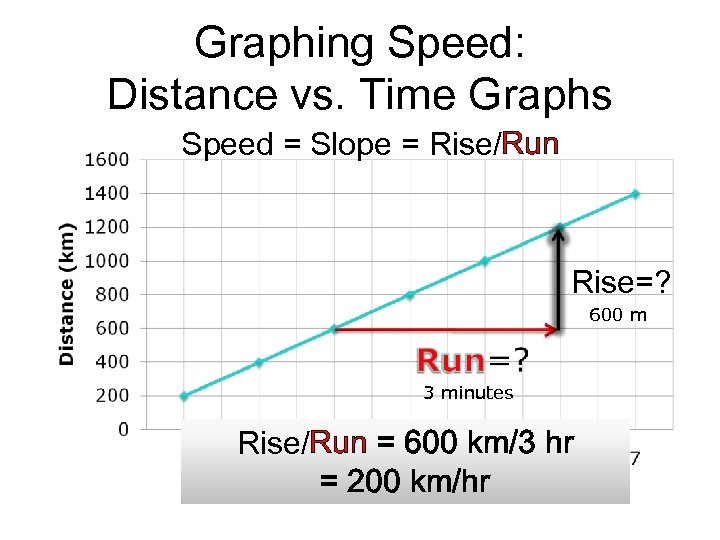Graphing Speed: Distance vs. Time Graphs Speed = Slope = Rise/Run Rise=? 600 m 3 minutes Rise/Run = 600 km/3 hr = 200 km/hr

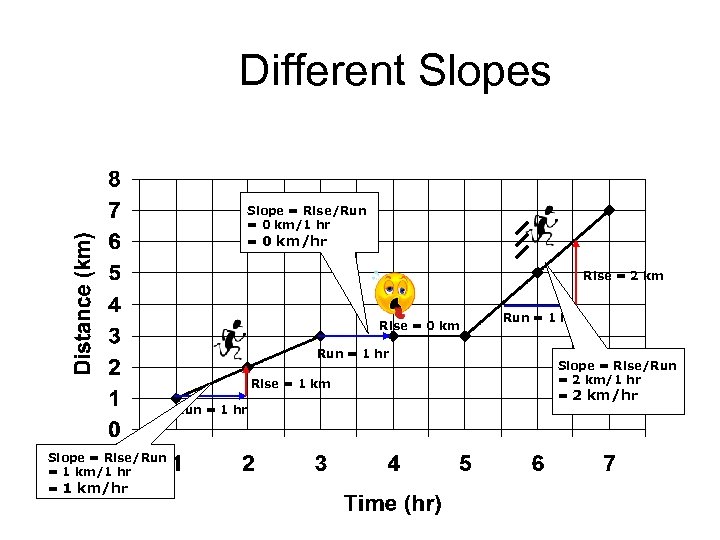Different Slopes Slope = Rise/Run = 0 km/1 hr = 0 km/hr Rise = 2 km Rise = 0 km Run = 1 hr Rise = 1 km Run = 1 hr Slope = Rise/Run = 1 km/1 hr = 1 km/hr Run = 1 hr Slope = Rise/Run = 2 km/1 hr = 2 km/hr

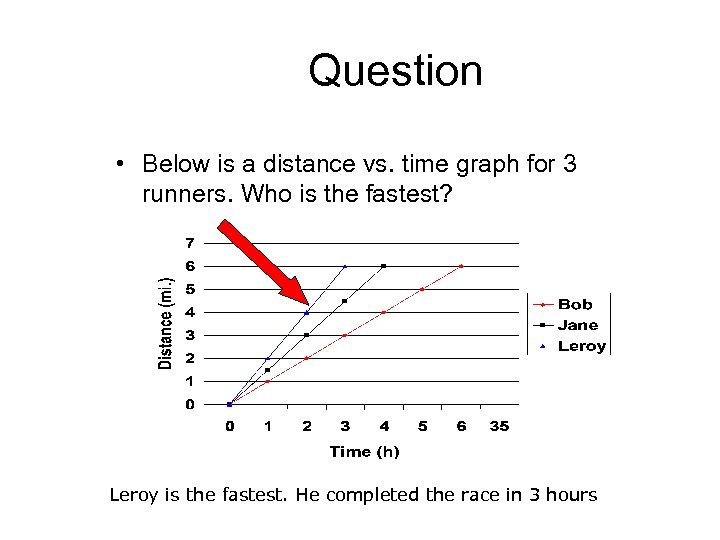Question • Below is a distance vs. time graph for 3 runners. Who is the fastest? Leroy is the fastest. He completed the race in 3 hours

Calculating Average Speed

• • When objects will move at a steady rate with a constant speed, the object will cover the same distance every regular interval of time. For instance, a cross-country runner might be running with a constant speed of 6 m/s in a straight line for several minutes. If her speed is constant, then the distance traveled every second is the same. The runner would cover a distance of 6 meters every second. If we could measure her position (distance from an arbitrary starting point) each second, then we would note that the position would be changing by 6 meters each second. This would be in stark contrast to an object that is changing its speed. An object with a changing speed would be moving a different distance each second. The data tables below depict objects with constant and changing speed. http: //www. physicsclassroom. com/mmedia/kinema/avd. cfm

Velocity p. 6 The speed of an object in a particular direction You and a friend raced back to your house. You both traveled at the same speed, but you got there first. Why? You took the direct route “straight line” to the house. When speed and direction remains the same, it’s known as “constant velocity. ”

What are the 2 ways that velocity can change? By changing Speed and/or Direction p. 6

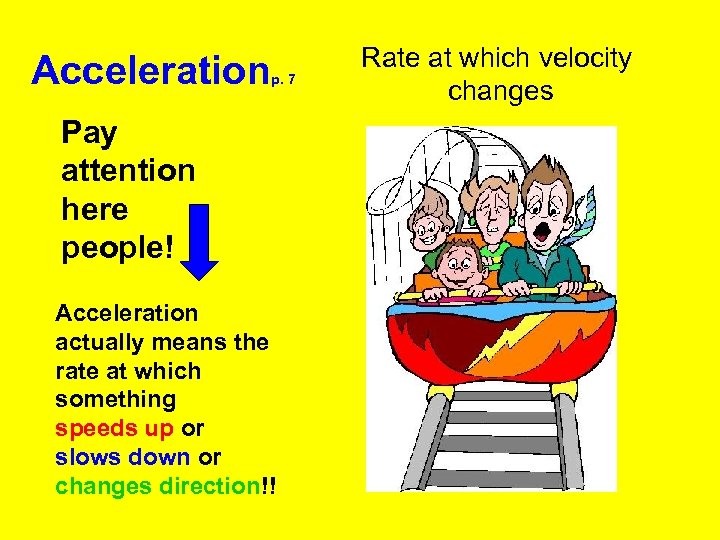Acceleration p. 7 Pay attention here people! Acceleration actually means the rate at which something speeds up or slows down or changes direction!! Rate at which velocity changes

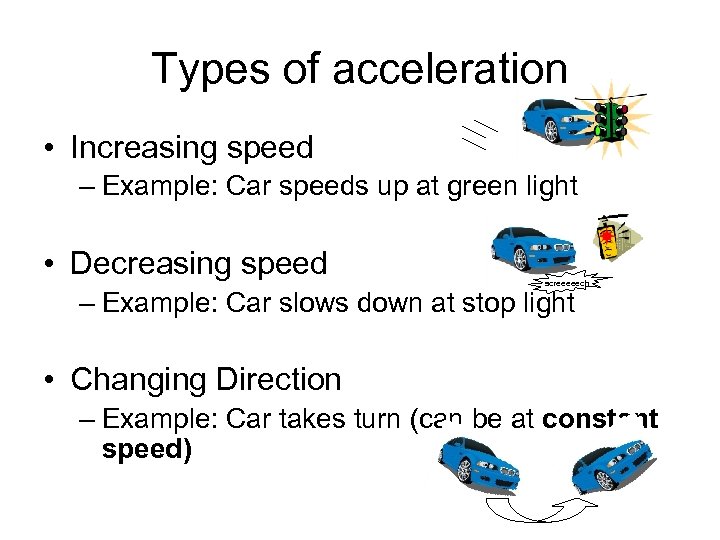Types of acceleration • Increasing speed – Example: Car speeds up at green light • Decreasing speed screeeeech – Example: Car slows down at stop light • Changing Direction – Example: Car takes turn (can be at constant speed)

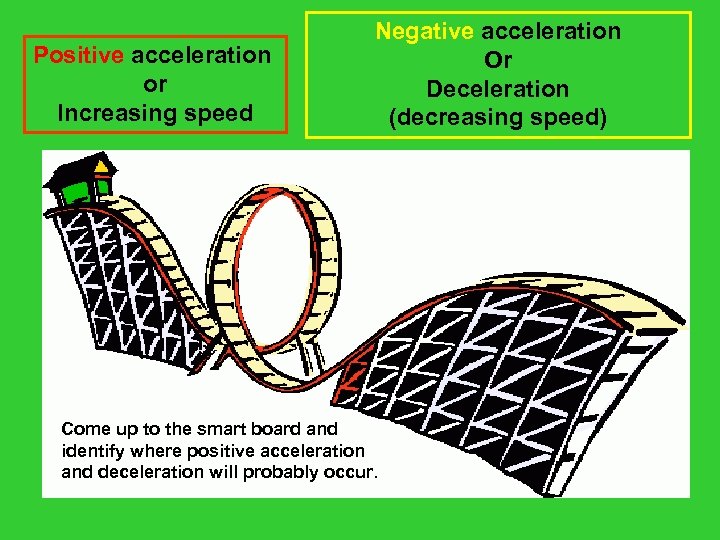Positive acceleration or Increasing speed Negative acceleration Or Deceleration (decreasing speed) Come up to the smart board and identify where positive acceleration and deceleration will probably occur.

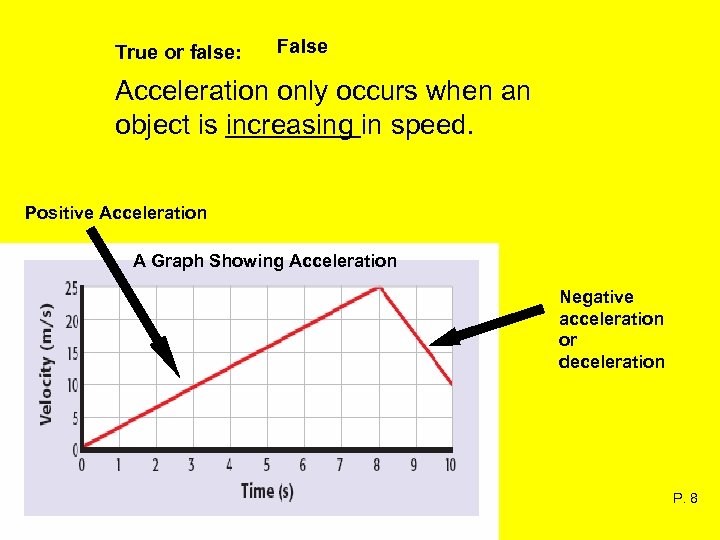True or false: False Acceleration only occurs when an object is increasing in speed. Positive Acceleration A Graph Showing Acceleration Negative acceleration or deceleration P. 8

Question • How can a car be accelerating if its speed is a constant 65 km/h? • If it is changing directions it is accelerating

Graphing Acceleration • Can use 2 kinds of graphs – Speed vs. time – Distance vs. time

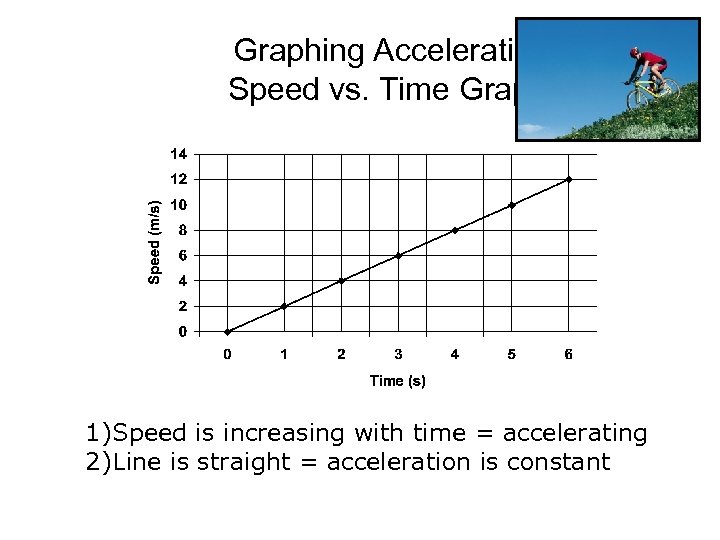Graphing Acceleration: Speed vs. Time Graphs 1)Speed is increasing with time = accelerating 2)Line is straight = acceleration is constant

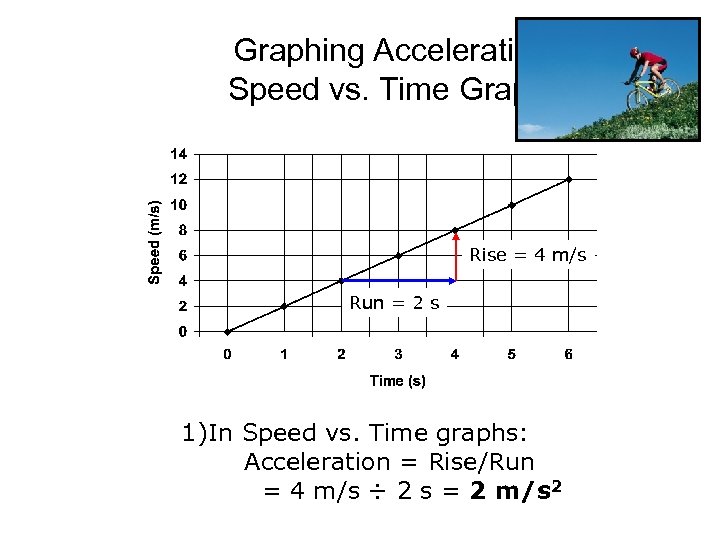Graphing Acceleration: Speed vs. Time Graphs Rise = 4 m/s Run = 2 s 1)In Speed vs. Time graphs: Acceleration = Rise/Run = 4 m/s ÷ 2 s = 2 m/s 2

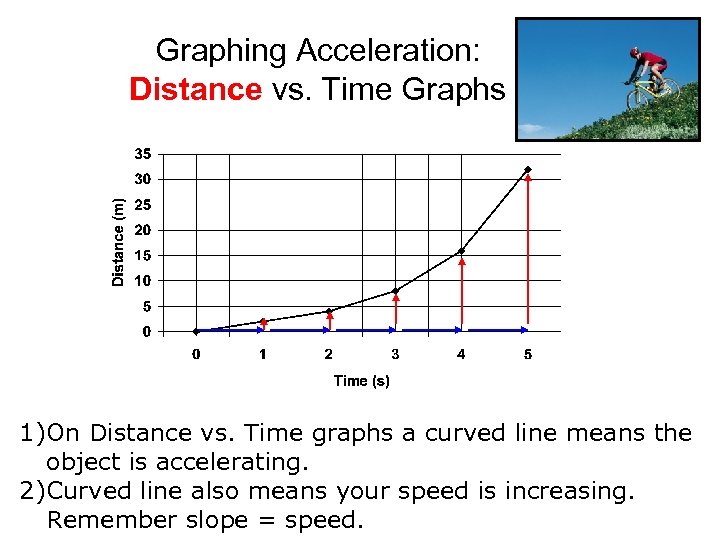Graphing Acceleration: Distance vs. Time Graphs 1)On Distance vs. Time graphs a curved line means the object is accelerating. 2)Curved line also means your speed is increasing. Remember slope = speed.

Centripetal Acceleration that occurs in a circular motion p. 9

Section Summary p. 9 • An object is in motion if it changes position over time in relation to a reference point. • Speed is the distance traveled by an object divided (speed = distance ÷ time) by the time the object takes to travel that distance. • Velocity is speed in a given direction. • Acceleration is the rate at which velocity changes. • An object can accelerate by changing speed, direction, or both. • Speed can be represented on a graph of distance versus time. • Acceleration can be represented by; graphing velocity versus time. • Acceleration that occurs in circular motion is known as centripetal acceleration.

See you at the finish line!