Measuring Matter-A Common Language A Standard Measurement

Measuring Matter-A Common Language

A Standard Measurement System The International System of Units (SI)

The Metric System

When and why was the metric system invented? • The metric system was invented by a group of French scientists in 1790 • The metric system was invented because countries were using many different systems of measurement causing confusion and lack of consistency

WHY DO WE USE THE METRIC SYSTEM? • Almost all other countries are using the metric system • Other countries’ companies are refusing to buy products from the U. S. if not labeled in metric units * Scientists need a universal way to communicate data (SI Units)

WHAT DOES THE METRIC SYSTEM MEASURE? * The gram measures mass or how much something weighs * The liter measures volume which is used when measuring liquids * The meter measures the length of an object or the distance from place to place

Scientists all over the world use the International System of Units to measure: • • • Length Volume Mass Density Temperature Time

Metric System A system of measurement used by the majority of countries on Earth based on the number 10

Key Concept: Why do scientists use a standard measurement system? • Using SI as the standard system of measurement allows scientists to compare data and communicate with each other about their results • Using SI measurement also allows experiments to be repeated and most importantly achieve a desired result

DRAW THE FOLLOWING CHART ON THE BLANK SHEET OF WHITE PAPER IN THE REFERENCE PART OF YOUR FOLDER

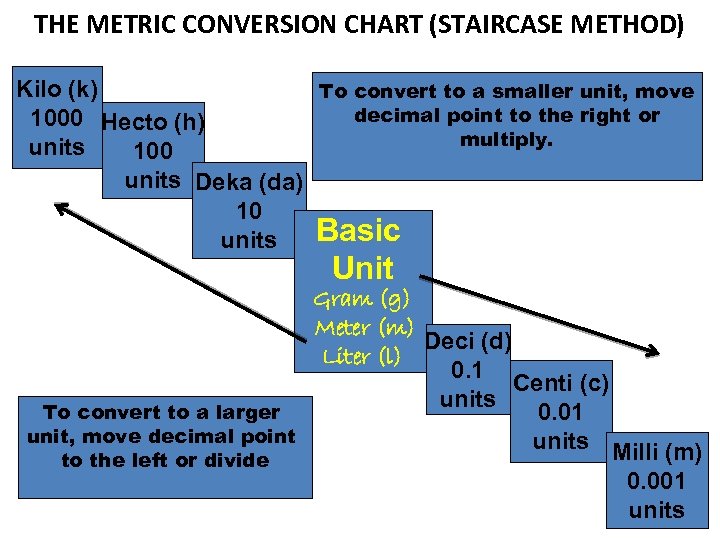
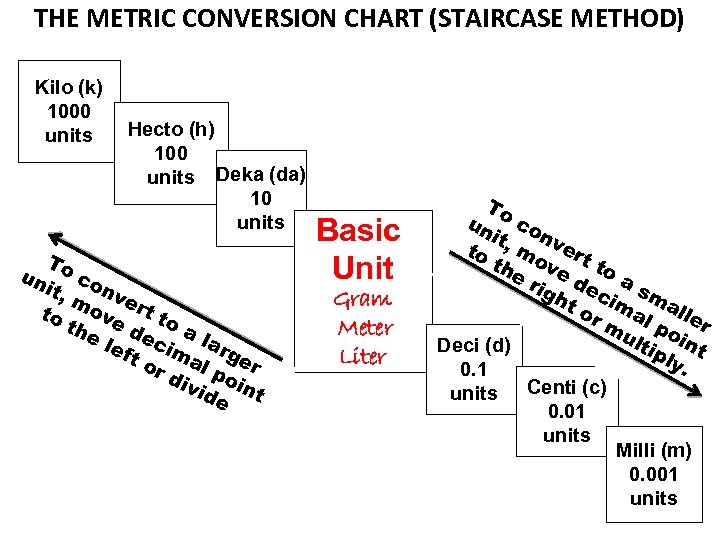THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo (k) 1000 units Hecto (h) 100 units Deka (da) 10 units To un c it, onv m e to ove rt to th e l dec a la eft im r al ger or div poi ide nt Basic Unit Gram Meter Liter To un co n it to , mo vert th e r ve d to a igh ec sm t o ima al r m l p ler ult oin Deci (d) ipl t y. 0. 1 units Centi (c) 0. 01 units Milli (m) 0. 001 units

Length

Figure 1: Calculating - How much larger is a kilo- than a deka-? • 100 times

What is length? • Length is the distance from one point to another

What tool do we use to measure length or distance?

A METER STICK is used to measure lengths and distances

METER STICK

The basic unit of length in the SI system is the … METER

APPROXIMATE CONVERSIONS BETWEEN METRIC & US LENGTH UNITS • A meter is about the same length as a yard • A meter is about three feet long • A decimeter is about four inches long • An inch is about 25 millimeters • A foot contains about 30 centimeters • A foot contains about 3 decimeters

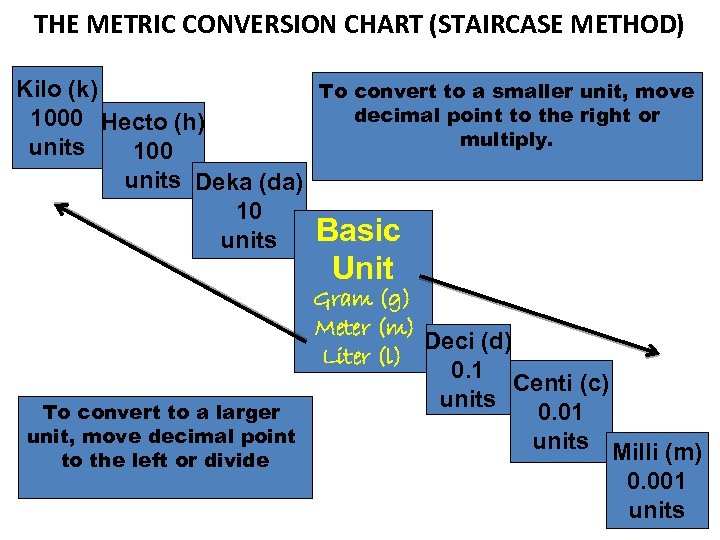THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo (k) To convert to a smaller unit, move decimal point to the right or 1000 Hecto (h) multiply. units 100 units Deka (da) 10 Basic units Unit Gram (g) Meter (m) Deci (d) Liter (l) 0. 1 Centi (c) units To convert to a larger 0. 01 unit, move decimal point units Milli (m) to the left or divide 0. 001 units

THERE ARE… 1000 millimeters (mm) in a meter (m) 100 centimeters (cm)in a meter (m) 10 decimeters (d) in a meter (m) 1 meter (m) in a meter (m) 10 meters (m) equals 1 dekameters (da) • 100 meters (m) equals 1 hectometer (h) • 1000 meters (m) equals 1 kilometer (k) • • •

MEASURING LENGTHS LONGER THAN A METER EXAMPLE: The distance from point A to point B is 5. 8 m. What is that distance in KILOMETERS?

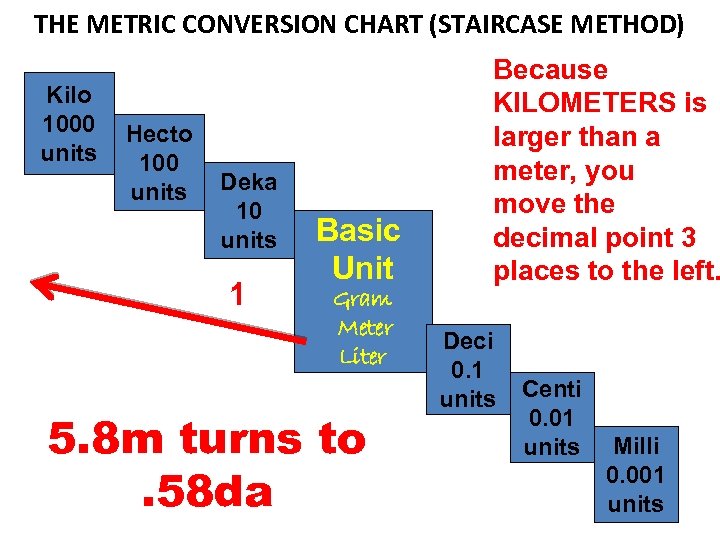THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo 1000 units Hecto 100 units Deka 10 units 1 Basic Unit Gram Meter Liter 5. 8 m turns to. 58 da Because KILOMETERS is larger than a meter, you move the decimal point 3 places to the left. Deci 0. 1 units Centi 0. 01 units Milli 0. 001 units

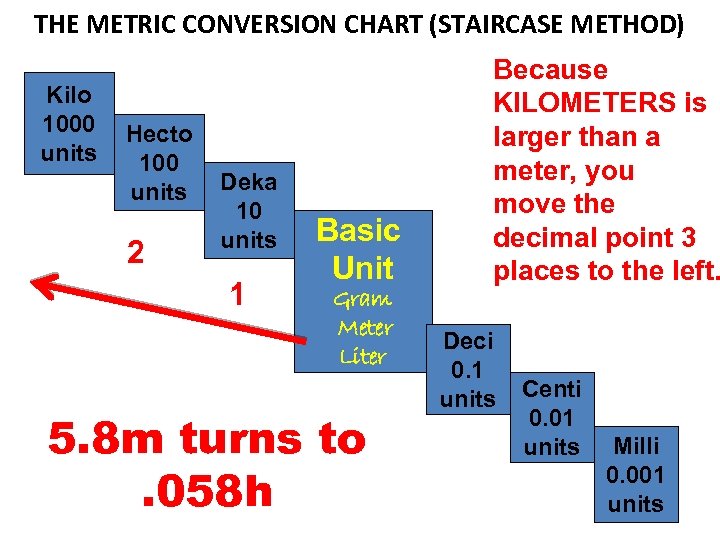THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo 1000 units Hecto 100 units 2 Deka 10 units 1 Basic Unit Gram Meter Liter 5. 8 m turns to. 058 h Because KILOMETERS is larger than a meter, you move the decimal point 3 places to the left. Deci 0. 1 units Centi 0. 01 units Milli 0. 001 units

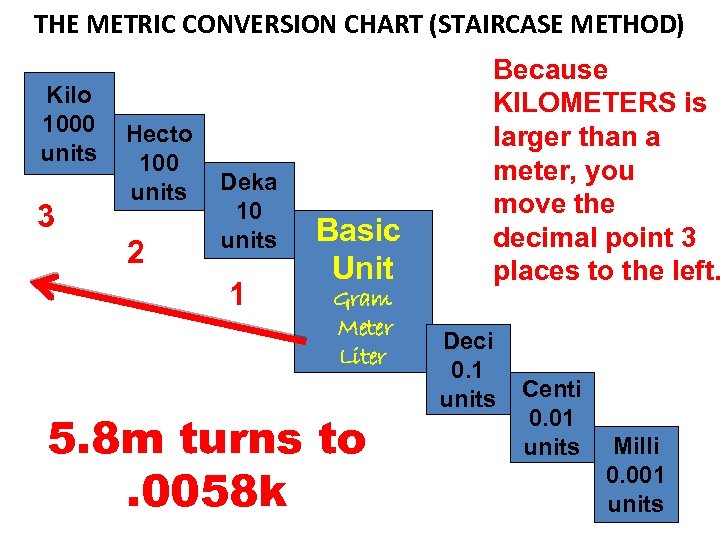THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo 1000 units 3 Hecto 100 units 2 Deka 10 units 1 Basic Unit Gram Meter Liter 5. 8 m turns to. 0058 k Because KILOMETERS is larger than a meter, you move the decimal point 3 places to the left. Deci 0. 1 units Centi 0. 01 units Milli 0. 001 units

MEASURING LENGTHS LONGER THAN A METER EXAMPLE: The distance from point A to point B is 50. 35 k (KILOMETERS). What is that distance in METERS?

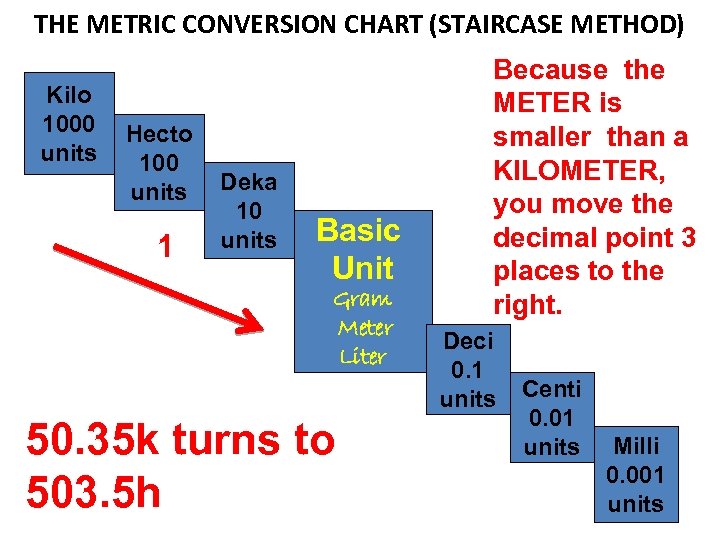THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo 1000 units Hecto 100 units 1 Deka 10 units Basic Unit Gram Meter Liter 50. 35 k turns to 503. 5 h Because the METER is smaller than a KILOMETER, you move the decimal point 3 places to the right. Deci 0. 1 units Centi 0. 01 units Milli 0. 001 units

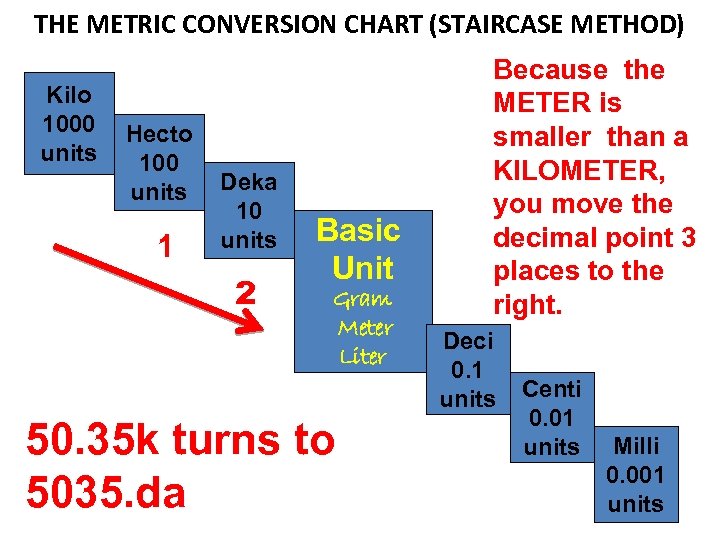THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo 1000 units Hecto 100 units 1 Deka 10 units 2 Basic Unit Gram Meter Liter 50. 35 k turns to 5035. da Because the METER is smaller than a KILOMETER, you move the decimal point 3 places to the right. Deci 0. 1 units Centi 0. 01 units Milli 0. 001 units

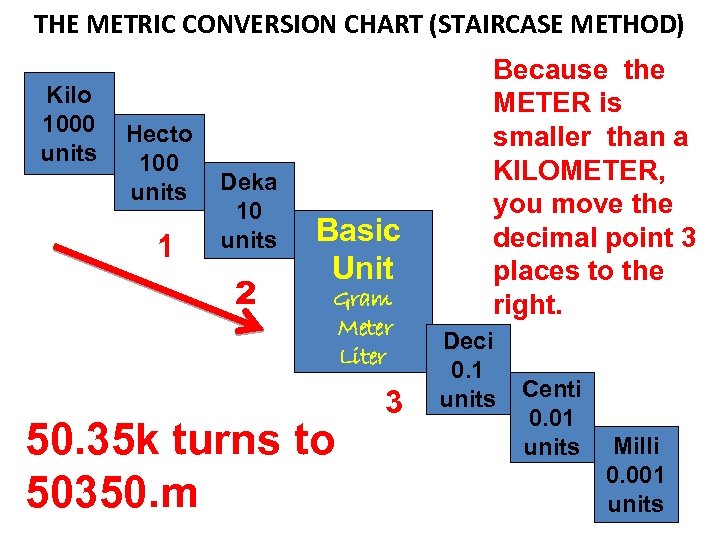THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo 1000 units Hecto 100 units 1 Deka 10 units 2 Basic Unit Gram Meter Liter 50. 35 k turns to 50350. m 3 Because the METER is smaller than a KILOMETER, you move the decimal point 3 places to the right. Deci 0. 1 units Centi 0. 01 units Milli 0. 001 units

MEASURING LENGTHS SMALLER THAN A METER

The two units that measure the length of smaller objects are, … • Decimeter • Centimeter • Millimeter

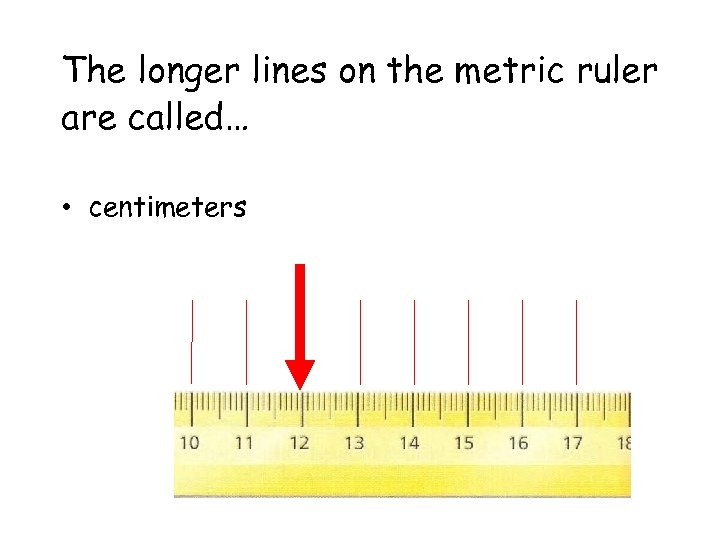The longer lines on the metric ruler are called… • centimeters

The shorter lines on the metric ruler are called… • millimeters

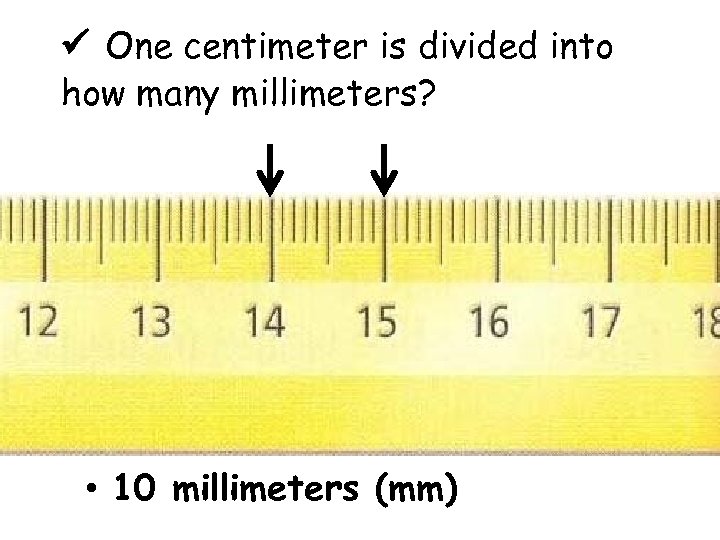One centimeter is divided into how many millimeters? • 10 millimeters (mm)

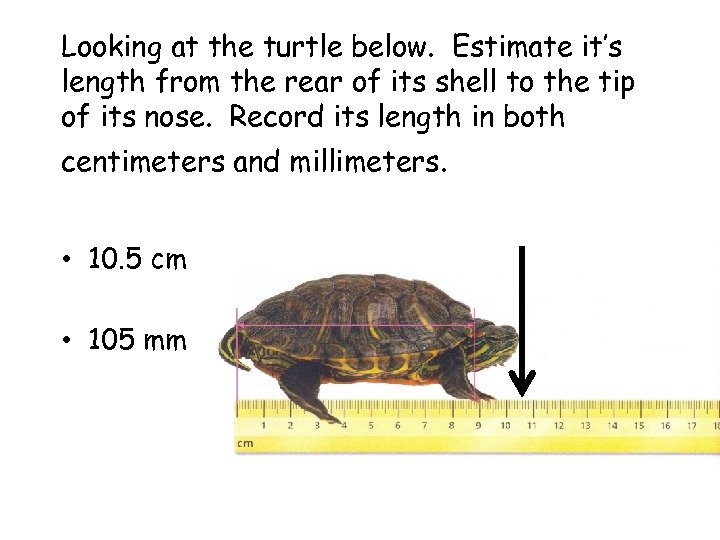Looking at the turtle below. Estimate it’s length from the rear of its shell to the tip of its nose. Record its length in both centimeters and millimeters. • 10. 5 cm • 105 mm

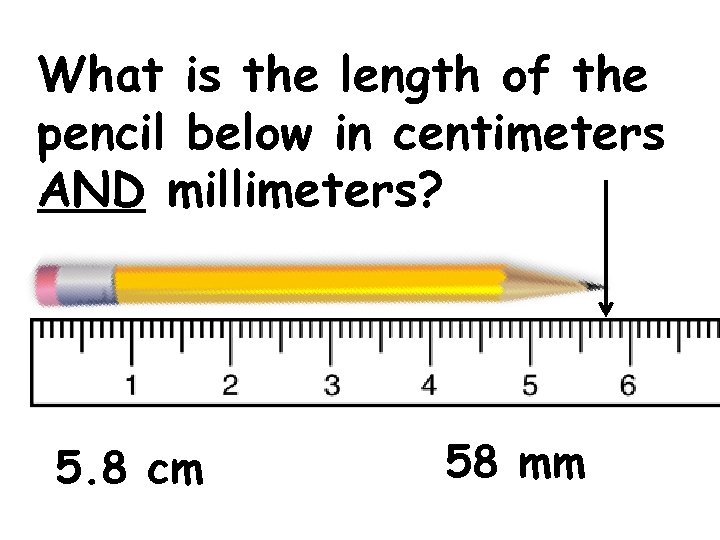What is the length of the pencil below in centimeters AND millimeters? 5. 8 cm 58 mm

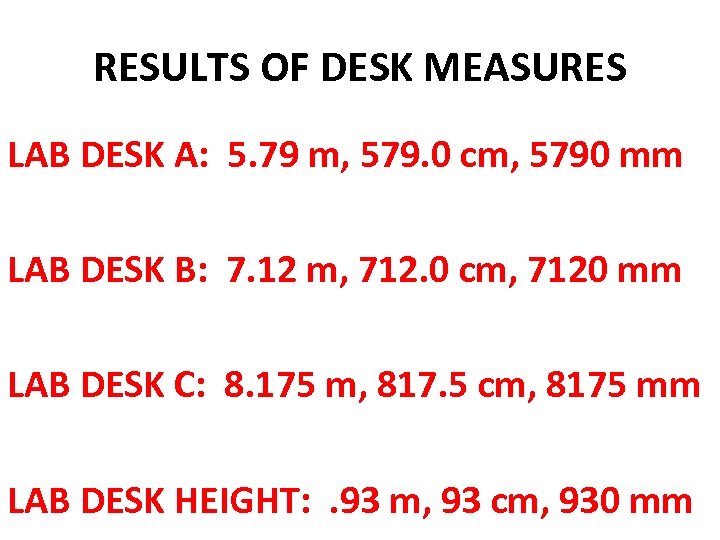RESULTS OF DESK MEASURES LAB DESK A: 5. 79 m, 579. 0 cm, 5790 mm LAB DESK B: 7. 12 m, 712. 0 cm, 7120 mm LAB DESK C: 8. 175 m, 817. 5 cm, 8175 mm LAB DESK HEIGHT: . 93 m, 93 cm, 930 mm

VOLUME

Volume • The amount of space that matter occupies • All matter has volume • Measurement of 3 dimensional objects

The basic unit of measure for VOLUME is the LITER

COMMON UNITS OF VOLUME • Liter (L) • Milliliter (m. L) • Cubic Centimeter (cm³)

THE METRIC CONVERSION CHART (STAIRCASE METHOD) Kilo (k) To convert to a smaller unit, move decimal point to the right or 1000 Hecto (h) multiply. units 100 units Deka (da) 10 Basic units Unit Gram (g) Meter (m) Deci (d) Liter (l) 0. 1 Centi (c) units To convert to a larger 0. 01 unit, move decimal point units Milli (m) to the left or divide 0. 001 units

How many milliliters are in 13 Liters?

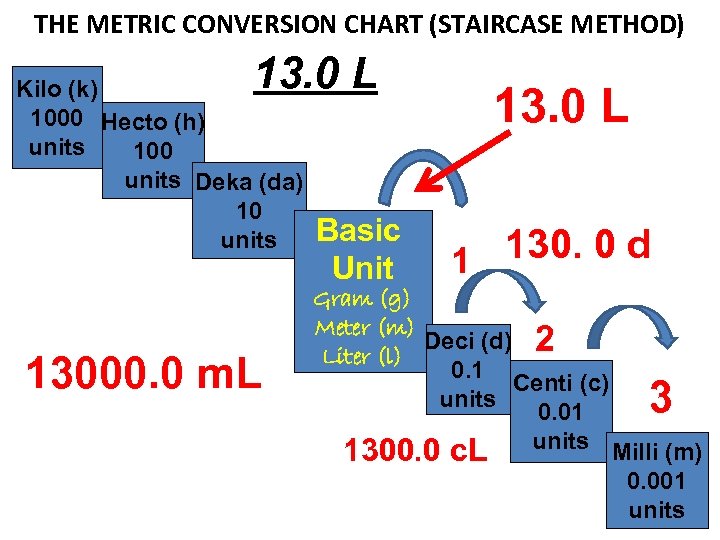THE METRIC CONVERSION CHART (STAIRCASE METHOD) 13. 0 L Kilo (k) 1000 Hecto (h) units 100 units Deka (da) 10 units 13000. 0 m. L Basic Unit 13. 0 L 130. 0 d 1 Gram (g) Meter (m) Deci (d) 2 Liter (l) 0. 1 Centi (c) units 0. 01 1300. 0 c. L units Milli (m) 3 0. 001 units

TOOLS TO MEASURE VOLUME • Metric ruler –Regular shaped objects • Graduated Cylinder –Irregular shaped objects –liquids

EQUATING UNITS OF VOLUME • 1 L = 1, 000 m. L • 1 m. L = 0. 001 L • 1 m. L = 1 cm³

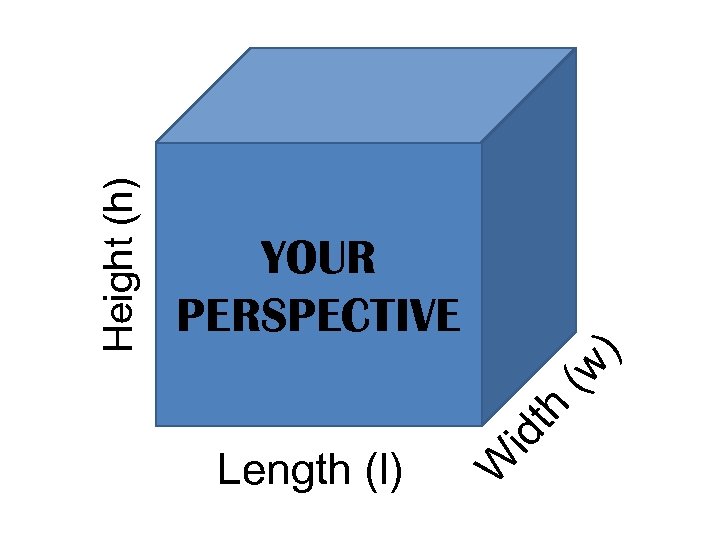
CALCULATING VOLUME • Using a metric ruler Volume = length X width X height of an object

) (w th Length (l) W id Height (h) YOUR PERSPECTIVE

24. 25. 26. 27. 28. 29. METRIC SYSTEM Metric System Notes – Length Metric man Metric Woman Metric Spy Metric Shuttle 2 blank sheets of paper a) Label Measurements in Meters (1) b) Label Graph in Meters (2) 30. VOLUME ACTIVITY 31. 10 sheets of notebook paper

VOLUME ACTIVITY INSTRUCTIONS • Number the paper 1 – 20 • Measure each piece of wood for its VOLUME in centimeters AND millimeters

TODAY IS: Thursday October 30, 2008 • Are your backpacks in your lockers? They are not permitted. • Did you use the restroom before this class? No passes will be issued. • Did you bring all your materials to class? A requirement • Is your folder available? A requirement

What tool is used to measure the VOLUME of irregular shaped objects?

The GRADUATED CYLINDER

LIQUIDS AND IRREGULAR SHAPED OBJECTS ARE MEASURED IN LITERS THERE ARE 1000 MILILITER IN A LITER

Graduated Cylinders come in a variety of sizes: • 10 ml • 25 ml • 50 ml • 100 ml • 500 ml • 1000 ml

How do you read a GRADUADTED CYLINDER?

Know the GRADUATES and the SUBGRADUATES 20 SUBGRADUATES 10

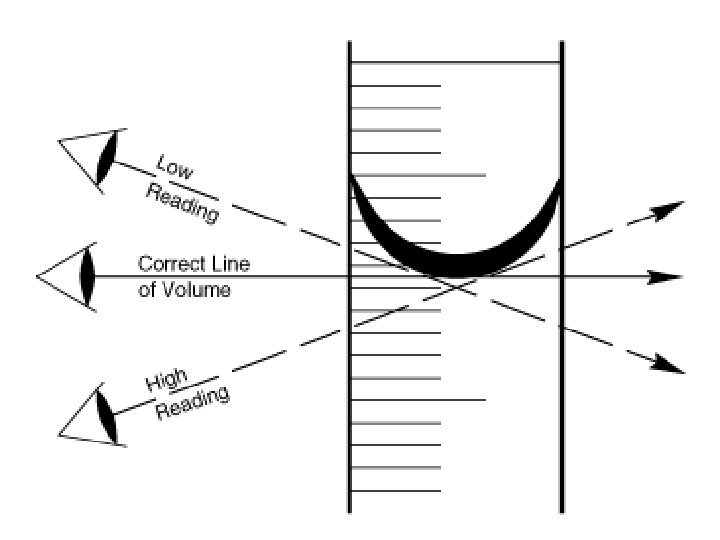
Note the MENISCUS • The meniscus is the area where the fluid molecules are more attracted to the glass material than itself.

The measurement is at the bottom of the convex or meniscus. Reading is 18 m. L NOT 18. 5 m. L

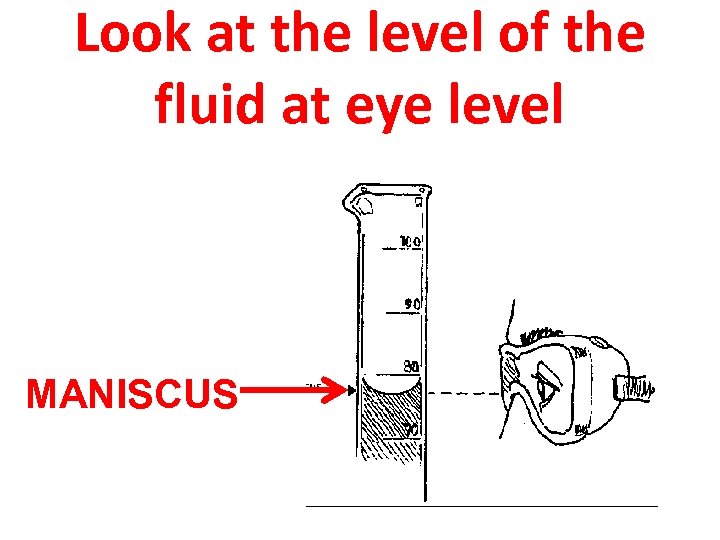Look at the level of the fluid at eye level MANISCUS

X

What is the VOLUME of this liquid? 6. 6 m. L

What is the VOLUME of this liquid? 11. 5 m. L

What is the VOLUME of this liquid? 53. 0 m. L

What is the VOLUME of this liquid? 76. 0 m. L

What is the VOLUME of this liquid? 293. 0 m. L

• Using a GRADUATED CYLINDER –Item is dropped into a predetermined amount of water in the cylinder. –The item places the cylinder –The item will displace the same amount of water as its matter. –The difference between the original volume of water and the level of the water with the object is its volume.

MATERIALS • Graduated Cylinder • Pipette (used to add or take out a fluid from the cylinder) • Beaker (small) (used with the pipette) • 4. 5 cm bolt • 7 cm bolt • 11 cm bolt • Ruler (to measure the bolts)

INSTRUCTIONS • Make a table as seen below: BOLT BEGINNING LEVEL (m. L) ENDING LEVEL (m. L) VOLUME (m. L) 4. 5 cm 7. 0 cm 9. 5 cm Determine the VOLUME of each item

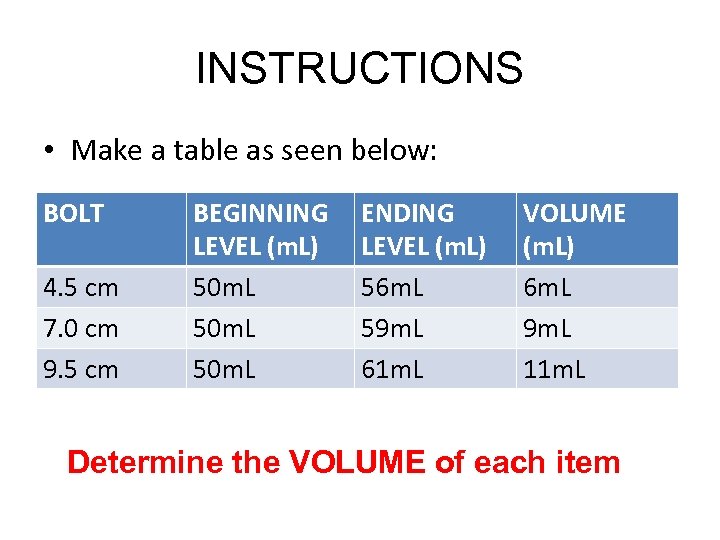INSTRUCTIONS • Make a table as seen below: BOLT 4. 5 cm 7. 0 cm 9. 5 cm BEGINNING LEVEL (m. L) 50 m. L ENDING LEVEL (m. L) 56 m. L 59 m. L 61 m. L VOLUME (m. L) 6 m. L 9 m. L 11 m. L Determine the VOLUME of each item

WEIGHT vs. MASS

WEIGHT • A measurement of the force of gravity on an object. • Weight can change with a location. –On the moon a 120 pound person can weigh 20 pounds. –You will weigh less the further away from the center of the earth.

MASS • The amount of matter in an object • Mass does not change with location. • Scientists prefer to measure the mass of an object than its weight because weight changes with location.

The basic unit of weight and mass is the GRAM (g)

What tool is used to measure the MASS of an object?

Triple Beam Balance

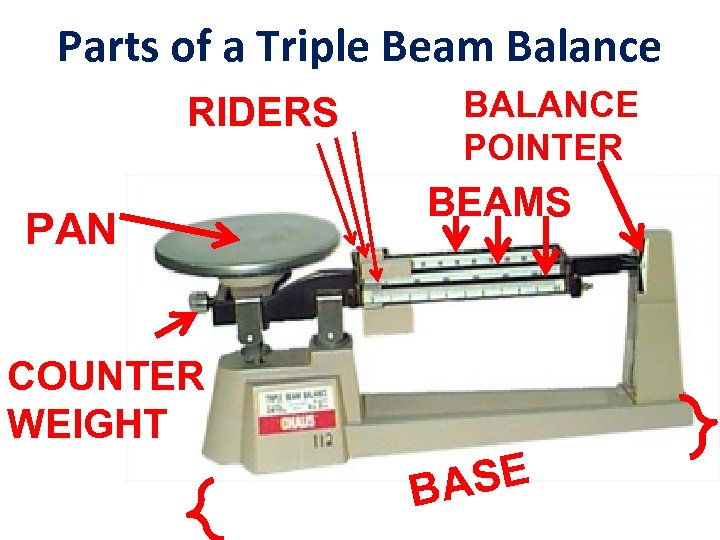Parts of a Triple Beam Balance RIDERS PAN BALANCE POINTER BEAMS COUNTER WEIGHT SE BA

Instructions on use With the pan empty, move three riders on the three beams to their leftmost positions, so that the balance reads zero.

If the indicator on the far right is not aligned with the fixed mark, then calibrate the balance by turning the set screw on the left under the pan.

Once the balance has been calibrated, place the object to be measured on the pan.

Move the 100 gram rider along the beam to the right until the indicator drops below the fixed mark. The notched position immediately to the left of this point indicates the number of hundreds of grams.

Now move the 10 gram rider along the beam to the right until the indicator drops below the fixed mark. The notched position immediately to the left of this point indicates the number of tens of grams.

The beam in front is notched; the rider can move anywhere along the beam. The boldface numbers on this beam are grams and the tick marks between the boldface numbers indicate tenths of grams.

To find the mass of the object on the pan, simple add the numbers from the three beams.

INSTRUCTIONS • Make a table as seen below: BOLT MASS (g) 4. 5 cm 7. 0 cm 9. 5 cm Determine the MASS of each item

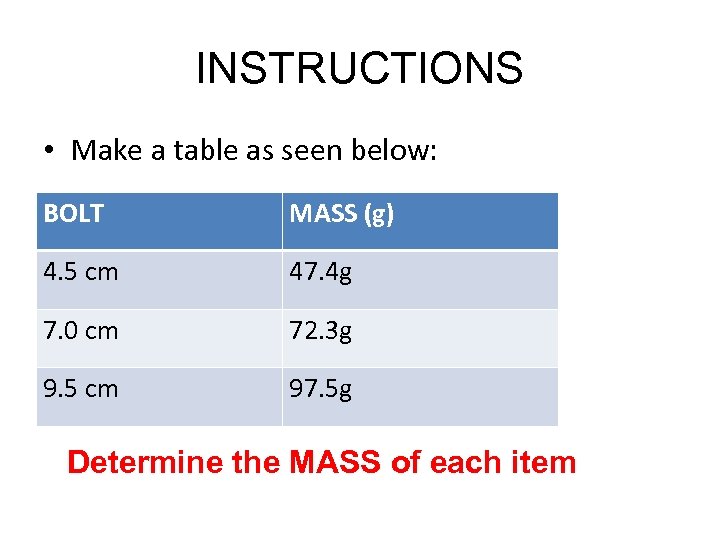INSTRUCTIONS • Make a table as seen below: BOLT MASS (g) 4. 5 cm 47. 4 g 7. 0 cm 72. 3 g 9. 5 cm 97. 5 g Determine the MASS of each item

DENSITY • Many objects have the same volume but have different masses. • Density relates to the amount of matter in a given volume. • Expressed as the number of grams in a cubic centimeter • Formula is DENSITY = MASS ÷ VOLUME

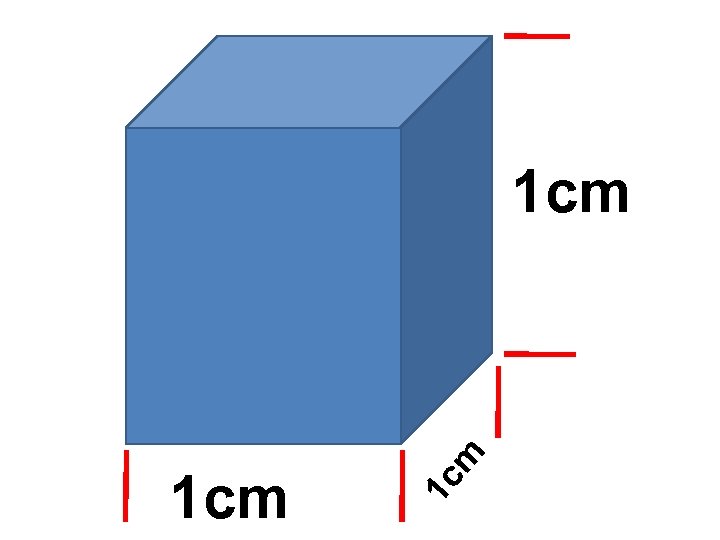1 c 1 cm m 1 cm

WHY DO SOME OBJECTS FLOAT WHILE OTHERS SINK?

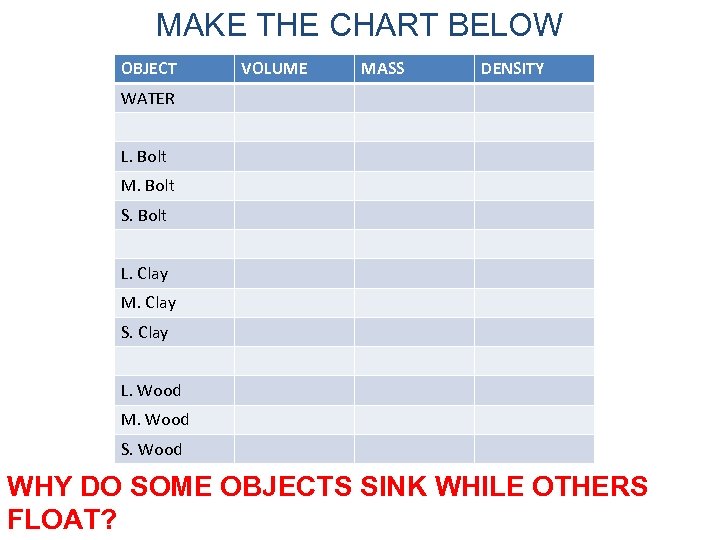MAKE THE CHART BELOW OBJECT VOLUME MASS DENSITY WATER L. Bolt M. Bolt S. Bolt L. Clay M. Clay S. Clay L. Wood M. Wood S. Wood WHY DO SOME OBJECTS SINK WHILE OTHERS FLOAT?

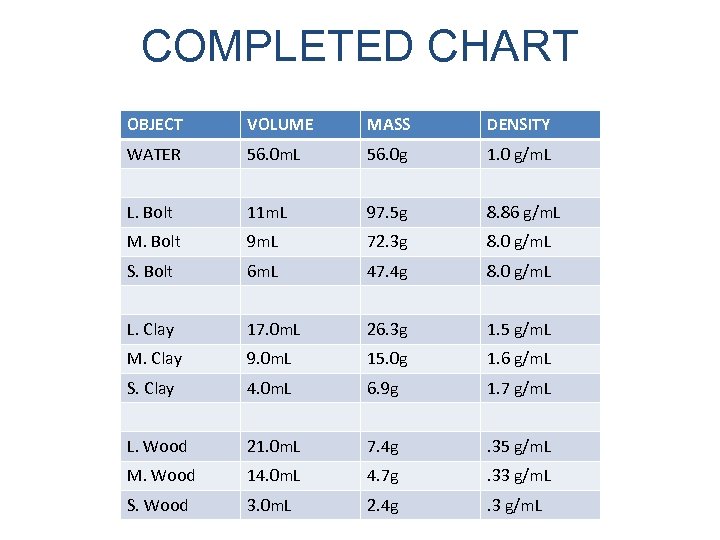COMPLETED CHART OBJECT VOLUME MASS DENSITY WATER 56. 0 m. L 56. 0 g 1. 0 g/m. L L. Bolt 11 m. L 97. 5 g 8. 86 g/m. L M. Bolt 9 m. L 72. 3 g 8. 0 g/m. L S. Bolt 6 m. L 47. 4 g 8. 0 g/m. L L. Clay 17. 0 m. L 26. 3 g 1. 5 g/m. L M. Clay 9. 0 m. L 15. 0 g 1. 6 g/m. L S. Clay 4. 0 m. L 6. 9 g 1. 7 g/m. L L. Wood 21. 0 m. L 7. 4 g . 35 g/m. L M. Wood 14. 0 m. L 4. 7 g . 33 g/m. L S. Wood 3. 0 m. L 2. 4 g . 3 g/m. L

BASED ON YOUR DATA WHY DO SOME OBJECTS FLOAT WHILE OTHERS SINK?

OBJECTS WITH A DENSITY LESS THAN ONE WILL SINK IN WATER

If 5. 6 m. L of water has a mass of 5. 6 g, what would be its DENSITY? 1 g/m. L

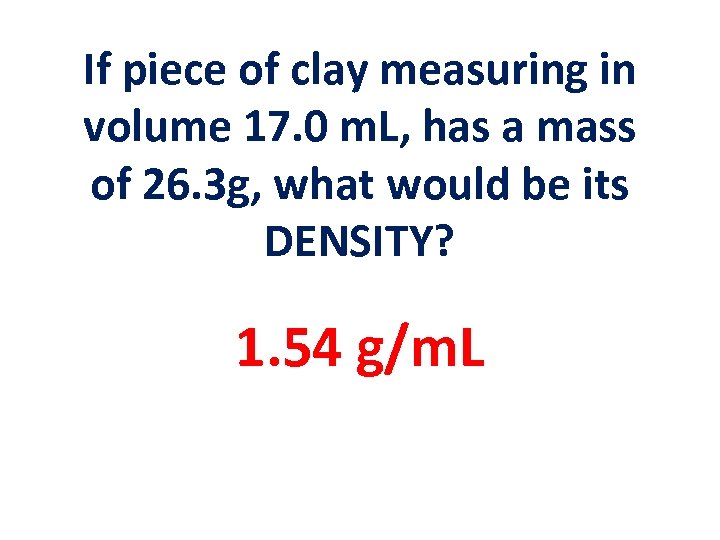If piece of clay measuring in volume 17. 0 m. L, has a mass of 26. 3 g, what would be its DENSITY? 1. 54 g/m. L

If piece of 21. 0 m. L piece of wood had a mass of 7. 4 g, what would be its DENSITY? . 35 g/m. L

If a 97. 5 g piece of metal had a volume of 11. 0 m. L, what would be its DENSITY? 8. 86 g/m. L

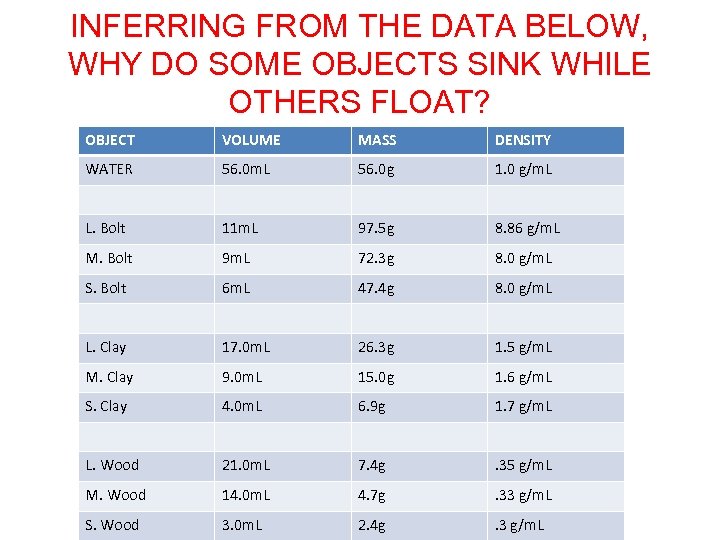INFERRING FROM THE DATA BELOW, WHY DO SOME OBJECTS SINK WHILE OTHERS FLOAT? OBJECT VOLUME MASS DENSITY WATER 56. 0 m. L 56. 0 g 1. 0 g/m. L L. Bolt 11 m. L 97. 5 g 8. 86 g/m. L M. Bolt 9 m. L 72. 3 g 8. 0 g/m. L S. Bolt 6 m. L 47. 4 g 8. 0 g/m. L L. Clay 17. 0 m. L 26. 3 g 1. 5 g/m. L M. Clay 9. 0 m. L 15. 0 g 1. 6 g/m. L S. Clay 4. 0 m. L 6. 9 g 1. 7 g/m. L L. Wood 21. 0 m. L 7. 4 g . 35 g/m. L M. Wood 14. 0 m. L 4. 7 g . 33 g/m. L S. Wood 3. 0 m. L 2. 4 g . 3 g/m. L

OBJECTS WITH A DENSITY LESS THAN ONE WILL SINK IN WATER

TODAY IS THURSDAY November 6, 2008 • Get out your notebooks and be prepared to take quick notes. • We will be starting the lab as soon as everyone is ready.

ON THE NEXT BLANK PAGE OF YOUR FOLDER…. • NUMBER 1 - 15 on the left • NUMBER 16 – 30 in the middle • NUMBER 31 – 50 on the right • DO NOT SKIP LINES

WHAT IS TEMPERATURE? A measure of the average kinetic energy of the individual particles of matter

What tool do you use to measure TEMERATURE?

THERMOMETER

HOW DOES A THERMOMETER WORK? • Temperature is measured with a thermometer usually made of a glass tube with colored alcohol. • Certain materials have EXPANSION properties or they stretch when heated and shrink when cooled. • As the air gets hotter, the level of the liquid rises and, as the air gets cooler, the level falls.

How do you read a THERMOMETER? • Know the scale in which thermometer is registering. (F, C, K) • Look at thermometer at eye level to get the correct reading.

What are the different scales used to measure TEMERATURE?

Fahrenheit (F°) • Most common scale used in the United States • Freezing is 32°F • Boiling is 212°F

Celsius (°C) • Most common scale used in other countries • Freezing point is 0°C • Boiling point is 100°C

Kelvin (K) • Most commonly used in physical science • A Kelvin degree is the same size as a Celsius • Water freezes at 273 K • Water boils at 373 K • No more thermal energy can be removed at -273 K • -273 K is called absolute zero

Fahrenheit to Celsius Conversion Celsius= 5/9 X (Fahrenheit-32) EXAMPLE: Convert 106°Fahrenheit into Celsius =5/9 X (Fahrenheit -32) Celsius = 5/9 X 74 Celsius = 41. 11°

PRACTICE Convert 72° Fahrenheit into Celsius =5/9 X (Fahrenheit -32) Celsius = 5/9 X (72°F- 32°F) Celsius = 5/9 X 42°F Celsius = 23. 33 C°

PRACTICE Convert 168° Fahrenheit into Celsius =5/9 X (Fahrenheit -32) Celsius = 5/9 X (168°F – 32°F) Celsius = 5/9 X 136°F Celsius = 75. 5 C°

Celsius to Fahrenheit Conversion Fahrenheit= (9/5 X Celsius) +32 EXAMPLE: Convert 41. 11°C into Fahrenheit = (9/5 X 41. 1°C) + 32°F Fahrenheit = 73. 98°C + 32°F Fahrenheit = 106°F

PRACTICE Fahrenheit= (9/5 X Celsius) +32 EXAMPLE: Convert 72°C into Fahrenheit = (9/5 X 72°C) + 32°F Fahrenheit = 129. 6°C + 32°F Fahrenheit = 161. 6 F°

PRACTICE Fahrenheit= (9/5 X Celsius) +32 EXAMPLE: Convert 127°C into Fahrenheit = (9/5 X 127°C) + 32°F Fahrenheit = 228. 6°C + 32°F Fahrenheit = 260. 6 F°