ME 451 Kinematics and Dynamics of Machine Systems

ME 451 Kinematics and Dynamics of Machine Systems Review of Linear Algebra 2. 1 through 2. 4 Th, Jan. 22 © Dan Negrut, 2009 ME 451, UW-Madison

Before we get started… l Last time: l l Syllabus Quick overview of course Starting discussion about vectors, their geometric representation HW Assigned: l l l ADAMS assignment, will be emailed to you today Problems: 2. 1. 2, 2. 1. 3 Due in one week 2

Basis (Unit Coordinate) Vectors l Basis (Unit Coordinate) Vectors: a set of unit vectors used to express all other vectors l In this class, to simplify our life, we use a set of two orthogonal unit vectors l A vector a can then be resolved into components x and y l Nomenclature: l Notation convention: throughout this class, vectors/matrices are in bold font, scalars are not (most often they are in italics) and , along the axes are called the Cartesian components of the vector 3

Geometric Vectors: Operations l Regarding the angle between two vectors, note that l l Dot product of two vectors, definition: l l The dot-product of two vectors is commutative Since the angle between coordinate unit vectors is /2: l 4 Important: Angles are positive counterclockwise Therefore, the projection ax and ay on the two axes are

Geometric Vectors: Operations l The distributive property of the dot product (take it at face value) l If you buy the relation above (and you should), the following holds: l Given a vector , the orthogonal vector is obtained as 5

Geometric Vectors: Moving away… l Geometric vectors, concluding remarks: l l l Easy to visualize, but cumbersome to work with The major drawback: hard to manipulate, especially when it comes to computers, which are good at storing matrices and vectors… …and this motivates the algebraic representation of a vector, which is now married to a Reference Frame l Reference Frame (RF): as soon as you define the coordinate unit vectors and , you defined a RF l We’re going to exclusively work with right hand mutually orthogonal RFs 6

Algebraic representation of vectors l It all hinges upon the following representation: l Then we can write this: l In the algebraic notation, drop the arrow… 7

What can you do with algebraic vectors? l Everything that you could with the geometric vectors l This is just a different notation (representation) of the same concept l Scale them l Add them (this is very simple now) l Multiply two of them l l Inner product (leads to a number) Measure the angle between two of them 8

Algebraic Vector and Reference Frames l Recall that an algebraic vector is just a representation of a geometric vector in a particular reference frame (RF) l Question: What if I now want to represent the same geometric vector in a different RF? 9

Algebraic Vector and Reference Frames l Representing the same geometric vector in a different RF leads to the concept of Rotation Matrix A: l Getting the new coordinates, that is, representation of the same geometric vector in the new RF is as simple as multiplying the coordinates by the rotation matrix A: l NOTE 1: what is changed is the RF used for representing the vector, and not the underlying geometric vector l NOTE 2: rotation matrix A is sometimes called “orientation matrix” 10

The Rotation Matrix A l Very important observation: the matrix A is orthogonal: 11

Important Relation l Expressing a given vector in one reference frame (local) in a different reference frame (global) Also called a change of base. 12

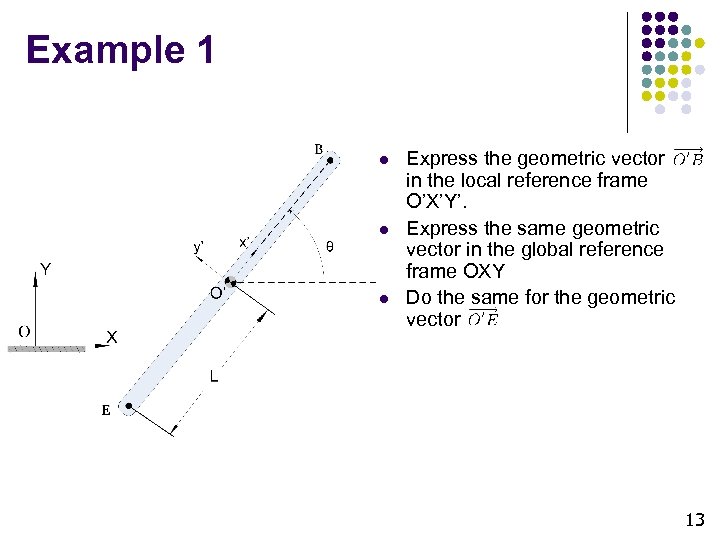Example 1 l l l Express the geometric vector in the local reference frame O’X’Y’. Express the same geometric vector in the global reference frame OXY Do the same for the geometric vector 13

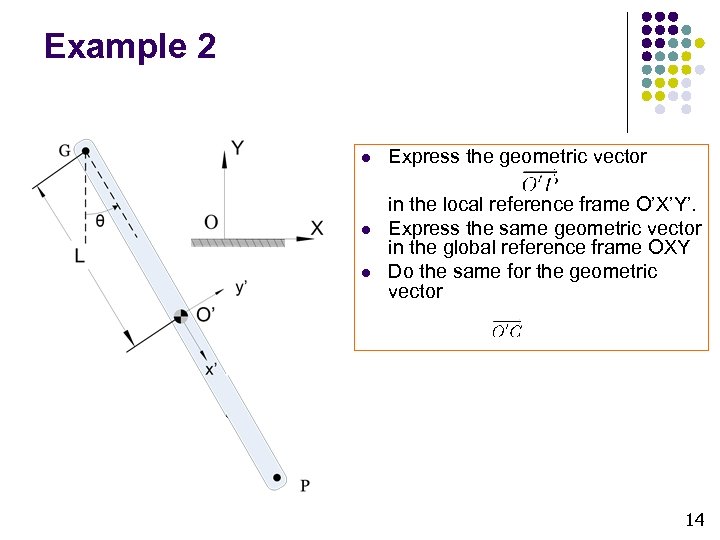Example 2 l l l Express the geometric vector in the local reference frame O’X’Y’. Express the same geometric vector in the global reference frame OXY Do the same for the geometric vector 14

Translation + Rotation l What we just discussed dealt with the case when you are interested in finding the representing the location of a point P when you change the reference frame, but yet the new and old reference frames share the same origin l What if they don’t share the same origin? How would you represent the position of the point P in this new reference frame? 15

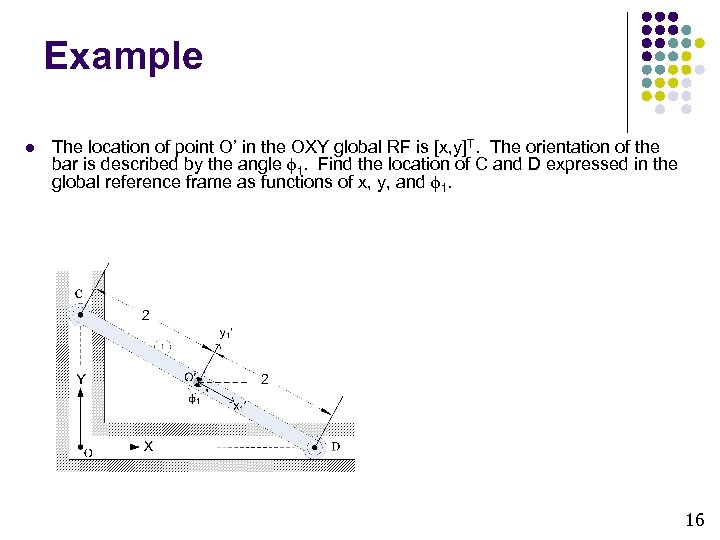Example l The location of point O’ in the OXY global RF is [x, y]T. The orientation of the bar is described by the angle 1. Find the location of C and D expressed in the global reference frame as functions of x, y, and 1. 16

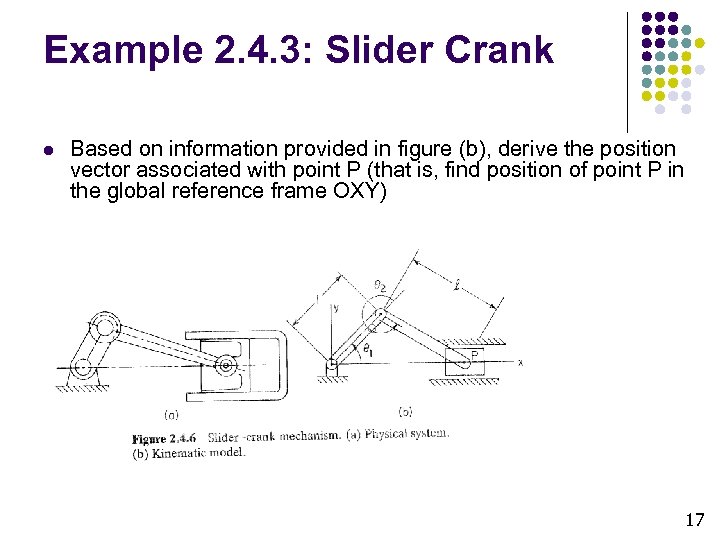Example 2. 4. 3: Slider Crank l Based on information provided in figure (b), derive the position vector associated with point P (that is, find position of point P in the global reference frame OXY) O 17

Example (RGC) l Use the array q of generalized coordinates to locate the point B in the GRF 18