МБОУ лицей № 3 «Формула Пика и её приложения» Выполнил: Крыжевич Павел, ученик 10 «А» класса Руководитель: Чашурина Н. А. , учитель математики г. Сургут, 2011 г.

Введение В результате проведённого мной опроса, из 50 опрошенных только 2 знают о формуле Пика и её применении в алгебре и геометрии. Поэтому я считаю нужным рассказать о такой полезной формуле, позволяющей вычислять площадь плоской фигуры, лежащей на сетке.

Актуальность данного проекта состоит в том, что вычисление площади является одним из заданий в Едином Государственном Экзамене (задание B 6). Существует множество способов вычислить площадь фигуры, но по моему мнению формула Пика является наиболее удобным.

Цель проекта Перед собой я поставил одну цель: показать новый способ вычисления площади фигуры с помощью формулы Пика. Объект исследования: формула Пика. Предмет исследования: применение формулы Пика.

Задачи проекта Изучить литературу по данной теме; Провести опрос учащихся для создания примерной картины осведомленности о данном методе вычисления площади; Узнать все преимущества и недостатки формулы Пика; Привести примеры использования (приложения) формулы.

Многоугольники на решётке Линии, идущие по сторонам клеток, образуют решётку, а вершины клеток – узлы этой решётки. Если нарисовать на листе многоугольник с вершинами в узлах, то можно найти его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить.
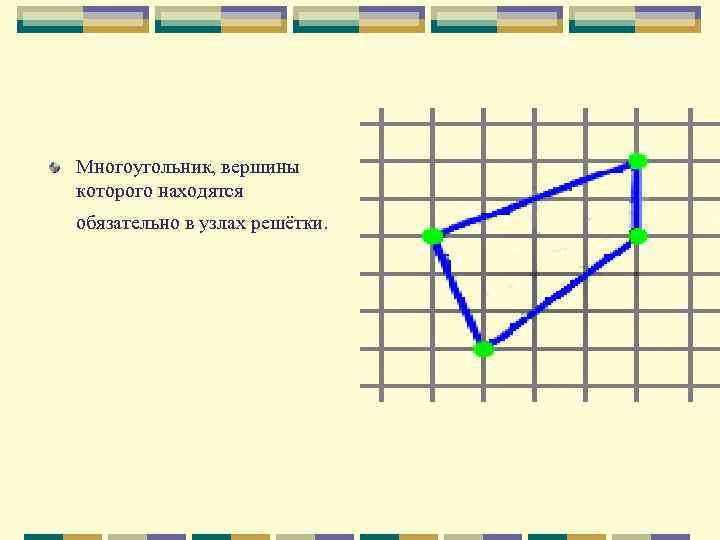
Многоугольник, вершины которого находятся обязательно в узлах решётки.
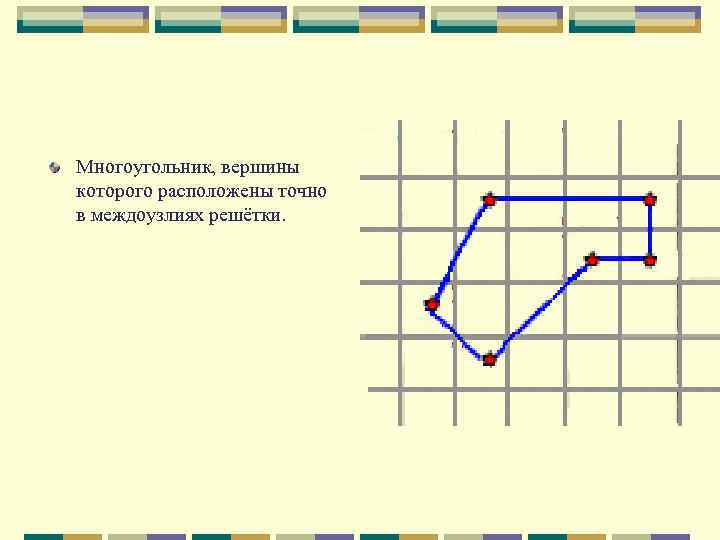
Многоугольник, вершины которого расположены точно в междоузлиях решётки.

Формула Пика , где: S - площадь многоугольника; В - количество узлов сетки, лежащих внутри многоугольника; Г - количество узлов сетки, лежащих на границе многоугольника.

Преимущества формулы Пика Для нахождения площади фигуры не нужно представлять другую фигуру, сложенную из частей данной (это не всегда возможно); Не требуется сложных математических вычислений; Для заполнения формулы все данные есть на рисунке (не требуется дополнительных построений). Главными плюсами формулы Пика я считаю легкость в использовании и преимущество во времени в отличие от стандартных способов вычисления площади.

Дан произвольный треугольник ABC. Вычислите его площадь. Стандартный способ: SABC=Sпр-Sк. т. -Sз. т. Sпр =3× 10=30; Sк. т. =(3× 1): 2=1, 5; Sз. т. =(3× 10): 2=15. SABC=30 -1, 5 -15=13, 5 По формуле Пика: В=9; Г=11 S=9+11: 2 -1=13, 5
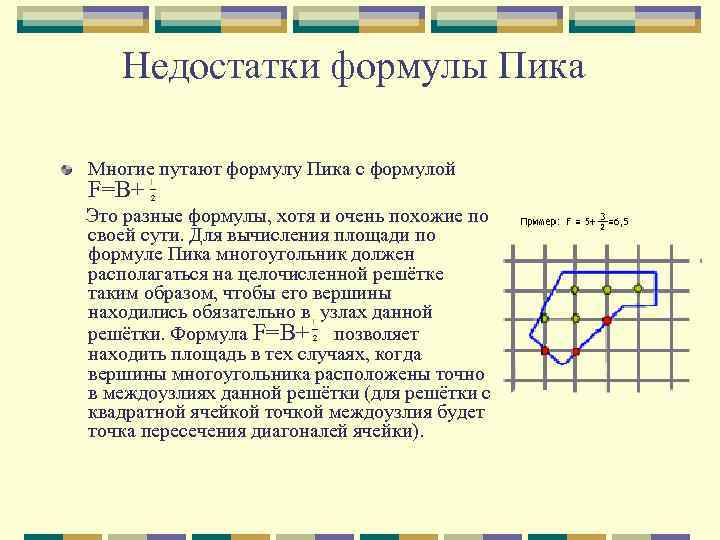
Недостатки формулы Пика Многие путают формулу Пика с формулой F=В+ Это разные формулы, хотя и очень похожие по своей сути. Для вычисления площади по формуле Пика многоугольник должен располагаться на целочисленной решётке таким образом, чтобы его вершины находились обязательно в узлах данной решётки. Формула F=В+ позволяет находить площадь в тех случаях, когда вершины многоугольника расположены точно в междоузлиях данной решётки (для решётки с квадратной ячейкой точкой междоузлия будет точка пересечения диагоналей ячейки).
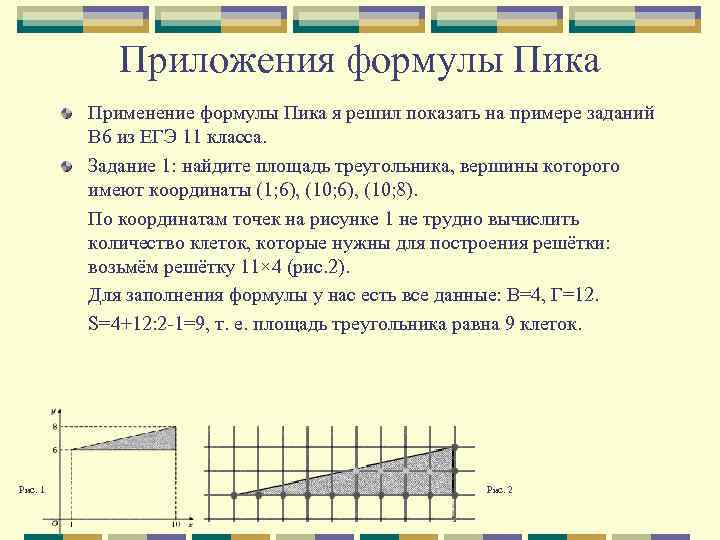
Приложения формулы Пика Применение формулы Пика я решил показать на примере заданий B 6 из ЕГЭ 11 класса. Задание 1: найдите площадь треугольника, вершины которого имеют координаты (1; 6), (10; 8). По координатам точек на рисунке 1 не трудно вычислить количество клеток, которые нужны для построения решётки: возьмём решётку 11× 4 (рис. 2). Для заполнения формулы у нас есть все данные: В=4, Г=12. S=4+12: 2 -1=9, т. е. площадь треугольника равна 9 клеток. Рис. 1 Рис. 2

Задание 2: найдите площадь квадрата (рис. 1), вершины которого имеют координаты (8; 0), (10; 8), (2; 10), (0; 2). Так же, как и в 1 задании, задаём размеры решётки: 12× 12 (рис. 2). Заполняем формулу: S=65+8: 2 -1=68, т. е. площадь равна 68 клеткам. рис. 1 рис. 2

Здесь некоторые примеры задач, в которых можно воспользоваться формулой Пика: 1. Шахматный король обошел доску 8× 8 клеток, побывав на каждом поле ровно один раз и последним ходом вернувшись на исходное поле. Ломаная, соединяющая последовательно центры полей, которые проходил король, не имеет самопересечений. Какую площадь может ограничивать эта ломаная? 2. Вычислить площадь указанного параллелограмма (как функцию от [ABCD]), если стороны параллелограмма ABCD разделены на n и m равных частей. 3. Середины сторон квадрата соединены отрезками с вершинами. Найти отношение площади квадрата к площади восьмиугольника, образованного проведенными отрезками.

Задача: Середины сторон квадрата соединены отрезками с вершинами так, как это показано на рисунке 1. Найти отношение площади квадрата к площади восьмиугольника, образованного проведенными отрезками. Довольно стандартная и распространенная ошибка при решении этой задачи состоит в предположении, что «из симметричности ситуации следует, что восьмиугольник правильный» . Однако это не так: он равносторонний, но углы у него не равны. Так как нам нужно найти отношение площадей, то размеры квадрата для нас роли не играют. Поэтому рассмотрим квадрат, расположенный на целочисленной решетке, размером 12× 12; стороны квадрата лежат на прямых решетки. Тогда, как нетрудно заметить, все вершины восьмиугольника являются узлами решетки; более того, отсюда легко заметить, что этот восьмиугольник правильным не является (рис. 2)— он равносторонний, но не равноугольный. Из формулы Пика теперь легко следует, что площадь восьмиугольника равна 21 + 8/2 − 1 = 24. Поэтому искомое отношение площадей равно 6. Рис. 1 Рис. 2

Вывод В моём выступлении я постарался показать преимущества применения формулы Пика для решения задания B 6 из ЕГЭ 11 класса и нахождения площади многоугольника, помещённого на решётку, вершины которого находятся в её узлах. Я считаю, что необходимо знакомить учащихся 11 классов с данной формулой на уроках алгебры или геометрии, или при подготовке к ЕГЭ.

Литература 1. 2. 1. Книги, энциклопедии: Самое полное издание типовых вариантов заданий ЕГЭ : 2011 : Математика / авт. -сост. И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров и др. : АСТ: Астрель, 2011. – 95, [1] с. – (Федеральный институт педагогических измерений); Рiсk G. Mathematische Annalen. — 1016. — Bd 77. — S. 1— 6. Интернет-ресурсы: 1 сентября