МБОУ классическая гимназия 1 им В Г

Зарегистрируйтесь, чтобы просмотреть полный документ!

МБОУ классическая гимназия № 1 им. В. Г. Белинского Творческая работа по геометрии на тему: «Измерение расстояния до недоступной точки» Выполнила: ученица 9 класса «а» Гарькина Мария Пенза 2012

Геометрическое объяснение «способа козырька» . Этот способ часто применяется военными и туристами. Решение: Луч зрения, касающийся обреза козырька (ладони, записной книжки), первоначально направлен на линию противоположного берега. Когда человек поворачивается, то луч зрения, подобно ножке циркуля, как бы описывает окружность, и тогда расстояние до предмета на том берегу равно расстоянию до предмета на этом берегу.

Измерение расстояния до недоступной точки ( измерение ширины реки). Случай 1: Измерение расстояния между точками Аи В, разделёнными препятствием (рекой). 1)Выберем на берегу реки две доступные точки А и В, расстояние между которыми может быть измерено. 2)Из точки А видны и точка В и точка С, взятая на противоположном берегу. 3)Измерим расстояние АВ, с помощью астролябии измеряем углы А и В, угол АСВ = 1800 - угол А - угол В 4)Зная одну сторону треугольника и все углы, по теореме синусов находим искомое расстояние.

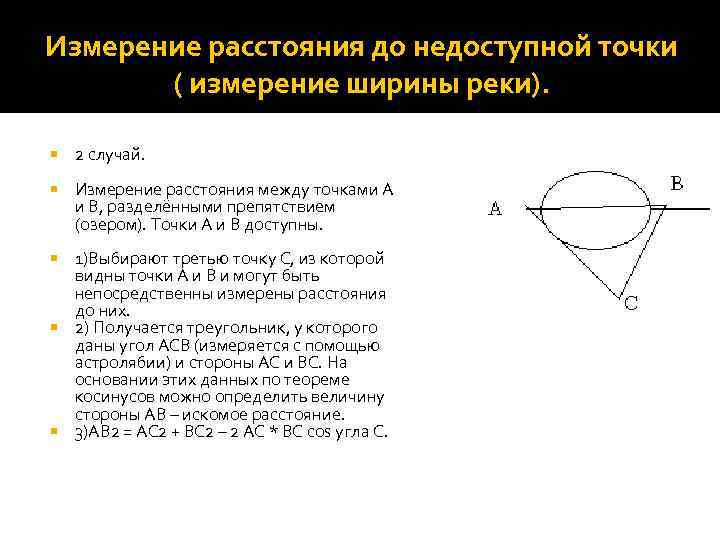
Измерение расстояния до недоступной точки ( измерение ширины реки). 2 случай. Измерение расстояния между точками А и В, разделёнными препятствием (озером). Точки А и В доступны. 1)Выбирают третью точку С, из которой видны точки А и В и могут быть непосредственны измерены расстояния до них. 2) Получается треугольник, у которого даны угол АСВ (измеряется с помощью астролябии) и стороны АС и ВС. На основании этих данных по теореме косинусов можно определить величину стороны АВ – искомое расстояние. 3)АВ 2 = АС 2 + ВС 2 – 2 АС * ВС cos угла С.

Измерение расстояния до недоступной точки ( измерение ширины реки). 3 случай: Измерение расстояния между точками А и В, разделёнными препятствием (лесом) и недоступными определяющему расстояние (точки находятся по ту сторону реки). Выбирают две доступные точки С и К, расстояние между которыми может быть измерено и из которых видны как точка А, так т точка В. 1)Устанавливают астролябию в точке С и измеряют углы АСК и ВСК. 2)Затем измеряют расстояние СК и переносят астролябию в т. К, из которой измеряют углы АКС и АКВ. 3) На бумаге по стороне СК, взятой в определённом масштабе и двум прилежащим углам строят треугольники АСК и ВСК и вычисляют элементы этих треугольников. 4)Проведя на чертеже линию АВ, определяют длину её непосредственно по чертежу или путём вычисления (решают треугольники АВС и АВК, в которые входит определяемая линия АВ).

Геометрическое объяснение способа «зеркала» Своеобразный способ определения высоты дерева - при помощи зеркала. На некотором расстоянии от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку Д, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ЕД), во сколько раз расстояние ВС от зеркала до дерева больше расстояния СД от зеркала до наблюдателя. Почему? Решение: Способ основан на законе отражения света. 1) Вершина А отражается в точке А' так, что АВ=А'В. Из подобия же треугольников ВСА' и СЕД следует, что АВ': ЕД=ВС: СД. 2)В этой пропорции остается лишь заменить А'В равным ему АВ, чтобы обосновать указанное в задаче соотношение. Этот удобный и нехлопотливый способ можно применять во всякую погоду, но не в густом насаждении, а к одиноко стоящему дереву.

Геометрическое объяснение способа Жюля Верна. «-Сегодня нам надо измерить высоту площадки Далекого Вида, - сказал инженер. -Вам понадобится для этого инструмент? - спросил Герберт. - Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. -Тебе знакомы зачатки геометрии? - спросил он Герберта, поднимаясь с земли. -Да. -Помнишь свойства подобных треугольников? - Их сходственные стороны пропорциональны. -Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч. У другого основания треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мой луч зрения, совпадающий с направлением гипотенузы первого треугольника. -Понял! - воскликнул юноша - Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. -Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты» Отрывок из книги Жюля Верна. Оба горизонтальных расстояния были измерены: меньшее - 15 футов, большее - 500 футов. По окончании измерений инженер составил следующую запись: 15: 500=10: х, 500∙ 10=5000, 5000: 15=333, 3 Значит, высота гранитной стены равнялась 333 футам.

Спасибо за внимание!

Скачать презентацию МБОУ классическая гимназия 1 им В Г

геометрия гарькина.pptx

Количество слайдов: 8