21d5e0d0edfe01f0fae81513c85e33fb.ppt
- Количество слайдов: 11

MBA 299 – Section Notes 4/11/03 Haas School of Business, UC Berkeley Rawley

AGENDA Administrative Exercises 1. Finish off Exercises from Introduction to Game Theory & The Bertrand Trap • Problem 2 (see last weeks section notes) • Problem 5 d. • Problem 6 • Problem 7 (done on the board) 2. Cournot duopoly 3. Backwards induction problems

ADMINISTRATIVE In response to your feedback – Slides in section – More math CSG entries due Tuesday and Friday at midnight each week Contact info: – rawley@haas. berkeley. edu Office hours Room F 535 – Monday 1 -2 pm – Friday 2 -3 pm

PROOF THAT ALL IDSDS ARE NE (PROBLEM #5 D) Proof by contraction: 1. Assume not => a NE strategy is eliminated by IDSDS 2. Suppose in a two player game strategies s 1, s 2 are a NE 3. WOLOG Let s 1 be the first of the strategies to be eliminated by IDSDS 4. Then there must exist a strategy si that has not yet been eliminated from the strategy set that strictly dominates s 1 5. Therefore U(s 1, s 2) < U(si, s 2) 6. A contradiction of the definition of NE since s 1 must be a best response to s 2 (Q. E. D. ) Source: Robert Gibbons, “Game Theory for Applied Economists” (1992) p. 13

BERTRAND TRAP PROBLEM 6 (I) Parts a and b Part a. ) K 1=K 2=50 0 if pn>$5 dn = 50 if pn=$5, 50 if pn<$5 n=1, 2 profit = 50*(pn-1) max profit by choosing pn=$5 (no game) Part b. ) K 1=K 2=100 dn = 0 if pn> pmin 50 if pn= pmin 100 if pn< pmin profit = X*(pn-1) max profit by choosing pn=C=$1. . .

BERTRAND TRAP PROBLEM 6 Part b continued and Part c Part b. Why does P=C in party b, where K 1=K 2=100? Because 50*(P-delta)+50*(P-delta) > 50*P if delta is small Therefore “defecting” is always the rule until P=C Part c. K 1=100, K 2=50 => there is no pure strategy NE Why? If player 2 charges P 2=C (and earns zero), player 1 can charge C<P 1<=$5 and earn 50*(P 1 -C) But if player 1 charges P 1>C then player 2 will want to increase his price to P 2 = P 1 –e earning 50*(P 2 -C). . . But now, if P 2>C, player 1 will want to charge P 1=P 2 –e earning 100*(P 1 -C) And so and on. . .

COURNOT DUOPOLY Math Set-up P(Q) = a – Q (inverse demand) Q = q 1 + q 2 Ci(qi) = cqi (no fixed costs) Assume c < a Firms choose their q simultaneously Solution Profit i (q 1, q 2) = qi[P(qi+qj)-c] =qi[a-(qi+qj)-c] Recall NE => max profit for i given j’s best play So F. O. C. for qi, assuming qj<a-c qi*=1/2(a-qj*-c) Solving the pair of equations q 1=q 2=(a-c)/3 Note that qj < a – c as we assumed

COURNOT DUOPOLY Intuition Observe that the monopoly outcome is qm=(a-c)/2 profit m = (a-c)2/4 The optimal outcome for the two firms would be to divide the market at the monopoly output level (for example qi=qj=qm/2) But each firm has a strong incentive to deviate at this qm – Check: qm/2 is not firm 2’s best response to qm/2 by firm 1
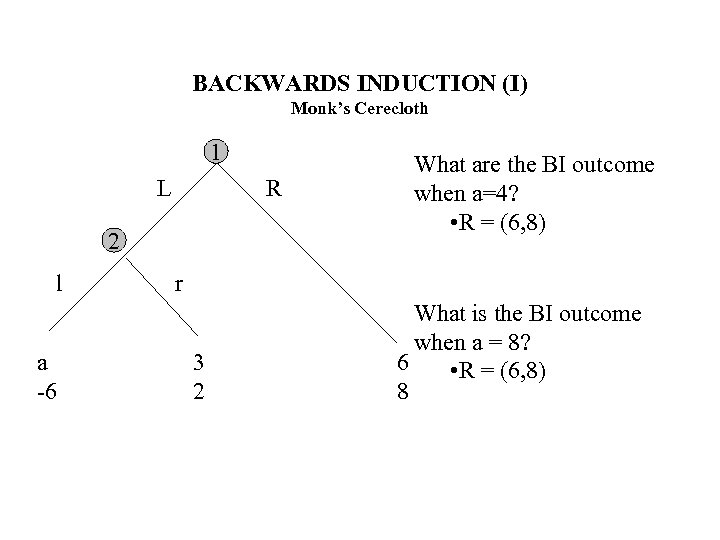
BACKWARDS INDUCTION (I) Monk’s Cerecloth 1 L R 2 l a -6 What are the BI outcome when a=4? • R = (6, 8) r 3 2 What is the BI outcome when a = 8? 6 • R = (6, 8) 8
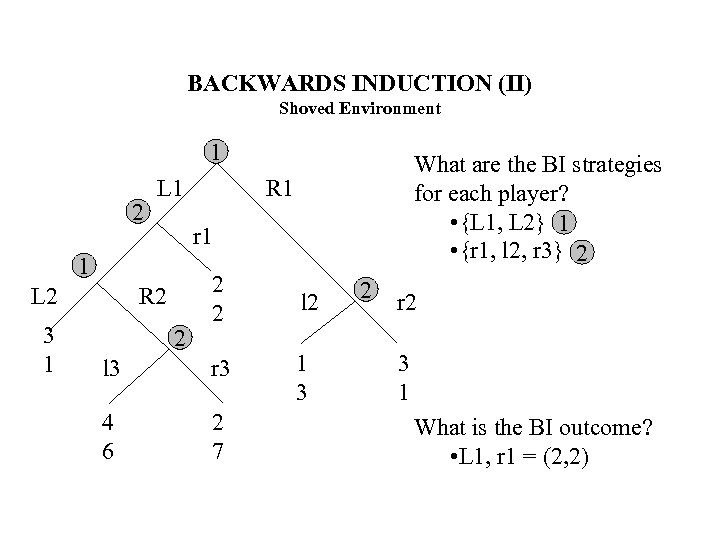
BACKWARDS INDUCTION (II) Shoved Environment 1 2 L 1 R 1 r 1 1 2 2 l 3 r 3 1 3 4 6 2 7 L 2 3 1 What are the BI strategies for each player? • {L 1, L 2} 1 • {r 1, l 2, r 3} 2 R 2 2 2 r 2 3 1 What is the BI outcome? • L 1, r 1 = (2, 2)
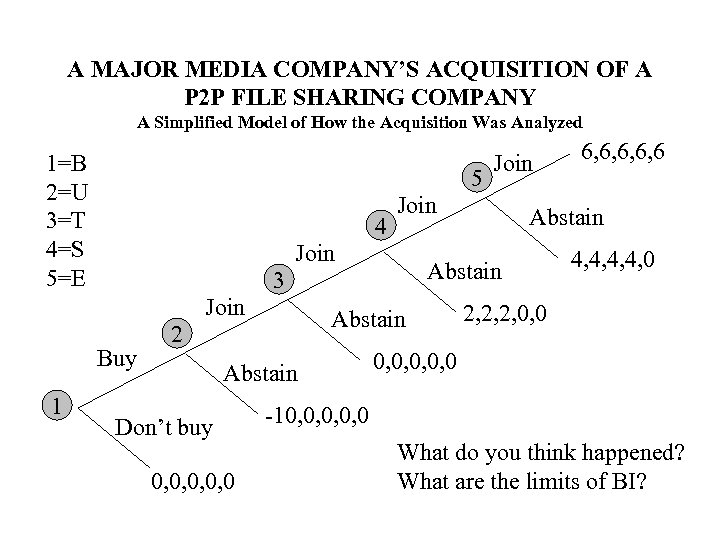
A MAJOR MEDIA COMPANY’S ACQUISITION OF A P 2 P FILE SHARING COMPANY A Simplified Model of How the Acquisition Was Analyzed 1=B 2=U 3=T 4=S 5=E 5 4 Abstain 2 Abstain Don’t buy 0, 0, 0 6, 6, 6 Abstain 3 Buy 1 Join 4, 4, 0 2, 2, 2, 0, 0, 0 -10, 0, 0 What do you think happened? What are the limits of BI?
21d5e0d0edfe01f0fae81513c85e33fb.ppt