MBA 201 a Strategic Thinking Overview

MBA 201 a: Strategic Thinking

Overview – Context: You’re in an industry with a small number of competitors. You’re concerned that if you cut your price, your competitors will, too. How do you act? – The same reasoning applies for pretty much any strategic decision: • Capacity expansion, • Entry and exit, • Product positioning, • Advertising expenditures, etc. Professor Wolfram MBA 201 a - Fall 2009 Page 1

Short digression on the term “strategy” Strategy includes: – Organizational structure and processes needed to implement the firm’s plan. – Boundaries of the firm: scale, scope, extent of outsourcing. – Formal analysis of interactions between competitors: game theory. Professor Wolfram MBA 201 a - Fall 2009 Page 2

We will apply the tools of game theory Informally, game theory reminds us to: – Understand our competitors. Our results depend not only on our own decisions but on our competitors’ decisions as well. – Look into the future. Decisions taken today may have an impact in future decisions, both by ourselves and by our competitors. – Pay attention to information. Who knows what can make a difference. – Look for win-win opportunities. Some situations are competitive, but others offer benefits to all. Professor Wolfram MBA 201 a - Fall 2009 Page 3

The E. T. “chocolate wars” In the movie E. T. a trail of Reese's Pieces, one of Hershey's chocolate brands, is used to lure the little alien into the house. As a result of the publicity created by this scene, sales of Reese's Pieces tripled, allowing Hershey to catch up with rival Mars. Professor Wolfram MBA 201 a - Fall 2009 Page 4

Chocolate wars…the details – Universal Studio's original plan was to use a trail of Mars’ M&Ms and charge Mars $1 mm for the product placement. – However, Mars turned down the offer, presumably because it thought $1 mm was high. – The producers of E. T. then turned to Hershey, who accepted the deal, which turned out to be very favorable to them (and unfavorable to Mars). Professor Wolfram MBA 201 a - Fall 2009 Page 5

Formal analysis of the chocolate wars Suppose: – Publicity from the product placement would have increased Mars’ profits by $800, 000. – Hershey's increase in market share cost Mars $500, 000. – Benefit to Hershey from having its brand featured is given by b. – Hershey knows the value of b. Mars knows only that b=$1, 200, 000 or b=$700, 000 with equal probability. Professor Wolfram MBA 201 a - Fall 2009 Page 6

Mars 1: decision approach buy [-200] M not buy [0] Professor Wolfram MBA 201 a - Fall 2009 Page 7

Mars 2: naïve game theory Payoff to Mars Payoff to Hershey buy [-200, 0] Payoff to Hershey = M . 5 x(1. 2 M-1 M) +. 5(. 7 M-1 M) not buy 0 H not buy Professor Wolfram [-500, -50] MBA 201 a - Fall 2009 [0, 0] Page 8

Mars 3: real game theory [-200, 0] buy -500 M b = 1200 (50%) not buy -250 buy H not buy [0, 0] N b = 700 (50%) 0 buy MBA 201 a - Fall 2009 [-500, -300] H not buy Professor Wolfram [-500, 200] [0, 0] Page 9

Mars: summary – Think about your competitor: Mars should think about Hershey, and vice versa. – Timing matters: Hershey had the last move. – Information matters: Hershey has more information than Mars, and in this example it made a difference. – Key business insight: part of the benefit to Mars was to keep the opportunity from Hershey. Professor Wolfram MBA 201 a - Fall 2009 Page 10

Game theory: concepts – What are the elements of a game? • Players (in previous example: Mars and Hershey) • Rules (sequentially respond to Universal’s offer) • Strategies (Yes or No) • Payoffs (sales minus payment to Universal) – What can I do with it? • Determine how good each of my strategies is • Figure out what my rival is probably going to do Professor Wolfram MBA 201 a - Fall 2009 Page 11

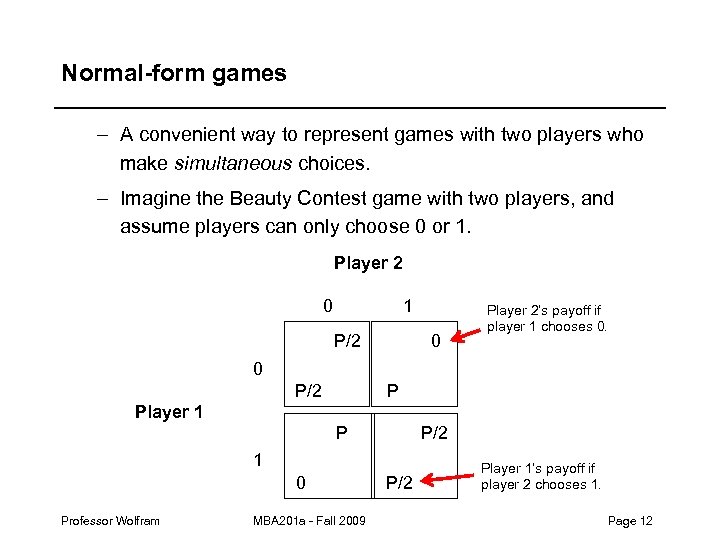
Normal-form games – A convenient way to represent games with two players who make simultaneous choices. – Imagine the Beauty Contest game with two players, and assume players can only choose 0 or 1. Player 2 0 1 P/2 0 Player 2’s payoff if player 1 chooses 0. 0 P/2 P Player 1 P/2 P 1 0 Professor Wolfram MBA 201 a - Fall 2009 P/2 Player 1’s payoff if player 2 chooses 1. Page 12

Dominant/dominated strategies – Dominant strategy: payoff is greater than any other strategy regardless of rival’s choice. • Rule 1: if there is one, choose it. – Dominated strategy: payoff is lower than some other strategy regardless of rival’s choice. • Rule 2: do not choose dominated strategies. Professor Wolfram MBA 201 a - Fall 2009 Page 13

Outcomes of games – Sometimes a game can be “solved” just by looking at dominant and dominated strategies (e. g. , example above). – However, there are many games for which this isn’t enough to produce an outcome. – Nash equilibrium: Combination of moves in which no player would want to change her strategy unilaterally. Each chooses its best strategy given what the others are doing. Professor Wolfram MBA 201 a - Fall 2009 Page 14

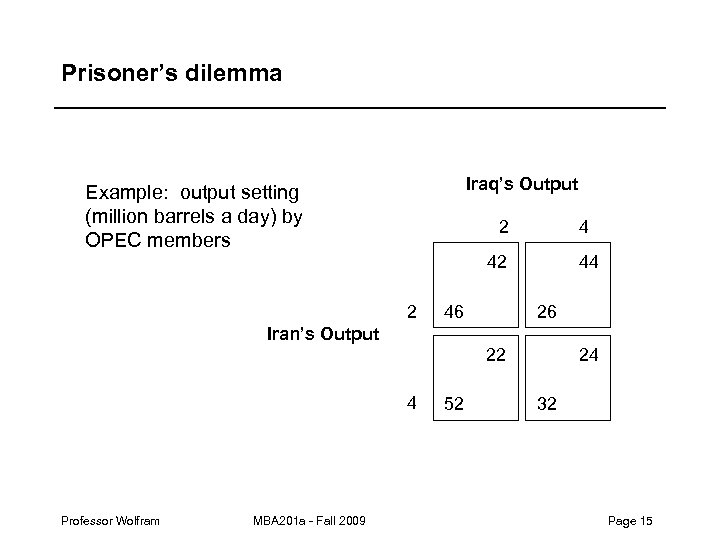
Prisoner’s dilemma Iraq’s Output Example: output setting (million barrels a day) by OPEC members 2 4 42 2 46 44 26 Iran’s Output 22 4 Professor Wolfram MBA 201 a - Fall 2009 52 24 32 Page 15

Prisoner’s dilemma… – Dominant strategies: high output. – Equilibrium payoffs are (32, 24), much worse than would be attained by low output, (46, 42). – Conflict between individual incentives and joint incentives. – Typical of many business situations. – Are cartels inherently unstable? Professor Wolfram MBA 201 a - Fall 2009 Page 16

Auctions – Remember we said that games involved players, rules and payoffs? – In auctions, the rules of the game, and how players’ choices affect their payoffs, are very well-defined. – Auctions have become relevant in a number of business contexts. Professor Wolfram MBA 201 a - Fall 2009 Page 17

Common auction mechanisms – English auction (a. k. a. oral ascending auction). Price is successively raised until only one bidder remains. • Antiques, Artwork, Wine • Used cars – Sealed-bid first-price auction (or simply first-price auction). Highest/lowest bid is selected and pays/receives that value. • Mineral rights • Building contracts Professor Wolfram MBA 201 a - Fall 2009 Page 18

More auction mechanisms – Dutch auction (a. k. a. oral descending auction). Price is successively decreased until one bidder calls. • Flowers, tobacco, fish • Privatizations – Second price auction (a. k. a. Vickrey auction). Just like first price auction, but: winner pays price equal to second highest bid. • e. Bay • Stamps and other collectibles • Radio spectrum rights in New Zealand Professor Wolfram MBA 201 a - Fall 2009 Page 19

Bidding strategies vary by auction type – Optimal bidding strategy in second-price auction is to bid own value. – Optimal bidding strategy in English auction is to continue bidding up to own valuation. – What about in a Dutch or sealed-bid auction? – … beware the Winner’s Curse. Professor Wolfram MBA 201 a - Fall 2009 Page 20

Winner’s Curse example – Example: bids for oil-track auction – True, common, value of object is X. – Each bidder i estimates that value is X + ei. – Average ei is zero: bidders’ estimates are unbiased. – Suppose each bidder bids his or her valuation minus some margin mi. – Winning bid will correspond to highest ei, i. e. , winner will be the most “optimistic” bidder. – If mi is not sufficiently large, i. e. , if mi < ei, then winner will lose money (bids more than true value). Professor Wolfram MBA 201 a - Fall 2009 Page 21

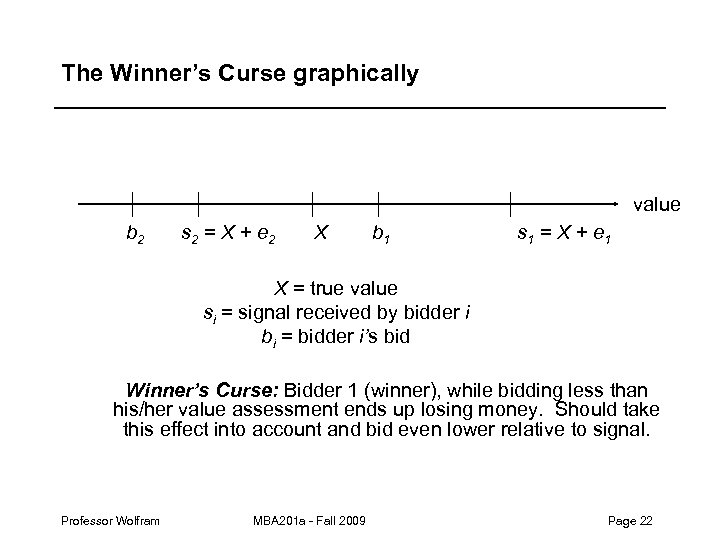
The Winner’s Curse graphically value b 2 s 2 = X + e 2 X b 1 s 1 = X + e 1 X = true value si = signal received by bidder i bi = bidder i’s bid Winner’s Curse: Bidder 1 (winner), while bidding less than his/her value assessment ends up losing money. Should take this effect into account and bid even lower relative to signal. Professor Wolfram MBA 201 a - Fall 2009 Page 22

Comparing auction mechanisms – If valuations are independent and bidders are similar and risk neutral, then all of the above auction mechanisms induce the same average seller revenue. – If valuations are correlated (extreme: common value), then the English auction implies higher average revenue than the sealed-bid auction. – Collusion among bidders easier with English auction. – Transactions costs vary across auctions. Professor Wolfram MBA 201 a - Fall 2009 Page 23

Takeaways – Game theory is a formal approach to strategy. – Highlights impact of strategic interactions among firms or other “players. ” – Forces you to consider your competitors’ choices. – Auctions lend themselves well to game-theoretic analysis. – Concepts: players, strategies, dominant and dominated strategies, best responses, Nash equilibrium. – Stay tuned for another example on Thursday… Professor Wolfram MBA 201 a - Fall 2009 Page 24