Matrix methods in paraxial optics Wednesday September 25, 2002 1
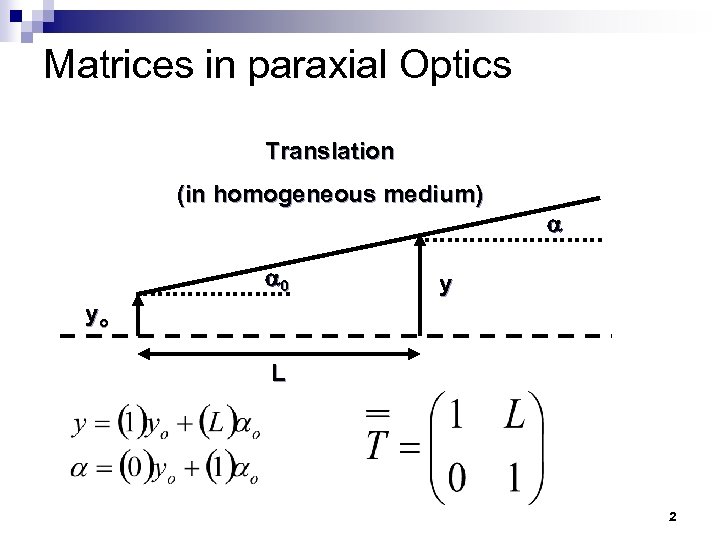
Matrices in paraxial Optics Translation (in homogeneous medium) 0 y yo L 2
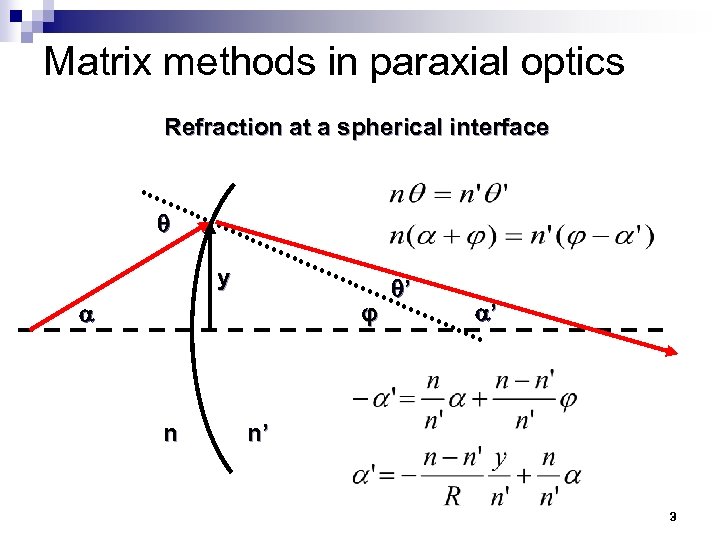
Matrix methods in paraxial optics Refraction at a spherical interface y φ n ’ ’ n’ 3
Matrix methods in paraxial optics Refraction at a spherical interface y φ n ’ ’ n’ 4
Matrix methods in paraxial optics Lens matrix n n. L n’ For the complete system Note order – matrices do not, in general, commute. 5
Matrix methods in paraxial optics 6
Matrix properties 7
Matrices: General Properties For system in air, n=n’=1 8
System matrix 9
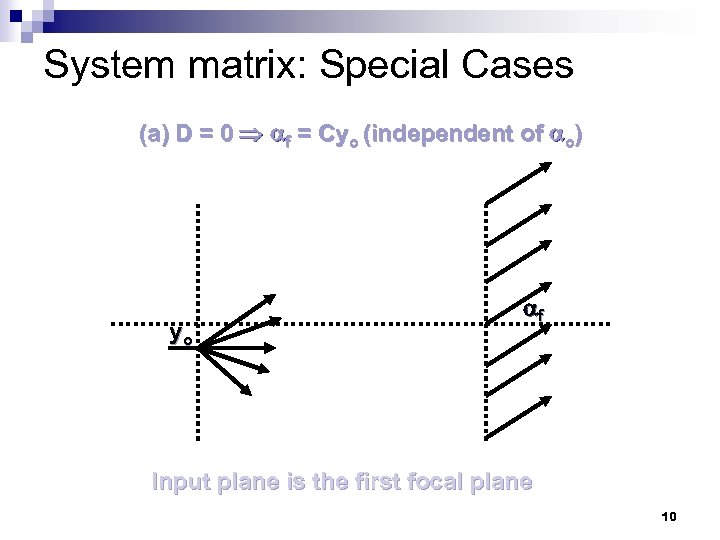
System matrix: Special Cases (a) D = 0 f = Cyo (independent of o) yo f Input plane is the first focal plane 10
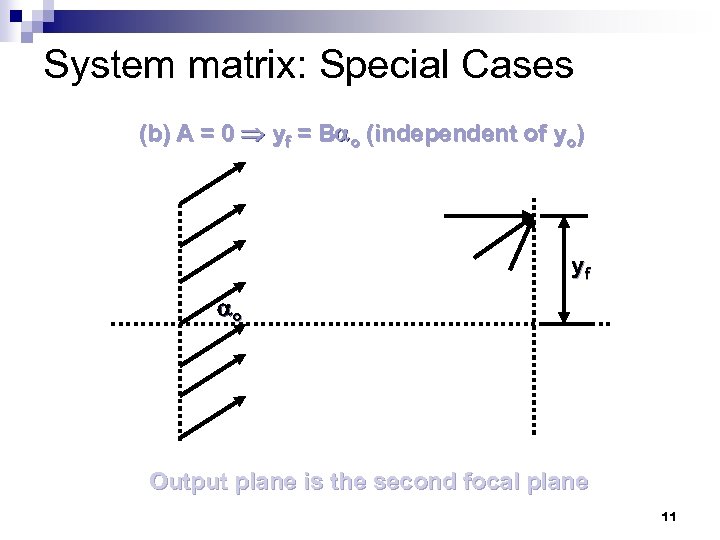
System matrix: Special Cases (b) A = 0 yf = B o (independent of yo) yf o Output plane is the second focal plane 11
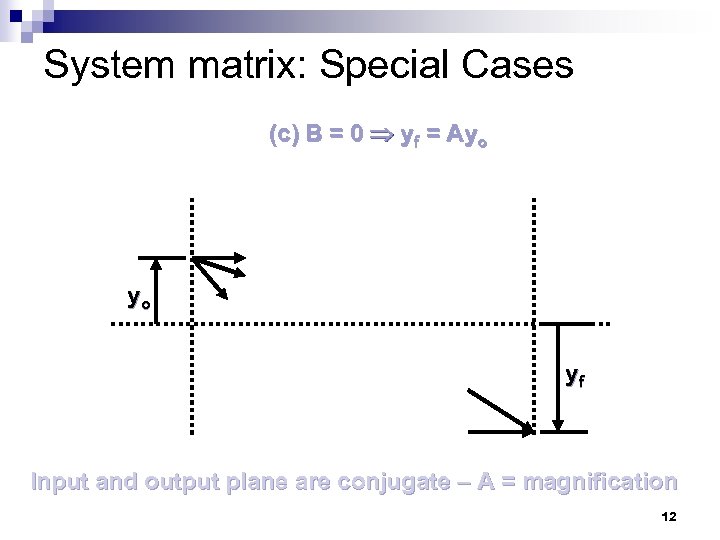
System matrix: Special Cases (c) B = 0 yf = Ayo yo yf Input and output plane are conjugate – A = magnification 12
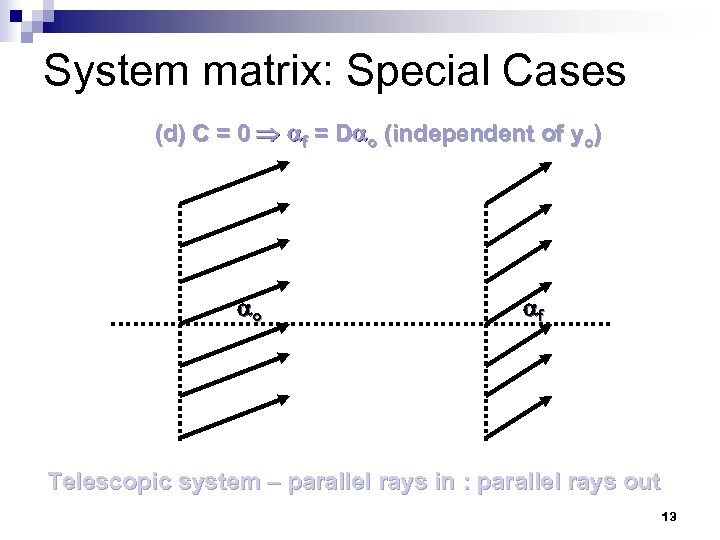
System matrix: Special Cases (d) C = 0 f = D o (independent of yo) o f Telescopic system – parallel rays in : parallel rays out 13
Examples: Thin lens Recall that for a thick lens For a thin lens, d=0 14
Examples: Thin lens Recall that for a thick lens For a thin lens, d=0 In air, n=n’=1 15
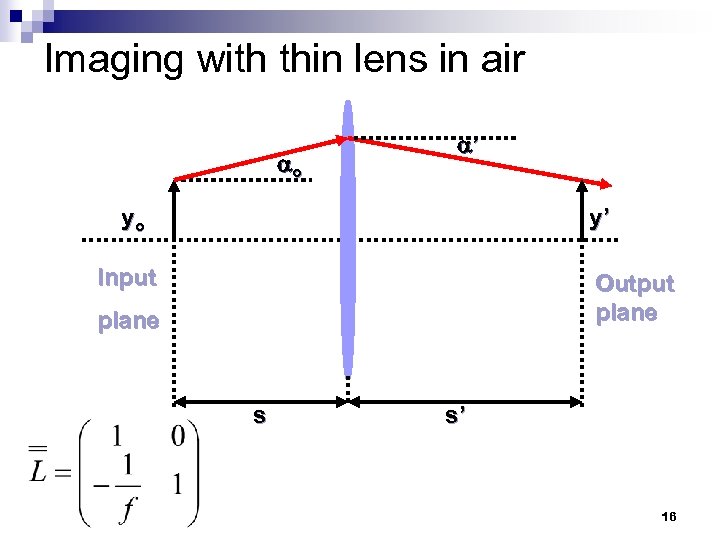
Imaging with thin lens in air o ’ yo y’ Input Output plane s s’ 16
Imaging with thin lens in air For thin lens: A=1 B=0 D=1 C=-1/f y’ = A’yo + B’ o 17
Imaging with thin lens in air For thin lens: A=1 B=0 D=1 C=-1/f y’ = A’yo + B’ o For imaging, y’ must be independent of o B’ = 0 B’ = As + B + Css’ + Ds’ = 0 s + 0 + (-1/f)ss’ + s’ = 0 18
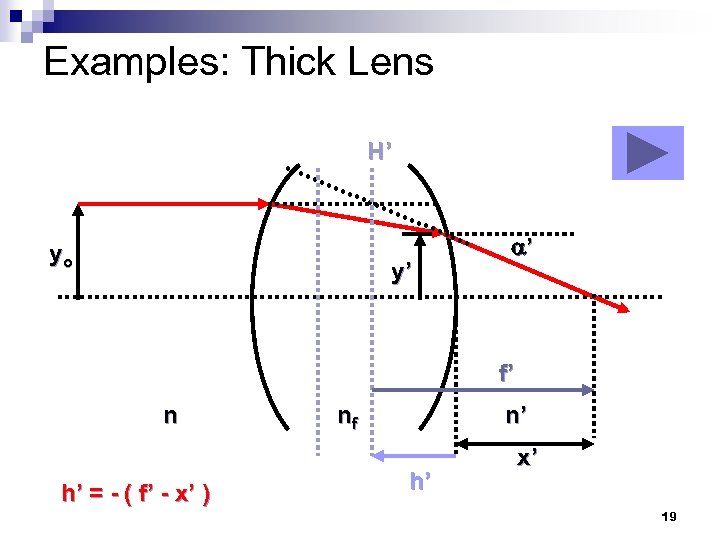
Examples: Thick Lens H’ yo y’ ’ f’ n h’ = - ( f’ - x’ ) nf n’ h’ x’ 19
Cardinal points of a thick lens 20
Cardinal points of a thick lens 21
Cardinal points of a thick lens Recall that for a thick lens As we have found before h can be recovered in a similar manner, along with other cardinal points 22
Скачать презентацию Matrix methods in paraxial optics Wednesday September 25
d14d8cf1483f83f24b4af2cd89d49a8e.ppt