МАТРИЦЫ ВЛИЯНИЯ Игнатюк В И Игнатов А Ю

МАТРИЦЫ ВЛИЯНИЯ Игнатюк В. И. Игнатов А. Ю.

Матричная форма расчетов В ряде случаев расчеты конструкций и сооружений удобно производить в матричной форме. Такая форма позволяет более компактно записывать формулы и уравнения, а также удобна для компьютерных расчетов.

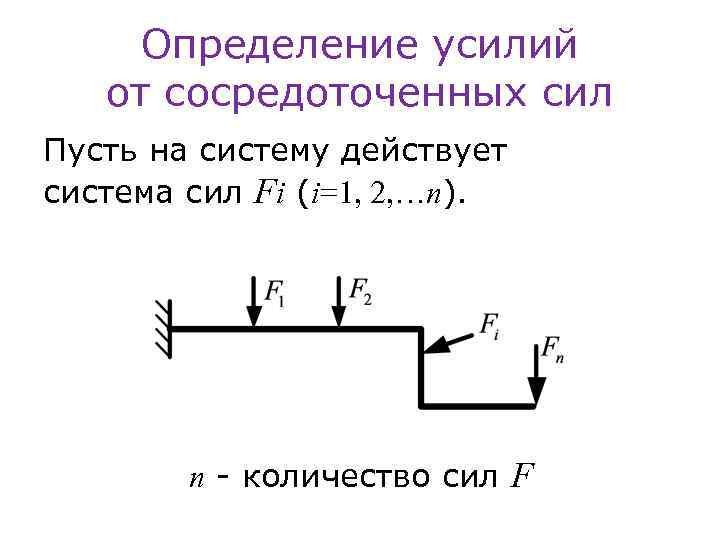Определение усилий от сосредоточенных сил Пусть на систему действует система сил Fi (i=1, 2, …n). n - количество сил F

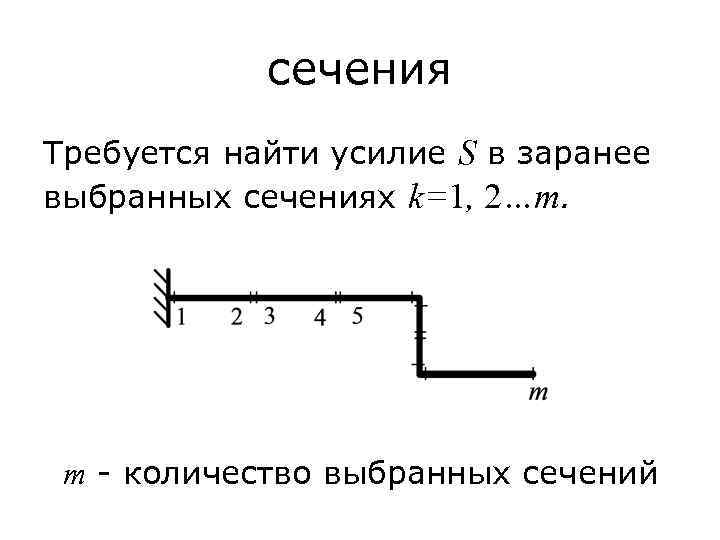сечения Требуется найти усилие S в заранее выбранных сечениях k=1, 2…m. m - количество выбранных сечений

На основании принципа независимости действия сил уравнения для определения интересующих нас усилий можно записать в виде:

ski – силовой фактор в сечении k, вызванный единичной силой, приложенной по направлении Fi. То есть первый индекс (k) показывает, где вычисляется усилие, а второй индекс (i) – от чего.

В матричной форме эта система записывается так: - вектор искомых внутренних усилий:

В матричной форме эта система записывается так: - вектор внешних сил:

В матричной форме эта система записывается так: - матрица влияния фактора S порядка m x n:

В общем случае и матрица [LS] несимметрична.

Если отыскиваются изгибающие моменты в сечениях балки или рамы, то S = M, а матрица [LS] называется матрицей влияния изгибающих моментов и обозначается [LM]. При определении продольных усилий в стержнях фермы S = N, матрица [LS] – матрица влияния продольных усилий (обозн. [LN]).

Формирование матрицы влияния Всякий i-й столбец матрицы влияния [LS] может быть получен как значения усилия S от единичной силы, приложенной в точке i (при силах Fi любых направлений).

Всякая k-я строка матрицы влияния [LS] может быть получена через линию влияния усилия S в сечении k (л. в. Sk), построенную от единичного груза F=1, параллельного данным силам. (при силах Fi одного направления).

Следовательно, каждый столбец матрицы является аналогом соответствующей единичной эпюры (при внешних силах любых направлений); каждая строка – аналогом соответствующей линии влияния (при силах одного направления):

Формирование матрицы влияния

На практике часто встречается загружение конструкции вертикальными сосредоточенными силами. При этом матрицу влияния можно сформировать двумя способами: 1) по столбцам – с помощью единичных эпюр; 2) по строкам – с помощью линий влияния.

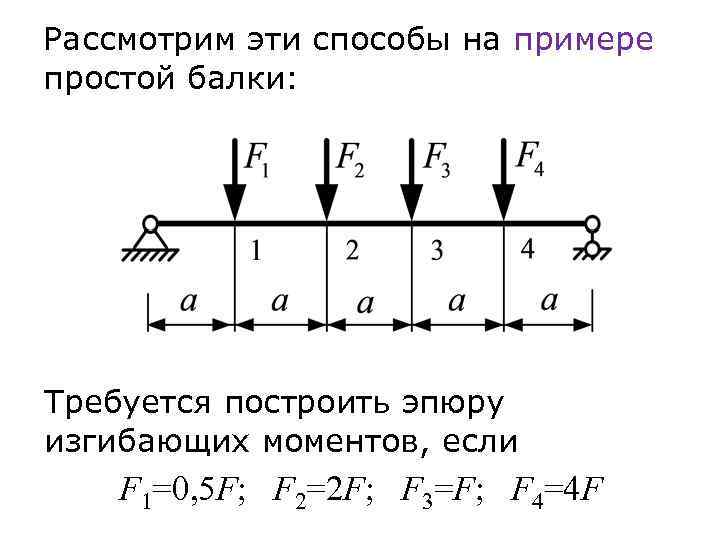Рассмотрим эти способы на примере простой балки: Требуется построить эпюру изгибающих моментов, если F 1=0, 5 F; F 2=2 F; F 3=F; F 4=4 F

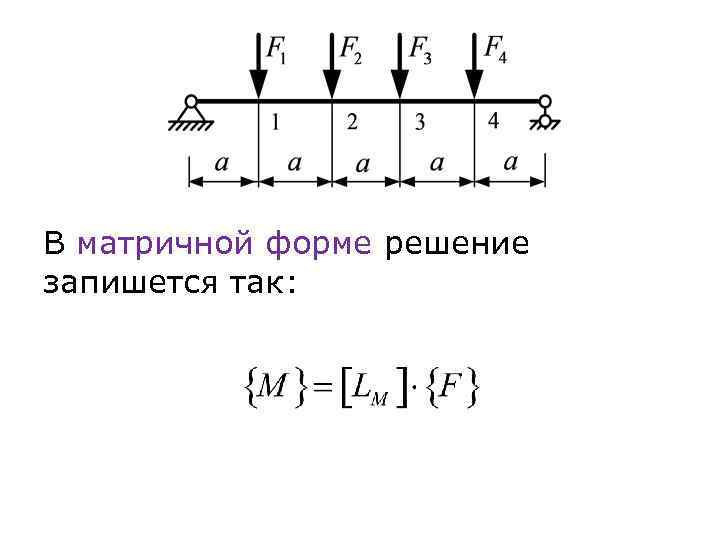В матричной форме решение запишется так:

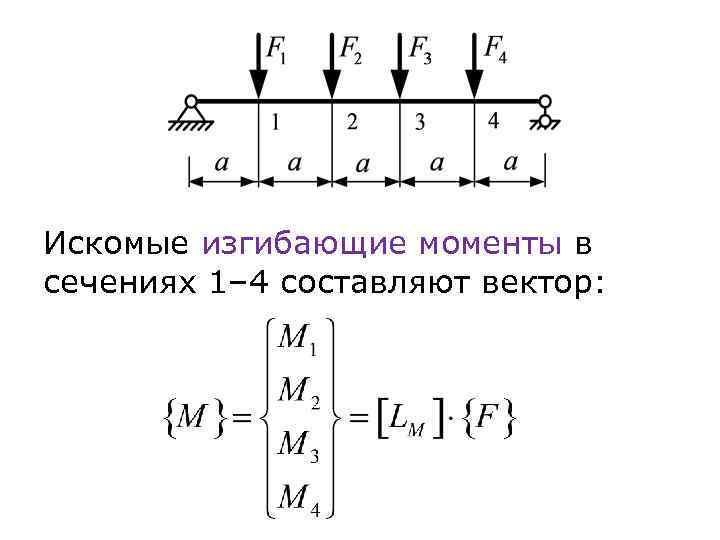Искомые изгибающие моменты в сечениях 1– 4 составляют вектор:

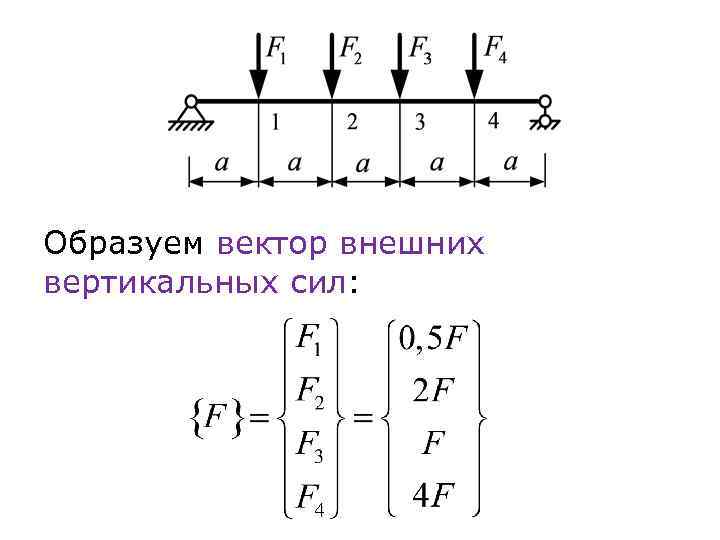Образуем вектор внешних вертикальных сил:

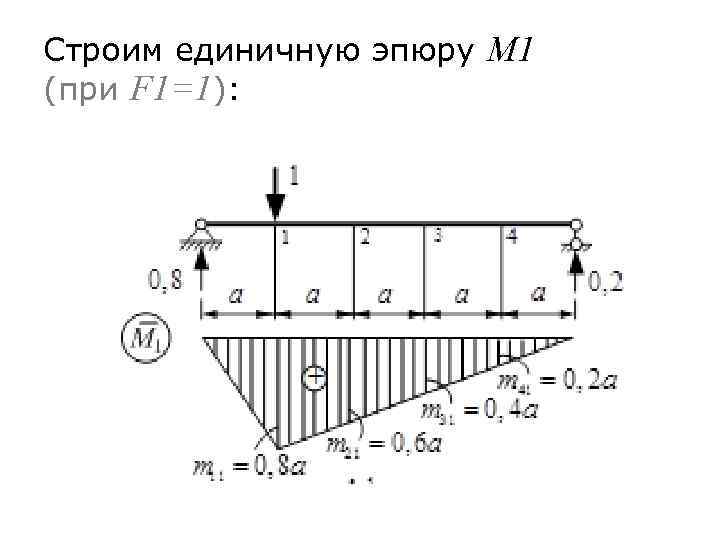Строим единичную эпюру M 1 (при F 1=1):

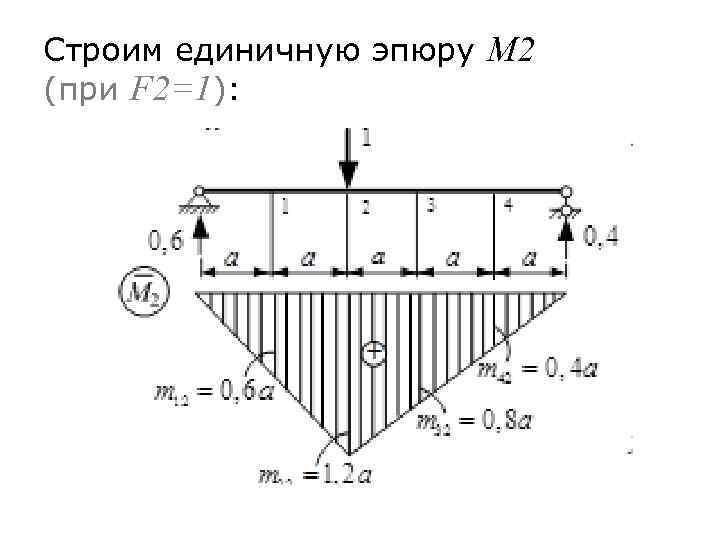Строим единичную эпюру M 2 (при F 2=1):

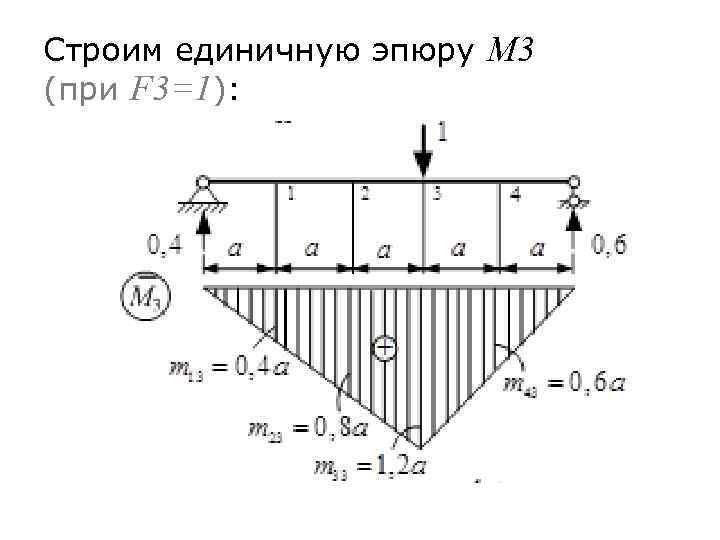Строим единичную эпюру M 3 (при F 3=1):

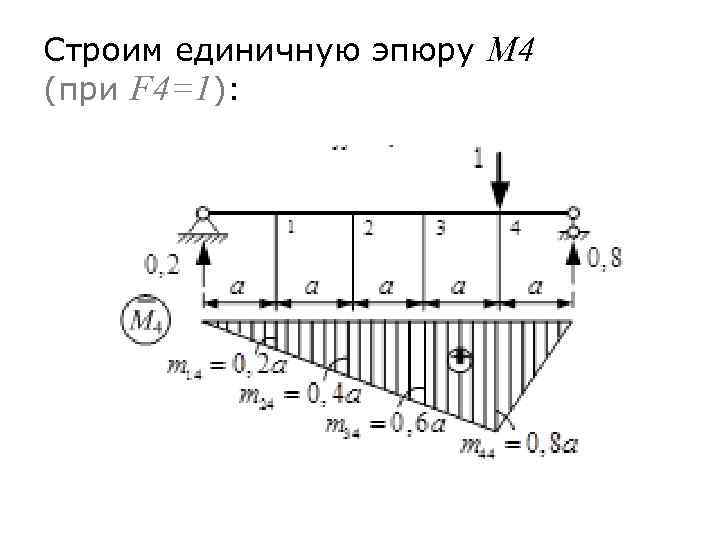Строим единичную эпюру M 4 (при F 4=1):

Составляем матрицу влияния, используя значения с единичных эпюр:

Вычисляем:

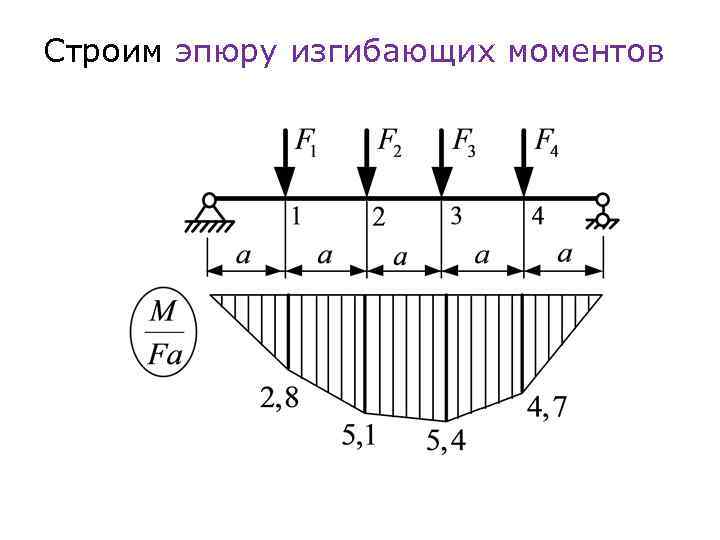Строим эпюру изгибающих моментов

Заметим, что матричная форма расчета особенно удобна при исследовании нескольких вариантов загружения одной и той же системы. Если значения внешних сил изменятся, новые значения внутренних сил легко найти, умножив матрицу влияния [LS] на новый вектор {F}.