Матрицы и операции над ними

Матрицы и операции над ними

План изложения темы 1. Основные сведения о матрицах : n Понятие матрицы n Виды матриц 2. Операции над матрицами: n Умножение на число n Сложение n Умножение матриц n Возведение в степень n Транспонирование 3. Обратная матрица

Литература n Высшая математика для экономистов: Учебник для студентов вузов. Под ред. проф. Н. Ш. Кремера. n Высшая математика для экономистов: Практикум для студентов вузов. Под ред. проф. Н. Ш. Кремера.

Основные сведения о матрицах

Понятие матрицы n Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. n Обозначение матриц: A, B, C, X, … n Числа, составляющие матрицу, называются элементами матрицы. n Обозначение элементов: где i – номер строки, j – номер столбца

Запись матриц n В общем виде n В сокращенной форме

Пример

Виды матриц n Определение: Матрица любого размера называется нулевой или нуль-матрицей, если все ее элементы равны нулю. n Обозначение: О n Пример:

Виды матриц Матрица, размерности: n 1×n называется матрицей-строкой или вектором-строкой n m× 1 называется матрицей-столбцом или вектором-столбцом

Виды матриц n Матрица размерности n×n называется квадратной порядка n n Пример - квадратная матрица второго порядка

Диагональ матрицы n Элементы матрицы, у которых номер столбца равен номеру строки (i=j), называются диагональными и составляют главную диагональ матрицы. n Сумма элементов главной диагонали квадратной матрицы называется её следом. Обозначается tr. A.

Виды квадратных матриц n Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной матрицей. n Пример: - диагональная матрица второго порядка

Виды квадратных матриц n Если у диагональной матрицы порядка n все диагональные элементы равны 1, матрица называется единичной порядка n. n Обозначение En n Пример - единичная матрица третьего порядка

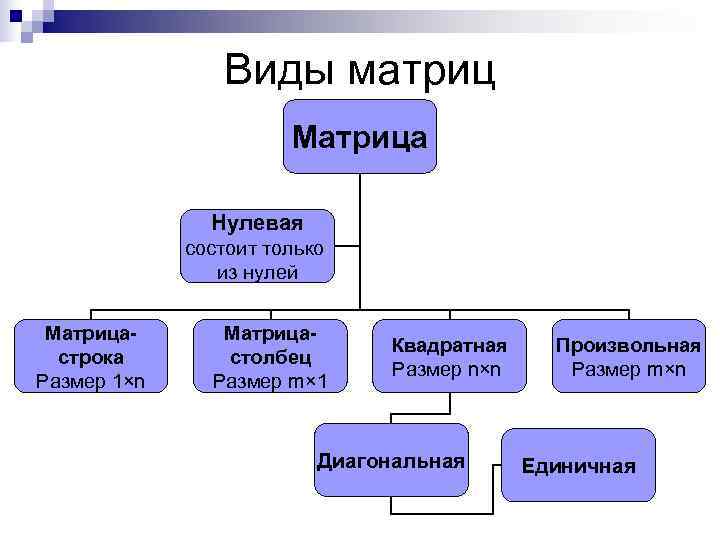
Виды матриц Матрица Нулевая состоит только из нулей Матрица- Квадратная Произвольная строка столбец Размер n×n Размер m×n Размер 1×n Размер m× 1 Диагональная Единичная

Операции над матрицами

Операции над матрицами n Умножение матрицы на число n Сложение матриц n Вычитание матриц n Умножение матриц n Возведение в степень n Транспонирование матрицы

Умножение матрицы на число n Выполнимо для любых матриц и любых чисел n Производится поэлементно n Правило: n Пример:

Сложение матриц n Выполнимо только для матриц одинаковой размерности n Производится поэлементно n Правило: n Пример:

Вычитание матриц n Выполнимо только для матриц одинаковой размерности n Производится поэлементно n Правило: или n Пример:

Умножение матриц n Выполнимо если число столбцов первого множителя равно числу строк второго n Правило: n Примеры:

Возведение в степень n Выполнимо для квадратных матриц n Правила: n Пример:

Транспонирование n Выполнимо для любой матрицы n Обозначение: АТ или А' n Правило: поменять строки на столбцы с сохранением порядка. n Пример:

Обратная матрица n Обозначение: А-1–обратная для матрицы А n Определение: Матрицей А-1, обратной к данной квадратной матрице А, называется такая, что выполняется равенство: А-1∙А = А∙ А-1 = Е. n Пример: -обратна матрице , т. к.