11-Графы-Матрицы графов и их свойства, операции.ppt
- Количество слайдов: 16
 Матрицы графов и их свойства. Матрица смежности.
Матрицы графов и их свойства. Матрица смежности.
 Матрицей смежности (смежностей) А=||aij|| графа G с p вершинами называется (рxр) матрица, в которой аij = 1, если вершина υi смежна с υj, и аij = 0 в противном случае. Итак, существует взаимно однозначноесоответствие между графами с р вершинами и симметрическими бинарными (рxр) – матрицами с нулями на главной диагонали. Суммы элементов матрицы А по строкам равны степеням вершин графа G (ρ(1)=3, ρ(2)=2, ρ(3)=4, ρ(4)=2, ρ(5)=3.
Матрицей смежности (смежностей) А=||aij|| графа G с p вершинами называется (рxр) матрица, в которой аij = 1, если вершина υi смежна с υj, и аij = 0 в противном случае. Итак, существует взаимно однозначноесоответствие между графами с р вершинами и симметрическими бинарными (рxр) – матрицами с нулями на главной диагонали. Суммы элементов матрицы А по строкам равны степеням вершин графа G (ρ(1)=3, ρ(2)=2, ρ(3)=4, ρ(4)=2, ρ(5)=3.
 Матрица смежности орграфа определяется аналогично: А=А(Д)=||aij||, где аij = 1, если дуга υiυj принадлежит Д, и аij = 0 в противном случае. Итак, А(Д) не обязательно симметрична. Матрицу смежности данного графа можно рассматривать как матрицу смежности симметрического орграфа. Линейным подграфом орграфа Д называется подграф, в котором у каждой вершины полустепень исхода и полустепень захода равны 1. Таким образом, такой подграф содержит непересекающийся набор простых контуров. Остовной подграф - подграфа G, содержащий все его вершины.
Матрица смежности орграфа определяется аналогично: А=А(Д)=||aij||, где аij = 1, если дуга υiυj принадлежит Д, и аij = 0 в противном случае. Итак, А(Д) не обязательно симметрична. Матрицу смежности данного графа можно рассматривать как матрицу смежности симметрического орграфа. Линейным подграфом орграфа Д называется подграф, в котором у каждой вершины полустепень исхода и полустепень захода равны 1. Таким образом, такой подграф содержит непересекающийся набор простых контуров. Остовной подграф - подграфа G, содержащий все его вершины.
 Матрица инциденций определяет граф с точностью до изоморфизма. Теорема с связи матрицы смежностей G и матрицы инциденций G. Пусть ВТ – транспонируемая матрица к В. B=||bij||, размерность nxm (n вершин, m дуг). bij = 1, если xi является начальной вершиной дуги aj. bij = -1, если xi является конечной вершиной дуги aj. bij = 0, если xi не является концевой вершиной дуги aj или если aj является петлей.
Матрица инциденций определяет граф с точностью до изоморфизма. Теорема с связи матрицы смежностей G и матрицы инциденций G. Пусть ВТ – транспонируемая матрица к В. B=||bij||, размерность nxm (n вершин, m дуг). bij = 1, если xi является начальной вершиной дуги aj. bij = -1, если xi является конечной вершиной дуги aj. bij = 0, если xi не является концевой вершиной дуги aj или если aj является петлей.
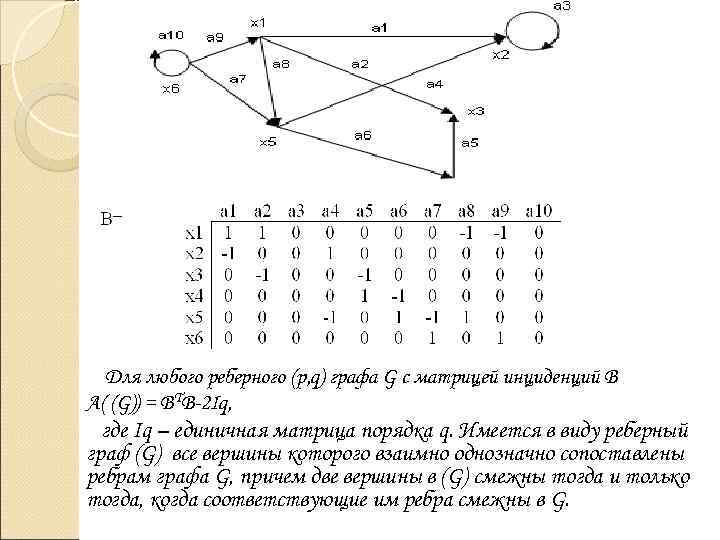 Для любого реберного (p, q) графа G с матрицей инциденций В А( (G)) = BTB-2 Iq, где Iq – единичная матрица порядка q. Имеется в виду реберный граф (G) все вершины которого взаимно однозначно сопоставлены ребрам графа G, причем две вершины в (G) смежны тогда и только тогда, когда соответствующие им ребра смежны в G.
Для любого реберного (p, q) графа G с матрицей инциденций В А( (G)) = BTB-2 Iq, где Iq – единичная матрица порядка q. Имеется в виду реберный граф (G) все вершины которого взаимно однозначно сопоставлены ребрам графа G, причем две вершины в (G) смежны тогда и только тогда, когда соответствующие им ребра смежны в G.
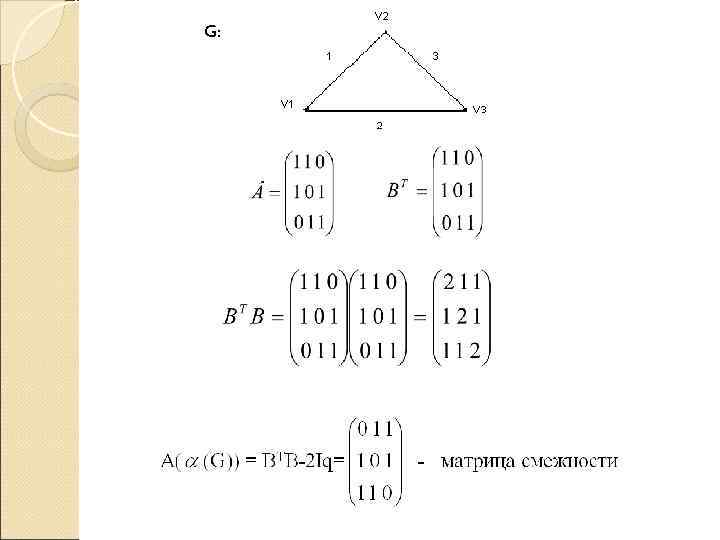 G:
G:
 Построим граф: Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент, равный 1, и один, равный -1, либо все элементы столбца равны 0. Если G – неориентированный граф, то его матрица инциденций определяется также, за исключением того, что все элементы, равные -1, заменяются на +1. Обобщение на случай мультиграфа:
Построим граф: Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент, равный 1, и один, равный -1, либо все элементы столбца равны 0. Если G – неориентированный граф, то его матрица инциденций определяется также, за исключением того, что все элементы, равные -1, заменяются на +1. Обобщение на случай мультиграфа:
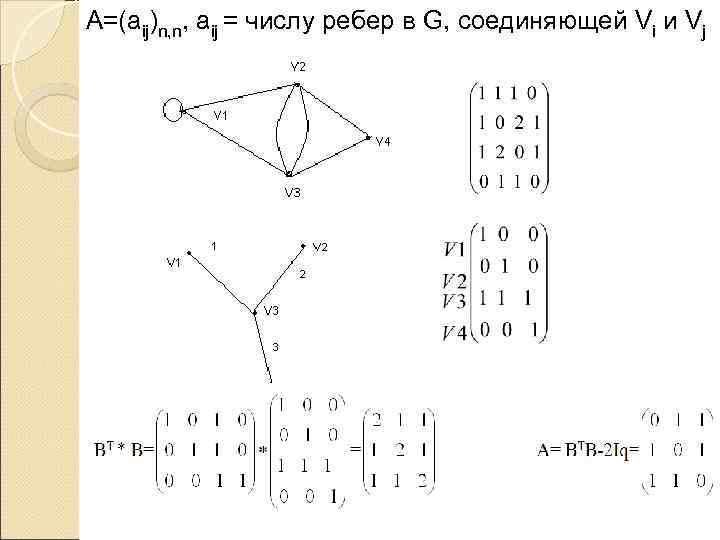 А=(aij)n, n, aij = числу ребер в G, соединяющей Vi и Vj
А=(aij)n, n, aij = числу ребер в G, соединяющей Vi и Vj
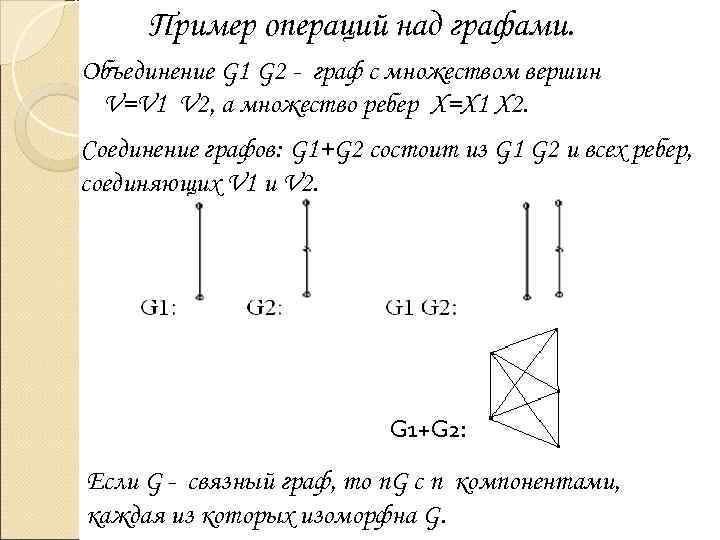 Пример операций над графами. Объединение G 1 G 2 - граф с множеством вершин V=V 1 V 2, а множество ребер Х=Х 1 Х 2. Соединение графов: G 1+G 2 состоит из G 1 G 2 и всех ребер, соединяющих V 1 и V 2. G 1+G 2: Если G - связный граф, то n. G с n компонентами, каждая из которых изоморфна G.
Пример операций над графами. Объединение G 1 G 2 - граф с множеством вершин V=V 1 V 2, а множество ребер Х=Х 1 Х 2. Соединение графов: G 1+G 2 состоит из G 1 G 2 и всех ребер, соединяющих V 1 и V 2. G 1+G 2: Если G - связный граф, то n. G с n компонентами, каждая из которых изоморфна G.
 Пример: Произведение G 1 x. G 2. Рассмотрим 2 вершины U=(U 1, U 2) и V=(V 1, V 2) из V=V 1 x. V 2. Композиция G=G 1[G 2] также имеет V=V 1 x. V 2 в качестве множества вершин и вершина U=(U 1, U 2) смежна с V=(V 1, V 2) тогда и только тогда, когда [U 1 adj V 1] или [U 1=V 1 и U 2 adj V 2]
Пример: Произведение G 1 x. G 2. Рассмотрим 2 вершины U=(U 1, U 2) и V=(V 1, V 2) из V=V 1 x. V 2. Композиция G=G 1[G 2] также имеет V=V 1 x. V 2 в качестве множества вершин и вершина U=(U 1, U 2) смежна с V=(V 1, V 2) тогда и только тогда, когда [U 1 adj V 1] или [U 1=V 1 и U 2 adj V 2]
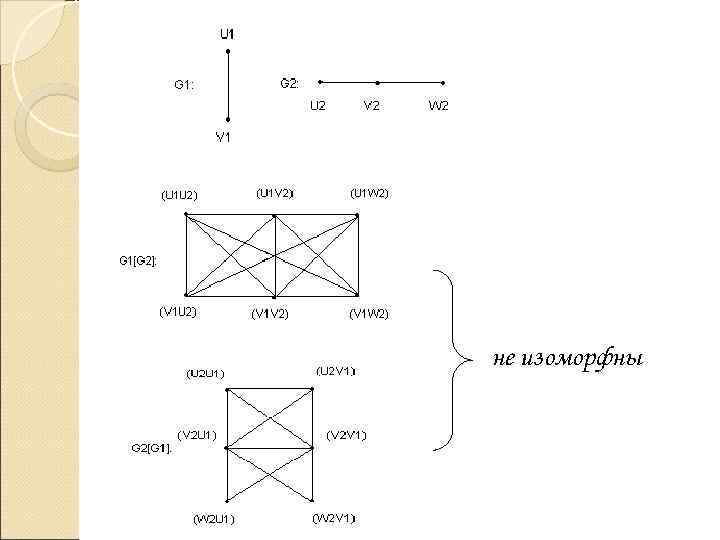 не изоморфны
не изоморфны
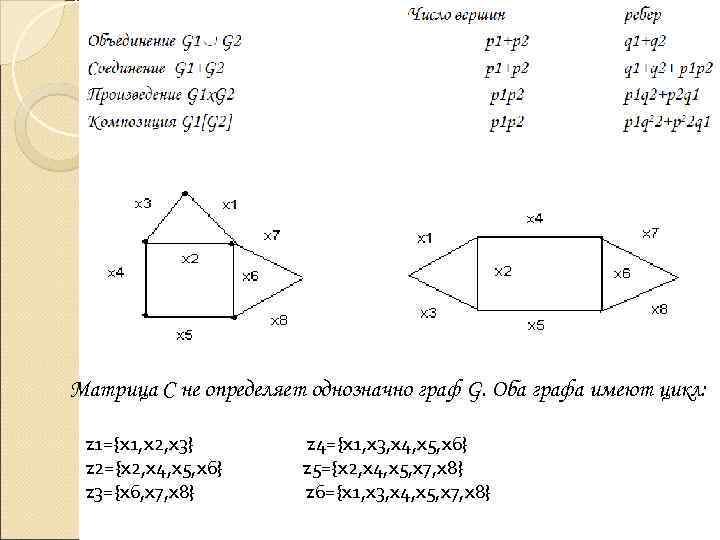 Матрица С не определяет однозначно граф G. Оба графа имеют цикл: z 1={x 1, x 2, x 3} z 4={x 1, x 3, x 4, x 5, x 6} z 2={x 2, x 4, x 5, x 6} z 5={x 2, x 4, x 5, x 7, x 8} z 3={x 6, x 7, x 8} z 6={x 1, x 3, x 4, x 5, x 7, x 8}
Матрица С не определяет однозначно граф G. Оба графа имеют цикл: z 1={x 1, x 2, x 3} z 4={x 1, x 3, x 4, x 5, x 6} z 2={x 2, x 4, x 5, x 6} z 5={x 2, x 4, x 5, x 7, x 8} z 3={x 6, x 7, x 8} z 6={x 1, x 3, x 4, x 5, x 7, x 8}
 Если граф G имеет матрицу инциденций В и матрицу циклов С, то С*ВТ≡ 0(mod 2) Доказательство: рассмотрим i-ю строку матрицы С и j–й столбец матрицы ВТ, которая является j–й строкой матрицы В. Оба 2 -х элемента этих двух строк ≠ 0 тогда и только тогда, когда ребро Х 2 принадлежит i-му циклу Zi и инцидентно 3, вершин Vi. Если цикл Zi содержит Х 2, то он содержит и вершину Vj.
Если граф G имеет матрицу инциденций В и матрицу циклов С, то С*ВТ≡ 0(mod 2) Доказательство: рассмотрим i-ю строку матрицы С и j–й столбец матрицы ВТ, которая является j–й строкой матрицы В. Оба 2 -х элемента этих двух строк ≠ 0 тогда и только тогда, когда ребро Х 2 принадлежит i-му циклу Zi и инцидентно 3, вершин Vi. Если цикл Zi содержит Х 2, то он содержит и вершину Vj.
 Задача: Найти число частей графа с m ребрами. Найти число частей графа с данным числом ребер р. Задача: Даны графы:
Задача: Найти число частей графа с m ребрами. Найти число частей графа с данным числом ребер р. Задача: Даны графы:
![4) Композицию G 1[G 2] и G 2[G 1] 4) Композицию G 1[G 2] и G 2[G 1]](https://present5.com/presentation/3/-128337234_438473741.pdf-img/-128337234_438473741.pdf-15.jpg) 4) Композицию G 1[G 2] и G 2[G 1]
4) Композицию G 1[G 2] и G 2[G 1]
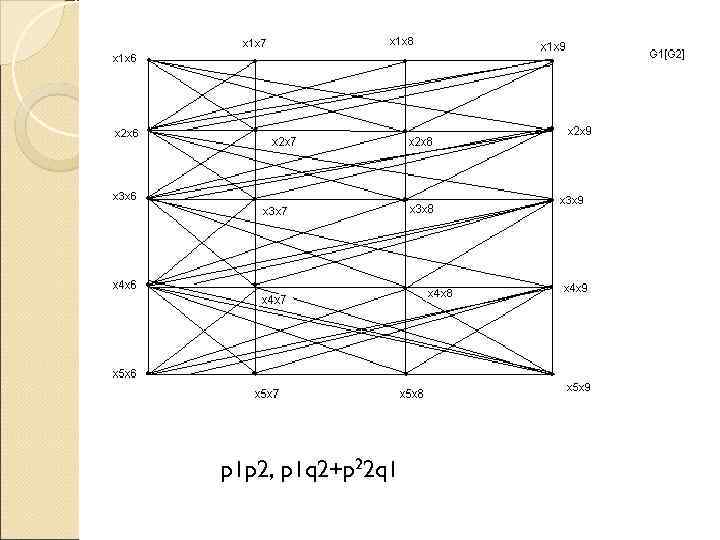 p 1 p 2, p 1 q 2+p 22 q 1
p 1 p 2, p 1 q 2+p 22 q 1


