Матричный подход для стационарного уравнения Шредингера Известно: базис


Матричный подход для стационарного уравнения Шредингера

Известно: базис из стационарных состояний системы с оператором Гамильтона Надо: стационарные состояния системы с Гамильтонианом - невозмущенная (нулевая) задача - возмущение - возмущенная (полная) задача
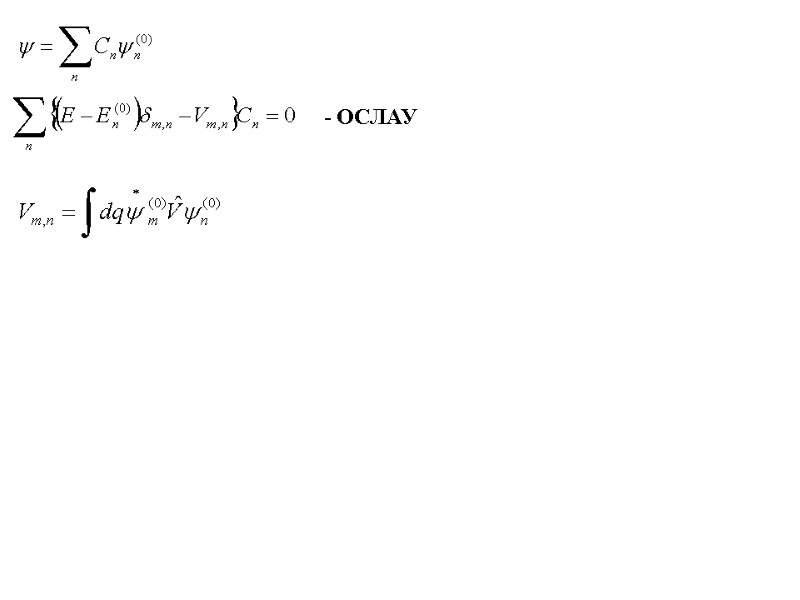
- ОСЛАУ

1) Нулевая задача 2) СУШ в представлении по базису нулевой задачи
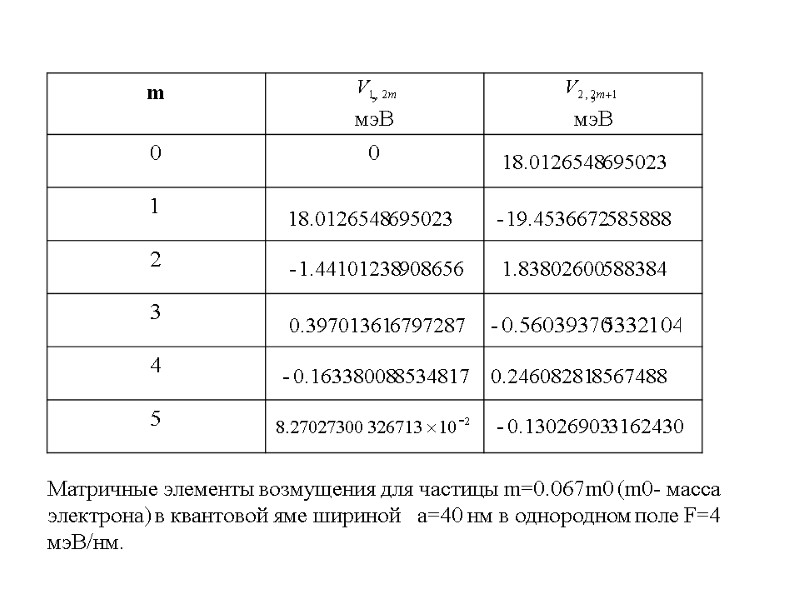
Матричные элементы возмущения для частицы m=0.067m0 (m0- масса электрона) в квантовой яме шириной a=40 нм в однородном поле F=4 мэВ/нм.
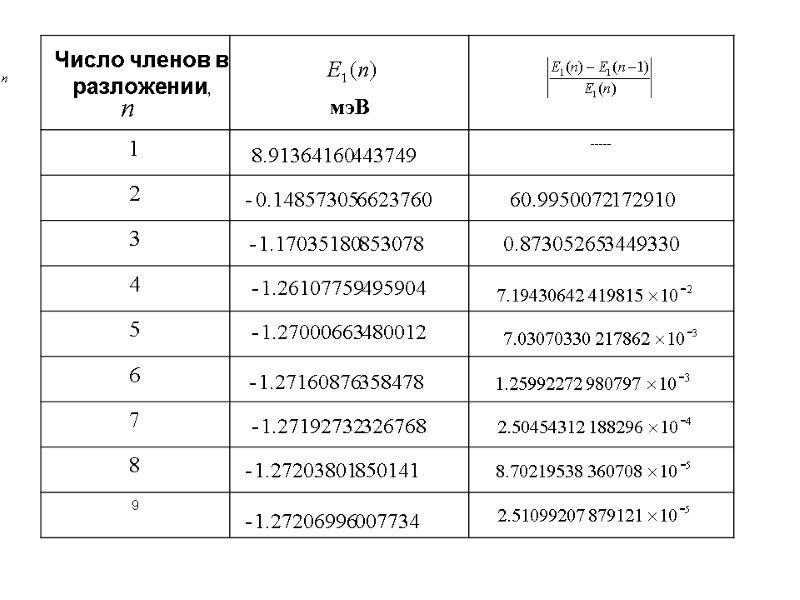
Число членов в разложении,
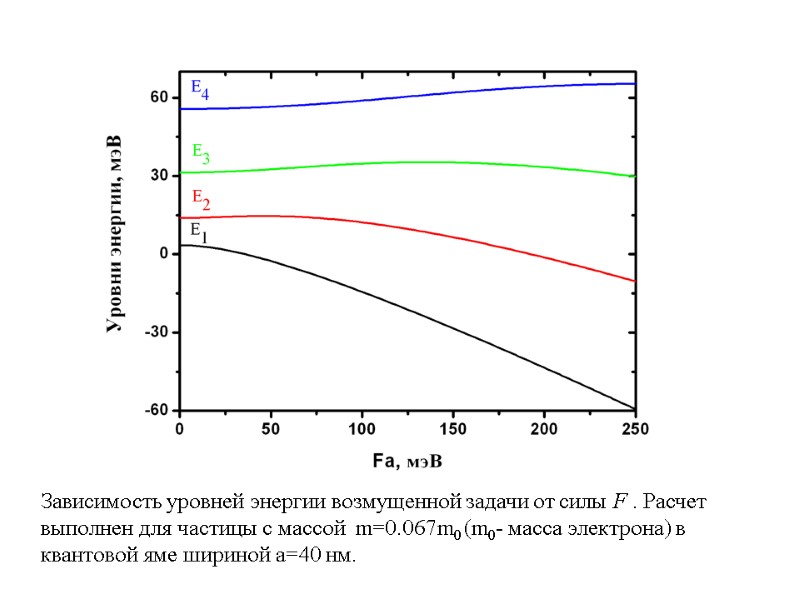
Зависимость уровней энергии возмущенной задачи от силы F . Расчет выполнен для частицы с массой m=0.067m0 (m0- масса электрона) в квантовой яме шириной a=40 нм.

Стационарная теория возмущения в отсутствие вырождения - поправки i-го порядка малости по возмущению
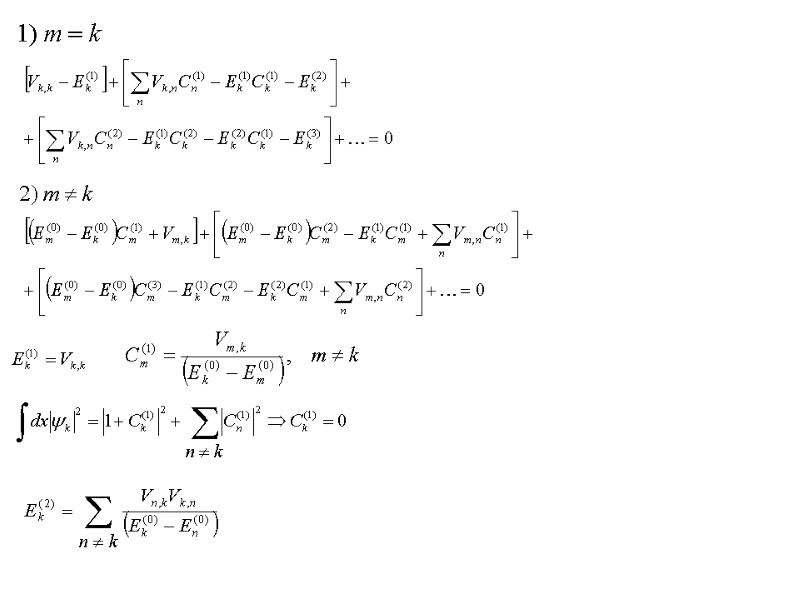
9042-matrichnyy_podkhod_dlya_sush.ppt
- Количество слайдов: 9

