Скачать презентацию Матричные игры Матричная игра — это игра Скачать презентацию Матричные игры Матричная игра — это игра

Решение матричных игр методами ЛП.pptx

  • Количество слайдов: 39

Матричные игры Матричные игры

Матричная игра - это игра двух лиц с нулевой суммой, имеющих конечное число стратегий. Матричная игра - это игра двух лиц с нулевой суммой, имеющих конечное число стратегий. Парная игра с нулевой суммой является антагонистической, так как выигрыш одного игрока равен проигрышу второго, а следовательно цели этих игроков прямо противоположны. Такая игра описывается платежной матрицей, в которой задаются выигрыши первого игрока. Номер строки матрицы соответствует номеру применяемой стратегии первого игрока, столбец - номеру применяемой стратегии второго игрока.

Величина β называется верхней ценой игры или минимаксным проигрышем. Это гарантированный проигрыш игрока B Величина β называется верхней ценой игры или минимаксным проигрышем. Это гарантированный проигрыш игрока B при любой стратегии игрока А. Из каждого столбца выбираем максимальное число, а затем из всех максимумов берем минимум.

Величина α называется нижней ценой игры или максиминным выигрышем. Это гарантированный выигрыш игрока А Величина α называется нижней ценой игры или максиминным выигрышем. Это гарантированный выигрыш игрока А при любой стратегии игрока В. Из каждой строки выбираем минимальное число, а затем из всех этих минимумов выбираем максимум.

То игру называют, игрой с седловой точкой. Седловая точка минимальная в своей строке и То игру называют, игрой с седловой точкой. Седловая точка минимальная в своей строке и максимальная в своём столбце.

Основная теорема теории игр (теорема фон Неймана). Любая матричная игра имеет решение, то есть Основная теорема теории игр (теорема фон Неймана). Любая матричная игра имеет решение, то есть существуют оптимальные стратегии и цена игры. Джон фон Нейман 28 декабря 1903, Будапешт-8 февраля 1957, Вашингтон. Сделал важный вклад в квантовую физику, квантовую логику, функциональный анализ, теорию множеств, теорию автоматов, кибернетику, информатику, экономику и другие отрасли науки. Важную роль в экономике сыграла теория игр, разработанная Нейманом и О. Моргенштерном “Теория игр и экономическое поведение” в 1944 г.

Для того, чтобы найти решение матричной игры, необходимо следовать следующему алгоритму: 1. Проверяем, имеет Для того, чтобы найти решение матричной игры, необходимо следовать следующему алгоритму: 1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях, если нет продолжаем анализ матрицы. 2. Удаляем, если они есть, доминируемые строки и доминирующие столбцы.

Строка платежной матрицы называется доминируемой строкой, если все ее элементы не больше соответствующих элементов Строка платежной матрицы называется доминируемой строкой, если все ее элементы не больше соответствующих элементов какой-либо другой строки. Столбец называется доминирующим столбцом, если все его элементы не меньше соответствующих элементов какоголибо другого столбца. Доминируемые строки и доминирующие столбцы удаляем из платежной матрицы, и на их месте в оптимальных стратегиях игроков ставим нули.

3. Решаем матричную игру одним из известных методов: методами линейного программирования, приближенным методом или 3. Решаем матричную игру одним из известных методов: методами линейного программирования, приближенным методом или графически (если хотя бы у одного из игроков есть только две чистые стратегии). Решение игры методом линейного программирования. Задача линейного программирования состоит из трёх частей: q системы ограничений, которая состоит из m линейных уравнений и неравенств с n неизвестными; q условия неотрицательности переменных, вытекает из экономического смысла вводимых переменных; q целевой функции. При решении игры методом линейного

Решение задачи ЛП заключается в нахождении оптимального плана Х* и вычислении значения целевой функции Решение задачи ЛП заключается в нахождении оптимального плана Х* и вычислении значения целевой функции на этом плане . При решении игры методом линейного программирования приводим матричную игру к паре симметричных двойственных задач. Если в платёжной матрице есть отрицательные числа, прибавляем ко всем элементам одно и тоже положительное число, чтобы в новой матрице все элементы были неотрицательны.

Исходная задача будет стандартной задачей максимизации, матрица коэффициентов этой задачи совпадут с преобразованной платежной Исходная задача будет стандартной задачей максимизации, матрица коэффициентов этой задачи совпадут с преобразованной платежной матрицей , а коэффициенты при неизвестных в целевой функции и свободные члены неравенств будут равны единице. Найти решение игры, заданной платежной матрицей:

В матрице нет седловой точки: следовательно, игра имеет решение в смешанных стратегиях. Проверим, есть В матрице нет седловой точки: следовательно, игра имеет решение в смешанных стратегиях. Проверим, есть ли в матрице доминируемые строки и доминирующие столбцы. Все элементы первой строки не больше соответствующих элементов третьей строки, поэтому первая строка является доминируемой и ее можно удалить. Также можно удалить третий столбец, он доминирует над вторым, а также пятый столбец, доминирующий над первыми тремя столбцами.

В результате получим матрицу: Прибавив ко всем элементам матрицы А', число с = 3, В результате получим матрицу: Прибавив ко всем элементам матрицы А', число с = 3, получим матрицу:

Составим пару симметричных двойственных задач. Исходная задача будет стандартной задачей максимизации, матрица коэффициентов этой Составим пару симметричных двойственных задач. Исходная задача будет стандартной задачей максимизации, матрица коэффициентов этой задачи совпадёт с платежной матрицей А", коэффициенты при неизвестных в целевой функции и свободные члeны неравенств будут равны единице. Вторая задача будет стандартной задачей минимизации. Матрицу коэффициентов этой задачи получим транспонировав платежную матрицу А",

Решим задачу 1 симплекс-методом. Алгоритм решения задачи симплекс – методом. I шаг. Составление начального Решим задачу 1 симплекс-методом. Алгоритм решения задачи симплекс – методом. I шаг. Составление начального базисного плана. Задача ЛП должна быть задана в канонической форме. Т. е. система ограничений должна состоять только из уравнений, правые части которых неотрицательны. Для этого в левую часть каждого неравенства вводят дополнительную неотрицательную переменную: со знаком «+» .

В каждом уравнении должна быть базисная переменная. Базисная переменная -это переменная с коэффициентом +1, В каждом уравнении должна быть базисная переменная. Базисная переменная -это переменная с коэффициентом +1, содержится только в одном уравнении и отсутствует во всех остальных. Целевая функция - максимизируется. Составим начальный базисный план для задачи 1. Задача задана в общей форме. Приведём её к канонической добавив дополнительные неизвестные x 4≥ 0, x 5≥ 0. В результате получим следующую задачу:

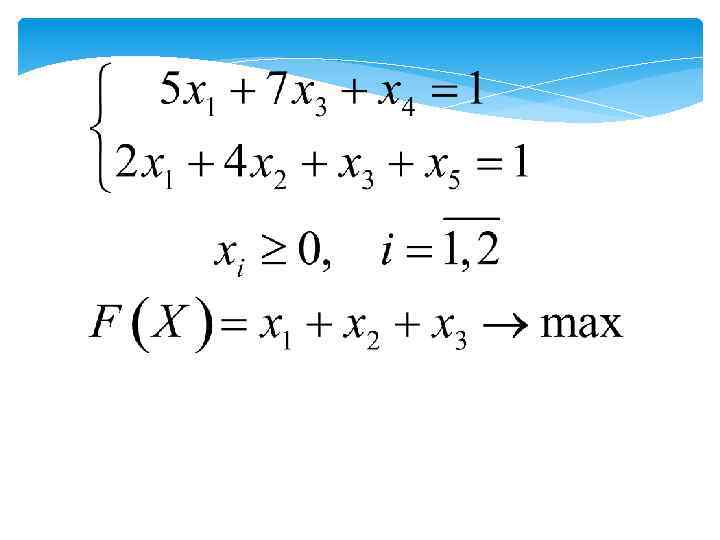
Далее составляется симплекс-таблица. Каждая строка симплекс-таблицы соответствует уравнению системы ограничений. В первый столбец выписывается Далее составляется симплекс-таблица. Каждая строка симплекс-таблицы соответствует уравнению системы ограничений. В первый столбец выписывается название переменной, которая является базисной для данного уравнения. Во второй столбец записываются свободные члены уравнений, остальные элементы таблицы равны коэффициентам при соответствующих неизвестных.

Базис- Свобоная дные перечлены менная Х 1 Х 2 Х 3 Х 4 Х Базис- Свобоная дные перечлены менная Х 1 Х 2 Х 3 Х 4 Х 5 Х 4 1 5 0 7 1 0 Х 5 1 2 4 1 0 1 F В последнюю строку таблицы записывают целевую функцию F(Х), эта строка называется индексной.

Элементы индексной строки заполняются по следующему правилу. Слева от симплекс-таблицы выписываются коэффициенты при базисных Элементы индексной строки заполняются по следующему правилу. Слева от симплекс-таблицы выписываются коэффициенты при базисных переменных целевой функции, над верхней строкой симплекс-таблицы выписываются коэффициенты при соответствующих переменных целевой функции. Далее коэффициенты , (слева от таблицы) умножим на элементы соответствующего столбца и полученные произведения складываются. Затем из полученной суммы вычитается коэффициент сверху таблицы (для столбца свободных членов коэффициент сверху прибавляется).

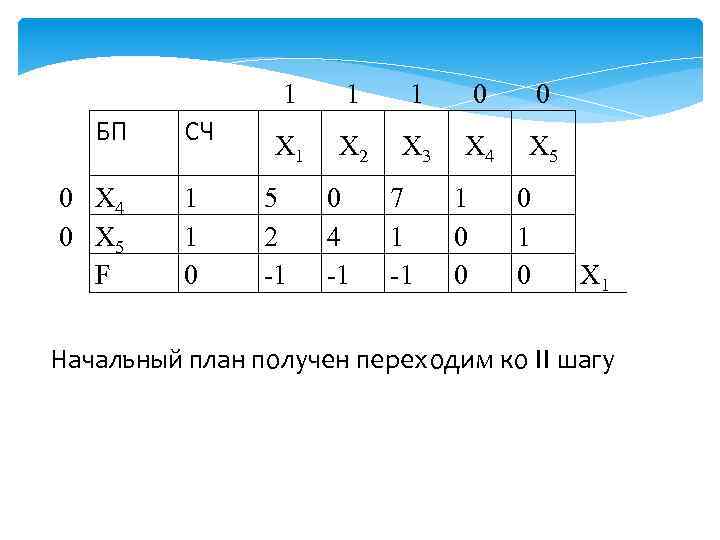БП 0 Х 4 0 Х 5 F СЧ 1 1 0 1 БП 0 Х 4 0 Х 5 F СЧ 1 1 0 1 1 1 0 0 Х 1 Х 2 Х 3 Х 4 Х 5 5 2 -1 0 4 -1 7 1 -1 1 0 0 0 1 0 Х 1 Начальный план получен переходим ко II шагу

II шаг. Проверка плана на оптимальность заключается в анализе коэффициентов индексной строки (кроме столбца II шаг. Проверка плана на оптимальность заключается в анализе коэффициентов индексной строки (кроме столбца свободных членов ). Если среди элементов индексной строки есть отрицательные, то это означает, что целевая функция не достигла максимального значения и план может быть улучшен. Переходим к III шагу.

III шаг. Построение нового плана. 1. Среди отрицательных элементов индексной строки выбираем наибольший по III шаг. Построение нового плана. 1. Среди отрицательных элементов индексной строки выбираем наибольший по абсолютной величине (если таких несколько, можно взять любой из них). Соответствующий ему столбец называется ключевым столбцом, выделяем его. Переменная, соответствующая ключевому столбцу, войдет в новый базисный план.

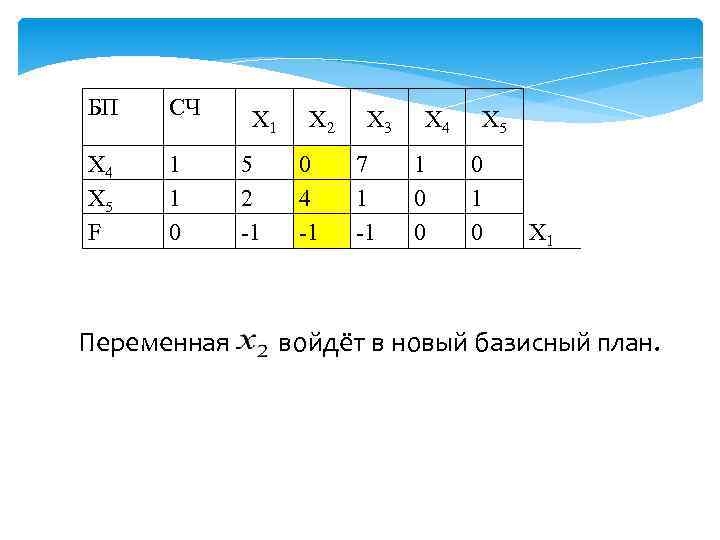БП СЧ Х 4 Х 5 F 1 1 0 Переменная Х 1 5 БП СЧ Х 4 Х 5 F 1 1 0 Переменная Х 1 5 2 -1 Х 2 0 4 -1 Х 3 7 1 -1 Х 4 1 0 0 Х 5 0 1 0 Х 1 войдёт в новый базисный план.

2. Среди элементов ключевого столбца находим ключевой элемент. Для этого составляем отношения свободных членов 2. Среди элементов ключевого столбца находим ключевой элемент. Для этого составляем отношения свободных членов к положительным элементам ключевого столбца; среди всех отношений выбираем минимальное. Знаменатель этого минимального отношения принимаем за ключевой элемент. Содержащая ключевой элемент строка соответствует переменной, которая выводится из базиса.

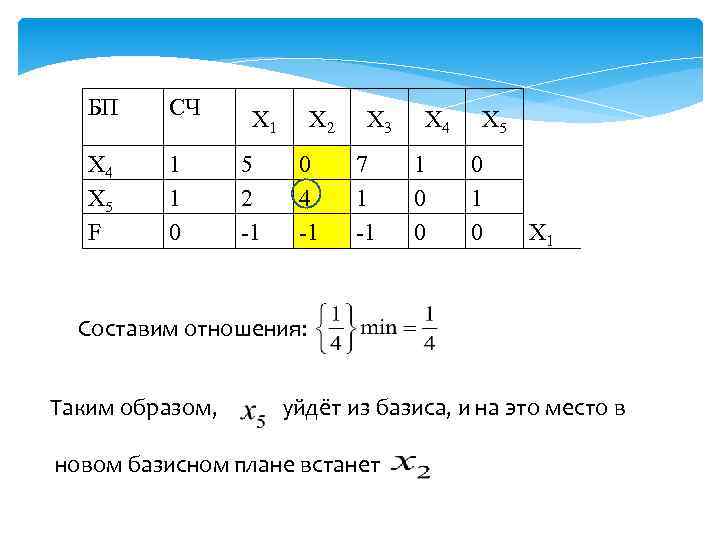БП СЧ Х 4 Х 5 F 1 1 0 Х 1 5 2 БП СЧ Х 4 Х 5 F 1 1 0 Х 1 5 2 -1 Х 2 0 4 -1 Х 3 7 1 -1 Х 4 1 0 0 Х 5 0 1 0 Х 1 Составим отношения: Таким образом, уйдёт из базиса, и на это место в новом базисном плане встанет

3. Все элементы строки, в которой находится ключевой элемент, делятся на значение ключевого элемента. 3. Все элементы строки, в которой находится ключевой элемент, делятся на значение ключевого элемента. Полученная строка называется ключевой строкой и записывается в новую таблицу на соответствующее место. Ключевую строку выделяем.

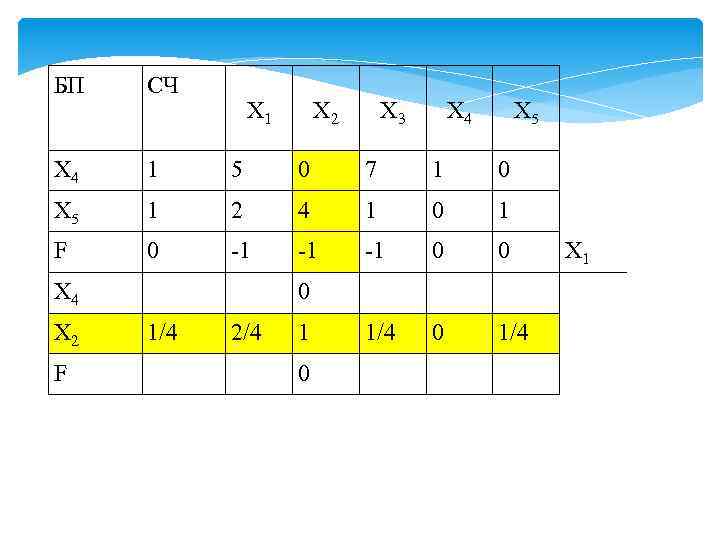БП СЧ Х 4 1 5 0 7 1 0 Х 5 1 2 БП СЧ Х 4 1 5 0 7 1 0 Х 5 1 2 4 1 0 1 F 0 -1 -1 -1 0 0 Х 1 Х 4 0 Х 2 1/4 2/4 1 1/4 0 1/4 F 0 Х 1 Х 2 Х 3 Х 4 Х 5

4. Остальные элементы новой таблицы (включая элементы индексной строки) находятся по правилу двух перпендикуляров. 4. Остальные элементы новой таблицы (включая элементы индексной строки) находятся по правилу двух перпендикуляров. : «прежнее значение элемента минус произведение чисел, стоящих на концах перпендикуляров, опущенных из этого элемента на ключевой столбец и ключевую строку» . Заполнение новой таблицы рациональнее начинать с индексной строки, так как если все ее элементы окажутся неотрицательными, то план оптимален, и для остальных переменных достаточно будет вычислить лишь значения столбца свободных членов.

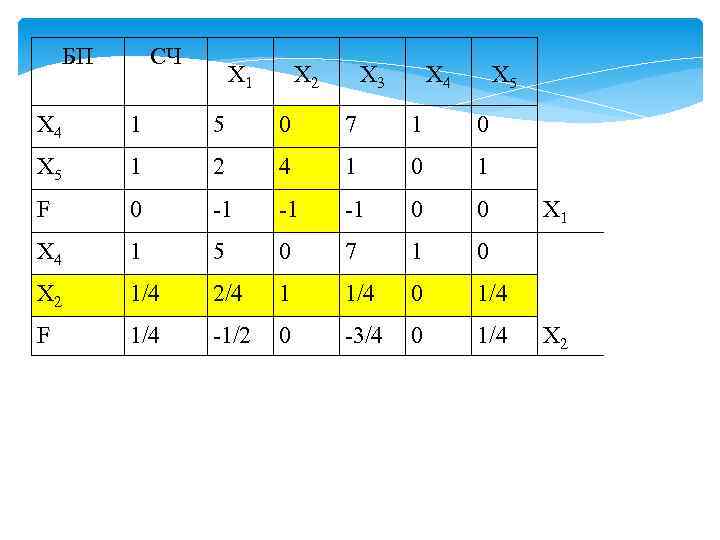БП СЧ Х 1 Х 2 Х 3 Х 4 Х 5 Х 4 БП СЧ Х 1 Х 2 Х 3 Х 4 Х 5 Х 4 1 5 0 7 1 0 Х 5 1 2 4 1 0 1 F 0 -1 -1 -1 0 0 Х 1 Х 4 1 5 0 7 1 0 Х 2 1/4 2/4 1 1/4 0 1/4 F 1/4 -1/2 0 -3/4 0 1/4 Х 2

План не оптимален, в индексной строке есть отрицательные числа. Построим новый план. Среди отрицательных План не оптимален, в индексной строке есть отрицательные числа. Построим новый план. Среди отрицательных элементов индексной строки выбираем наибольший по абсолютной величине. Это: Соответствующий столбец будет ключевым столбцом, выделяем его. Переменная соответствующая ключевому столбцу, войдет в новый базисный план. . Среди элементов ключевого столбца находим ключевой элемент.

Для этого составляем отношения свободных членов к положительным элементам ключевого столбца; среди всех отношений Для этого составляем отношения свободных членов к положительным элементам ключевого столбца; среди всех отношений выбираем минимальное. Знаменатель этого минимального отношения принимаем за ключевой элемент. Содержащая ключевой элемент строка соответствует переменной , которая выводится из базиса. Составим новый базисный план.

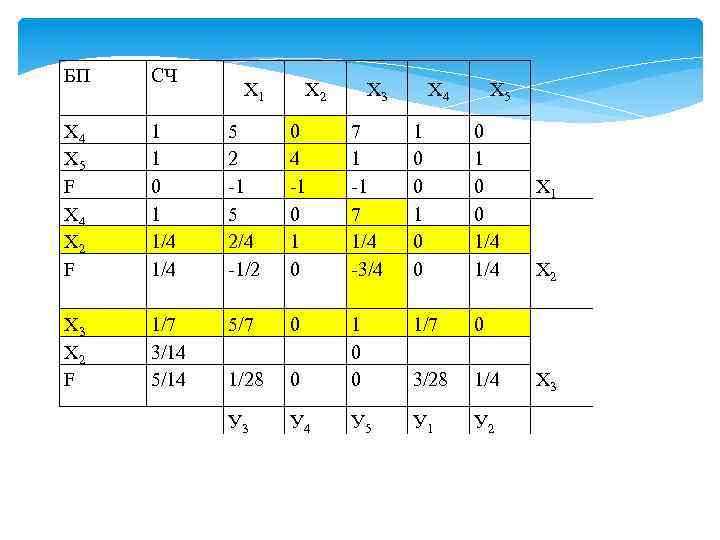БП Х 4 Х 5 F Х 4 Х 2 F СЧ 1 1 БП Х 4 Х 5 F Х 4 Х 2 F СЧ 1 1 0 1 1/4 5 2 -1 5 2/4 -1/2 0 4 -1 0 7 1 -1 7 1/4 -3/4 1 0 0 0 1/4 Х 3 Х 2 F 1/7 3/14 5/7 1/28 0 0 1 0 0 1/7 3/28 0 1/4 У 3 У 4 У 5 У 1 У 2 Х 1 Х 2 Х 3 Х 4 Х 5 Х 1 Х 2 Х 3

По свойствам двойственных задач установим соответствие между основными переменными прямой задачи и дополнительными переменными По свойствам двойственных задач установим соответствие между основными переменными прямой задачи и дополнительными переменными двойственной Для того, чтобы составить соответствие в нашем случае преобразуем задачу 2, записав вместо неравенств уравнения.

Из столбца свободных членов и индексной строки симплекс таблицы выпишем оптимальные планы пары двойственных Из столбца свободных членов и индексной строки симплекс таблицы выпишем оптимальные планы пары двойственных задач. Получим: