Матричний метод Мюллера Деполяризуючи властивості середовища деполяризаційні

Матричний метод Мюллера

Деполяризуючи властивості середовища: деполяризаційні метрики

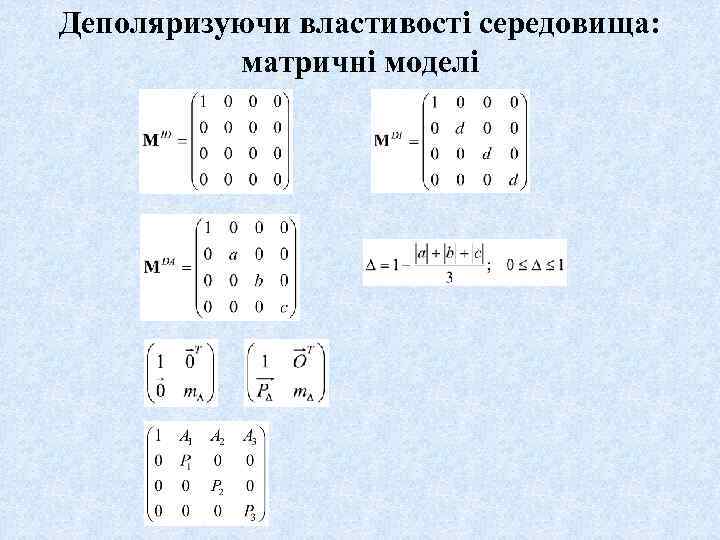Деполяризуючи властивості середовища: матричні моделі

Теореми еквівалентності Джонса Перша теорема i (Δ 1, 1) 1 (Δj, j) (Δ , ) Друга теорема 1 (P 1, 1) (P i, i) j (P , ) Третя теорема (Δ 1, 1) 1 (P 1, 1) (R 1) (Δj, j) (P i, i) (Δ 1, 1) (Δ 2, 2) k (Rl) (P , 0)

Теореми еквівалентності Джонса 1. 2.

Теореми еквівалентності Джонса

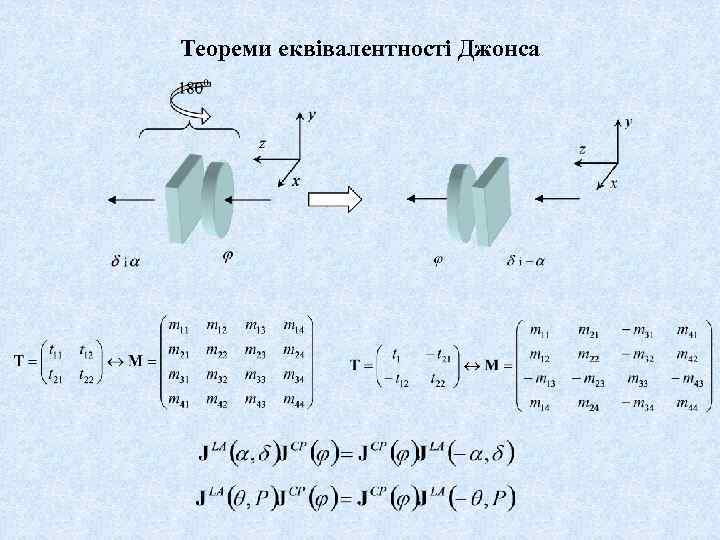Теореми еквівалентності Джонса Третя теорема (Δ 1, 1) 1 (P 1, 1) (R 1) (Δj, j) (P i, i) (Δ 1, 1) (Δ 2, 2) k (Rl) (P , 0)

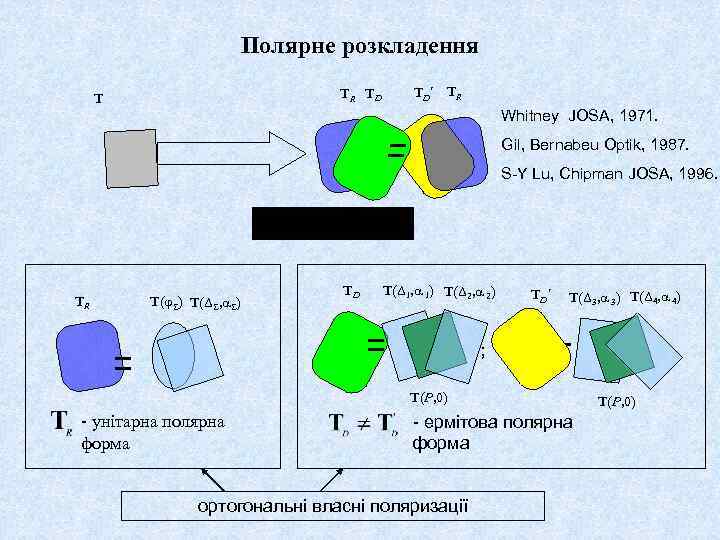Полярне розкладення TR TD T TD´ TR Whitney JOSA, 1971. Gil, Bernabeu Optik, 1987. S-Y Lu, Chipman JOSA, 1996. TR T( ) T(Δ , ) TD T(Δ 1, 1) T(Δ 2, 2) TD´ T(Δ 3, 3) T(Δ 4, 4) ; T(P, 0) - унітарна полярна форма - ермітова полярна форма ортогональні власні поляризації T(P, 0)

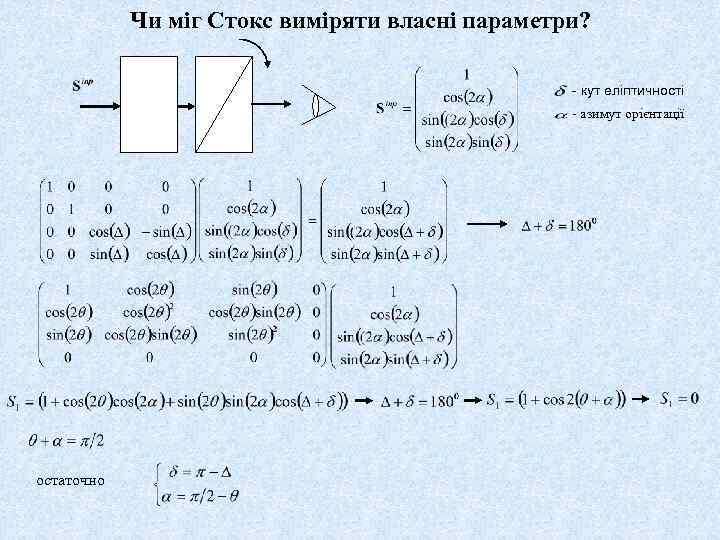Чи міг Стокс виміряти власні параметри? - кут еліптичності - азимут орієнтації остаточно

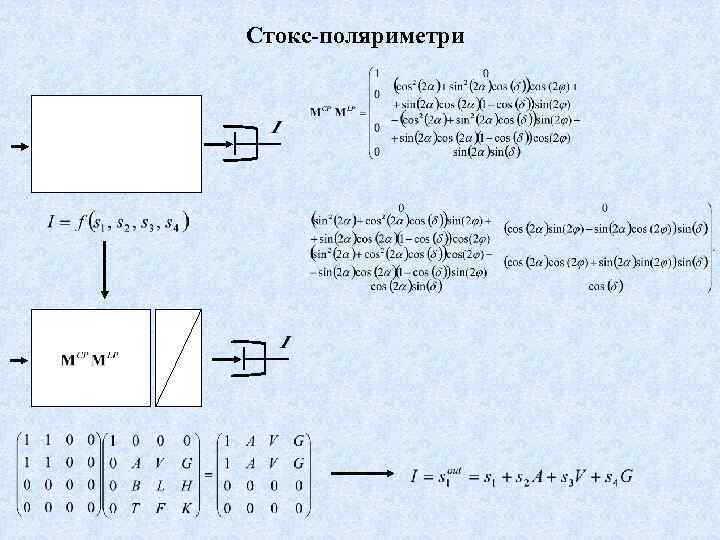Стокс-поляриметри