Maths Revision Grade C D topics and

Maths Revision Grade C & D topics and exam questions

Percentage Increase or Decrease = Difference Original X 100 Question: A club increases their membership fee from £ 12 to £ 15 per year. What is the percentage increase? Answer 15 -12 x 100 = 3 x 100 = 12 12 4 25%

Questions on Percentage Increase or Decrease 1. In a sale the price of a computer is reduced from £ 500 to £ 379. What is the percentage decrease? 2. Jane earns £ 11400 per year. After a year her pay rise she earns £ 12198 per year. What was her percentage pay rise? 3. The house price index for a flat in Leeds was 190 in August 2006, compared with a base of 100 in April 2000. a) Write down the percentage increase in the price of flat in Leeds in that period. b) A flat cost £ 80000 in April 2000. What was its likely value in August 2006?

Averages 4 6 3 9 7 10 6 Mode : The value which occurs most common. 4 6 3 9 7 10 6 = 6 Range : Highest value minus the lowest value. 4 6 3 9 7 10 6 = 10 – 3 = 7 Median : The middle value when data is in order (low –high). 3 4 6 6 7 9 10 = 6 Mean : Numbers added together, divided by the number of items. 4 + 6 + 3 + 9 + 7 + 10 + 6 = 45 / 7 = 6. 4

Questions on Averages Mrs Wilson givers her class a test, here are their marks out of 20: 17 14 16 13 9 10 17 18 16 8 17 1. Work out the Mode? 2. Work out the Median? 3. Write down the Range? 4. Mrs Wilson tells her class that the pass mark is 75% How many students pass the test?

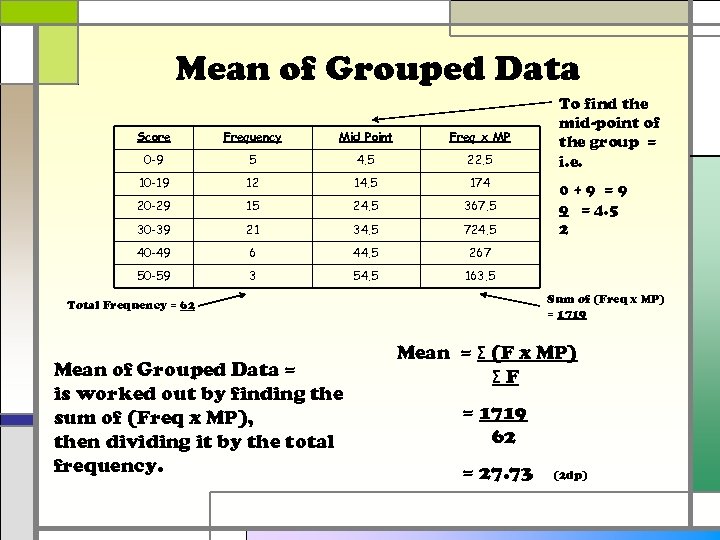Mean of Grouped Data Score Frequency Mid Point Freq x MP 0 -9 5 4. 5 22. 5 10 -19 12 14. 5 174 20 -29 15 24. 5 367. 5 30 -39 21 34. 5 724. 5 40 -49 6 44. 5 267 50 -59 3 54. 5 To find the mid-point of the group = i. e. 163. 5 Sum of (Freq x MP) = 1719 Total Frequency = 62 Mean of Grouped Data = is worked out by finding the sum of (Freq x MP), then dividing it by the total frequency. 0+9 =9 9 = 4. 5 2 Mean = Σ (F x MP) ΣF = 1719 62 = 27. 73 (2 dp)

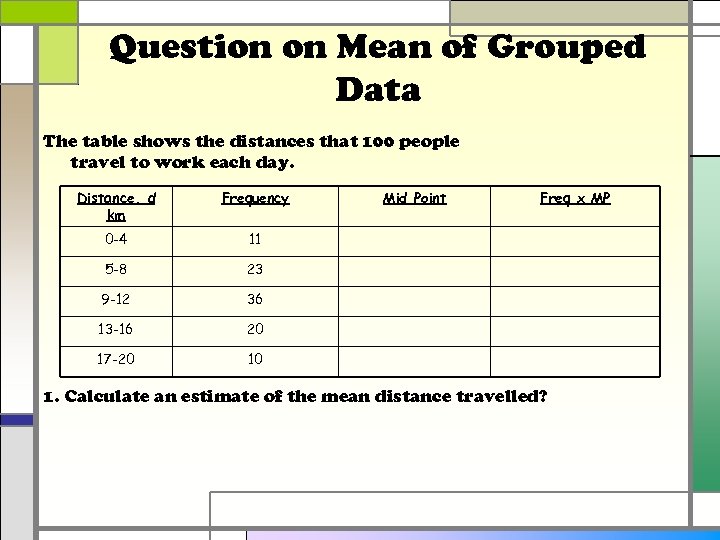Question on Mean of Grouped Data The table shows the distances that 100 people travel to work each day. Distance, d km Frequency 0 -4 11 5 -8 23 9 -12 36 13 -16 20 17 -20 Mid Point Freq x MP 10 1. Calculate an estimate of the mean distance travelled?

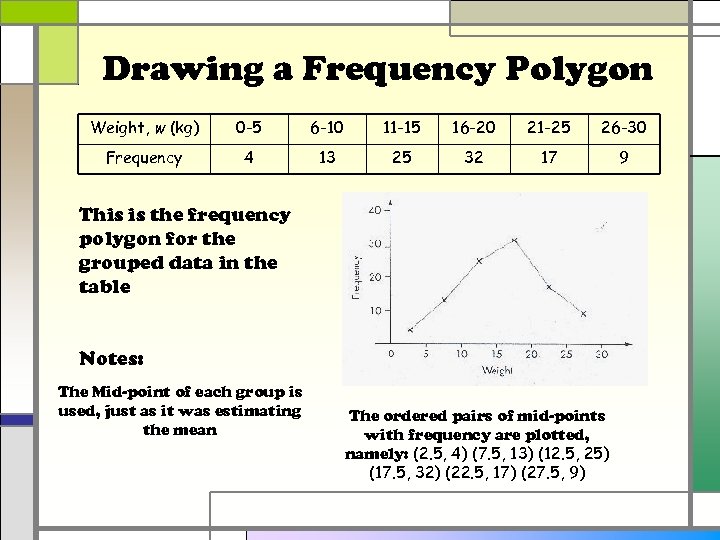Drawing a Frequency Polygon Weight, w (kg) 0 -5 6 -10 11 -15 16 -20 21 -25 26 -30 Frequency 4 13 25 32 17 9 This is the frequency polygon for the grouped data in the table Notes: The Mid-point of each group is used, just as it was estimating the mean The ordered pairs of mid-points with frequency are plotted, namely: (2. 5, 4) (7. 5, 13) (12. 5, 25) (17. 5, 32) (22. 5, 17) (27. 5, 9)

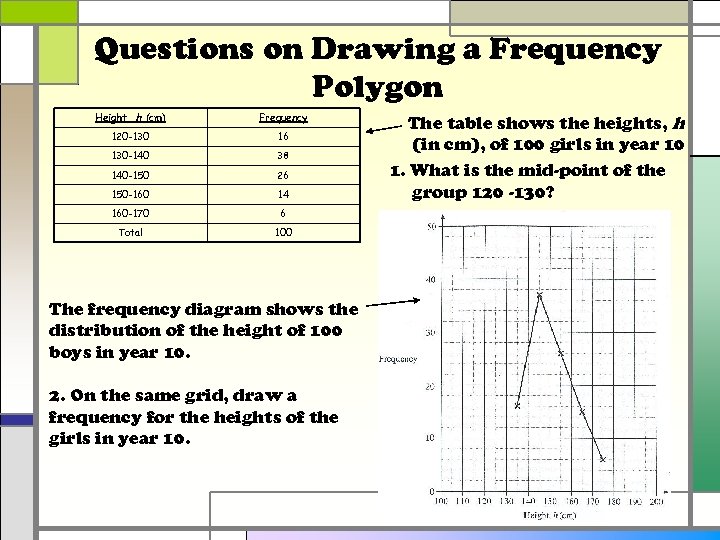Questions on Drawing a Frequency Polygon Height, h (cm) Frequency 120 -130 16 130 -140 38 140 -150 26 150 -160 14 160 -170 6 Total 100 The frequency diagram shows the distribution of the height of 100 boys in year 10. 2. On the same grid, draw a frequency for the heights of the girls in year 10. The table shows the heights, h (in cm), of 100 girls in year 10 1. What is the mid-point of the group 120 -130?

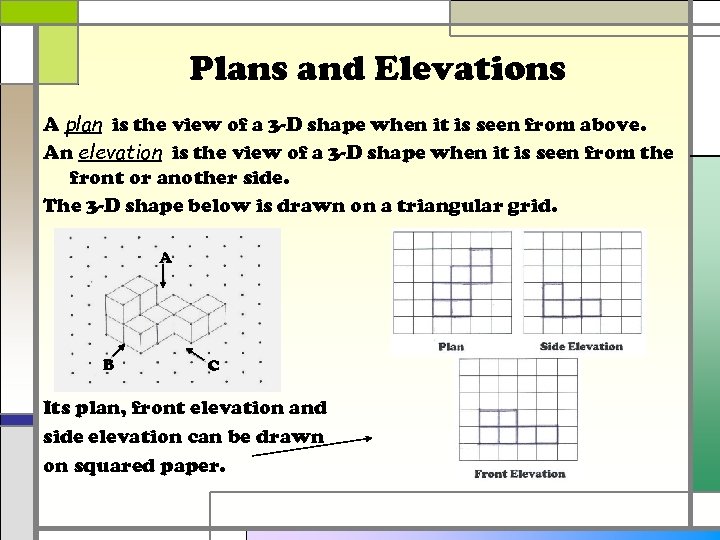Plans and Elevations A plan is the view of a 3 -D shape when it is seen from above. An elevation is the view of a 3 -D shape when it is seen from the front or another side. The 3 -D shape below is drawn on a triangular grid. A B C Its plan, front elevation and side elevation can be drawn on squared paper.

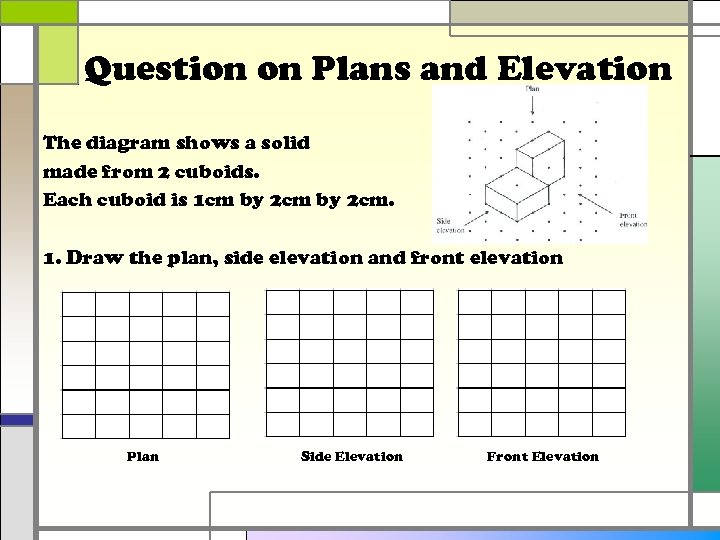Question on Plans and Elevation The diagram shows a solid made from 2 cuboids. Each cuboid is 1 cm by 2 cm. 1. Draw the plan, side elevation and front elevation Plan Side Elevation Front Elevation

Ratios + ÷ × Compare 2 or more quantities. e. g. 1. Ratio of Boys to Girls 2: 3 (for every 2 boys there are 3 girls) 2. Divide £ 500 into the ratio a) the ratio has 1 + 2 + 7 parts = 10 parts So 1 part = 500 10 = 50 1: 2: 7 1 × 50 2 × 50 7 × 50 = 100 = 350 50 100 +350 500 (Check your working)

Questions on Ratio 1. Adam is aged 12 Brenda is aged 8 They share £ 170 between them in the ration of their ages How much does each receive? 2. Leah, Chloe and Maya share £ 400 between them. Leah receives the smallest amount of £ 90 The ratio of Leah’s share to Chloe’s share is 2: 3 Work out how much Maya receives?

Trial and Improvement A method of ‘Guessing’ and answer! *An equation has a solution which can’t be solved by another method. *Refine your guess until you get as close as you can Example: Guess x 3 + 5 x = 70 Answer Result x=3 33 + 5 x 3 = 42 Too small x=4 43 + 5 x 4 = 84 Too big x = 3. 63 + 5 x 3. 6 = 64. 656 Too small x = 3. 73 + 5 x 3. 7 = 69. 153 Too small x = 3. 753 + 5 x 3. 75 = 71. 484375 Too Big X = 3. 7 (1 d. p. )

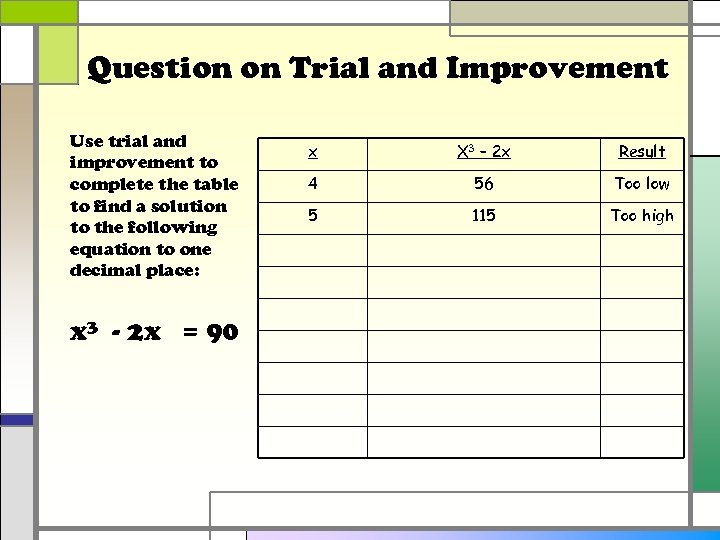Question on Trial and Improvement Use trial and improvement to complete the table to find a solution to the following equation to one decimal place: x 3 - 2 x = 90 x X 3 – 2 x Result 4 56 Too low 5 115 Too high

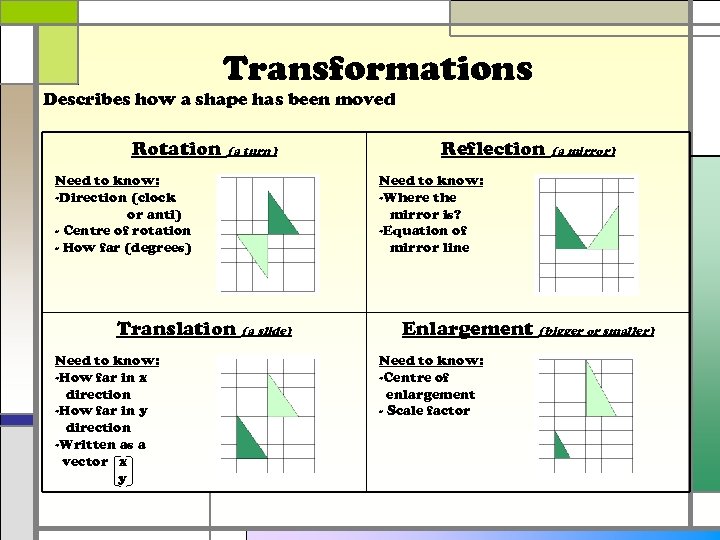Transformations Describes how a shape has been moved Rotation (a turn) Need to know: -Direction (clock or anti) - Centre of rotation - How far (degrees) Translation (a slide) Need to know: -How far in x direction -How far in y direction -Written as a vector x y Reflection (a mirror) Need to know: -Where the mirror is? -Equation of mirror line Enlargement (bigger or smaller) Need to know: -Centre of enlargement - Scale factor

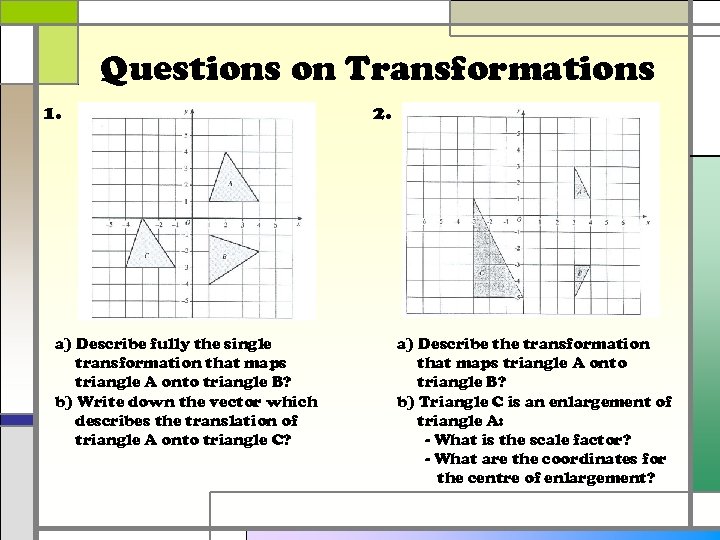Questions on Transformations 1. a) Describe fully the single transformation that maps triangle A onto triangle B? b) Write down the vector which describes the translation of triangle A onto triangle C? 2. a) Describe the transformation that maps triangle A onto triangle B? b) Triangle C is an enlargement of triangle A: - What is the scale factor? - What are the coordinates for the centre of enlargement?

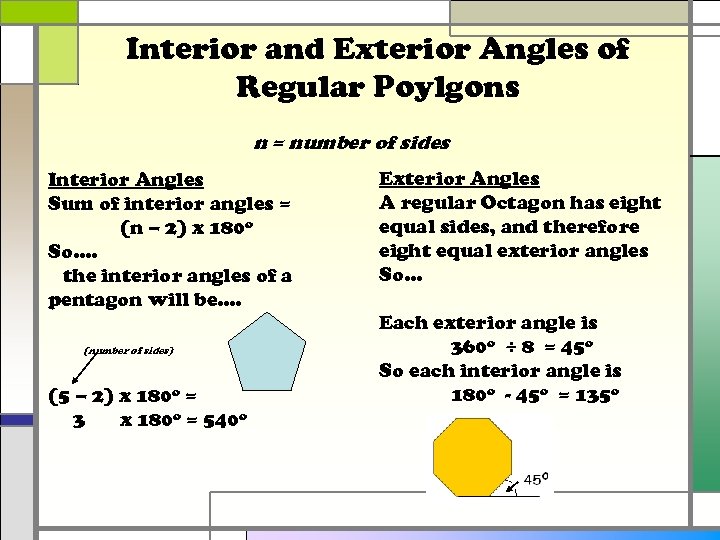Interior and Exterior Angles of Regular Poylgons n = number of sides Interior Angles Sum of interior angles = (n – 2) x 180 o So…. the interior angles of a pentagon will be…. (number of sides) (5 – 2) x 180 o = 3 x 180 o = 540 o Exterior Angles A regular Octagon has eight equal sides, and therefore eight equal exterior angles So… Each exterior angle is 360 o ÷ 8 = 45 o So each interior angle is 180 o - 45 o = 135 o

Questions on Interior and Exterior Angles of Regular Polygons 1. The diagram shows part of a regular polygon: a. Calculate the size of the exterior angle of the polygon? b. Calculate the number of sides of the polygon? 2. ABCDE is a regular Pentagon DEF and BAF are straight lines: a. Work out the size of the angle marked x on the diagram? b. Work out the size of the angle marked y on the diagram?

Pythagoras Side length calculation in Right Angled Triangles. Side Length C must always be the HYPOTENUSE - Label the triangle. - Put values into formula. - Square each number. - Rearrange for x = - (Square Root) Example: a 2 + b 2 = c 2 x 2 + 122 = 152 x 2 + 144 = 225 x = √ 225 - 144 x = √ 81 x = 9 cm

Questions for Pythagoras 1. Calculate the length of the side marked x? 2. Calculate the length of the side marked x? 3. Calculate the length of the side marked x?

Finding the nth term of a linear sequence. The nth term of a linear sequence is always of the form An + b A = is the difference between each term and the next term. b = is the difference between the first term and A. Example: Find the nth term of the sequence 5, 7, 9, 11, 13…. . The difference between terms is 2, so the first part = 2 n. Subtract the difference, 2, from the first term, 5: =5 -2 = 3. So the nth term is given by 2 n + 3 Example 2: From the sequence 5, 12, 19 26, 33…… find a) the nth term b) the 50 th term. a) The difference between terms is 7, so first part is 7 n. Subtract the difference 7, from first term, 5: 5 -7 = -2 So the nth term is found by giving 7 n – 2. b) The 50 th term is given by substituting n = 50 into the rule, 7 n -2. 50 th term = 7 x 50 - 2 = 348

Questions on Finding the nth term of a linear sequence. 1. Work out the nth term in the sequence: 5, 11, 17, 23, 29, ………………. . 2. Work out the nth term in the sequence: 2, 5, 8, 11, 14, ………………. . 3. Work out the nth term in the sequence: 5, 7, 9, 11, 13, ………………. .

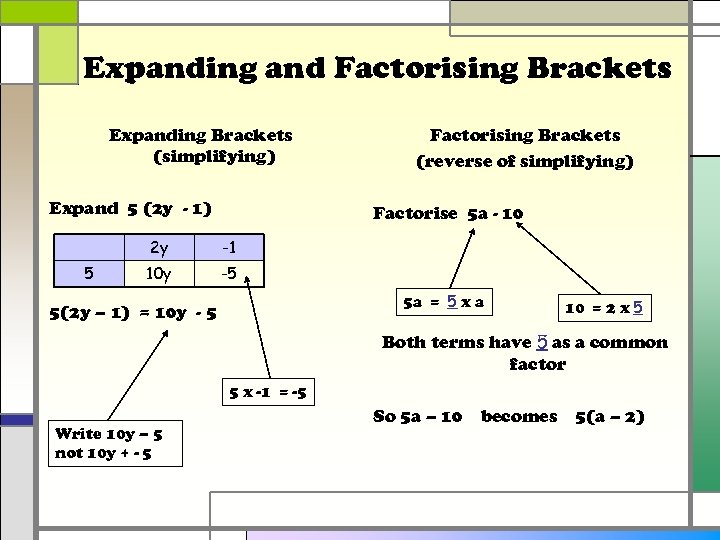Expanding and Factorising Brackets Expanding Brackets (simplifying) Expand 5 (2 y - 1) Factorise 5 a - 10 2 y 5 Factorising Brackets (reverse of simplifying) -1 10 y -5 5 a = 5 x a 5(2 y – 1) = 10 y - 5 10 = 2 x 5 Both terms have 5 as a common factor 5 x -1 = -5 Write 10 y – 5 not 10 y + - 5 So 5 a – 10 becomes 5(a – 2)

Questions on Expanding and Factorising Brackets 1. Expand 2 x (x – 4) and d (d 2 + 6) 2. Simplify g 4 + g 4 and w 6 x w 3 3. Factorise y 2 – 5 y 4. Expand Simplify 2(x – 4) + 3(2 x + 5) 5. Expand Simplify 2(p + 5) + 3(2 p – 1)

The 4 Inequality Symbols ‹ means ‘greater than’ ≤ means ‘greater than or equal to’ › means ‘less than’ ≥ means ‘less than or equal to’ Example 1: Solve the inequality 5 x + 2 ≤ 17 Answer: 5 x + 2 ≤ -2 5 x ÷ 5 x ≤ ≤ Example 2: Write down all the integer values satisfying this inequality: -6 17 -2 15 ÷ 5 3 ≤ 3 x Answer: -6 ÷ 3 -2 ≤ ≤ 3 x ÷ 3 3 x ‹ ‹ ‹ 9 9 ÷ 3 3 So integer values that satisfy the inequality are -2, -1, 0, 1, 2, 3

Questions on The 4 Inequality Symbols 1. Solve the inequality 3 x + 2 ≤ 8 2. Solve the inequality 3 x + 1 ≥ 7 3. Solve the equation 5 z + 13 = 2(z – 1) 4. Write down all the integer values of x satisfying this inequality -4 ≤ 2 x ‹ 4

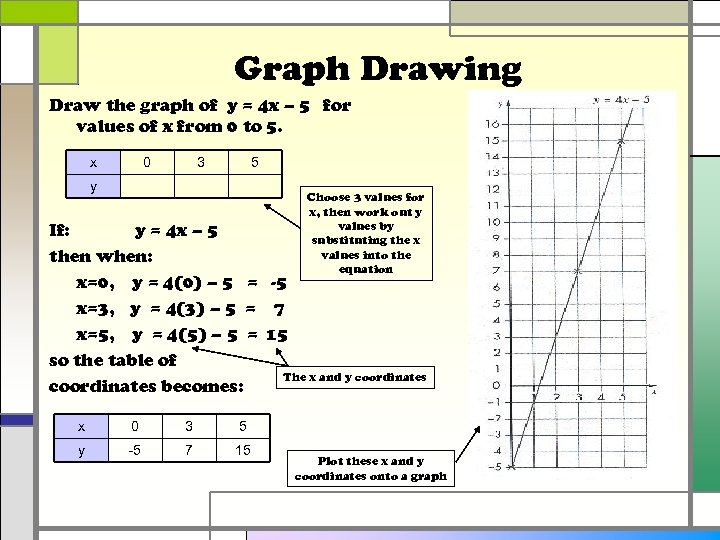Graph Drawing Draw the graph of y = 4 x – 5 for values of x from 0 to 5. x 0 3 5 y Choose 3 values for x, then work out y values by substituting the x values into the equation If: y = 4 x – 5 then when: x=0, y = 4(0) – 5 = -5 x=3, y = 4(3) – 5 = 7 x=5, y = 4(5) – 5 = 15 so the table of The x and y coordinates becomes: x 0 3 5 y -5 7 15 Plot these x and y coordinates onto a graph

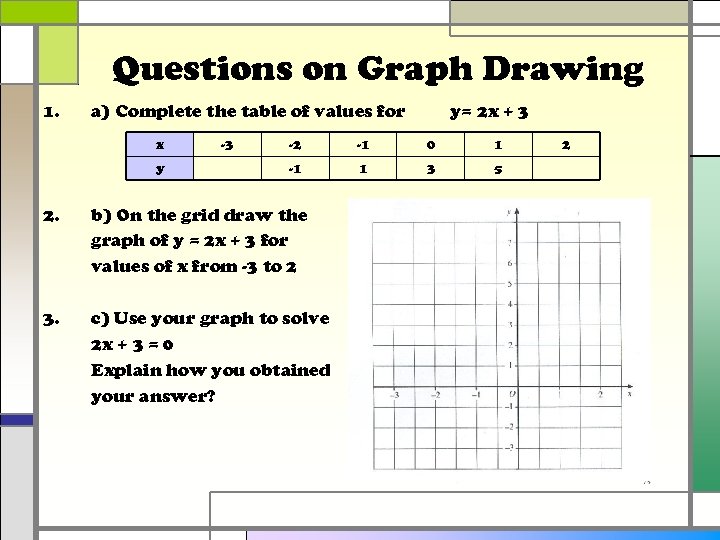Questions on Graph Drawing 1. a) Complete the table of values for x y -3 y= 2 x + 3 -2 -1 0 1 -1 1 3 5 2. b) On the grid draw the graph of y = 2 x + 3 for values of x from -3 to 2 3. c) Use your graph to solve 2 x + 3 = 0 Explain how you obtained your answer? 2

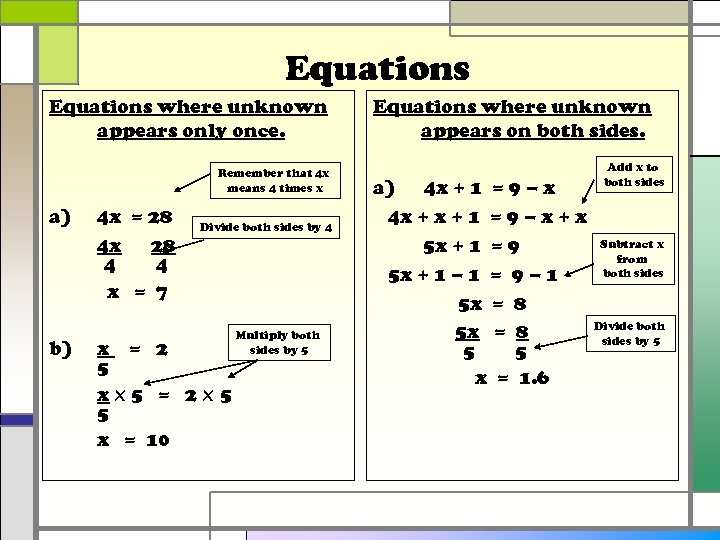Equations where unknown appears only once. Remember that 4 x means 4 times x a) b) 4 x = 28 4 x 28 4 4 x = 7 Divide both sides by 4 x = 2 5 xx 5 = 2 x 5 5 x = 10 Multiply both sides by 5 Equations where unknown appears on both sides. a) 4 x + 1 = 9 – x + x 5 x + 1 = 9 5 x + 1 – 1 = 9 – 1 5 x = 8 5 5 x = 1. 6 Add x to both sides Subtract x from both sides Divide both sides by 5

Questions on Equations 1. Solve the following equations: a) 7 x – 9 = 3 x +5 b) 7(y – 9) = 3 y + 5 c) 7 x = 28 d) x 5 = 10 2. You are given that 6 y = 48, 3. Find the value of 3 x + 5 y when x = 7 and y = -4? work out the value of 5 y?

ANSWERS

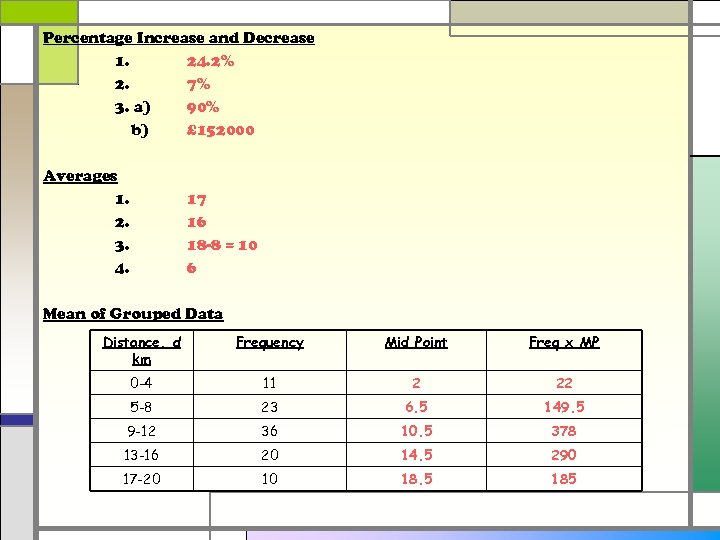Percentage Increase and Decrease 1. 24. 2% 2. 7% 3. a) 90% b) £ 152000 Averages 1. 2. 3. 4. 17 16 18 -8 = 10 6 Mean of Grouped Data Distance, d km Frequency Mid Point Freq x MP 0 -4 11 2 22 5 -8 23 6. 5 149. 5 9 -12 36 10. 5 378 13 -16 20 14. 5 290 17 -20 10 18. 5 185

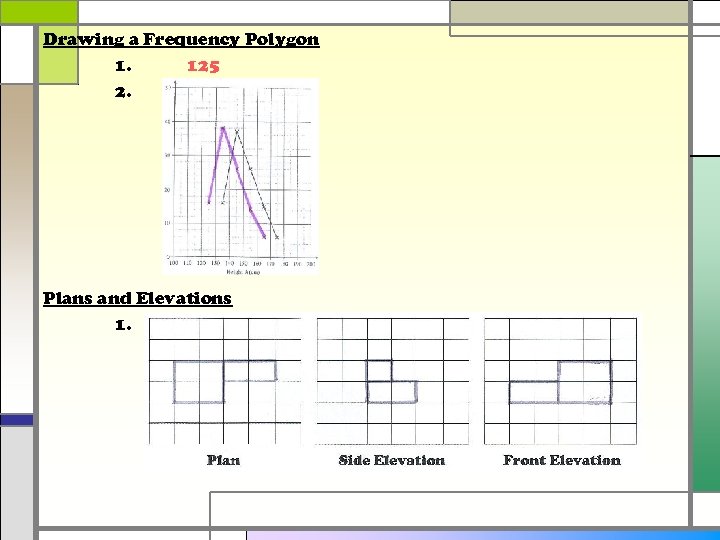Drawing a Frequency Polygon 1. 125 2. Plans and Elevations 1.

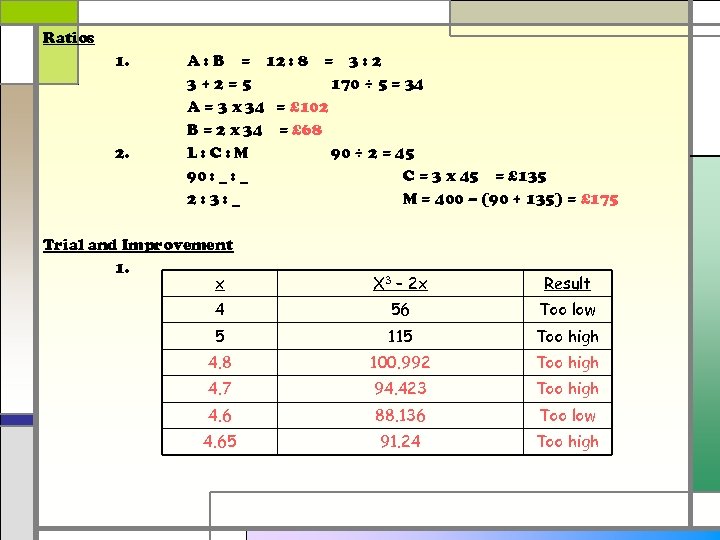Ratios 1. 2. A : B = 12 : 8 = 3 : 2 3+2=5 170 ÷ 5 = 34 A = 3 x 34 = £ 102 B = 2 x 34 = £ 68 L: C: M 90 ÷ 2 = 45 90 : _ C = 3 x 45 = £ 135 2: 3: _ M = 400 – (90 + 135) = £ 175 Trial and Improvement 1. x X 3 – 2 x Result 4 56 Too low 5 115 Too high 4. 8 100. 992 Too high 4. 7 94. 423 Too high 4. 6 88. 136 Too low 4. 65 91. 24 Too high

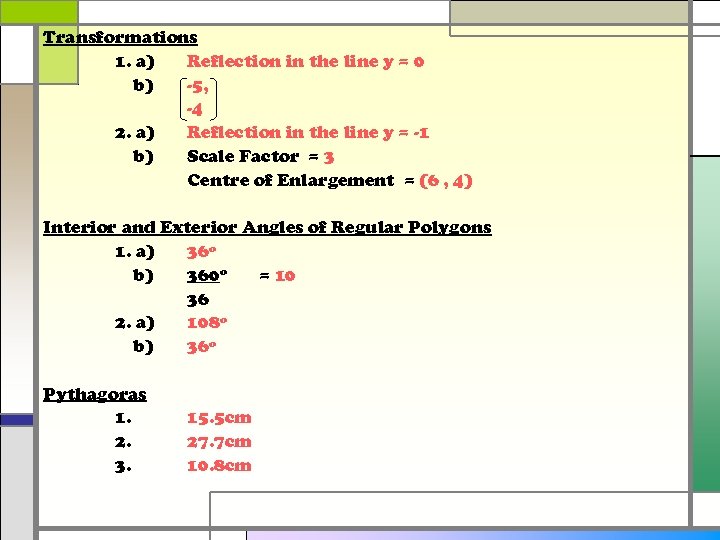Transformations 1. a) Reflection in the line y = 0 b) -5, -4 2. a) Reflection in the line y = -1 b) Scale Factor = 3 Centre of Enlargement = (6 , 4) Interior and Exterior Angles of Regular Polygons 1. a) 36 o b) 360 o = 10 36 2. a) 108 o b) 36 o Pythagoras 1. 2. 3. 15. 5 cm 27. 7 cm 10. 8 cm

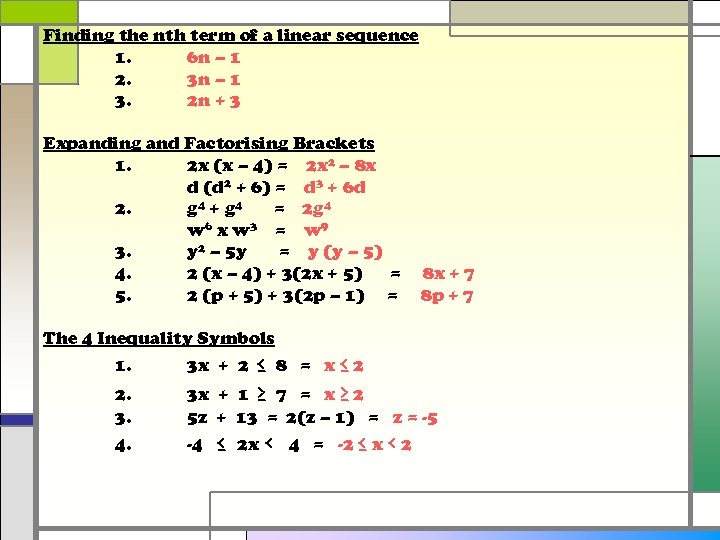Finding the nth term of a linear sequence 1. 6 n – 1 2. 3 n – 1 3. 2 n + 3 Expanding and Factorising Brackets 1. 2 x (x – 4) = 2 x 2 – 8 x d (d 2 + 6) = d 3 + 6 d 2. g 4 + g 4 = 2 g 4 w 6 x w 3 = w 9 3. y 2 – 5 y = y (y – 5) 4. 2 (x – 4) + 3(2 x + 5) = 5. 2 (p + 5) + 3(2 p – 1) = The 4 Inequality Symbols 1. 3 x + 2 ≤ ≥ 8 = x≤ 2 8 x + 7 8 p + 7 2. 3. 3 x + 1 7 = x≥ 2 5 z + 13 = 2(z – 1) = z = -5 4. -4 ≤ 2 x ‹ 4 = -2 ≤ x ‹ 2

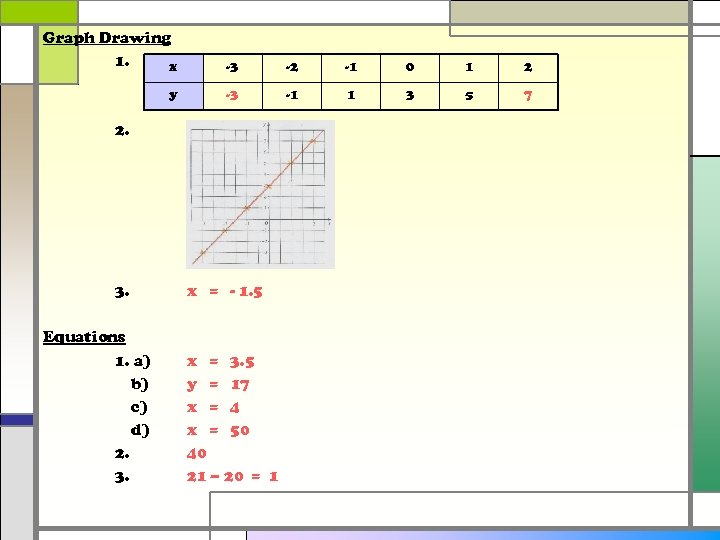Graph Drawing 1. x -3 -2 -1 0 1 2 y -3 -1 1 3 5 7 2. 3. Equations 1. a) b) c) d) 2. 3. x = - 1. 5 x = 3. 5 y = 17 x = 4 x = 50 40 21 – 20 = 1