Mathematics Statistics Topic 8 Hypothesis Testing

Mathematics & Statistics Topic 8 Hypothesis Testing

Topic Goals After completing this topic, you should be able to: n Formulate null and alternative hypotheses for applications involving a population mean from a normal distribution n a population proportion (large samples) n Formulate a decision rule for testing a hypothesis n Know how to use the critical value and p-value approaches to test the null hypothesis (for both mean and proportion problems) n Know what Type I and Type II errors are n Assess the power of a test n

What is a Hypothesis? n A hypothesis is a claim (assumption) about a population parameter: n population mean Example: The mean monthly cell phone bill in Dublin is more at least € 42, i. e. μ ≥ 42 n population proportion Example: The proportion of Irish voters in favour of a Dublin metro is 70%, i. e. p =. 70

Hypothesis testing Procedure n n Comparable to trial procedures Start with two hypotheses n n n Null hypothesis (defendent innocent) Alternative hypothesis (denfendent guilty) Initially assume that the null hypothesis is true n innocent until proven guilty Gather data (evidence) and compute sample statistics Decide to reject null hypothesis or not How to make such a decision?

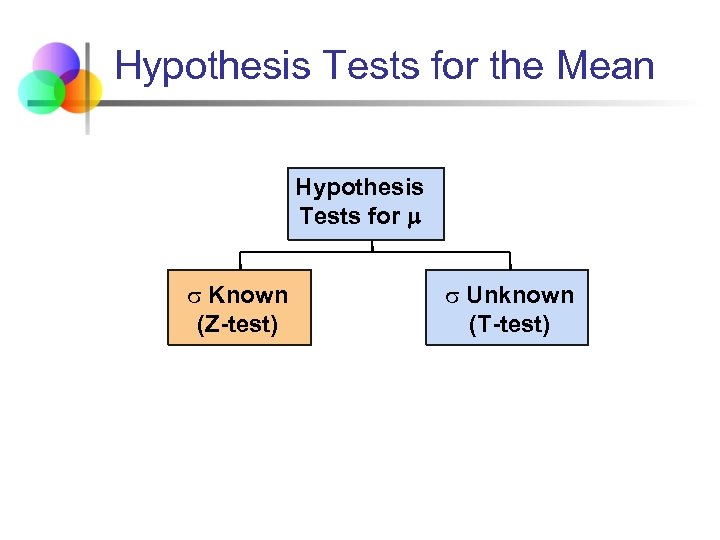Hypothesis Tests for the Mean Hypothesis Tests for Known (Z-test) Unknown (T-test)

The Null Hypothesis, H 0 n States the assumption (numerical) to be tested Example: The mean monthly cell phone bill in Dublin is μ ≥ € 42 ( ) n Is always about a population parameter, not about a sample statistic

The Null Hypothesis (continued) n n Refers to the status quo Always contains “=” , “≤” or “ ” sign May or may not be rejected Is generally the hypothesis that the researcher is trying to challenge

The Alternative Hypothesis, H 1 n Is the opposite of the null hypothesis n n n e. g. , The average phone bill in Dublin is less than € 42 ( H 1: μ < 42 ) Challenges the status quo Never contains the “=” , “≤” or “ ” sign May or may not be supported Is generally the hypothesis that the researcher is trying to support

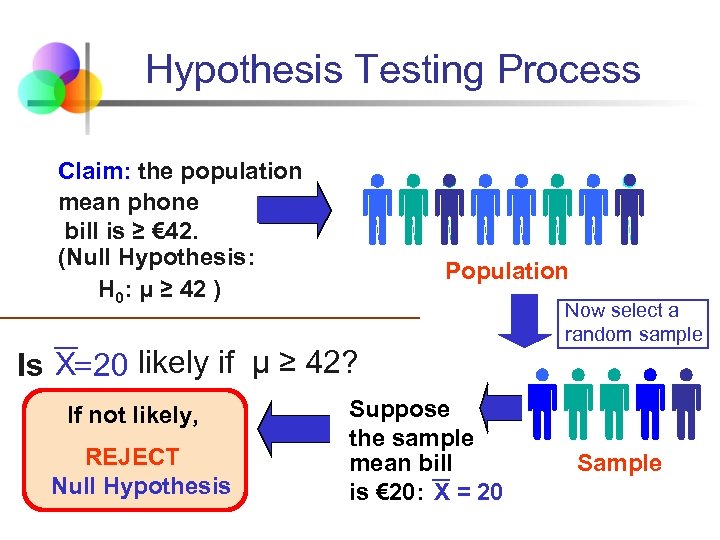Hypothesis Testing Process Claim: the population mean phone bill is ≥ € 42. (Null Hypothesis: H 0: μ ≥ 42 ) Population Is X= 20 likely if μ ≥ 42? If not likely, REJECT Null Hypothesis Suppose the sample mean bill is € 20: X = 20 Now select a random sample Sample

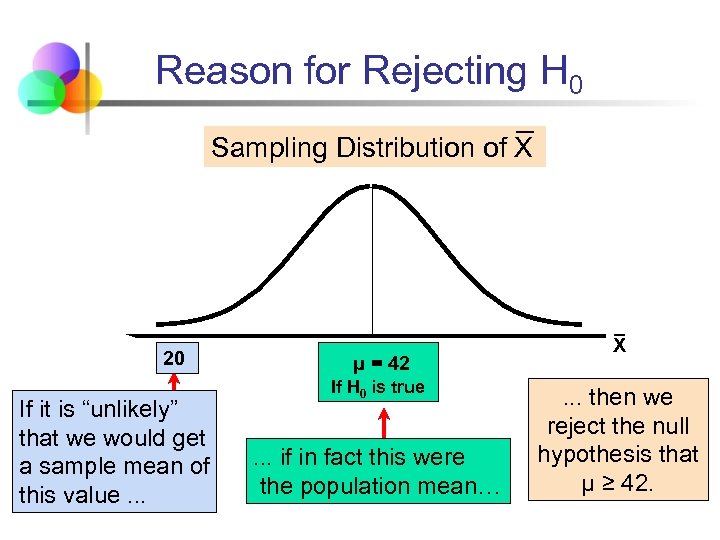Reason for Rejecting H 0 Sampling Distribution of X 20 If it is “unlikely” that we would get a sample mean of this value. . . μ = 42 If H 0 is true . . . if in fact this were the population mean… X . . . then we reject the null hypothesis that μ ≥ 42.

Main idea If X “too small”: reject H 0: μ ≥ 42

Example n Even if μ=42 is the true mean it is still possible that we observe a sample mean of 20 by sheer chance Suppose the amount of a phone bill in Dublin (call it X) is normal with (known) st. dev. σ=30. If n=9, we know that the sample mean is normal with n So, n n

Example (continued) n n n So, if we find a sample mean of 20 and if the population mean is 42. . . we have observed an event that occurs with probability. 0139. Do we deem this “unlikely”? Below what probability will we call an event “unlikely”? This threshold probability is chosen by the researcher and is called the. .

Level of Significance, n n The threshold probability below which we will judge observations to be “unlikely” Defines a rejection region of the sampling distribution n Values for the sample mean that are deemed “unlikely”. n Is denoted by , (level of significance) n Typical values are. 01, . 05, or. 10 n Is selected by the researcher before the test takes place n Provides the critical value(s) of the test

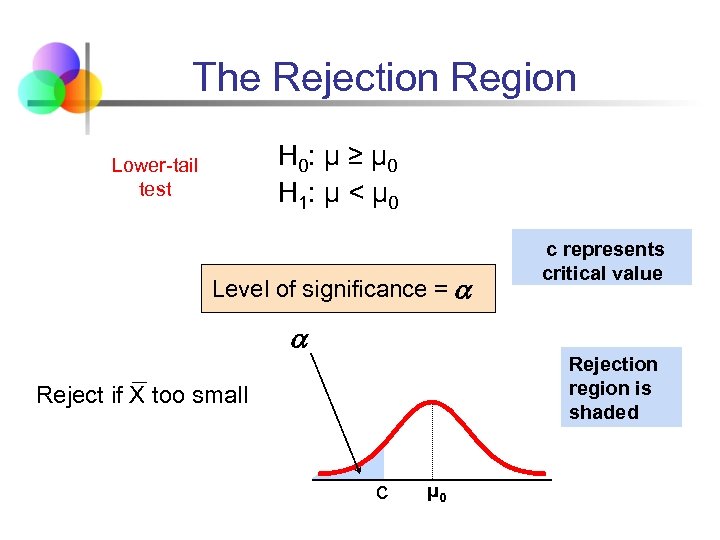The Rejection Region H 0: μ ≥ μ 0 H 1: μ < μ 0 Lower-tail test Level of significance = c represents critical value Rejection region is shaded Reject if X too small c μ 0

The Rejection region (continued) n n n So, given a level of significance α we find a value c for the sample mean sunch that smaller values occur with a (conditional) probability equal to α. . . given that the null hypothesis H 0 is true. In mathematical notation:

The Decision Rule n If we observe a value X < c then we know that: n n n either the null hypothesis is not true or we have observed an event that occurs with a probability less than α But we find events that occur with a probability less than α unlikely. . . and therefore we choose to reject H 0 instead. If X > c. . . we do not reject H 0.

How to find c? Let zα be such that Then we find that So, reject H 0 if n Recall that

Example n n H 0: μ ≥ 42 vs. H 1: μ < 42 Choose level α = 0. 05 Suppose X = 20, σ = 30, n = 9 Use Table 1 (or 8) to find that or P(Z<-zα)=α ↔ F(-z. 05) =. 05 ↔ -z. 05 = -1. 645 n Note that So, we reject H 0 and say that the mean monthly phone bill in Dublin is significantly lower than 42 at the 5% level

Summary: Test of Hypothesis for the Mean (σ Known) n Convert sample result ( ) to a z value Hypothesis Tests for σ Known σ Unknown Consider the test The decision rule is: (Assume the population is normal)

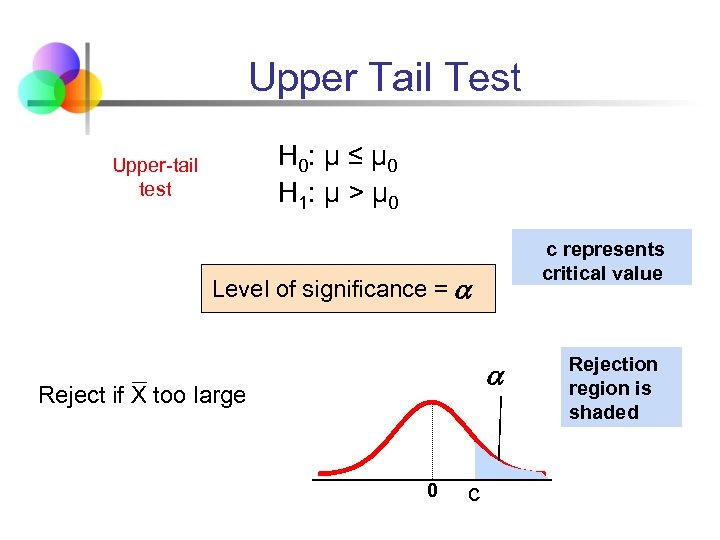Upper Tail Test H 0: μ ≤ μ 0 H 1: μ > μ 0 Upper-tail test c represents critical value Level of significance = Reject if X too large 0 c Rejection region is shaded

Upper Tail Test (continued) n n n This is the mirror image of the Lower Tail test. So, reject H 0 if Z is large. How large?

Example: Upper-Tail Z Test for Mean ( Known) A phone industry manager thinks that customer monthly cell phone bill have increased, and now average over € 52 per month. The company wishes to test this claim. (Assume = 10 is known) Form hypothesis test: H 0: μ ≤ 52 the average is not over € 52 per month H 1: μ > 52 the average is greater than € 52 per month (i. e. , sufficient evidence exists to support the manager’s claim)

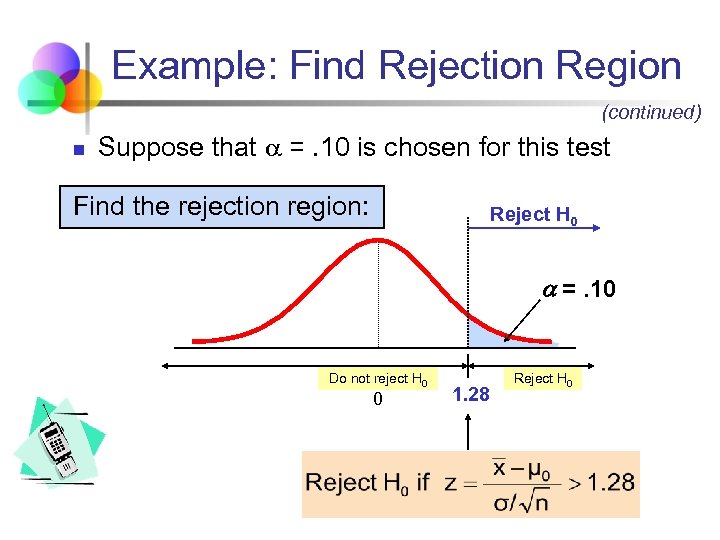Example: Find Rejection Region (continued) n Suppose that =. 10 is chosen for this test Find the rejection region: Reject H 0 =. 10 Do not reject H 0 0 1. 28 Reject H 0

Example: Sample Results (continued) Obtain sample and compute the test statistic Suppose a sample is taken with the following results: n = 64, x = 53. 1 ( =10 was assumed known) n Using the sample results,

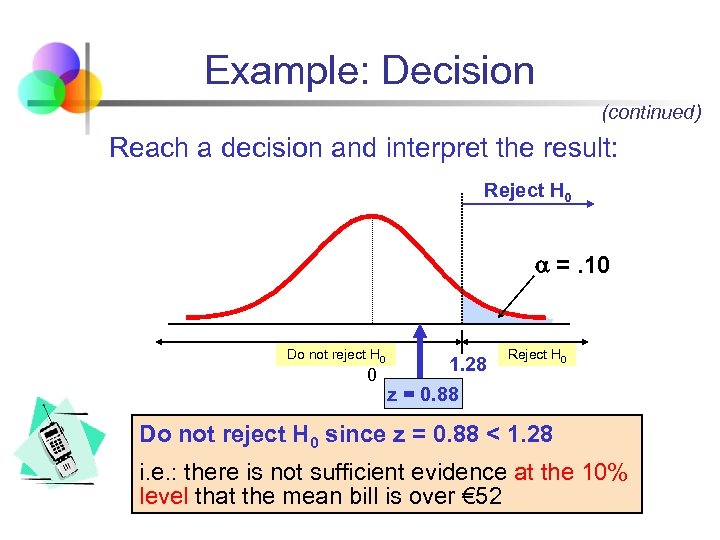Example: Decision (continued) Reach a decision and interpret the result: Reject H 0 =. 10 Do not reject H 0 1. 28 0 z = 0. 88 Reject H 0 Do not reject H 0 since z = 0. 88 < 1. 28 i. e. : there is not sufficient evidence at the 10% level that the mean bill is over € 52

Test of Hypothesis for the Mean (σ Known) n Convert sample result ( ) to a z value Hypothesis Tests for σ Known σ Unknown Consider the test The decision rule is: (Assume the population is normal)

p-Value Approach to Testing n p-value: Probability of obtaining a test statistic more extreme ( ≤ or ) than the observed sample value given H 0 is true n n Also called observed level of significance Smallest value of for which H 0 can be rejected

p-Value Approach to Testing (continued) n n n Convert sample result (e. g. , statistic ) ) to test statistic (e. g. , z Obtain the p-value n For an upper tail test: Decision rule: compare the p-value to n If p-value < , reject H 0 n If p-value , do not reject H 0

Example: Upper-Tail Z Test for Mean ( Known) A phone industry manager thinks that customer monthly cell phone bill have increased, and now average over € 52 per month. The company wishes to test this claim. (Assume = 10 is known) Form hypothesis test: H 0: μ ≤ 52 the average is not over € 52 per month H 1: μ > 52 the average is greater than € 52 per month (i. e. , sufficient evidence exists to support the manager’s claim)

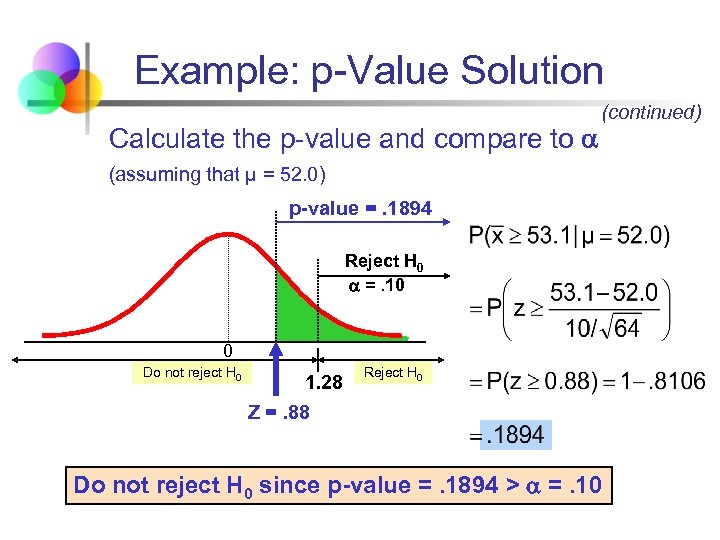Example: p-Value Solution Calculate the p-value and compare to (continued) (assuming that μ = 52. 0) p-value =. 1894 Reject H 0 =. 10 0 Do not reject H 0 1. 28 Z =. 88 Reject H 0 Do not reject H 0 since p-value =. 1894 > =. 10

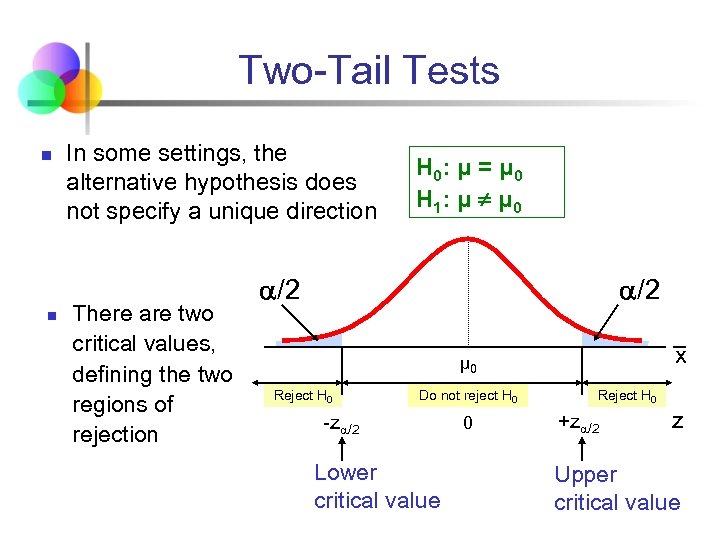Two-Tail Tests n n In some settings, the alternative hypothesis does not specify a unique direction There are two critical values, defining the two regions of rejection H 0: μ = μ 0 H 1: μ ¹ μ 0 /2 x μ 0 Reject H 0 Do not reject H 0 -z /2 Lower critical value 0 Reject H 0 +z /2 z Upper critical value

Two Tail Test (continued) n n n This is a combination of the Upper and Lower Tail tests. So, reject H 0 either if Z is small or large. How small or large?

Hypothesis Testing Example Test the claim that the true mean # of TV sets in Irish homes is equal to 3. (Assume σ = 0. 8) n n n State the appropriate null and alternative hypotheses n H 0: μ = 3 , H 1: μ ≠ 3 (This is a two tailed test) Specify the desired level of significance n Suppose that =. 05 is chosen for this test Choose a sample size n Suppose a sample of size n = 100 is selected

Hypothesis Testing Example (continued) n n n Determine the appropriate technique n σ is known so this is a z test Set up the critical values n For =. 05 the critical z values are ± 1. 96 Collect the data and compute the test statistic n Suppose the sample results are n = 100, x = 2. 84 (σ = 0. 8 is assumed known) So the test statistic is:

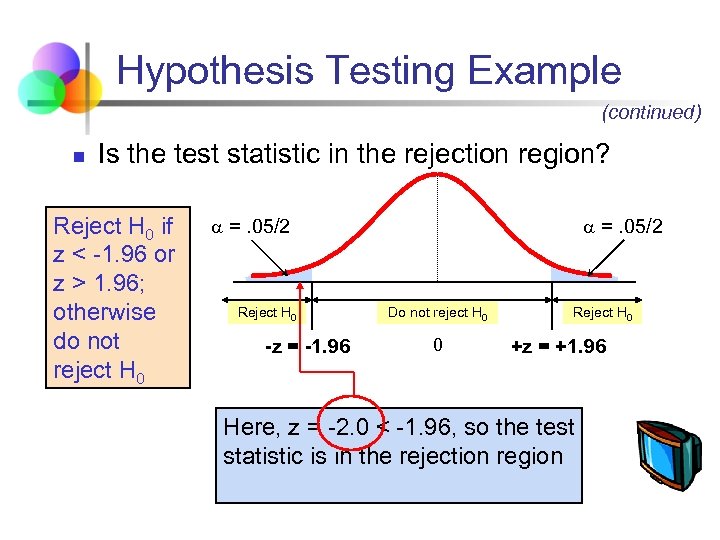Hypothesis Testing Example (continued) n Is the test statistic in the rejection region? Reject H 0 if z < -1. 96 or z > 1. 96; otherwise do not reject H 0 =. 05/2 Reject H 0 -z = -1. 96 =. 05/2 Do not reject H 0 0 Reject H 0 +z = +1. 96 Here, z = -2. 0 < -1. 96, so the test statistic is in the rejection region

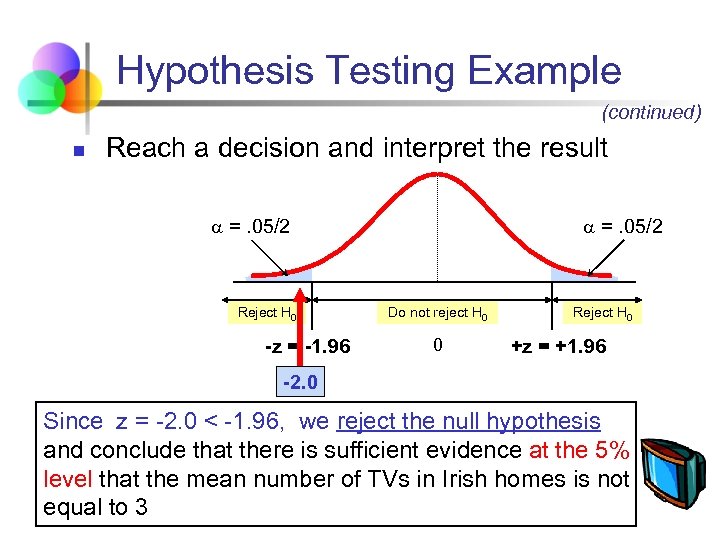Hypothesis Testing Example (continued) n Reach a decision and interpret the result =. 05/2 Reject H 0 -z = -1. 96 =. 05/2 Do not reject H 0 0 Reject H 0 +z = +1. 96 -2. 0 Since z = -2. 0 < -1. 96, we reject the null hypothesis and conclude that there is sufficient evidence at the 5% level that the mean number of TVs in Irish homes is not equal to 3

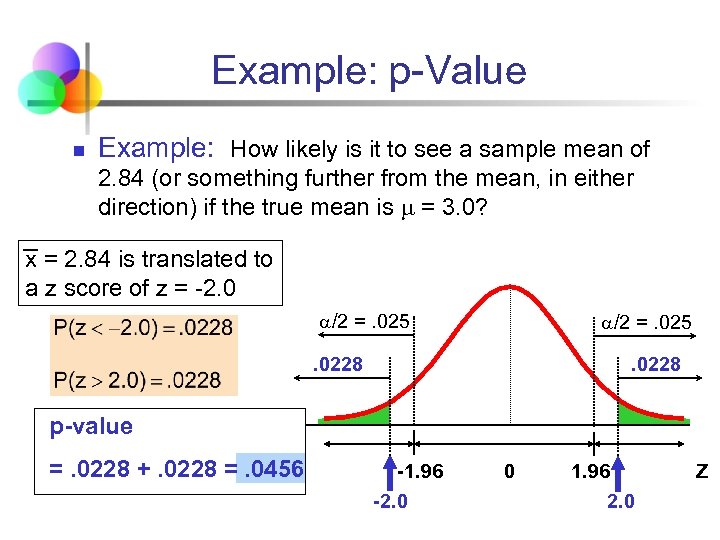Example: p-Value n Example: How likely is it to see a sample mean of 2. 84 (or something further from the mean, in either direction) if the true mean is = 3. 0? x = 2. 84 is translated to a z score of z = -2. 0 /2 =. 025 . 0228 p-value =. 0228 +. 0228 =. 0456 -1. 96 -2. 0 0 1. 96 2. 0 Z

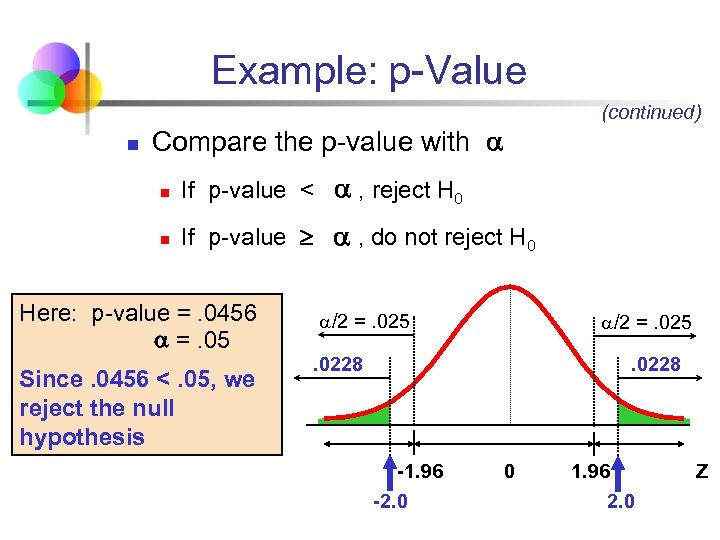Example: p-Value n (continued) Compare the p-value with n If p-value < , reject H 0 n If p-value , do not reject H 0 Here: p-value =. 0456 =. 05 Since. 0456 <. 05, we reject the null hypothesis /2 =. 025 . 0228 -1. 96 -2. 0 0 1. 96 2. 0 Z

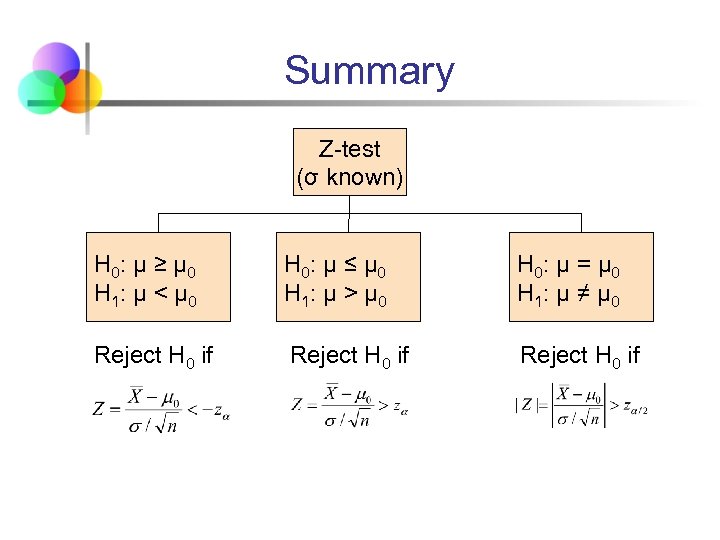Summary Z-test (σ known) H 0: μ ≥ μ 0 H 1: μ < μ 0 H 0: μ ≤ μ 0 H 1: μ > μ 0 H 0: μ = μ 0 H 1: μ ≠ μ 0 Reject H 0 if

Hypothesis Tests for the Mean Hypothesis Tests for Known (Z-test) Unknown (T-test)

General idea n n Exactly the same as before. . . except that we don’t know σ. . . and therefore cannot use Z. However, we do know that

T-test for the mean of a normal T-test (σ unknown) H 0: μ ≥ μ 0 H 1: μ < μ 0 H 0: μ ≤ μ 0 H 1: μ > μ 0 H 0: μ = μ 0 H 1: μ ≠ μ 0 Reject H 0 if

Example: Two-Tail Test ( Unknown) The average cost of a hotel room in New York is said to be $168 per night. A random sample of 25 hotels resulted in x = $172. 50 and s = $15. 40. Test at the = 0. 05 level. (Assume the population distribution is normal) H 0: μ = 168 H 1: μ ¹ 168

Example Solution: Two-Tail Test H 0: μ = 168 H 1: μ ¹ 168 n = 0. 05 n n = 25 n is unknown, so use a t statistic /2=. 025 Reject H 0 -t n-1, α/2 -2. 0639 /2=. 025 Do not reject H 0 0 1. 46 Reject H 0 t n-1, α/2 2. 0639 n Critical Value: t 24 , . 025 = ± 2. 0639 Do not reject H 0: not sufficient evidence at the 5% level that true mean cost is different from $168

Tests of the Population Proportion n Involves categorical variables n Two possible outcomes n n “Success” (a certain characteristic is present) “Failure” (the characteristic is not present) Fraction or proportion of the population in the “success” category is denoted by p Assume sample size is large

Proportions (continued) n Sample proportion in the success category is denoted by n n When np(1 – p) > 9, can be approximated by a normal distribution with mean and standard deviation n

Hypothesis Tests for Proportions n The sampling distribution of is Hypothesis approximately Tests for P normal, so the test statistic is a z n. P(1 – P) < 9 n. P(1 – P) > 9 value: Not discussed in this course

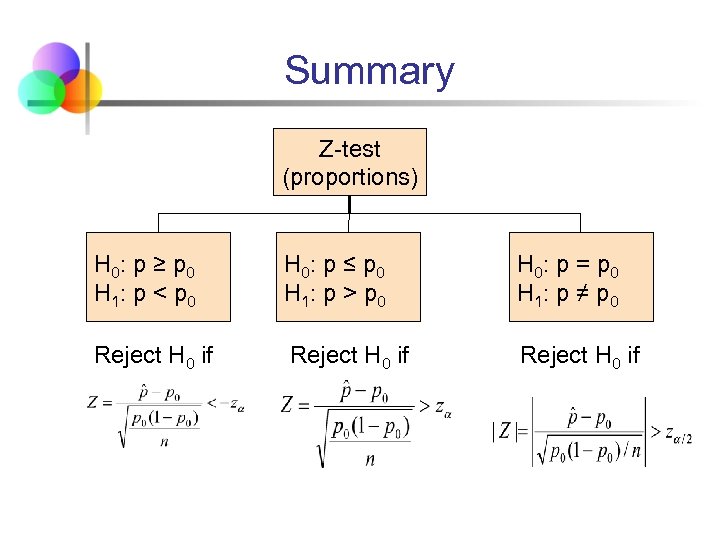Summary Z-test (proportions) H 0: p ≥ p 0 H 1: p < p 0 H 0: p ≤ p 0 H 1: p > p 0 H 0: p = p 0 H 1: p ≠ p 0 Reject H 0 if

Example: Z Test for Proportion A marketing company claims that it receives 8% responses from its mailing. To test this claim, a random sample of 500 were surveyed with 25 responses. Test at the =. 05 significance level. Check: Our approximation for p is = 25/500 =. 05 np(1 - p) = (500)(. 05)(. 95) = 23. 75 > 9

Z Test for Proportion: Solution Test Statistic: H 0: p =. 08 H 1: p ¹. 08 =. 05 n = 500, =. 05 Decision: Critical Values: ± 1. 96 Reject . 025 -1. 96 -2. 47 0 1. 96 z Reject H 0 at =. 05 Conclusion: There is evidence at the 5% level to reject the company’s claim of 8% response rate.

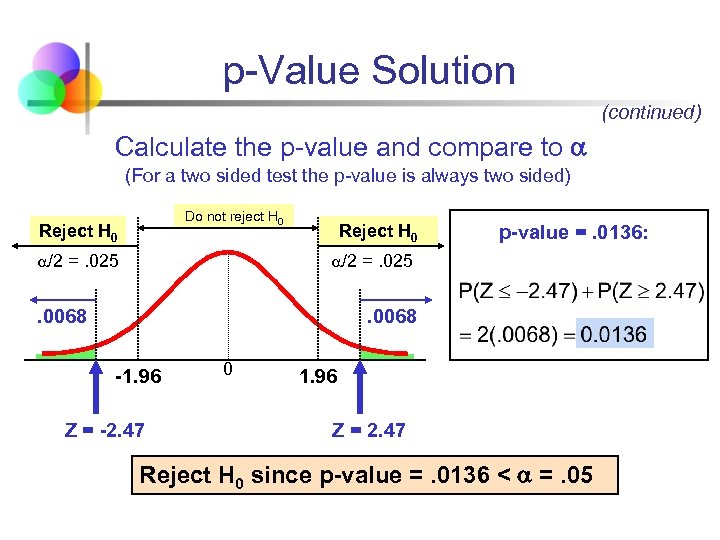p-Value Solution (continued) Calculate the p-value and compare to (For a two sided test the p-value is always two sided) Do not reject H 0 Reject H 0 /2 =. 025 Reject H 0 p-value =. 0136: /2 =. 025 . 0068 -1. 96 Z = -2. 47 0 1. 96 Z = 2. 47 Reject H 0 since p-value =. 0136 < =. 05

Errors in Making Decisions n n Type I Error n Reject a true null hypothesis n Considered a serious type of error Since we reject H 0 if the statistic is in the rejection region, we know that: The probability of Type I Error is n That’s how we chose α in the first place!

Errors in Making Decisions (continued) n Type II Error n Fail to reject a false null hypothesis The probability of Type II Error is β

Outcomes and Probabilities Possible Hypothesis Test Outcomes Actual Situation Decision Key: Outcome (Probability) H 0 True H 0 False Do Not Reject H 0 No error (1 - ) Type II Error (β) Reject H 0 Type I Error ( ) No Error (1 -β)

Type I & II Error Relationship § Type I and Type II errors can not happen at the same time § Type I error can only occur if H 0 is true § Type II error can only occur if H 0 is false If Type I error probability ( ) Type II error probability ( β ) , then

Power of the Test n n The power of a test is the probability of rejecting a null hypothesis that is false i. e. , n Power = P(Reject H 0 | H 1 is true) Power of the test increases as the sample size increases

Power of the Test n Recall the possible hypothesis test outcomes: Actual Situation n n H 0 True H 0 False Do Not Reject H 0 No error (1 - ) Type II Error (β) Reject H 0 Key: Outcome (Probability) Decision Type I Error ( ) No Error (1 -β) β denotes the probability of Type II Error 1 – β is defined as the power of the test Power = 1 – β = the probability that a false null hypothesis is rejected

Type II Error Assume the population is normal and the population variance is known. Consider the test The decision rule is: or If the null hypothesis is false and the true mean is μ*, then the probability of type II error is

Type II Error Example n Type II error is the probability of failing to reject a false H 0 Suppose we fail to reject H 0: μ 52 when in fact the true mean is μ* = 50 Reject H 0: μ 52 52 Do not reject H 0 : μ 52

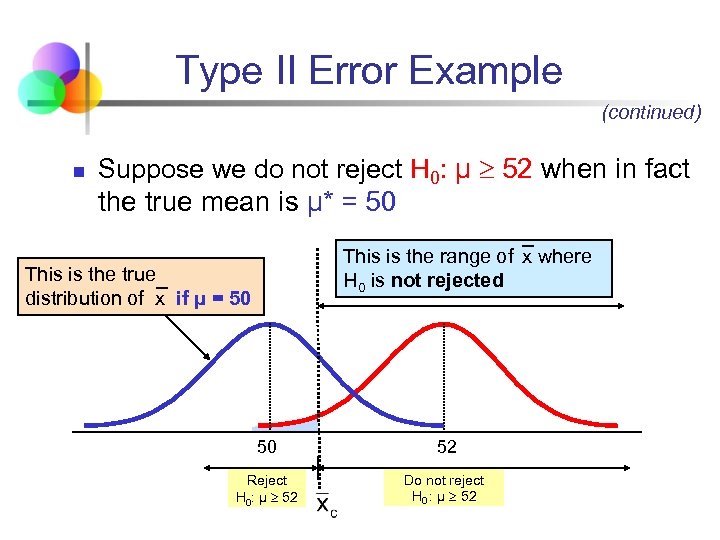Type II Error Example (continued) n Suppose we do not reject H 0: μ 52 when in fact the true mean is μ* = 50 This is the range of x where H 0 is not rejected This is the true distribution of x if μ = 50 50 52 Reject H 0: μ 52 Do not reject H 0 : μ 52

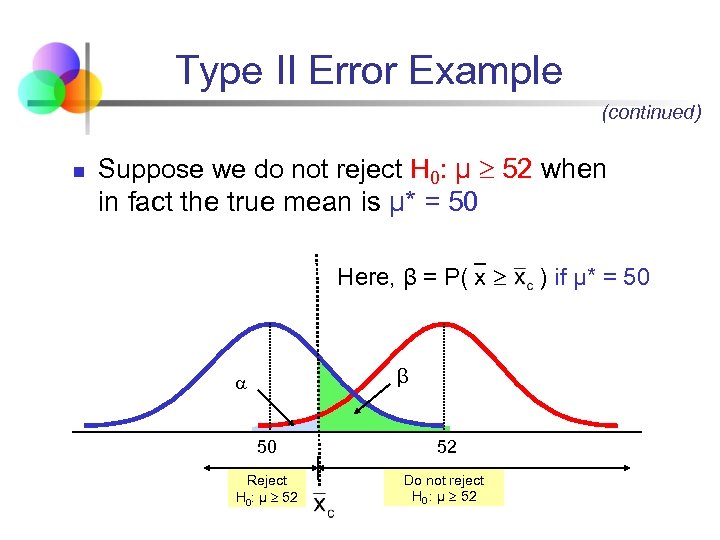Type II Error Example (continued) n Suppose we do not reject H 0: μ 52 when in fact the true mean is μ* = 50 Here, β = P( x β 50 52 Reject H 0: μ 52 Do not reject H 0 : μ 52 ) if μ* = 50

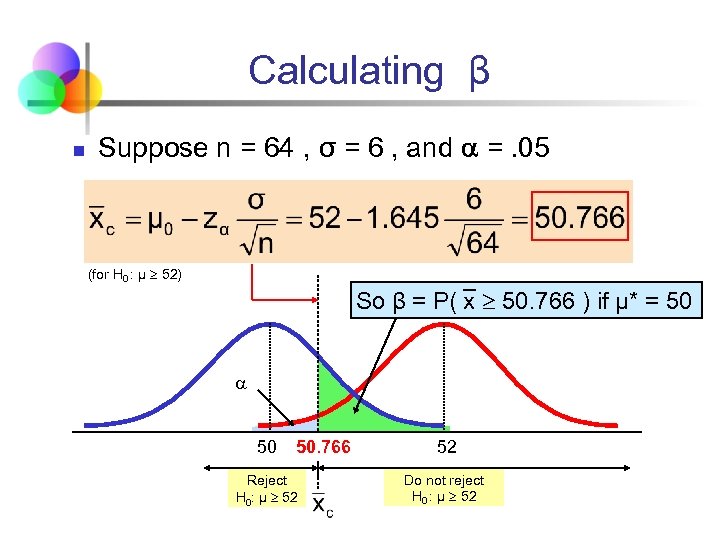Calculating β n Suppose n = 64 , σ = 6 , and =. 05 (for H 0 : μ 52) So β = P( x 50. 766 ) if μ* = 50 50. 766 Reject H 0: μ 52 52 Do not reject H 0 : μ 52

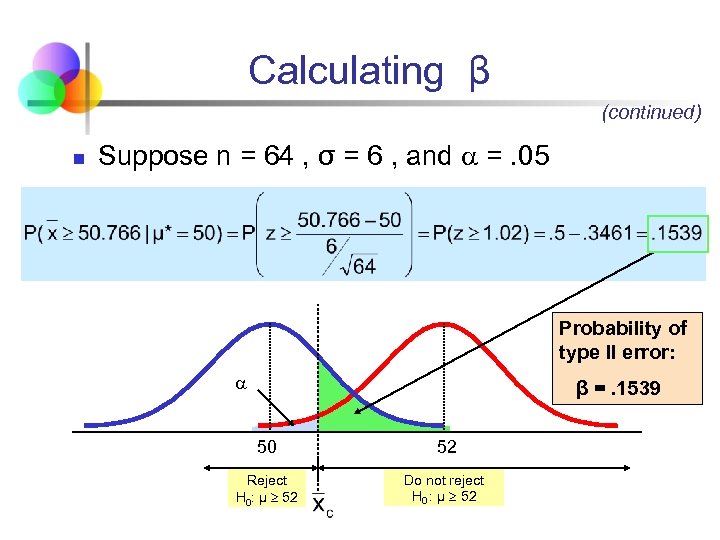Calculating β (continued) n Suppose n = 64 , σ = 6 , and =. 05 Probability of type II error: β =. 1539 50 52 Reject H 0: μ 52 Do not reject H 0 : μ 52

Power of the Test Example If the true mean is μ* = 50, n The probability of Type II Error = β = 0. 1539 n The power of the test = 1 – β = 1 – 0. 1539 = 0. 8461 Actual Situation Key: Outcome (Probability) Decision H 0 True Do Not Reject H 0 No error 1 - = 0. 95 Reject H 0 Type I Error = 0. 05 H 0 False Type II Error β = 0. 1539 No Error 1 - β = 0. 8461 (The value of β and the power will be different for each μ*)

The Godfather Some of the Dons of important mafia families claim that Don Corleone does not bring in the promised $5 mln in “transactions”. Corleone orders his consiglieri to investigate. Tom Hagen asks you You can sample 16 transactions

The Godfather (continued) n Construct hypotheses n n Choose level of significance n n n H 0: μ ≤ 5 and H 1: μ > 5 (upper tail test) α =. 005 (you want to be VERY careful) Suppose you observe X = 5. 9 mln with st. dev. s. X = 1. 16 mln. Since variance unknown: n n use t-test (assume that X is normal)

The Godfather (continued) Reject if: Cut-off point: test statistic: Decision: Reject H 0: there is evidence at the. 5% level that the true mean income is larger than 5 mln.

Misdiagnosis Someone claims that the number of misdiagnoses in a particular hospital is significantly higher than elsewhere. You do some research and find that a “normal” rate of misdiagnosis is 1%. You take a sample of 150 cases and find 3 cases of misdiagnosis. Can this be due to chance? Use test for proportions. H 0: p =. 01 and H 1: p ≠. 01 Take α =. 1 So zα/2 = z. 05 = 1. 645

Misdiagnosis (continued) There is no evidence at the 10% level that the misdiagnosis rate is significantly different from 1%. So it could be down to “bad luck”

Misdiagnosis (continued) 90% confidence interval [. 0012, . 0388] Note that the 1% rate lies within the interval. That’s why we can’t reject.

Errors in Making Decisions n n Type I Error n Reject a true null hypothesis n Considered a serious type of error Since we reject H 0 if the statistic is in the rejection region, we know that: The probability of Type I Error is n That’s how we chose α in the first place!

Errors in Making Decisions (continued) n Type II Error n Fail to reject a false null hypothesis The probability of Type II Error is denoted by β

Outcomes and Probabilities Possible Hypothesis Test Outcomes Actual Situation Decision Key: Outcome (Probability) H 0 True H 0 False Do Not Reject H 0 No error (1 - ) Type II Error (β) Reject H 0 Type I Error ( ) No Error (1 -β)

Type I & II Error Relationship § Type I and Type II errors can not happen at the same time § Type I error can only occur if H 0 is true § Type II error can only occur if H 0 is false If Type I error probability ( ) Type II error probability ( β ) , then

Power of the Test n n The power of a test is the probability of rejecting a null hypothesis that is false i. e. , n Power = P(Reject H 0 | H 1 is true) Power of the test increases as the sample size increases

Power of the Test n Recall the possible hypothesis test outcomes: Actual Situation n n H 0 True H 0 False Do Not Reject H 0 No error (1 - ) Type II Error (β) Reject H 0 Key: Outcome (Probability) Decision Type I Error ( ) No Error (1 -β) β denotes the probability of Type II Error 1 – β is defined as the power of the test Power = 1 – β = the probability that a false null hypothesis is rejected

Type II Error Assume the population is normal and the population variance is known. Consider the (lower-tail) test The decision rule is: or If the null hypothesis is false and the true mean is μ*, then the probability of type II error is

Type II Error Example n Type II error is the probability of failing to reject a false H 0 Suppose we fail to reject H 0: μ 52 when in fact the true mean is μ* = 50 Reject H 0: μ 52 52 Do not reject H 0 : μ 52

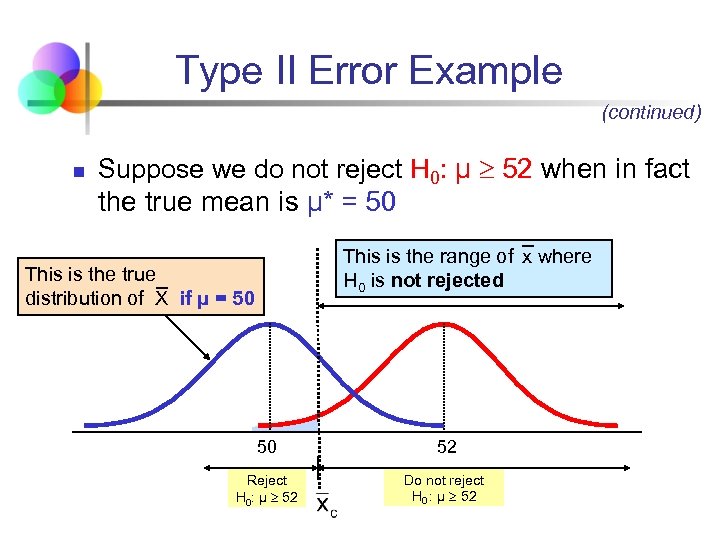Type II Error Example (continued) n Suppose we do not reject H 0: μ 52 when in fact the true mean is μ* = 50 This is the range of x where H 0 is not rejected This is the true distribution of X if μ = 50 50 52 Reject H 0: μ 52 Do not reject H 0 : μ 52

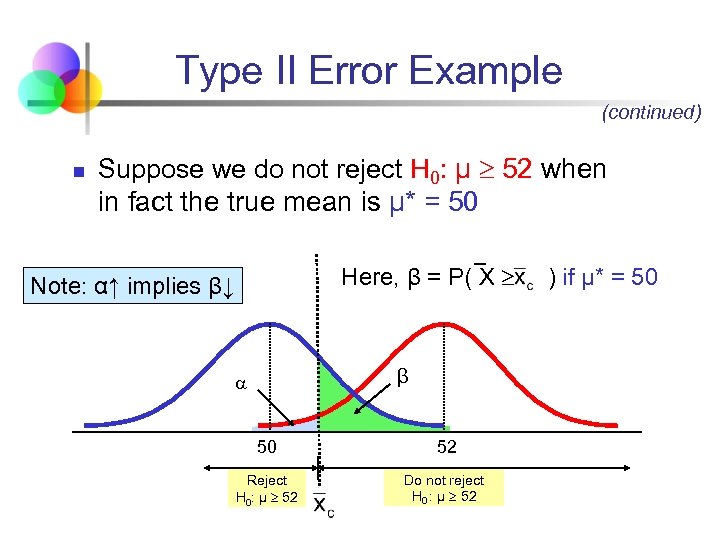Type II Error Example (continued) n Suppose we do not reject H 0: μ 52 when in fact the true mean is μ* = 50 Here, β = P( X Note: α↑ implies β↓ β 50 52 Reject H 0: μ 52 Do not reject H 0 : μ 52 ) if μ* = 50

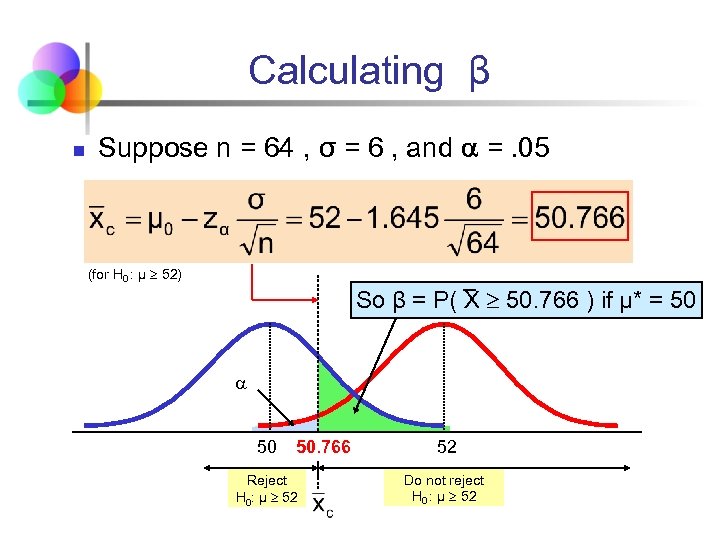Calculating β n Suppose n = 64 , σ = 6 , and =. 05 (for H 0 : μ 52) So β = P( X 50. 766 ) if μ* = 50 50. 766 Reject H 0: μ 52 52 Do not reject H 0 : μ 52

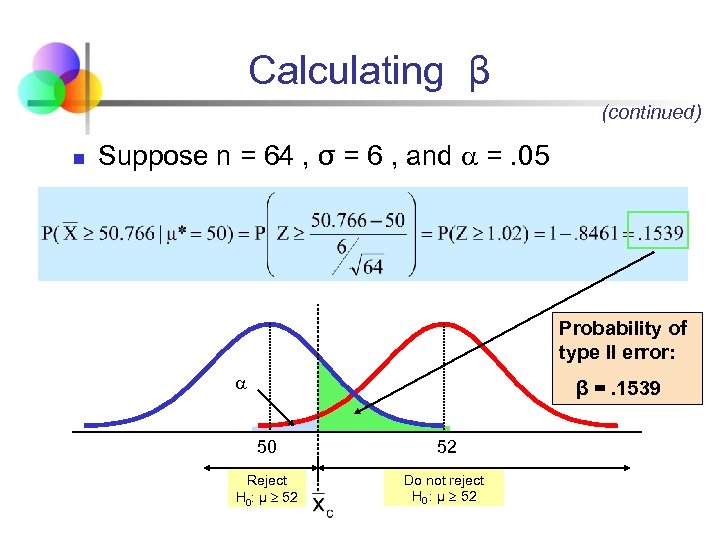Calculating β (continued) n Suppose n = 64 , σ = 6 , and =. 05 Probability of type II error: β =. 1539 50 52 Reject H 0: μ 52 Do not reject H 0 : μ 52

Power of the Test Example If the true mean is μ* = 50, n The probability of Type II Error = β = 0. 1539 n The power of the test = 1 – β = 1 – 0. 1539 = 0. 8461 Actual Situation Key: Outcome (Probability) Decision H 0 True Do Not Reject H 0 No error 1 - = 0. 95 Reject H 0 Type I Error = 0. 05 H 0 False Type II Error β = 0. 1539 No Error 1 - β = 0. 8461 (The value of β and the power will be different for each μ*)

Topic Summary n Addressed hypothesis testing methodology n Performed Z Test for the mean (σ known) n Discussed critical value and p-value approaches to hypothesis testing n Performed one-tail and two-tail tests n Performed t test for the mean (σ unknown) n Performed Z test for the proportion n Discussed type II error and power of the test