Mathematics in Virtual Knowledge Spaces Ontological Structures of

Mathematics in Virtual Knowledge Spaces Ontological Structures of Mathematical Content MMISS-Meeting Bremen 21 -22. April 2004 Dr. Sabina Jeschke

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Outline: Part A: Background Part B: The „Mumie“ – A Virtual Knowledge Space for Mathematics Part C: Structures of Mathematical Content Part D: Next Steps - Vision Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Part A: Background Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content „Change in mathematical Power“ (II). . . leads to: Changes in the fields of mathematics: - RESEARCH § § Changes in mathematical education - EDUCATION - Development of new fields of research Development of new methods of research Sabina Jeschke § § Expansion of necessary mathematical competences Development of new teaching and learning TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content New Focus on Mathematical Competence: • • Understanding of the potential and performance of mathematics Formulating, modelling and solving problems within a given context Mathematical thinking and drawing of conclusions Understanding of the interrelations between mathematical concepts and ideas Mastery of mathematical symbols and formalisms Communication through and about mathematics Reflected application of mathematical tools and software for Mathematicians AND Sabina Jeschke Oriented towards understanding Independence in the learning process Interdisziplinarity and Soft Skills for Users of Mathematics! TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Potential of Digital Media (within the context e. Learning, e. Teaching & e. Research) Modelling (Simulation, Numerics, Visualisation) Interactivity (Experiment, Exploration, Instruction) Pedagogical & Educational Cooperation (Communication, Collaboration, Coordination) Aspects Adaptability (Learning styles & individual requirements) Organisational Reusability & Recomposition Continous Availability (platform independence) Sabina Jeschke TU Berlin & Logistical Aspects

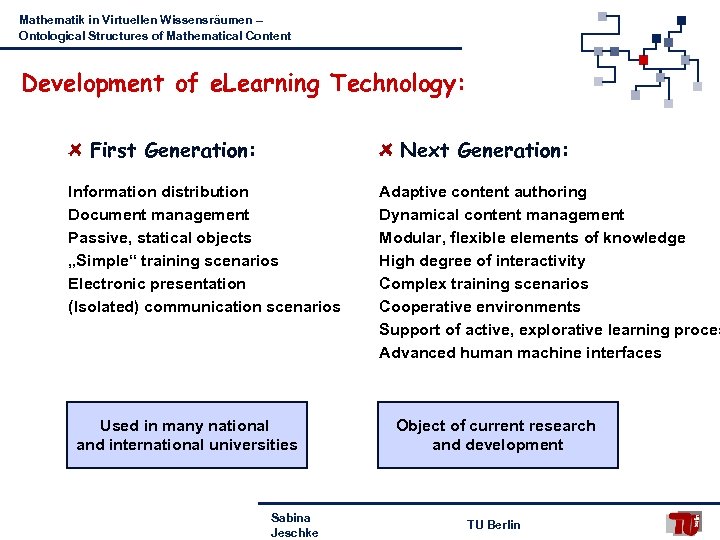Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Development of e. Learning Technology: First Generation: Next Generation: Information distribution Document management Passive, statical objects „Simple“ training scenarios Electronic presentation (Isolated) communication scenarios Used in many national and international universities Sabina Jeschke Adaptive content authoring Dynamical content management Modular, flexible elements of knowledge High degree of interactivity Complex training scenarios Cooperative environments Support of active, explorative learning proces Advanced human machine interfaces Object of current research and development TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content We have to face a huge divergence between potential and reality! So far: The Potential of Electronic Media in Education is Dramatically Wasted Sabina Jeschke TU Berlin !

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content (Technical) Causes for the Divergence: Monolithic design of most e. Learning software Open heterogeneous platformindependent portal solutions integrating virtual cooperative knowledge spaces Missing granularity and missing ontological structure of contents Analysis of self-immanent structures within fields of knowledge and development of granular elements of knowledge Use of statical typographic objects Use of active, executable objects and processes with semantic description Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Part B: The „Mumie“ – A Virtual Knowledge Space for Mathematics Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie - Philosophy: General Design Approaches: Pedagogical Concept: • Support of multiple learning scenarios • Support of classroom teaching • Open Source • Visualisation of intradisciplinary relations • Nonlinear navigation • Visualisation of mathematical objects and concepts • Support of experimental scenarios • Support of explorative learning • Adaptation to individual learning processes Content Technical Concept: • Field-specific database structure • XML technology • Dynamic „on-the-fly“ page generation • Strict division between content, context & presentation • Customisable presentation • Math. ML for mathematical symbols • La. Te. X (mm. Te. X) as authoring tool • Transparency and heterogenerity Sabina Jeschke Guidelines: • Modularity - Granularity • Mathematical rigidness and precision • Division between teacher and author • Division between content and application • Strict division between content and context TU Berlin

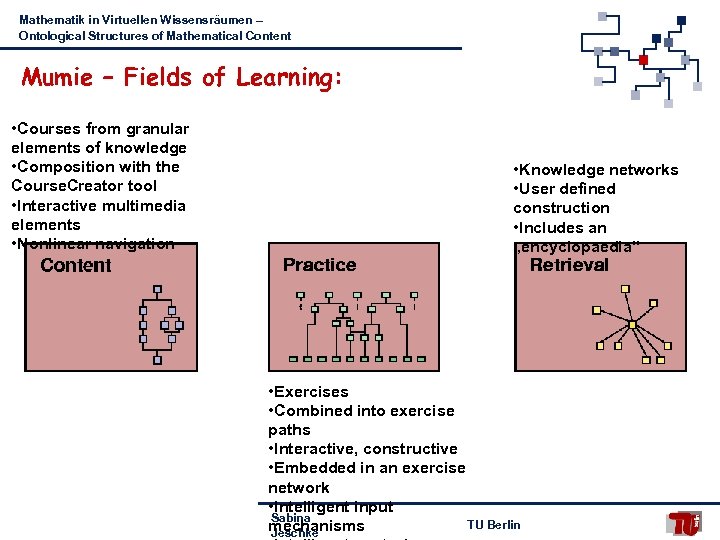Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie – Fields of Learning: • Courses from granular elements of knowledge • Composition with the Course. Creator tool • Interactive multimedia elements • Nonlinear navigation • Knowledge networks • User defined construction • Includes an „encyclopaedia“ • Exercises • Combined into exercise paths • Interactive, constructive • Embedded in an exercise network • Intelligent input Sabina TU Berlin mechanisms Jeschke

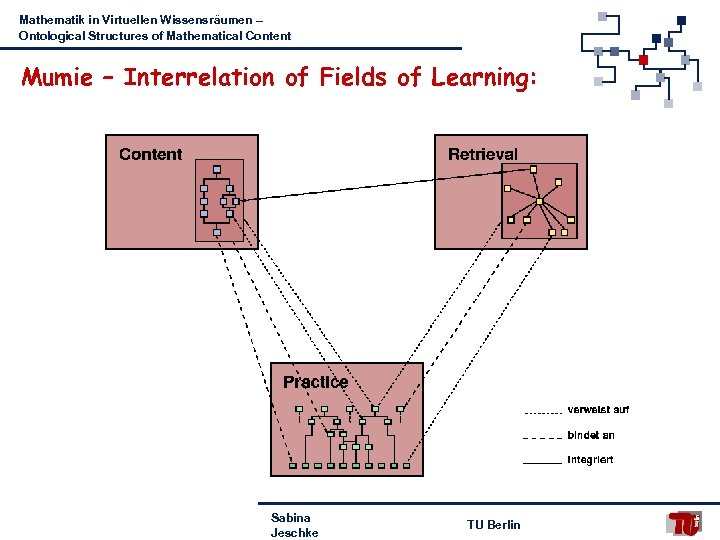Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie – Interrelation of Fields of Learning: Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie (Content) - Course. Creator: Course with content Course without content Sabina Jeschke TU Berlin

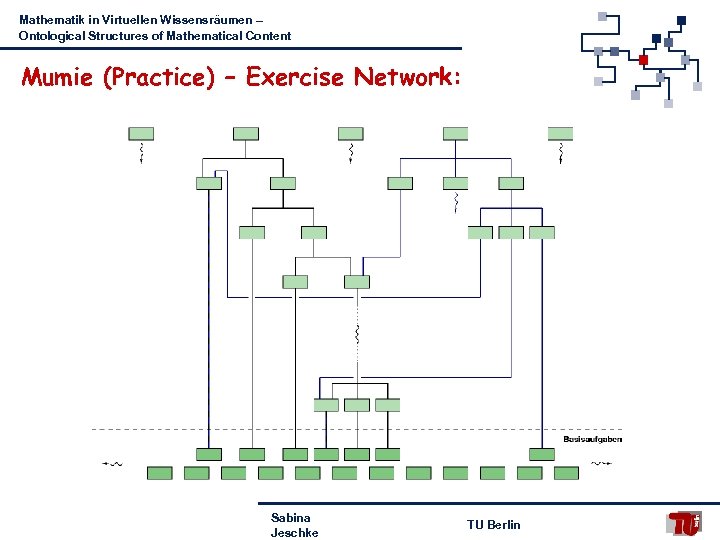Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie (Practice) – Exercise Network: Sabina Jeschke TU Berlin

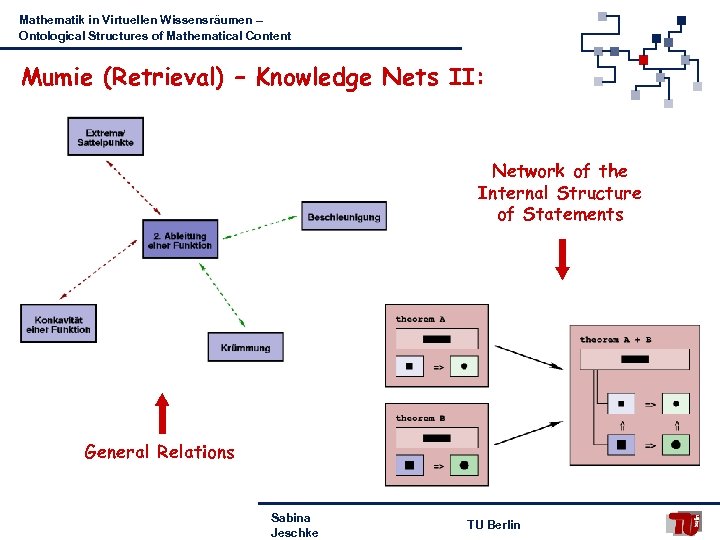Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie (Retrieval) – Knowledge Nets II: Network of the Internal Structure of Statements General Relations Sabina Jeschke TU Berlin

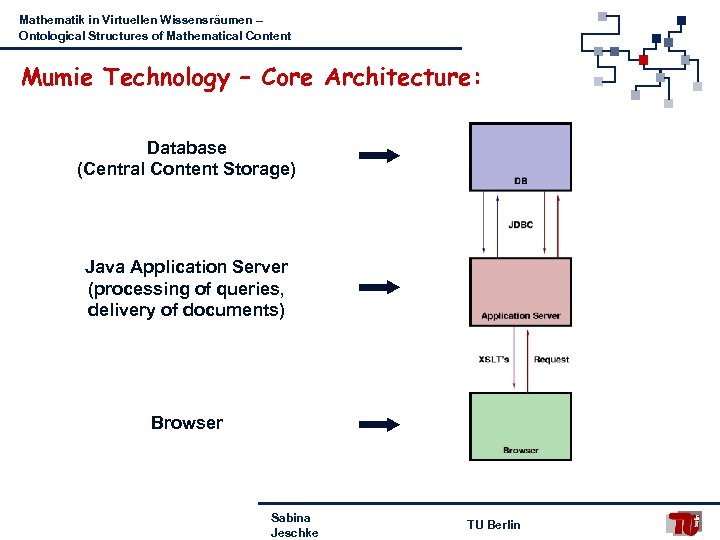Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Mumie Technology – Core Architecture: Database (Central Content Storage) Java Application Server (processing of queries, delivery of documents) Browser Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Part C: Structures of Mathematical Content Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content We need a high degree of contentual structuring: Contentual structuring of fields of knowledge „Ontology“ • • Sabina Jeschke Formal (~ machine-readable) description of the logical structure of a field of knowledge Standardised terminology Integrates objects AND their interrelation Based on objectifiable (eg logical) structures „Explicit“ specification is a basic requirement Ideally: A model of the „natural“ structure independent of use and user preference Ideally: A model independent of subjective or individual views TU Berlin

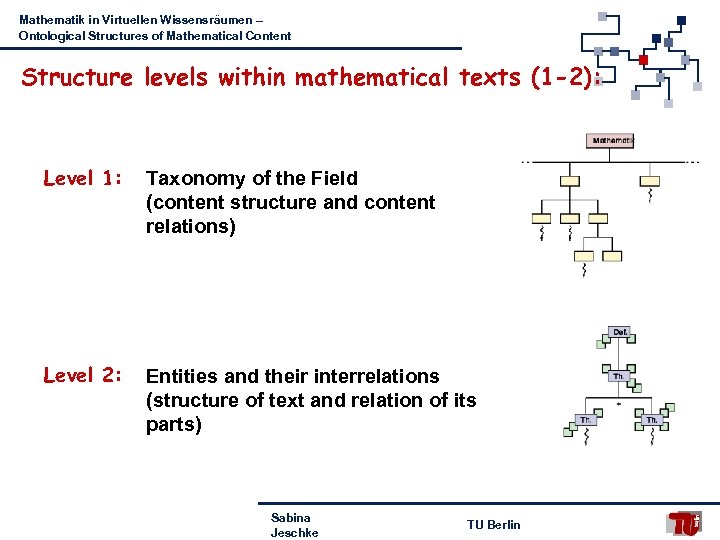Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structure levels within mathematical texts (1 -2): Level 1: Taxonomy of the Field (content structure and content relations) Level 2: Entities and their interrelations (structure of text and relation of its parts) Sabina Jeschke TU Berlin

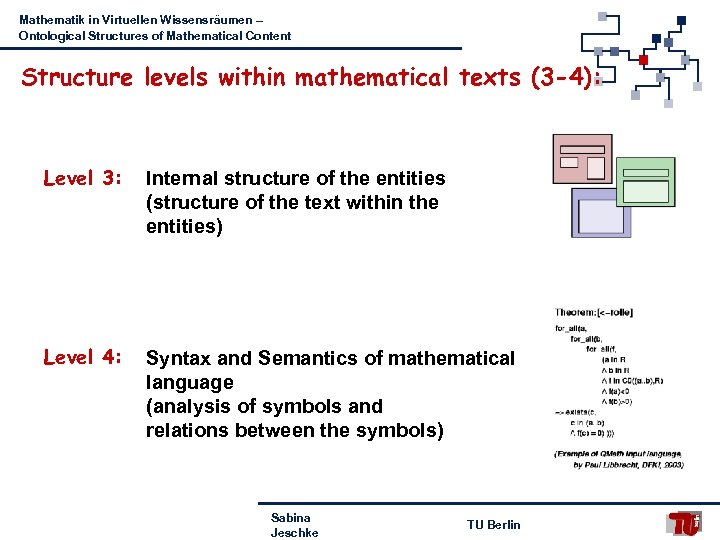Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structure levels within mathematical texts (3 -4): Level 3: Internal structure of the entities (structure of the text within the entities) Level 4: Syntax and Semantics of mathematical language (analysis of symbols and relations between the symbols) Sabina Jeschke TU Berlin

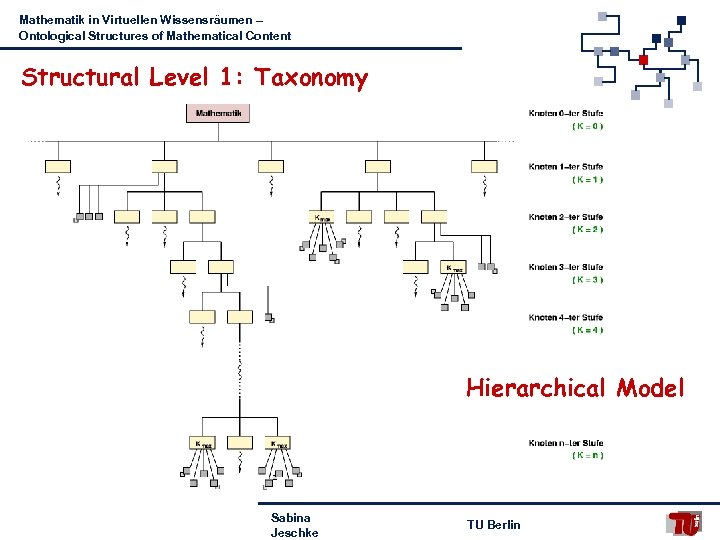Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural Level 1: Taxonomy Hierarchical Model Sabina Jeschke TU Berlin

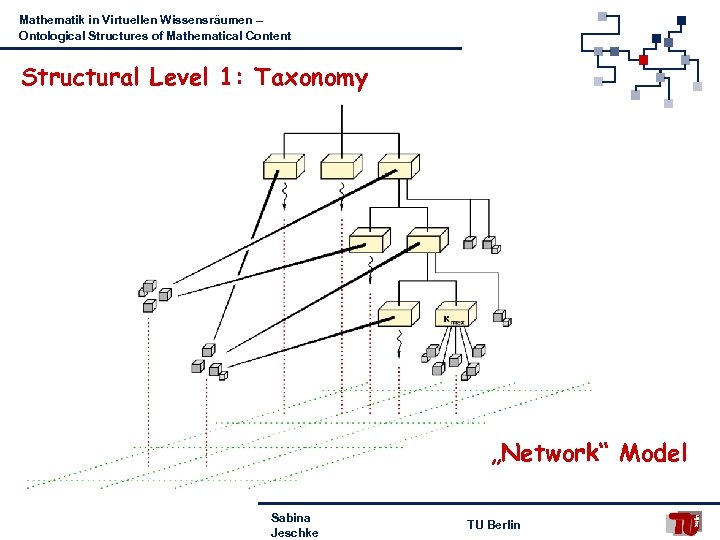Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural Level 1: Taxonomy „Network“ Model Sabina Jeschke TU Berlin

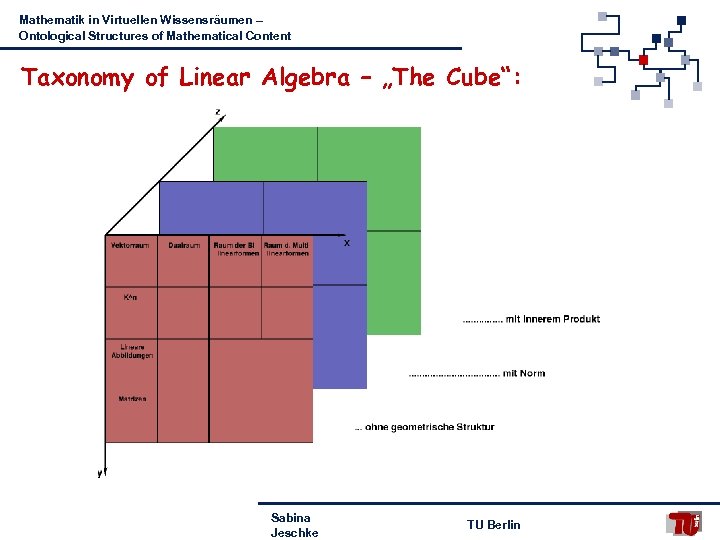Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Taxonomy of Linear Algebra – „The Cube“: hu Sabina Jeschke TU Berlin

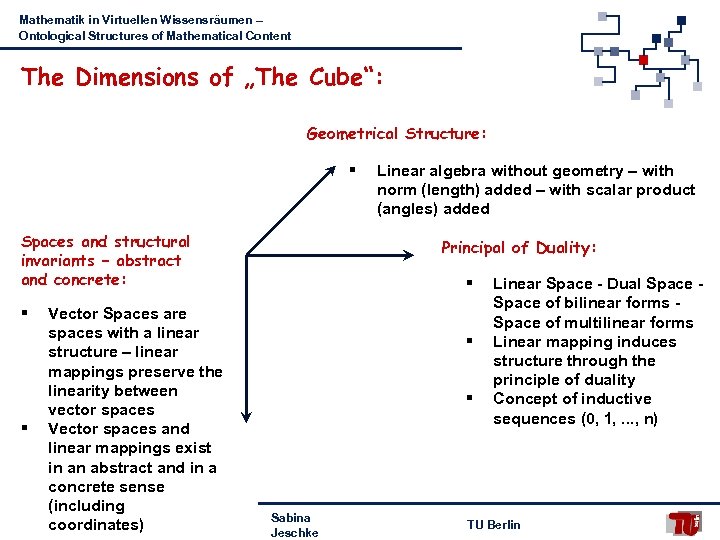Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content The Dimensions of „The Cube“: Geometrical Structure: § Spaces and structural invariants – abstract and concrete: § § Vector Spaces are spaces with a linear structure – linear mappings preserve the linearity between vector spaces Vector spaces and linear mappings exist in an abstract and in a concrete sense (including coordinates) Linear algebra without geometry – with norm (length) added – with scalar product (angles) added Principal of Duality: § § § Sabina Jeschke Linear Space - Dual Space of bilinear forms Space of multilinear forms Linear mapping induces structure through the principle of duality Concept of inductive sequences (0, 1, . . . , n) TU Berlin

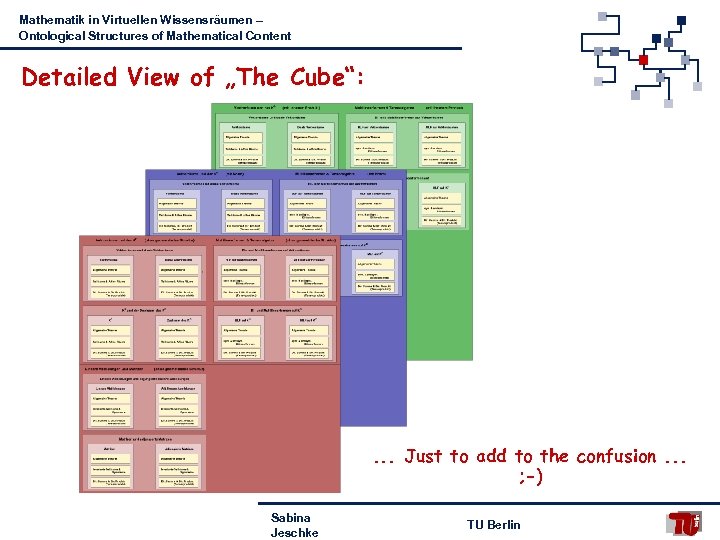Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Detailed View of „The Cube“: . . . Just to add to the confusion. . . ; -) Sabina Jeschke TU Berlin

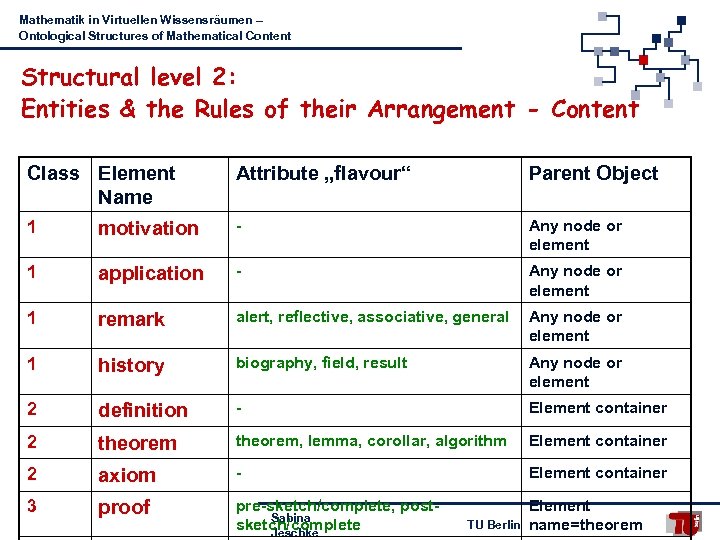Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural level 2: Entities & the Rules of their Arrangement - Content Class Element Name Attribute „flavour“ Parent Object 1 motivation - Any node or element 1 application - Any node or element 1 remark alert, reflective, associative, general Any node or element 1 history biography, field, result Any node or element 2 definition - Element container 2 theorem, lemma, corollar, algorithm Element container 2 axiom - Element container 3 proof pre-sketch/complete, post. Sabina sketch/complete Jeschke Element name=theorem TU Berlin

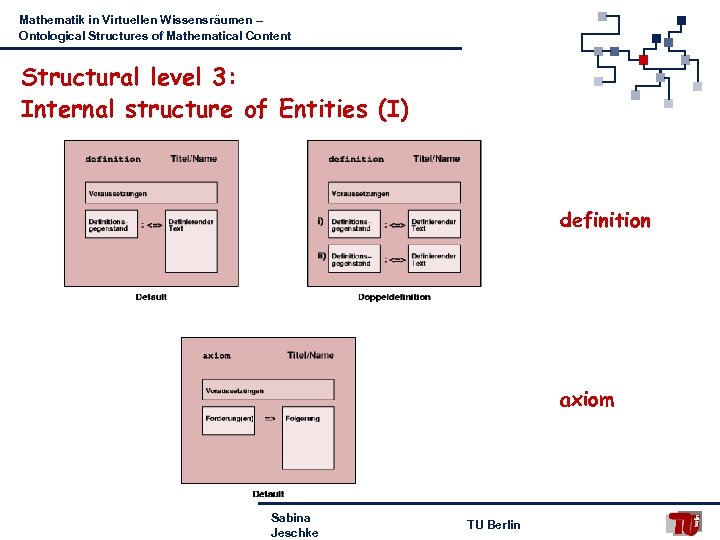Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural level 3: Internal structure of Entities (I) definition axiom Sabina Jeschke TU Berlin

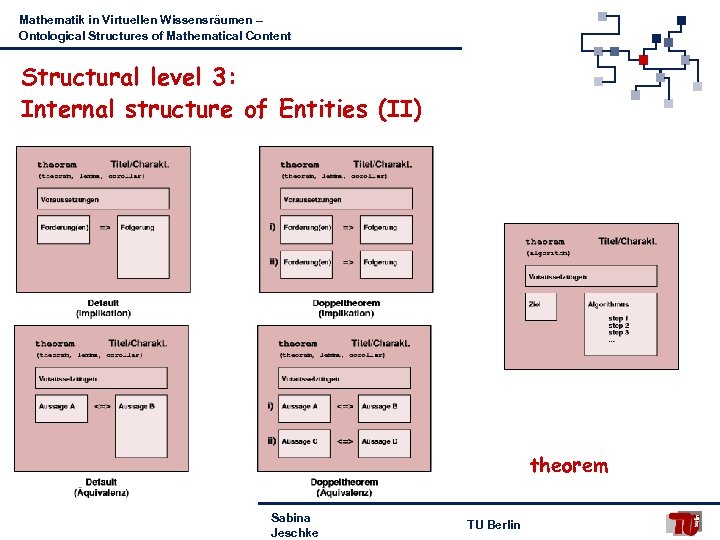Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural level 3: Internal structure of Entities (II) theorem Sabina Jeschke TU Berlin

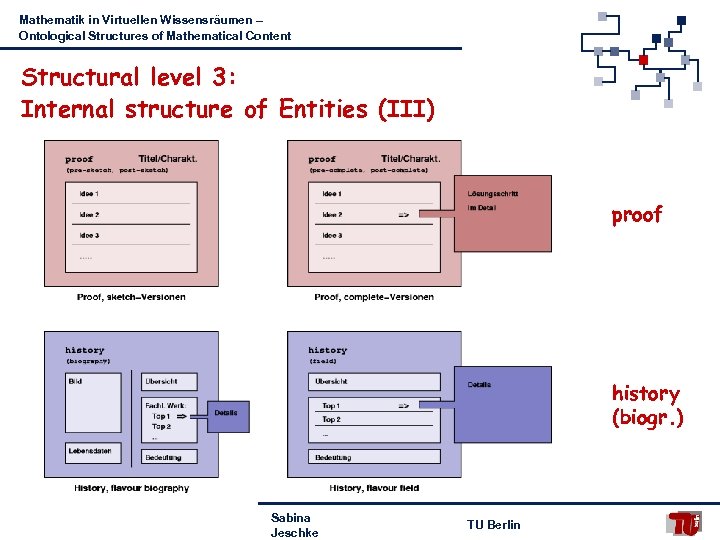Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural level 3: Internal structure of Entities (III) proof history (biogr. ) Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Structural level 3: Internal structure of Entities (IV) No internal structure provided for the following elements: • motivation • application • remark • history (field, result) • demonstration Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Part D: Next Steps - Vision Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content From Mumie. . . to Multiverse!! Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Multiverse – Idee, Programm, Ziele: Enhancement of existing projects Development of next-generation technology Integration of existing separate applications Enhancement for research applications Support of cooperative research • Internationalisization of education • Transparency of education in Europe Sabina Jeschke TU Berlin

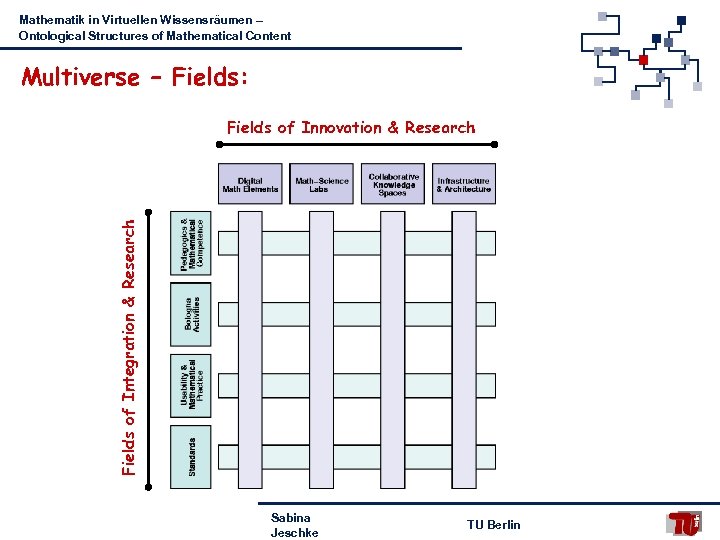Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content Multiverse – Fields: Fields of Integration & Research Fields of Innovation & Research Sabina Jeschke TU Berlin

Mathematik in Virtuellen Wissensräumen – Ontological Structures of Mathematical Content The End! Sabina Jeschke TU Berlin