592caea794381f8a55a770ec57d3343c.ppt
- Количество слайдов: 52

Mathematics and Numeracy File Final version Written by the Mathematics Department and Numeracy group Prior permission required for use outwith John Ogilvie High School, SLC. © 1

Introduction Curriculum for Excellence has given the opportunity for all educators to work together. All teachers now have a responsibility for promoting the development of Numeracy. With an increased emphasis upon Numeracy for all young people, teachers will need to revisit and consolidate Numeracy skills throughout schooling. To this end I feel that it is important that “we” (all staff at John Ogilvie High School) deliver a consistent approach to “our” pupils. Pupils always have difficulties with transferable skills and if we can deliver consistent approaches of Numeracy across the school we will be helping our pupils become successful learners. This information booklet has been produced to inform parents/carers and teachers how the Numeracy Outcomes from Curriculum for Excellence are taught within the Maths Department at John Ogilvie High School. It is hoped that use of the information in the booklet will help our parents/carers. You will hopefully be given an insight into the way number topics are being taught to your children in the school, making it easier for you to help them with their homework, and as a result improve their progress. I would like to take this opportunity to thank the maths staff, the Numeracy Group, office staff, parents and pupils from John Ogilvie High School for their contribution in producing this booklet Carol Mc. Aninch Principal Teacher of Mathematics John Ogilvie High School 2

Contents • • • 1. Estimation and Rounding 2. Number and number processes 3. Fractions 4. Decimal Fractions 5. Percentages 6. Money 7. Time 8. Measure 9. Data and analysis (graphs) 10. Probability 11. Algebra 12. Which calculator to buy? 3

1. Estimation and Rounding • Before rounding we must take the context of the question into account. The information below is a guideline. • Round 8∙ 573, a) To the nearest whole number Ans: 9, the number 5 is after the decimal point so round up b) To one decimal place Ans: 8∙ 6, the number 7 is after one decimal place so round up So ‘ 5 or above round up’ c) To two decimal places, the number 3 is after the second decimal place so we do not round up Ans: 8∙ 57 4

2. Number and Number Processes Some questions can be completed as read: • 4– 2+6 Ans: 8 • 12 ÷ 3 x ½ = 4 x ½ Ans: 2 However, To answer the questions below pupils would use an order of operations: Calculate 5 + 6 x 2 Brackets /Powers Divide/Multiply Addition/Subtraction Answer Multiply comes first, 6 x 2 = 12 then 5 + 12= 17 5

3. Fractions 6

Multiplying and dividing fractions 7

4. Decimal fractions • • Definition A fraction which has a denominator of 10 or 1000 or. . . For example 3/10; 34/100; 5/100 are decimal fractions and these are written as the decimal numbers 0. 3, 0. 34, 0. 05 respectively, whereas 0. 5 would mean 5/10 • • Some examples: Example 1 2∙ 5 + 0∙ 587 + 4∙ 63 • • Example 2 Example 3 Example 4 Example 5 Working 2∙ 500 0∙ 587 + 4∙ 630 7∙ 717 Important to add in extra zeros!!! 0∙ 53 x 5000 = 0∙ 53 x 1000 x 5 = 530 x 5 = 2650 48 ÷ 6000 = 48 ÷ 6 ÷ 1000 = 8 ÷ 1000 = 0∙ 008 2∙ 4 ÷ 0∙ 006 = 2400 ÷ 6 (multiplying both numbers by 1000) = 400 0∙ 004 x 0∙ 7 We know that 4 x 7 = 28. There are four digits after the decimal point in the question. There should be four digits after the decimal point in the answer, so the answer is 0∙ 0028. 8

5. Percentages-Calculator • Calculate 23% of £ 184. Note: Do not use percentage key on calculator. • Ans: • On calculator, 23 ÷ 100 x 184 = £ 42∙ 32 • In jotter, 23 x 184 = £ 42∙ 32 100 9

5. Percentages-Non calculator Pupils must remember: 50% = ½ 25% = ¼ 75% = ¾ 10% = 33 % = 20% = Pupils will use fractions when no calculators are allowed. 10

Multiples of 10 a) 10% of 80 =8 b) 20% of 34 Divide by 10 Divide by 5 Ans: 34 ÷ 5 = 6∙ 8 OR Ans: Find 10% of 34 = 3∙ 4 20% of 34 2 3∙ 4 = 6∙ 8 2 lots of 10% 11

Another example: 30% of 32 Ans: Find 10% of 32 = 3∙ 2 30% = 10% x 3 So 30% of 32 3∙ 2× 3 = 9∙ 6 12

Fractions and Percentages a) Find 25% of 84 Ans: ¼ of 84 Divide by 4 = 21 b) Find 75% of 120 Ans: ¾of 120 = 90 Divide by 4 then multiply your answer by 3 13

More examples 1) Find 15% of 260 Ans: Find 10% of 260 = 26 5 % of 260 = 13 5% is half of 10% So 15% = 10% + 5% = 26 + 13 = 39 14

2. 35% of 120 3. 23% of 260 Note: 20% can also be calculated using Ans: Find 10% of 120 = 120 ÷ 10 =12 30% of 120 3× 12 = 36 5% of 120 =6 So 35% = 36 + 6 = 42 30% = 10% x 3 Ans: Find 10% of 260 = 26 20% of 260 2× 26 = 52 1% = 260 ÷ 100 = 2∙ 6 3% = 2∙ 6 x 3 = 7∙ 8 So 23% = 52 + 7· 8 = 59· 8 15

7. Money Best Buys Pupils are encouraged to use unit amounts (i. e. find the value of 1) to decide which is the better value for money. Example 1 The same brand of coffee is sold in two different sized jars as shown. Which jar represents the better value for money? Find the cost per gram for both jars. 100 g costs 186 p so 186 ÷ 100 = 1. 86 p per gram. 250 g costs 247 p so 247 ÷ 250 = 0. 988 p per gram. Since the large jar costs less per gram it is better value for money. Wages and Salaries Pupils will have to learn that people earn money in all sorts of ways, e. g. hourly, weekly, monthly or yearly (salary). Remember: 52 weeks per year, 12 months in a year and “annual” means yearly. Example 1 Isobel gets paid £ 19760 per annum. What is her weekly wage? £ 19760 ÷ 52 = £ 380 Example 2 a) Duncan is a chef. His wage last week was £ 249 for working 30 hours. Calculate his hourly rate of pay? Hourly rate = £ 249 ÷ 30 = £ 8. 30 b) This week he worked 38 hours. How much did he earn? This week he earned 38 X £ 8. 30 = £ 315. 40 16

Overtime In some jobs the rate of pay is higher for people working at night, weekends or holidays. Double time is the normal rate X 2 Time and a half is the normal rate X 1. 5 Example 1 Stuart is a long distance lorry driver with a basic wage of £ 14. 50 per hour. His overtime pay is paid at double time. Calculate what he gets for 7 hours overtime. Overtime = 7 X (2 X £ 14. 50) = £ 203 Example 2 Janet works in a petrol station, getting £ 6 per hour. Her overtime rate is time and a half. Calculate her total pay for a week in which she works 34 hours plus 5 hours overtime. Basic wage = 34 X 6 = £ 204 Overtime = 5 X (1. 5 X £ 6) = £ 45 Total pay = £ 204 + £ 45 = £ 249 Commission Some people, particularly salespersons, receive a lower basic wage, but boost their earnings by adding on a percentage of their total sales – this is called commission. Example 1 Sally sells kitchens. She earns 13% commission on each kitchen she sells. How much is she paid for selling a £ 3000 kitchen. Commission = 13% of £ 3000 = 13 ÷ 100 X 3000 = £ 390 17

Hire Purchase is a way of paying for a product over a period of time. This is useful as people can get a product and pay it off over time. Hire purchase works as follows: A deposit is paid and the product can be taken by the customer. The customer pays weekly or monthly instalments until the product is fully paid. When an item is bought through hire purchase, it usually ends up costing more than it would have if the product was paid for outright. This extra money is sometimes called interest. Example 1 The cash price for a sofa is £ 1100. To pay for the sofa through hire purchase a 15% deposit has to be paid then twelve monthly instalments of £ 90. a) How much will the deposit be? Deposit = 15% of £ 1100 = 15÷ 100 X 1100 = £ 165 b) How much would be paid for all 12 instalments? Instalments = 12 X £ 90 = £ 1080 c) What is the total hire purchase price of the sofa? HP Price = £ 165 + £ 1080 = £ 1245 d) How much more is than the cash price? Interest = £ 1245 - £ 1100 = £ 145 18

Foreign Exchange The rate of exchange for each currency will normally be given by an amount per £ and it changes daily with the stock market. Great Britain uses the pound (GBP) as its currency. Many European countries use the euro. Foreign Money = Number of Pounds X Exchange Rate Number of Pounds = Foreign Money ÷ Exchange Rate In May 2010 the exchange rate was: £ 1 1. 15€ Example 1 Robert goes on holiday to Paris and takes £ 600 spending money with him. Using the exchange rate above how many euros would he get? Euros = 600 X 1. 15 = 690€ Example 2 Jim returns from a school trip to Germany with 85€. Use the exchange rate above to find out how many pounds he will get back. Pounds = 85 ÷ 1. 15 = £ 73. 91 Gross Pay, Net Pay and Deductions Gross pay is the amount that an employer pays you. Deductions are taken from your gross pay and include things like: Superannuation – a type of extra pension for when you retire. National Insurance (NI) – to pay for loss of earnings if you are sick / unemployed. Income Tax – paid to the government to pay for education, health, transport etc. Net pay is the amount that you take home after deductions are made. Net Pay = Gross pay – Deductions Example 1 Blair has a gross pay of £ 26000 per annum. He pays £ 4892 in deductions. a) b) Calculate his annual net pay. Net pay = £ 26000 - £ 4892 = £ 21108 Calculate his monthly take home pay. Monthly pay = £ 21108 ÷ 12 = £ 1759 19

Income Tax Income tax calculation is a difficult and sometimes very confusing process. The Inland Revenue (H. M. R. C. ) do not calculate your bill purely on your gross income. Instead they give you allowances and relief on part of your income. The allowances change after we have a budget. Taxable Income = Gross Pay – Allowances. Value Added Tax (VAT) The government also raises money by charging V. A. T. Most items that you purchase include VAT (usually at 20%). Example 1 Find the total cost of a car costing £ 7800 + VAT. Vat Total = = = 20% of £ 7800 20 ÷ 100 X 7800 £ 1560 £ 7800 + £ 1560 £ 9360 Three quick methods. To find VAT only X 0. 20 or 0. 2 To find the price including the VAT X 1. 20 To find the price without VAT ÷ 1. 20

Insurance Questions on insurance usually involve you reading values from tables and performing calculations. There are many different types of insurance: People take out Building Insurance policies to protect themselves against fire damage, storm damage, burst pipes etc. Household Content cover protects us from e. g. theft or accidental damage to the living room carpet. The payment made each year is called a P Premium and Insurance Companies usually quote the cost of insuring contents for each £ 1000 of value. Some people take out Life Insurance policies (Whole Life) so that when they die their loved ones are left with some money. There is also endowment policy scheme where people place savings to earn interest and take out the money later in life. If you drive, you are required by law to have your car insured in case of accident or theft. The cost of your motor insurance depends on: The make of your car and engine size. Where you live Your age A No Claims Discount is money deducted from your annual premium the longer you are able to drive without making a claim. People are obliged to take out Travel Insurance mainly to cover against their holiday being cancelled or delayed, their luggage being lost on the journey or to pay for medical attention if they take ill while on holiday. The cost of your insurance depends on where you are going and for how long. Children under 12 years normally pay 50% less and under 3’s go free. 21

7. Time Convert between 12 hour and 24 hour clock 12. 00 am 0000 hours 1. 32 pm 1332 hours 11. 42 pm 2342 hours *If a question is given in 24 hour clock time the answer must also be given 24 hour clock time and vice versa. Time intervals Question How long did the film last? Answer Start 1. 40 pm Finish 3. 15 pm 1. 40 pm to 2 pm = 20 minutes 2 pm to 3. 15 pm = 1 hour 15 minutes Total 1 hour 35 minutes 22

Converting hours and minutes to decimal hours The most common mistake made by pupils is converting 2 hours 30 minutes to 2∙ 3 hrs and thinking 0∙ 1 hour is 10 minutes. It is very important to highlight common errors to pupils. Pupils should be aware of the basics: 15 mins changes to 0∙ 25 hours 30 mins to 0∙ 5 hours 45 mins to 0∙ 75 hours To change 1 hour 23 minutes in a calculator: 23÷ 60 = 0∙ 383 (to 3 decimal places) so 1∙ 383 hours. If this conversion was part of a speed, distance and time question it is best to round to 3 decimal places to avoid losing any accuracy. To change 1. 2 in a calculator: 0∙ 2 x 60 = 12 minutes. Answer 1 hour 12 minutes • Examples of calculating speed, distance and time will follow: Learning the triangle below is an easy way to remember all 3 formulas: 23

Speed Calculate the average speed of a plane which travels a distance of 343 km in 2 hours 30 minutes. 2 hr 30 min = 2∙ 5 hrs 24

Distance Calculate to one decimal place, the distance travelled in 1 hour 37 minutes at an average speed of 58 miles per hour. Convert to decimal hours 37 ÷ 60 = 0∙ 617 d=sxt d = 58 x 1· 617 d = 93· 8 miles 25

Time Calculate, in hours and minutes, the time taken to travel 56 km at 24 km/hr. 0∙ 33˙ x 60 = 20 mins 26

7. Measure Commonly used units of measure: Length 10 mm = 1 cm 1000 m = 1 km 100 cm = 1000 mm = 1 mile = 1∙ 609 kms (to 3 decimal places) Mass (Weight) 1000 g = 1 kg 1000 kg = 1 tonne Volume 1000 ml = 1 litre 1 cm³ = 1 ml 1000 litres = 1 m³ 10 ml = 1 cl (centilitre) 1000 cm³= 1 litre 27

9. Data and analysis Using the average to Compare Data The average (or mean) of a set of scores is found by • Adding all the scores together • Then dividing by the number of scores In any example you do, pupils should always show they added the set of numbers first, then show their division. Example Find the mean of the four numbers, 5, 6, 2 and 7 Mean = 5 + 6 + 2 +7 = 20 = 5 4 4 28

Types of data A graph is a pictorial representation of a set of data. When you plan to collect data, one of the first things to think about is what kind of data you will collect as this will influence the way you organise data. Will the data be words (qualitative data) or numbers (quantitative data) ? If they are numbers, will you be counting (discrete/discontinuous data) or measuring (continuous data)? Example You are collecting data on TV programmes. The kind of programme (e. g. soap, drama, documentary) is qualitative. The length of a programme is quantitative and continuous. The number of TV programmes is quantitative and discrete/discontinuous. Some examples of graphs will follow. 29

• Checklist when drawing graphs • Bar graph • Histogram • Line Graph • Pie chart 30

Drawing graphs We expect pupils to: • • • use a sharpened pencil and ruler at all times give the graph a title label the axes with quantity and unit if it is a bar graph, to label the bars in the centre of the bar (each bar has an equal width) and make sure to leave an even space between each bar label the frequency (up the side ie vertical axes) on the lines not on the spaces if it is a line graph to plot the points neatly (using a cross or a dot) if asked to draw a line of best fit then the line should have the same number of points above the line as below it. if necessary, make use of a jagged line to show that the lower part of the graph has been missed out label all the sections or include a key when drawing a pie chart 31

Bar graphs Bar charts can be used for continuous or discrete data. They are often used to present data in a pictorial form to illustrate the information collected and highlight important points. Example The marks awarded for an assignment set for a class of 20 students were as follows: 6 7 5 7 7 8 7 6 9 7 4 10 6 8 8 9 5 6 4 8 Step 1 - Present this information in a frequency table. 32
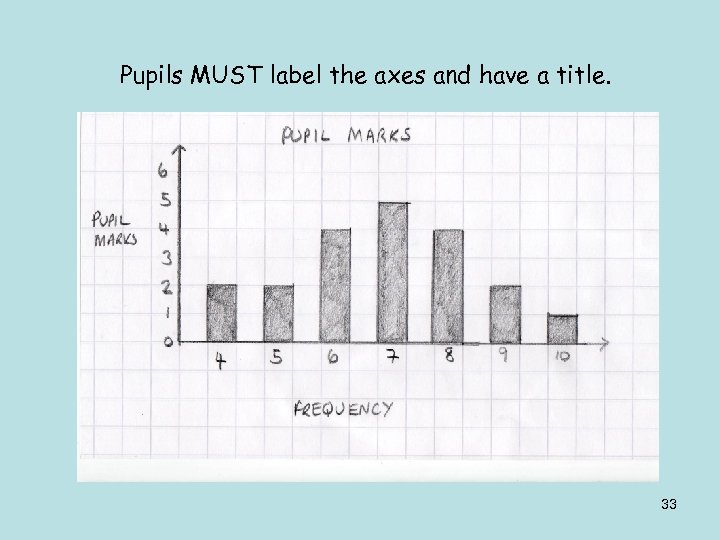
Pupils MUST label the axes and have a title. 33

Histograms are used for continuous data only. Continuous Variables: can take on unlimited number of different values e. g. time, temperature, heights and weights • • • . Lets look at the important differences between a bar graph and histogram. Bar Charts All the bars are the same width. The height or length of the bar indicates the frequency. Only one axis has a scale. Histograms For histograms bars are together as data is continuous. Bars can be different widths. Note: Histograms are usually used with grouped data. 34
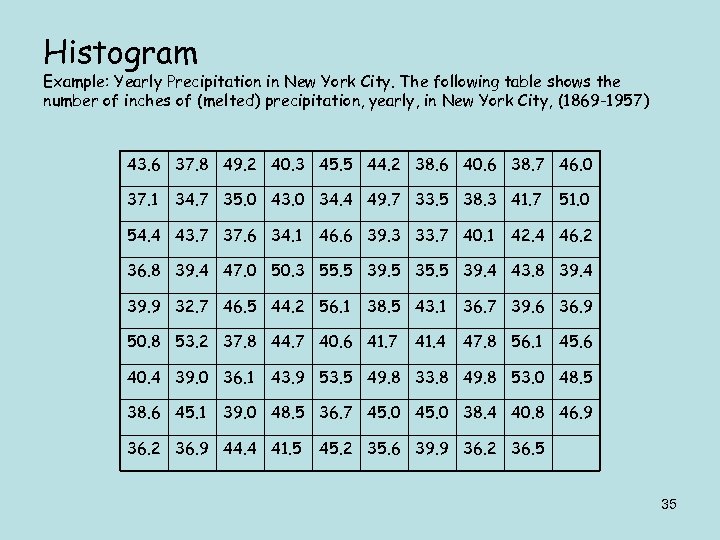
Histogram Example: Yearly Precipitation in New York City. The following table shows the number of inches of (melted) precipitation, yearly, in New York City, (1869 -1957) 43. 6 37. 8 49. 2 40. 3 45. 5 44. 2 38. 6 40. 6 38. 7 46. 0 37. 1 34. 7 35. 0 43. 0 34. 4 49. 7 33. 5 38. 3 41. 7 54. 4 43. 7 37. 6 34. 1 46. 6 39. 3 33. 7 40. 1 51. 0 42. 4 46. 2 36. 8 39. 4 47. 0 50. 3 55. 5 39. 5 35. 5 39. 4 43. 8 39. 4 39. 9 32. 7 46. 5 44. 2 56. 1 38. 5 43. 1 50. 8 53. 2 37. 8 44. 7 40. 6 41. 7 40. 4 39. 0 36. 1 38. 6 45. 1 41. 4 36. 7 39. 6 36. 9 47. 8 56. 1 45. 6 43. 9 53. 5 49. 8 33. 8 49. 8 53. 0 48. 5 39. 0 48. 5 36. 7 45. 0 38. 4 40. 8 46. 9 36. 2 36. 9 44. 4 41. 5 45. 2 35. 6 39. 9 36. 2 36. 5 35

36
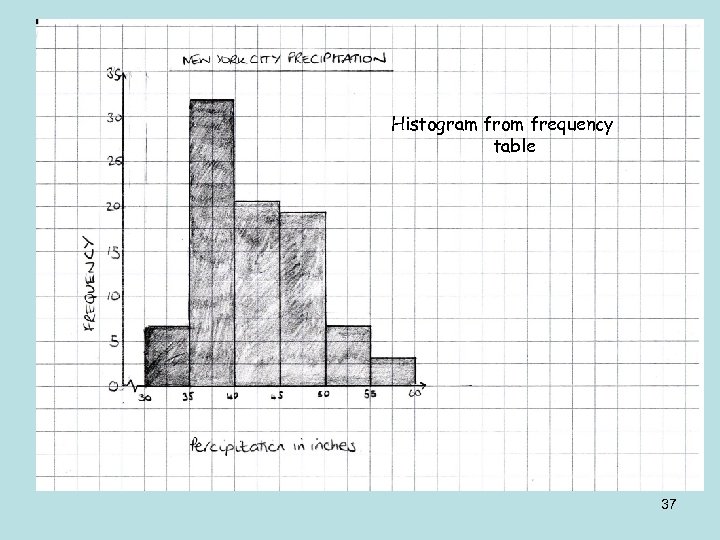
Histogram from frequency table 37

Line Graph • • • How to Manually Construct a Line Graph Obtain squared or graph paper. Identify variables Determine the range of the two variables. For each variable subtract the lowest data value from the highest data value. If you wish the origin of the graph to start at zero, use the highest data value for the range. Determine the scale of the graph. Count the number of squares horizontally and vertically on the graph paper. Divide the range of the x variable by the horizontal number of squares, then round off to the next larger convenient number. (For example, if dividing gives 34. 3, it might be convenient to allow each horizontal square to have a value of 50. ) Determine the scale for the y variable by dividing its range by the number of vertical squares, then rounding up. This procedure should spread the graph to use MOST of the available space. 38

• • • Number each axis. X-axis-Starting with a number just smaller than the smallest data value (zero if that is desired for your origin or words can be used) label each LINE along the bottom of the graph from left to right by successive multiples of the chosen scale. (For our example, 0, 50, 100, 150. . . ) It is critical that these numbers represent lines and not boxes. That will allow the space between the lines to represent values in between. Number upwards the lines along the left side of the vertical axis using the scale chosen for the y variable, starting just below the smallest data (or zero if so chosen for the origin). If lines are so close together that the numbers will be crowded, omit writing some of the numbers but continue to space as if all lines were numbered. Label each axis. – Briefly describe the properties represented by the x and y variables. – In parentheses abbreviate the measuring units used to measure the data along each axis. Plot the data points. For each pair of related data, use the value for the x variable to plot horizontal location and the value for the y variable to plot vertical location using the number lines along the axes. Make a tiny dot or mark x at the intersection of the horizontal and vertical locations to accurately show the two values. If other sets of data are also plotted on the same graph for comparison, use a different marker (square, triangle etc. ) for each set of data and use a legend box to show what each marker represents. 39

• • • Draw the line. Join dots to produce a line. Add a title. The title should be selected to clearly but briefly tell what the graph is about. Examples of line graphs are on the next page. More information: In some curricular areas an independent variable (along the x-axis) and dependent variable (y-axis) would be used to construct a scatter graph then a line of best fit would be drawn onto graph. More detailed information can be found on the internet. 40
41
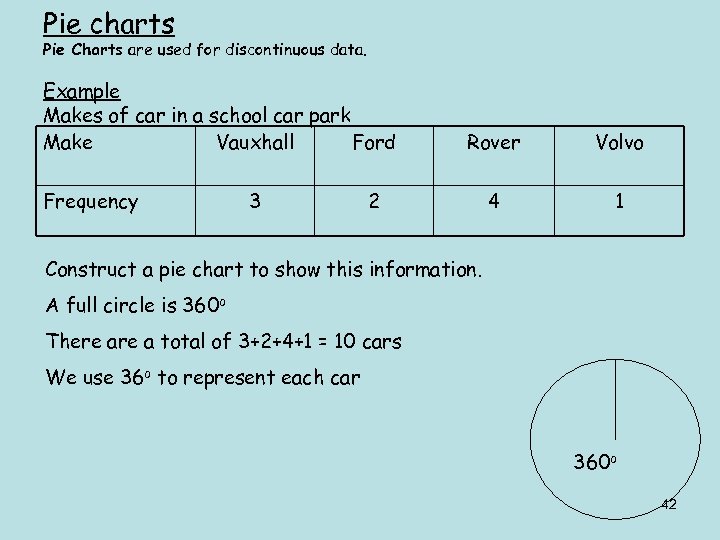
Pie charts Pie Charts are used for discontinuous data. Example Makes of car in a school car park Make Vauxhall Ford Frequency 3 Rover Volvo 4 1 2 Construct a pie chart to show this information. A full circle is 360 o There a total of 3+2+4+1 = 10 cars We use 36 o to represent each car 360 o 42

Makes of car in a school car park Make Vauxhall Ford Rover Volvo Frequency 3 2 4 1 Angle in pie chart 3 x 36 o =108 o 2 x 36 o =72 o 4 x 36 o =144 o 1 x 36 o =36 o We use 36 o to represent each car so 3 parts Vauxhall are represented by 3 x 36 o = 108 o Work out the angle needed for each of the other models of car 43
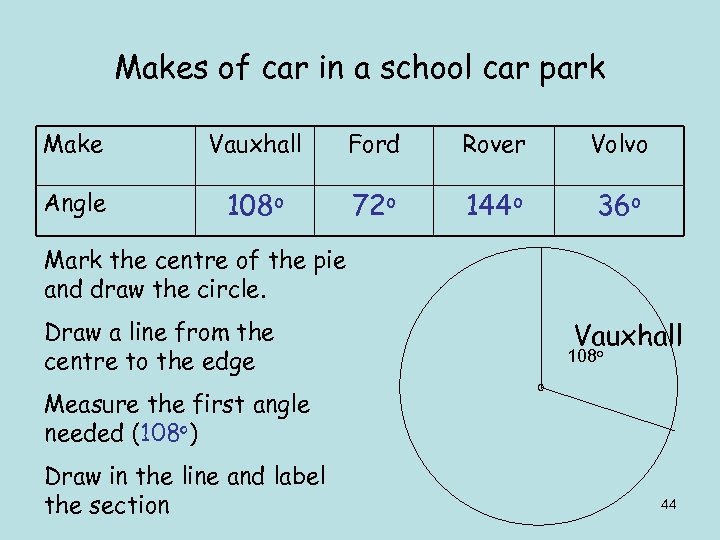
Makes of car in a school car park Make Vauxhall Ford Rover Volvo Angle 108 o 72 o 144 o 36 o Mark the centre of the pie and draw the circle. Draw a line from the centre to the edge Vauxhall o 108 Measure the first angle needed (108 o) Draw in the line and label the section 44

Makes of car in a school car park Make Vauxhall Ford Rover Volvo Angle 108 o 72 o 144 o 36 o From this line measure the next angle, draw the line and label the section. Continue in this way Check that the last section has the correct angle and label it. Volvo 36 o Vauxhall Rover 144 o 72 o Ford 45

10. Probability To find the probability of an event, we use: Probability (event) = number of favourable outcomes total number of possible outcomes An example What is the probability of picking a black counter from a bag containing five red, three blue and two black counters? Number of favourable outcomes = 2 (number of black counters) Number of possible outcomes = 5 + 3 + 2 = 10 (total number of counters) P(black) = = Always leave your fraction in its simplest form. 46
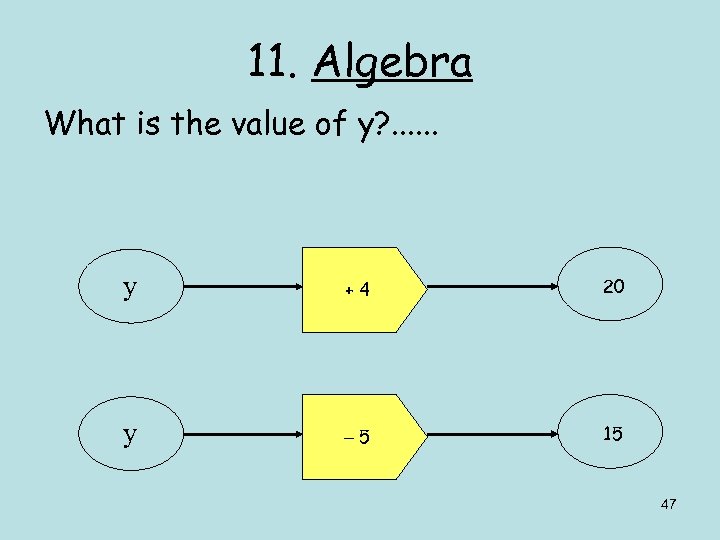
11. Algebra What is the value of y? . . . y +4 20 y 5 15 47
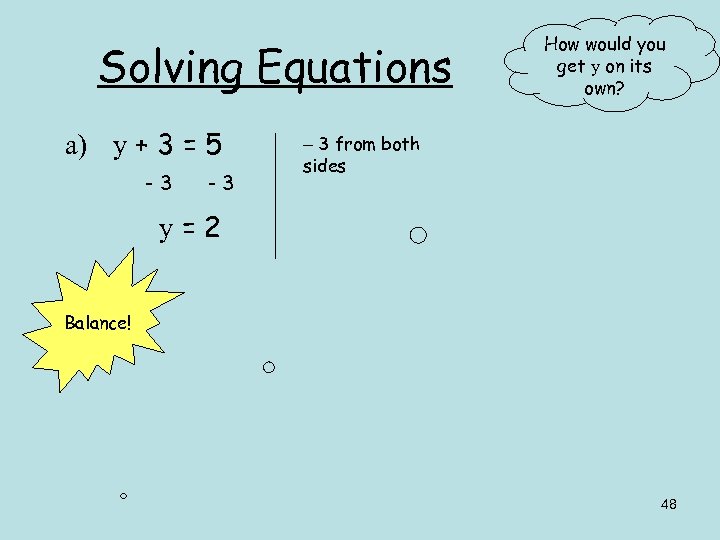
Solving Equations a) y + 3 = 5 -3 -3 How would you get y on its own? 3 from both sides y=2 Balance! 48
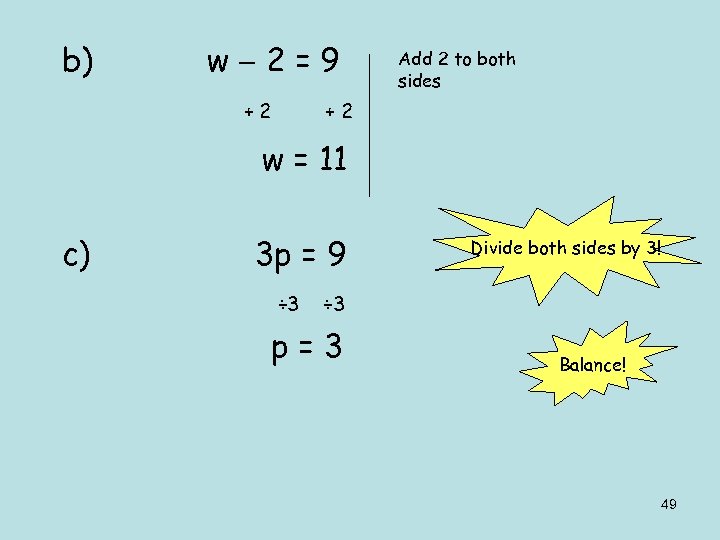
b) w 2=9 +2 Add 2 to both sides +2 w = 11 c) 3 p = 9 ÷ 3 Divide both sides by 3! ÷ 3 p=3 Balance! 49

d) 2 y + 1 = 9 -1 -1 2 y = 8 ÷ 2 Subtract 1 from both sides Divide both sides by 2 ÷ 2 y=4 e) 4 t 1 = 15 +1 Add 1 to both sides +1 4 t = 16 ÷ 4 Divide both sides by 4 ÷ 4 t=4 50

12. Which calculator to buy? In the Mathematics department we use the following calculators: Casio fx-82 MS Casio fx 83 -ES 51

The End Prior permission required for use outwith John Ogilvie High School, South Lanarkshire Council. © 52
592caea794381f8a55a770ec57d3343c.ppt