Mathematical Preliminaries 1 SETS Definition A

Mathematical Preliminaries 1

SETS • Definition: A set is well defined collection of objects, which are • • unordered distinct same type with common properties • Sets are written with curly braces {}, and the elements in the set are written within the curly braces. • The set {a, b, c} has elements a, b, and c. • The sets {a, b, c} and {b, c, b, a, a} are the same since order does not matter in a set and since redundancy does not count. • The set {a} has element a. Note that {a} and a are different things; {a} is a set with one element a.

• The set {xn : n = 1, 2, 3, . . . } consists of x, xxx, . . • The set of positive even numbers is {2, 4, 6, 8, 10, 12, . . . } = {2 n : n =1, 2, 3, . . . }. • The set of odd numbers is {1, 3, 5, 7, 9, 11, 13, . . . } = {2 n + 1 : n = 0, 1, 2, . . . }.

Set Representations C = { a, b, c, d, e, f, g, h, i, j, k } C = { a, b, …, k } finite set S = { 2, 4, 6, … } infinite set S = { j : j > 0, and j = 2 k for some k>0 } S = { j : j is nonnegative and even } Courtesy Costas Busch - RPI 4

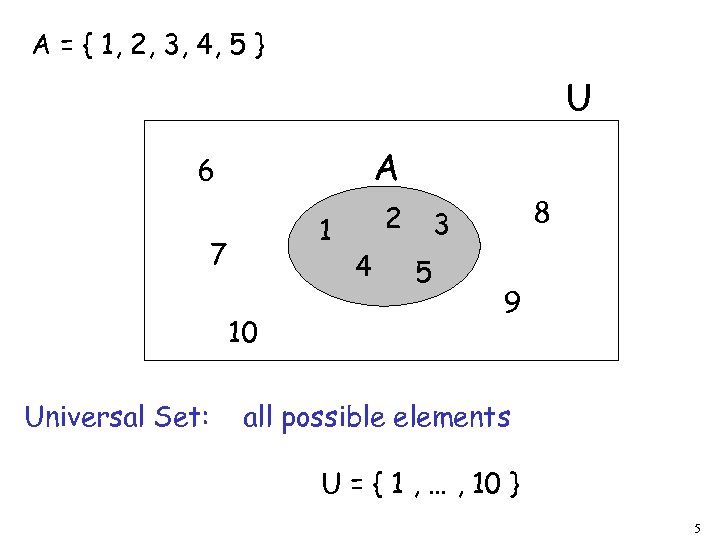A = { 1, 2, 3, 4, 5 } U A 6 1 7 10 Universal Set: 2 4 8 3 5 9 all possible elements U = { 1 , … , 10 } 5

Set Operations A = { 1, 2, 3 } B = { 2, 3, 4, 5} B A • Union A U B = { 1, 2, 3, 4, 5 } 2 3 1 4 5 • Intersection U A B = { 2, 3 } 2 3 • Difference A-B={1} 1 B - A = { 4, 5 } Venn diagrams Courtesy Costas Busch - RPI 6

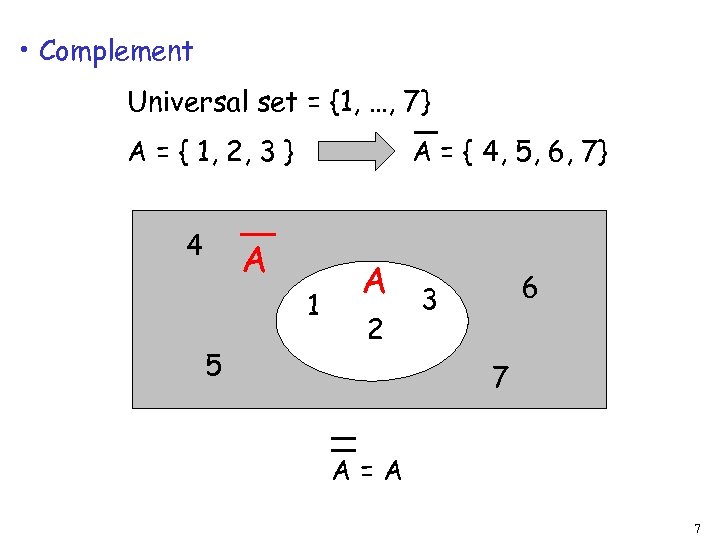• Complement Universal set = {1, …, 7} A = { 1, 2, 3 } 4 A = { 4, 5, 6, 7} A 1 5 A 2 6 3 7 A=A 7

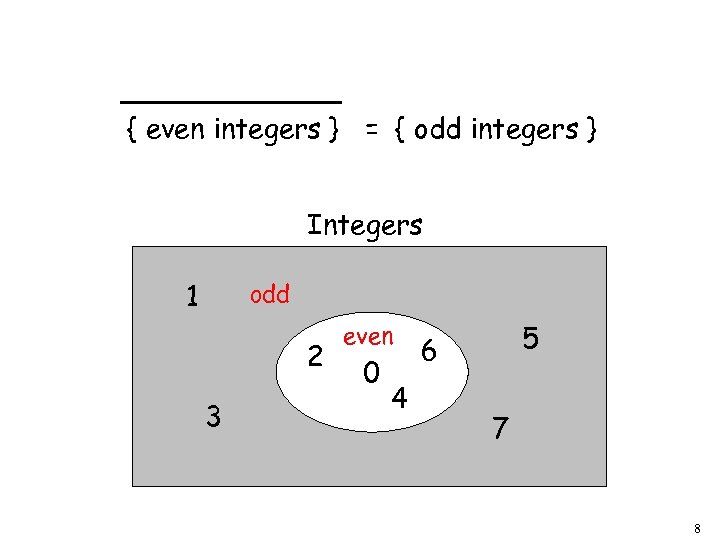{ even integers } = { odd integers } Integers 1 odd 2 3 even 0 4 5 6 7 8

De. Morgan’s Laws U AUB=A B B=AUB 9

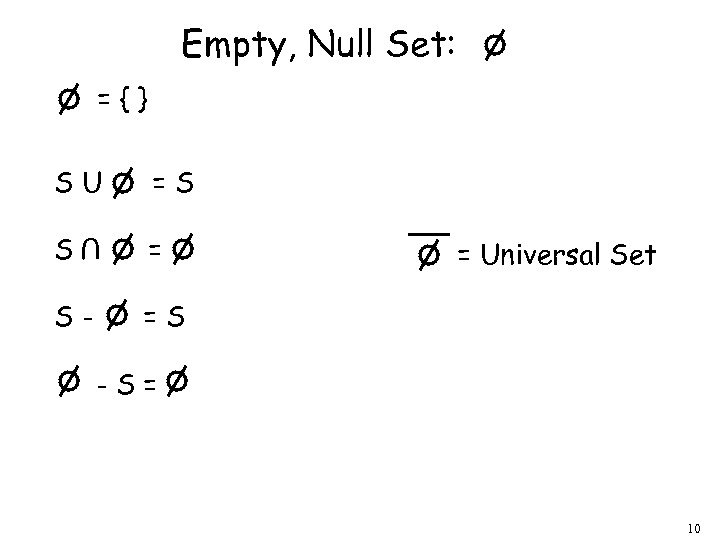Empty, Null Set: ={} SU =S S = U S- = Universal Set =S -S= 10

Subset A = { 1, 2, 3} B = { 1, 2, 3, 4, 5 } B U Proper Subset: A U A B B A 11

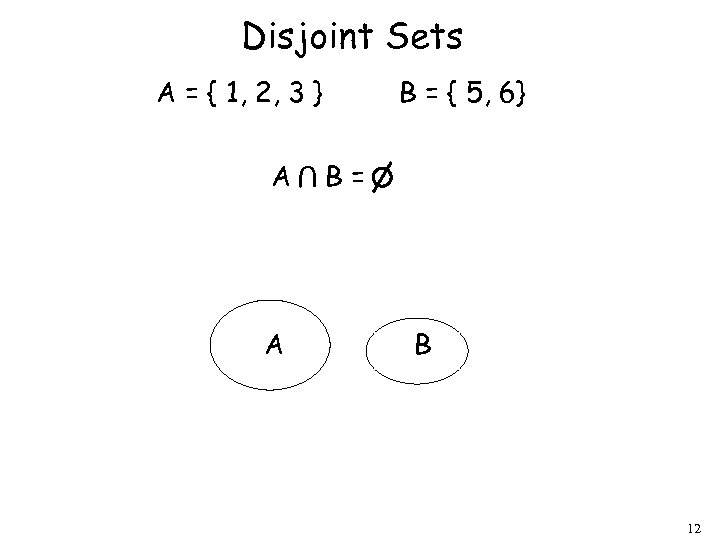Disjoint Sets A = { 1, 2, 3 } A U A B = { 5, 6} B= B 12

Set Cardinality • For finite sets A = { 2, 5, 7 } |A| = 3 (set size) 13

Powersets A powerset is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2 S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2 S | = 2|S| ( 8 = 23 ) 14

Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 5) } |A X B| = |A| |B| Generalizes to more than two sets AXBX…XZ 15

Languages 16

A language is a set of strings String: A sequence of letters Examples: “cat”, “dog”, “house”, … Defined over an alphabet: 17

Alphabets and Strings We will use small alphabets: Strings 18

String Operations Concatenation 19

Reverse 20

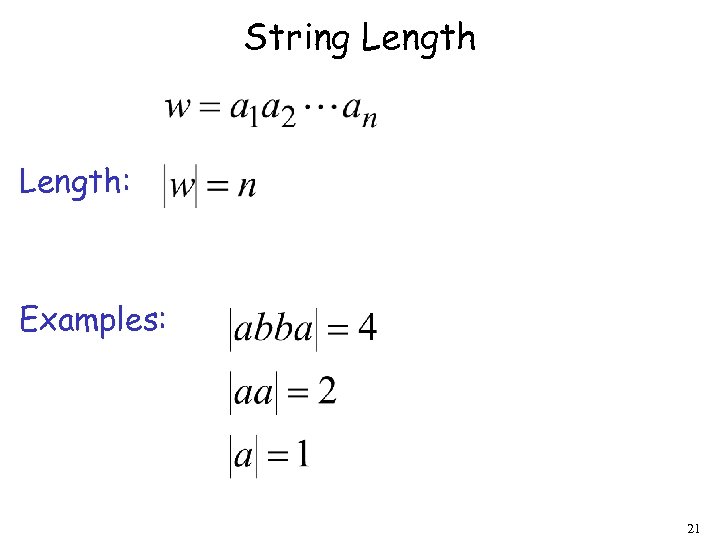String Length: Examples: 21

Length of Concatenation Example: 22

Empty String A string with no letters: Observations: 23

Substring of string: a subsequence of consecutive characters String Substring 24

Prefix and Suffix Prefixes Suffixes prefix suffix 25

Another Operation Example: Definition: 26

The * Operation : the set of all possible strings from alphabet 27

The + Operation : the set of all possible strings from alphabet except 28

Languages A language is any subset of Example: Languages: 29

Note that: Sets Set size String length 30

Another Example An infinite language 31

Operations on Languages The usual set operations Complement: 32

Reverse Definition: Examples: 33

Concatenation Definition: Example: 34

Another Operation Definition: Special case: 35

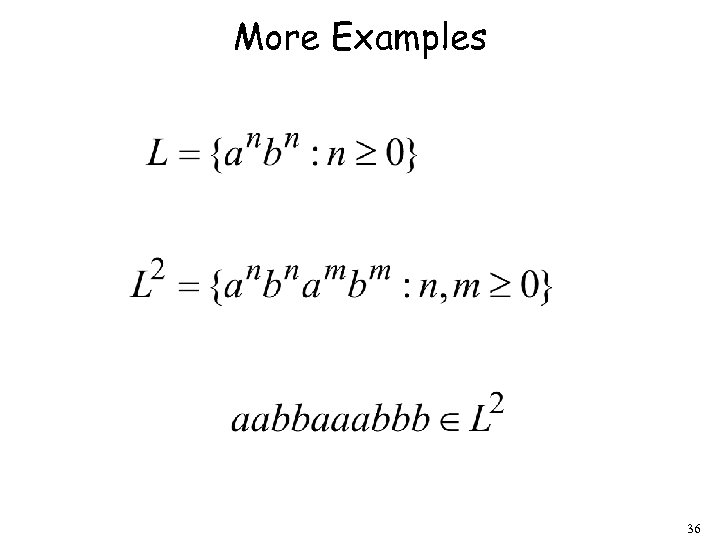More Examples 36

Star-Closure (Kleene *) Definition: Example: 37

Positive Closure Definition: 38