Mathematical Foundations of Markov Chain Monte Carlo Algorithms

Mathematical Foundations of Markov Chain Monte Carlo Algorithms Based on lectures given by Alistair Sinclair Computer Science Division U. C. Berkeley

Dana Moshkovitz Overview 1. Random Sampling 2. The Markov Chain Monte-Carlo Paradigm 3. Mixing Time 1. Coupling 2. Flow 3. Geometry Based on lectures by Alistair Sinclair. Techniques for Bounding the Mixing Time

Dana Moshkovitz Random Sampling x • • - “very large” sample set. - probability distribution over . Goal: Sample points x at random from distribution . Based on lectures by Alistair Sinclair.

Dana Moshkovitz The Probability Distribution Typically, Z=Σx w(x) is an unknown normalization factor Based on lectures by Alistair Sinclair. w: R+ is an easilycomputed weight function

Dana Moshkovitz Application 1 : Card Shuffling • • … - all 52! permutations of a deck of cards. - uniform distribution [ x w(x)=1]. Goal: pick a permutation uniformly at random Based on lectures by Alistair Sinclair.

Dana Moshkovitz Application 2 : Counting • How many ways can we tile some given pattern with dominos? Based on lectures by Alistair Sinclair.

Dana Moshkovitz Application 2 : Counting (cont(. • Sample tilings uniformly at random. • Let P 1 = proportion of sample of type 1. • Compute estimate N 1* of N 1 recursively. • output N* = N 1* / P 1. N 1 N = N 1 + N 2 sample size = O(n), #levels = O(n) O(n 2) samples total Based on lectures by Alistair Sinclair. N 2

Dana Moshkovitz Application 3 : Volume & Integration [DyerFriezeKannan] • : a convex body in Rd (d large) • Problem: estimate vol( ) sequence of concentric balls B 0 … B r estimate by sampling uniformly from Bi Generalization: Integration of log-concave function over a cube A Rd Based on lectures by Alistair Sinclair.

Dana Moshkovitz Application 4 : Statistical Physics • - set of configurations of a physical system • - Gibbs distribution • (x)=Pr[ system in config. x]=w(x)/Z • where w(x)=e-H(x)/KT “energy” Based on lectures by Alistair Sinclair. “temperature”

Dana Moshkovitz The Ising Model • n atomic magnets • configuration: x {-, +}n • H(x)= -(#aligned neighbors) - + - - + - - + Based on lectures by Alistair Sinclair. + + + - + +

Dana Moshkovitz Why Sampling ? • statistics of “typical” configurations. • mean energy (E [H(x)]), specific heat, … • estimate of “partition function” Z: =Z(T)= x w(x) Based on lectures by Alistair Sinclair.

Dana Moshkovitz Estimating the Partition Function • Let =e-1/KT Z: =Z( )= x -H(x). • Define 1= 0 < 1 < …< r=. r nlog =O(n 2) can be estimated by random sampling from i-1 i i-1(1+1/n) ensures small variance O(n) samples suffice for each ratio Based on lectures by Alistair Sinclair.

Dana Moshkovitz Application 5 : Optimization • - set of feasible solutions to an optimization problem • f(x) - value of solution x. • Goal: maximize f(x). • Idea: sample solutions where w(x)= f(x). Based on lectures by Alistair Sinclair.

Dana Moshkovitz Application 5 : Optimization • Idea: sample solutions where w(x)= f(x). large concentration on good solutions (large values f(x)) small greater “mobility” (local optima are less high) Simulated Annealing heuristic: Slowly increase … Based on lectures by Alistair Sinclair.

Dana Moshkovitz Application 6 : Hypothesis Verification in Statistical Models • - set of hypotheses • X - observed data Let w( )=P( )P(X/ ). prior Based on lectures by Alistair Sinclair. “easy”

Dana Moshkovitz Application 6 : Hypothesis Verification in Statistical Models (cont. ) Sampling from ( )=P( /X) gives: 1. Statistical estimate of hypotheses . 2. Prediction: 3. Model comparison: normalization factor = P(X) = Prob[ model generated X ] Based on lectures by Alistair Sinclair.

Dana Moshkovitz Markov Chains • Sample space • Random variables (r. v) over X 1, X 2, …, Xt, … • “Memoryless”: t>0, x 1, …, xt+1 , Based on lectures by Alistair Sinclair.

Dana Moshkovitz Sampling Algorithm • Start at an arbitrary state X 0. • Simulate MC for “sufficiently many” steps t. • Output Xt. X 0 Xt Then, x Prob[ Xt = x ] ≈ (x) Based on lectures by Alistair Sinclair.

Dana Moshkovitz Transitions Matrix • • • P is non-negative P is stochastic ( x x. P(x, y)=1) Pr[Xt+1=y/X 0=x]=Pt(x, y) Pxt=Px 0 · Pt Definition: is a stationary distribution, if P=. Based on lectures by Alistair Sinclair. y x Pr[Xt+1=y/Xt=x] Px P

Dana Moshkovitz Irreducibility Definition: P is irreducible if x Based on lectures by Alistair Sinclair. y

Dana Moshkovitz Aperiodicity Definition: P is aperiodic if Based on lectures by Alistair Sinclair.

Note on Irreducibility and Aperiodicity • If P is irreducible, we can always make it aperiodic, by adding “self-loops”: P’ = ½(P+I) • P’ has same stationary distribution as P. • Call P’ a “lazy” MC. y x Based on lectures by Alistair Sinclair. Dana Moshkovitz

Dana Moshkovitz Fundamental Theorem: If P is irreducible and aperiodic, then it is ergodic, i. e where is the (unique) stationary distribution of P – i. e P=. Based on lectures by Alistair Sinclair.

Main Idea (The MCMC Paradigm( An ergodic MC provides an effective algorithm for sampling from . Based on lectures by Alistair Sinclair. Dana Moshkovitz

Dana Moshkovitz Examples 1. 2. 3. 4. 5. Random Walks on Graphs Ehrenfest Urn Card Shuffling Coloring of a Graph The Ising Model Based on lectures by Alistair Sinclair.

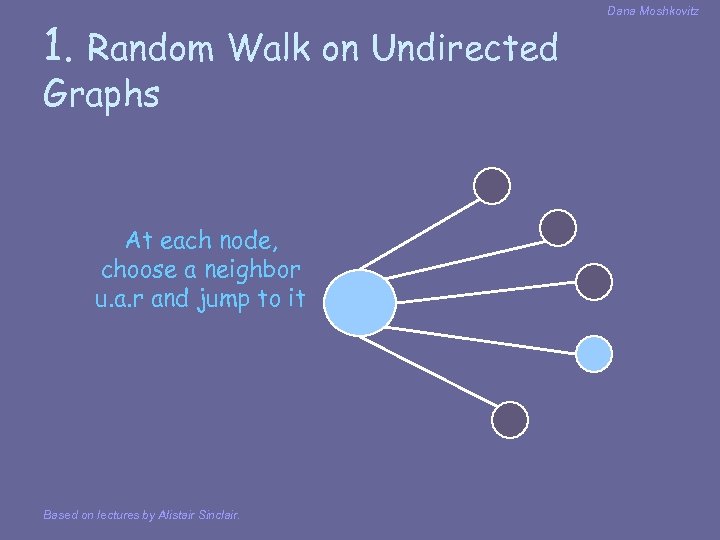1. Random Walk on Undirected Graphs At each node, choose a neighbor u. a. r and jump to it Based on lectures by Alistair Sinclair. Dana Moshkovitz

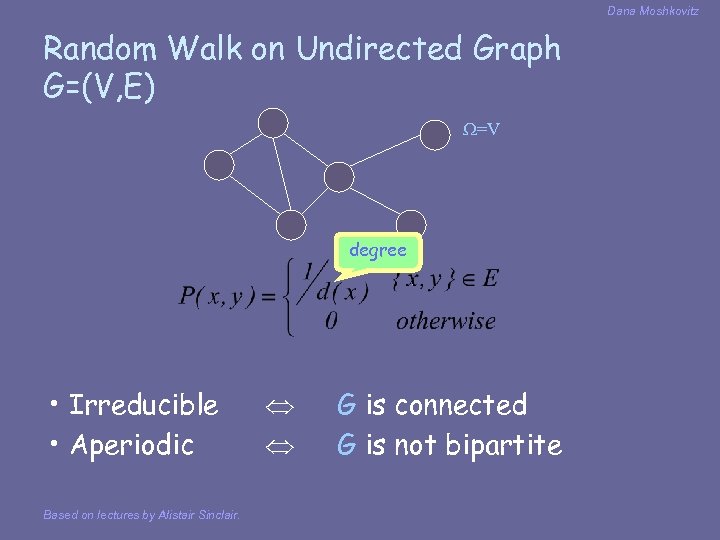Dana Moshkovitz Random Walk on Undirected Graph G=(V, E) =V degree • Irreducible • Aperiodic Based on lectures by Alistair Sinclair. G is connected G is not bipartite

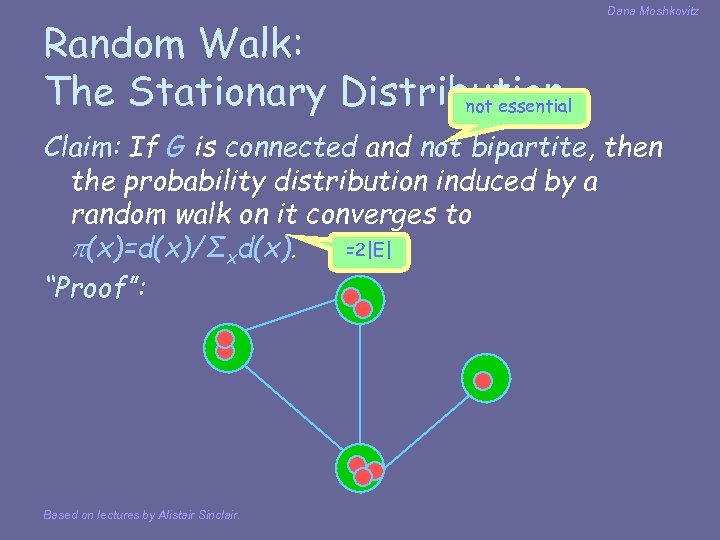Random Walk: The Stationary Distribution not essential Dana Moshkovitz Claim: If G is connected and not bipartite, then the probability distribution induced by a random walk on it converges to =2|E| (x)=d(x)/Σxd(x). “Proof”: Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 2 Ehrenfest Urn j balls (n-j) balls • Pick a ball u. a. r • Move the ball to the other urn Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 2 Ehrenfest Urn • Xt = number of balls in first urn. • MC is a non-uniform random walk on ={0, 1, …, n}. j/n 1 -j/n . . . 0 1 2 3 . . . (j-1) • Irreducible ; Periodic • Stationary distribution : Based on lectures by Alistair Sinclair. j (j+1) n

Dana Moshkovitz . 3 Card Shuffling a) Top-in-at-random § Irreducible § Aperiodic § P is doubly stochastic: y Σx. P(x, y)=1 § is uniform: x (x)=1/n! Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 3 Card Shuffling b) Random Transpositions § Irreducible § Aperiodic § P is symmetric: x, y P(x, y)=P(y, x) § is uniform Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 3 Card Shuffling c) Riffle shuffle [Gilbert/Shannon/Reeds] Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 3 Card Shuffling c) Riffle shuffle [Gilbert/Shannon/Reeds] § Irreducible § Aperiodic § P is doubly stochastic § is uniform Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 4 Colorings of a graph • • G=(V, E) : connected, undirected q : number of colors : set of proper q-colorings of G : uniform Based on lectures by Alistair Sinclair.

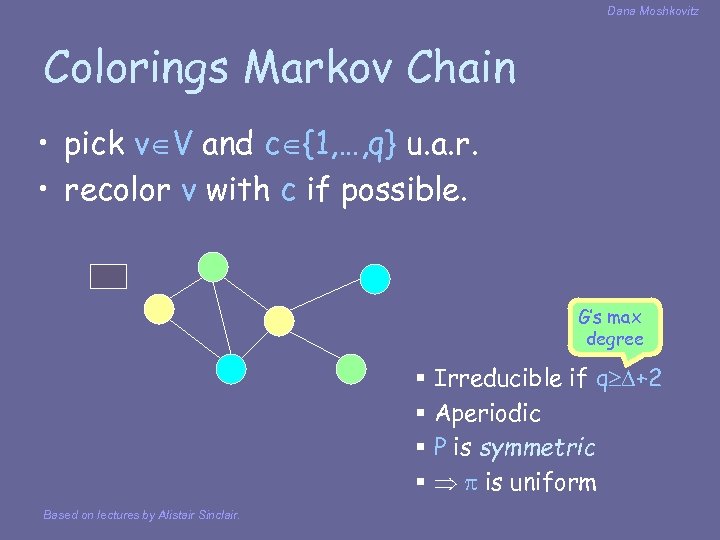Dana Moshkovitz Colorings Markov Chain • pick v V and c {1, …, q} u. a. r. • recolor v with c if possible. G’s max degree § Irreducible if q +2 § Aperiodic § P is symmetric § is uniform Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 5 The Ising Model Markov chain (“Heat bath”): • pick a site i u. a. r • replace spin x(i) by random spin x’(i) s. t • n sites • ={-, +}n • w(x)= #{aligned neighbors (x)} - + - - + - - + #{+ neighbors of i} + + + - + + Irreducible, aperiodic, reversible w. r. t converges to Based on lectures by Alistair Sinclair.

Dana Moshkovitz Designing Markov Chains What do we want? • Given , • MC over which converges to Based on lectures by Alistair Sinclair.

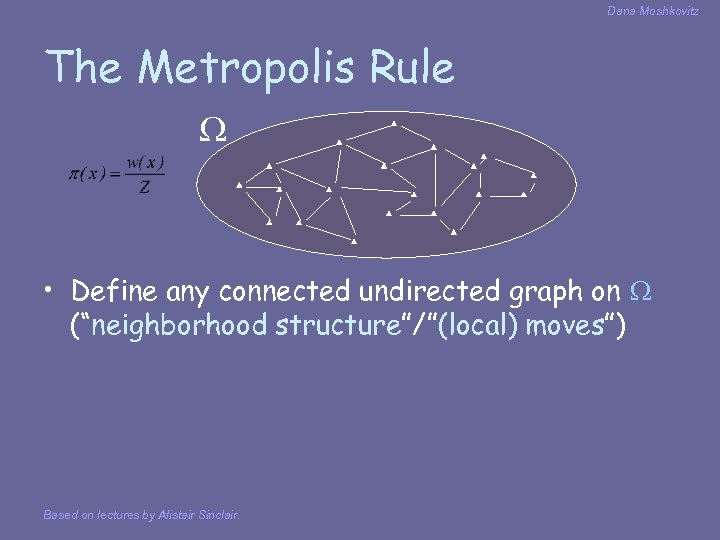Dana Moshkovitz The Metropolis Rule • Define any connected undirected graph on (“neighborhood structure”/”(local) moves”) Based on lectures by Alistair Sinclair.

Dana Moshkovitz The Metropolis Rule • Transitions from state x : – pick a neighbor y of x w. p (x, y) – move to y w. p min{w(y)/w(x), 1} (x, y)= (y, x), (x, x)=1 -Σy-x (x, y) (else stay at x) Based on lectures by Alistair Sinclair. § Irreducible § Aperiodic (make lazy if nec. ) § reversible w. r. t w § converges to .

Dana Moshkovitz The Mixing Time Key Question: How long until Pxt looks like ? We will use the variation distance: Based on lectures by Alistair Sinclair.

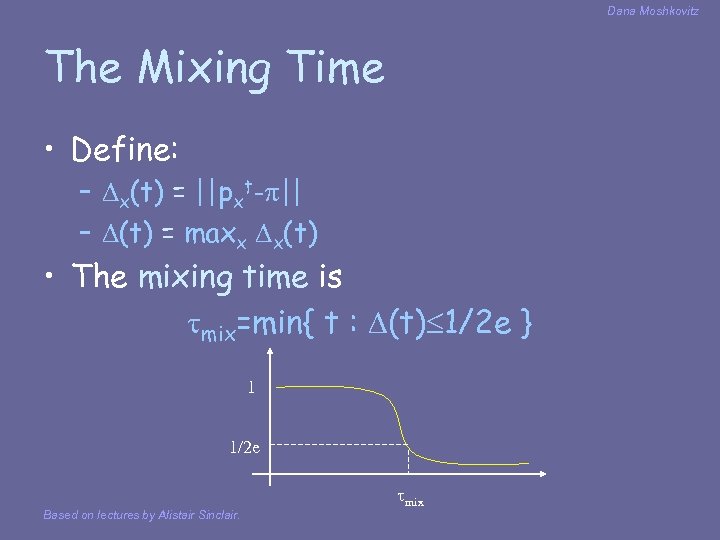Dana Moshkovitz The Mixing Time • Define: – x(t) = ||pxt- || – (t) = maxx x(t) • The mixing time is mix=min{ t : (t) 1/2 e } 1 1/2 e mix Based on lectures by Alistair Sinclair.

Dana Moshkovitz Toy Example: Top-In-At-Random • Let T = time after initial bottom card reaches top • T is a strong stationary time, i. e Pr[Xt=x/t=T]= (x) • Claim: (t) Pr[T>t] • Thus, it remains to estimate T. n Based on lectures by Alistair Sinclair.

Dana Moshkovitz The Coupon Collector Problem • Each pack contains one coupon. • The goal is to complete the series. • How many packs would we buy? ! Based on lectures by Alistair Sinclair.

Dana Moshkovitz The Coupon Collector Problem • N – total number of different coupons. • Xi – time to get the i-th coupon. Based on lectures by Alistair Sinclair.

Dana Moshkovitz Toy Example: Top-In-At-Random • By the coupon collector, – the i-th coupon is a ‘ticket’ to advance from the (n-i+1) level to the next one. • Pr[ T > nlnn + cn] e-c • mix=nlnn + cn n Based on lectures by Alistair Sinclair.

Dana Moshkovitz Example: Riffle Shuffle Based on lectures by Alistair Sinclair.

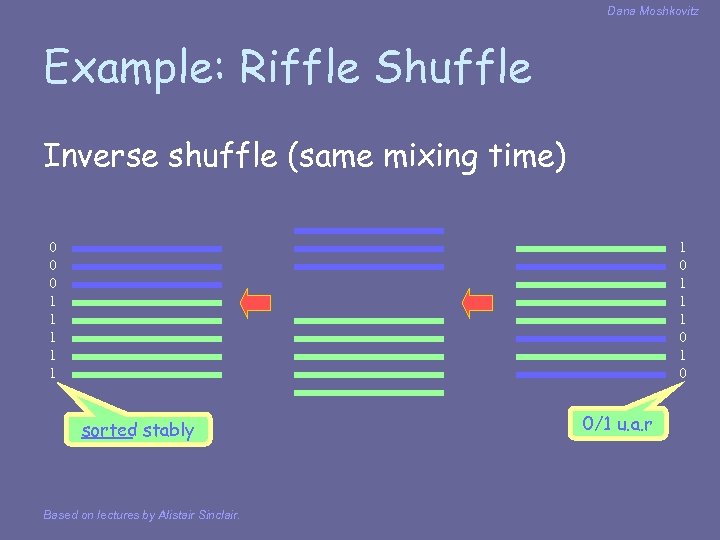Dana Moshkovitz Example: Riffle Shuffle Inverse shuffle (same mixing time) 0 0 0 1 1 1 0 sorted stably Based on lectures by Alistair Sinclair. 0/1 u. a. r

Dana Moshkovitz Inverse Shuffle • After t steps, each card is labeled with t digits. • Cards are sorted by their labels. • Cards with different labels are in random order • Cards with same label are in original order Based on lectures by Alistair Sinclair. 000 001 010 011 100 101 111

Dana Moshkovitz Riffle Shuffle (Cont(. • Let T = time until all cards have distinct labels • T is a strong stationary time. • Again we need to estimate T. Based on lectures by Alistair Sinclair.

Dana Moshkovitz B i rthday Paradox • With which probability two of them have the same birthday? Based on lectures by Alistair Sinclair.

Dana Moshkovitz B I rthday Paradox (Cont(. • k people, n days (n>k>1) • The probability all birthdays are distinct: arithmetic sum Based on lectures by Alistair Sinclair.

Dana Moshkovitz Riffle Shuffle (Cont(. • By the birthday paradox, – each card (1. . n) picks a random label – there are 2 t possible labels – we want all labels to be distinct • mix=O(logn) Based on lectures by Alistair Sinclair.

Dana Moshkovitz General Techniques for Mixing Time • Probabilistic • Combinatorial • Geometric Based on lectures by Alistair Sinclair. – “Coupling” – “Flows” - “Conductance”

Dana Moshkovitz Coupling Based on lectures by Alistair Sinclair.

Dana Moshkovitz Mixing Time Via Coupling Let P be an ergodic MC. A coupling for P is a pair process (Xt, Yt) s. t • Xt, Yt are each copies of P • Xt=Yt Xt+1=Yt+1 Define Txy=mint {Xt=Yt | X 0=x, Y 0=Y} Based on lectures by Alistair Sinclair.

Dana Moshkovitz Coupling Theorem [Aldous et al. ]: (t) maxx, y. Pr[Tx, y > t] Design a coupling that brings X and Y together fast Based on lectures by Alistair Sinclair.

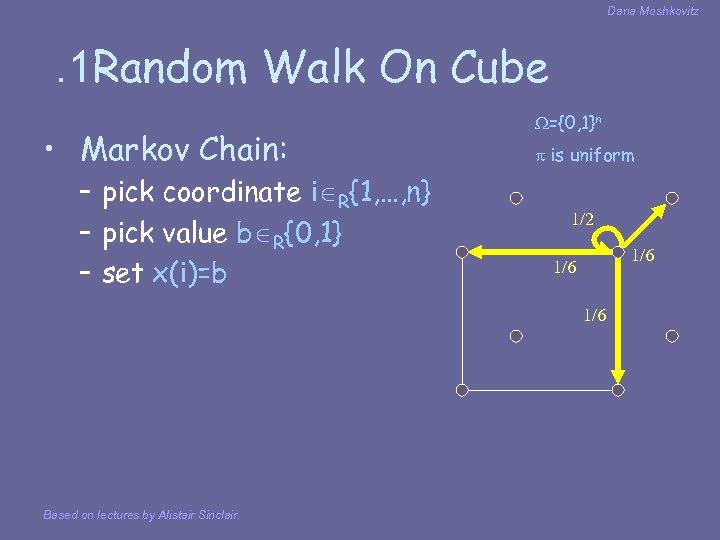Dana Moshkovitz . 1 Random Walk On Cube • Markov Chain: – pick coordinate i R{1, …, n} – pick value b R{0, 1} – set x(i)=b ={0, 1}n is uniform 1/2 1/6 1/6 Based on lectures by Alistair Sinclair.

Dana Moshkovitz Coupling For Random Walk • pick same i, b for both X and Y (0, 0, 1, 1) (1, 1, 0, 0, 1, 0) 1 • Txy time to hit all n coordinates • By coupon collecting, Pr[ Txy > nlnn + cn ] < e-c • mix nlnn + cn Based on lectures by Alistair Sinclair.

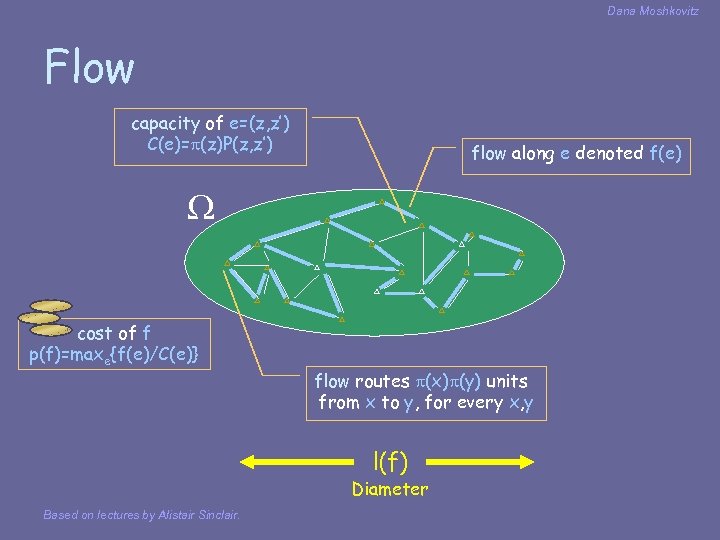Dana Moshkovitz Flow capacity of e=(z, z’) C(e)= (z)P(z, z’) flow along e denoted f(e) cost of f p(f)=maxe{f(e)/C(e)} flow routes (x) (y) units from x to y, for every x, y l(f) Diameter Based on lectures by Alistair Sinclair.

Dana Moshkovitz Flow Theorem [Diaconis/Stroak, Jerrum/Sinclair]: For a lazy ergodic MC and any flow f, x( ) 2·p(f)·l(f)·[ ln (x)-1 + 2 ln -1 ] Based on lectures by Alistair Sinclair.

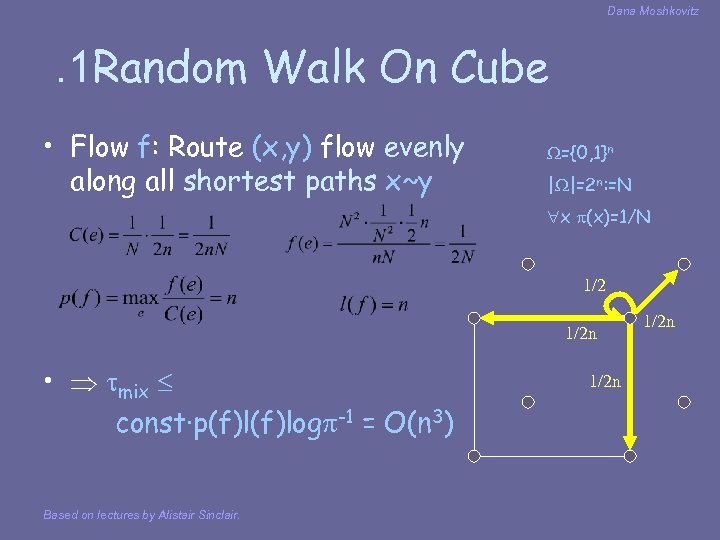Dana Moshkovitz . 1 Random Walk On Cube • Flow f: Route (x, y) flow evenly along all shortest paths x~y ={0, 1}n | |=2 n: =N x (x)=1/N 1/2 n • mix const·p(f)log -1 = O(n 3) Based on lectures by Alistair Sinclair. 1/2 n

Dana Moshkovitz Conductance “bottlen e ck” Based on lectures by Alistair Sinclair.

Dana Moshkovitz Conductance S Based on lectures by Alistair Sinclair. - S

Dana Moshkovitz Conductance Theorem [Jerrum/Sinclair, Lawler/Sokal, Alon, Cheeger…]: For a lazy reversible MC, x( ) 2/ 2·[ ln (x)-1 + ln -1 ] Based on lectures by Alistair Sinclair.

Dana Moshkovitz . 1 Random Walk On Cube • The sketched S is (essentially) the worst S. • mix = O( -2 ·log min-1) = O(n 3) Based on lectures by Alistair Sinclair.