Math Teacher Kozhahmetov Kuat Definition Space geometry

Math Teacher: Kozhahmetov Kuat

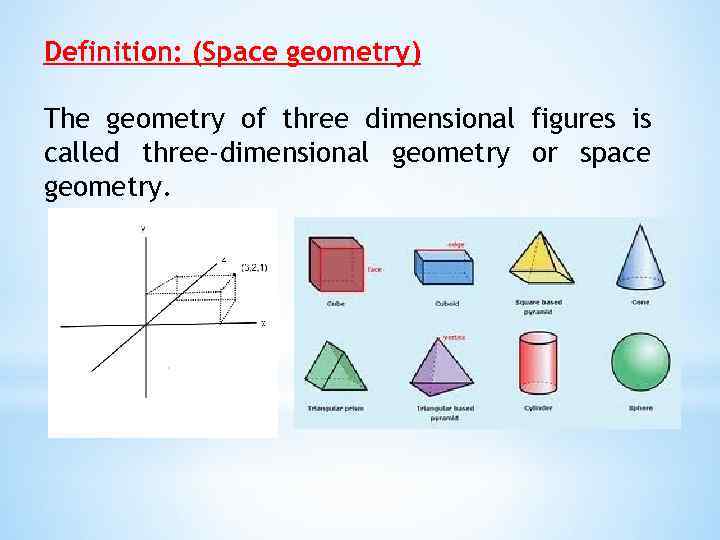Definition: (Space geometry) The geometry of three dimensional figures is called three-dimensional geometry or space geometry.

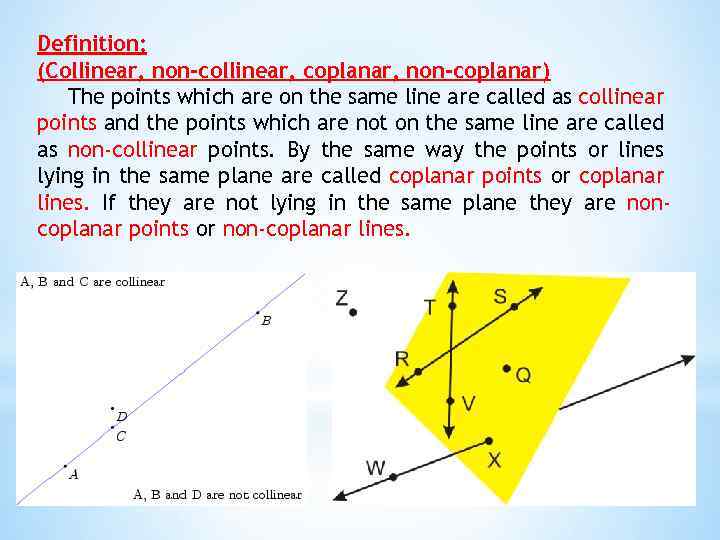Definition: (Collinear, non-collinear, coplanar, non-coplanar) The points which are on the same line are called as collinear points and the points which are not on the same line are called as non-collinear points. By the same way the points or lines lying in the same plane are called coplanar points or coplanar lines. If they are not lying in the same plane they are noncoplanar points or non-coplanar lines.

Axioms of Space Geometry 1. Two different points in space determine a line.

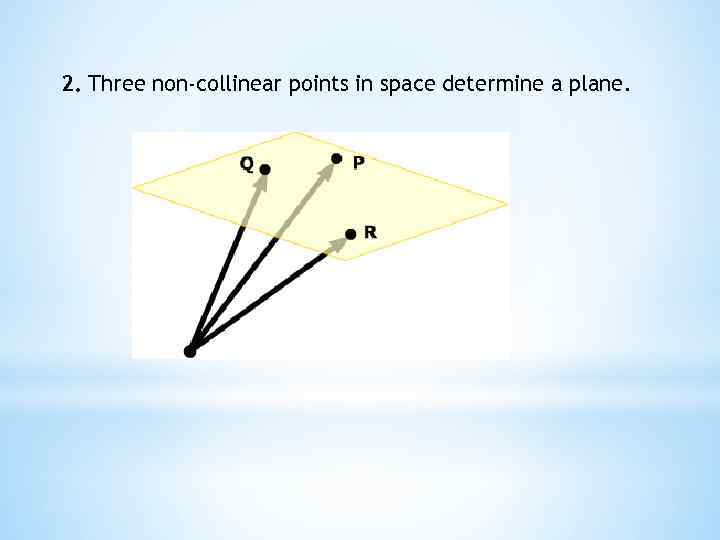2. Three non-collinear points in space determine a plane.

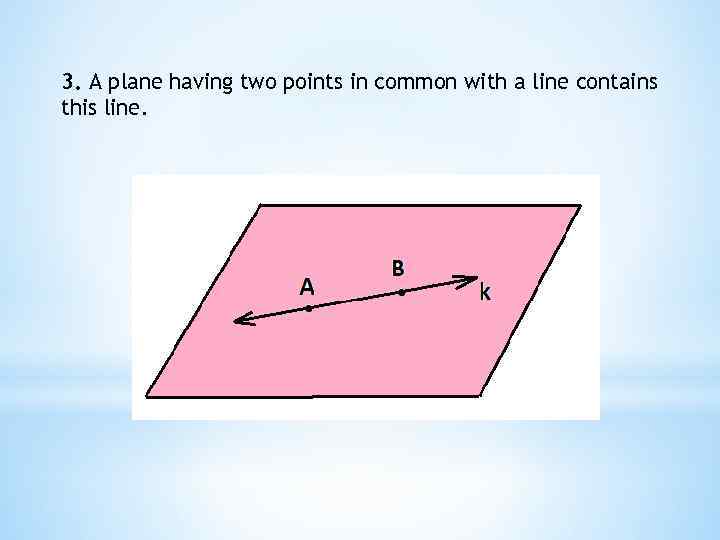3. A plane having two points in common with a line contains this line.

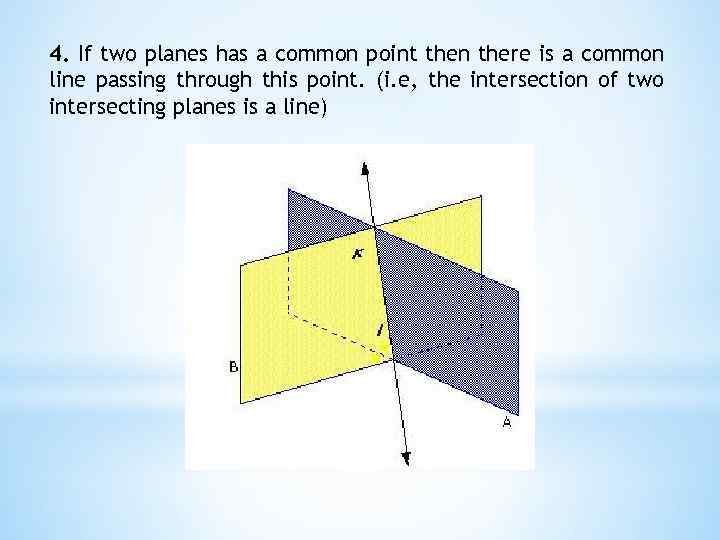4. If two planes has a common point then there is a common line passing through this point. (i. e, the intersection of two intersecting planes is a line)

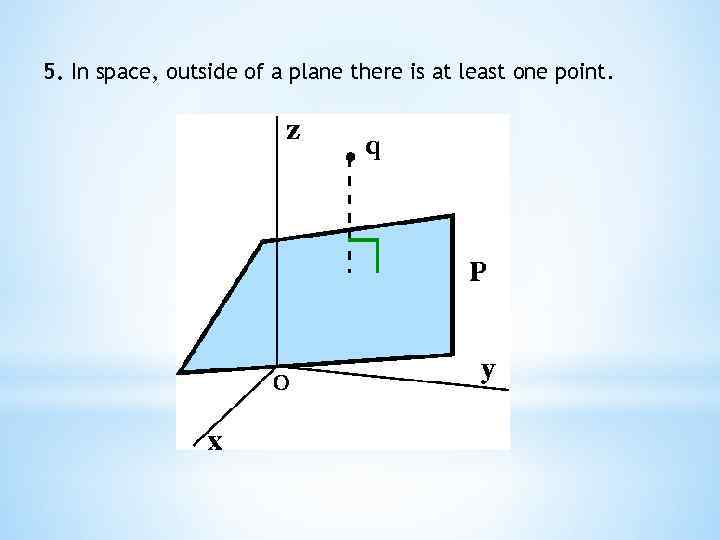5. In space, outside of a plane there is at least one point.

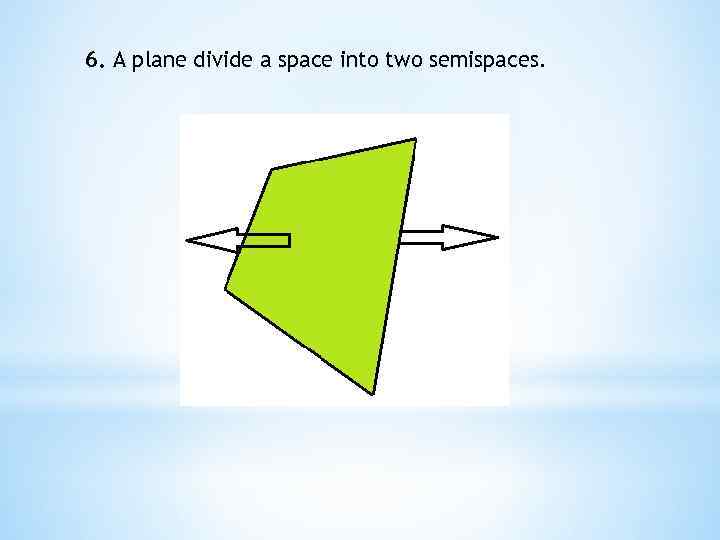6. A plane divide a space into two semispaces.

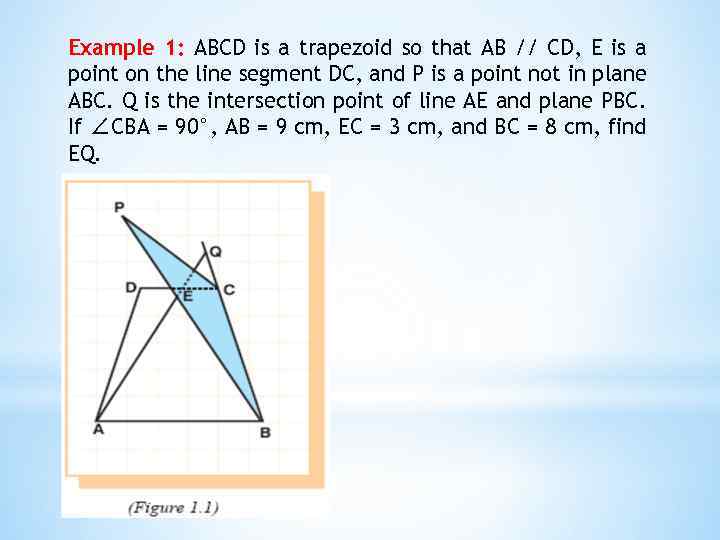Example 1: ABCD is a trapezoid so that AB // CD, E is a point on the line segment DC, and P is a point not in plane ABC. Q is the intersection point of line AE and plane PBC. If ∠CBA = 90°, AB = 9 cm, EC = 3 cm, and BC = 8 cm, find EQ.

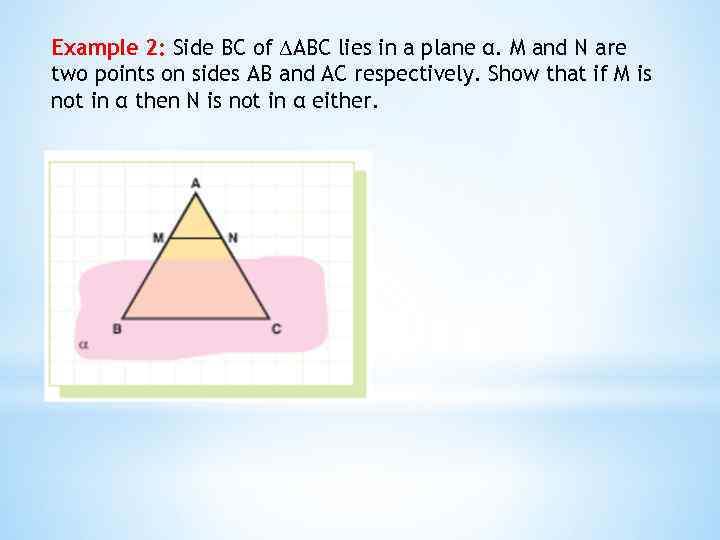Example 2: Side BC of ABC lies in a plane α. M and N are two points on sides AB and AC respectively. Show that if M is not in α then N is not in α either.

*