64cddca24b683568ef636ea36ae6e274.ppt
- Количество слайдов: 116
 Math Calculations For HERS Raters 1
Math Calculations For HERS Raters 1
 Why Worry 2
Why Worry 2
 Why Worry 3
Why Worry 3
 Why Worry 4
Why Worry 4
 Calculating Areas 5
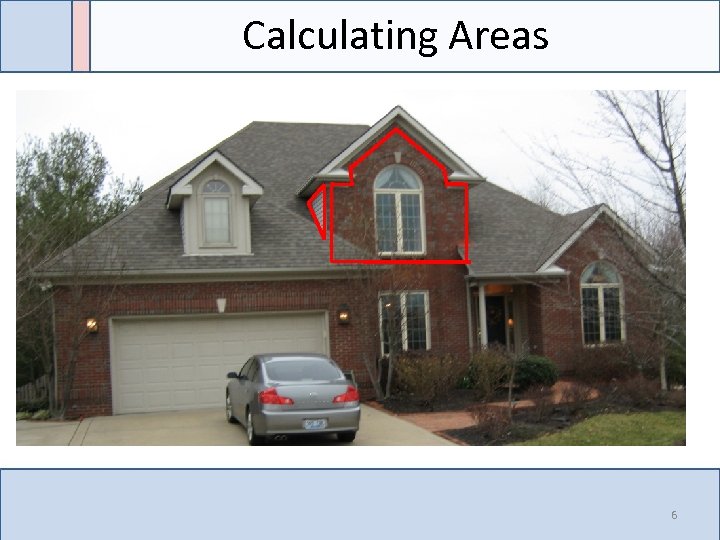
Calculating Areas 5
 Calculating Areas 6
Calculating Areas 6
 Calculating Areas 7
Calculating Areas 7
 Other Complex Shapes Insulated Hip Roof 8
Other Complex Shapes Insulated Hip Roof 8
 Develop a Sequence for Problem Solving 1. Convert Measurements to Decimals: 1 foot 3” = 1. 25 feet - - 0. 5 = 6” etc. 2. Simplify Shapes to: v Rectangles or Squares v Right Triangles (one angle is 90 degrees) v Any Shape where the Formula is Known 3. Carefully Evaluate the Known Information 4. Solve the Problem (Answer the Question) 5. Convert your answer to feet & inches OR decimals as the test question requires. 9
Develop a Sequence for Problem Solving 1. Convert Measurements to Decimals: 1 foot 3” = 1. 25 feet - - 0. 5 = 6” etc. 2. Simplify Shapes to: v Rectangles or Squares v Right Triangles (one angle is 90 degrees) v Any Shape where the Formula is Known 3. Carefully Evaluate the Known Information 4. Solve the Problem (Answer the Question) 5. Convert your answer to feet & inches OR decimals as the test question requires. 9
 Convert Measurements to Decimals Make Calculations in Decimals Convert Inches to Feet by: inches / 12 = decimal feet Remember: Convert your answer to feet & inches OR decimals as the test question requires. 10
Convert Measurements to Decimals Make Calculations in Decimals Convert Inches to Feet by: inches / 12 = decimal feet Remember: Convert your answer to feet & inches OR decimals as the test question requires. 10
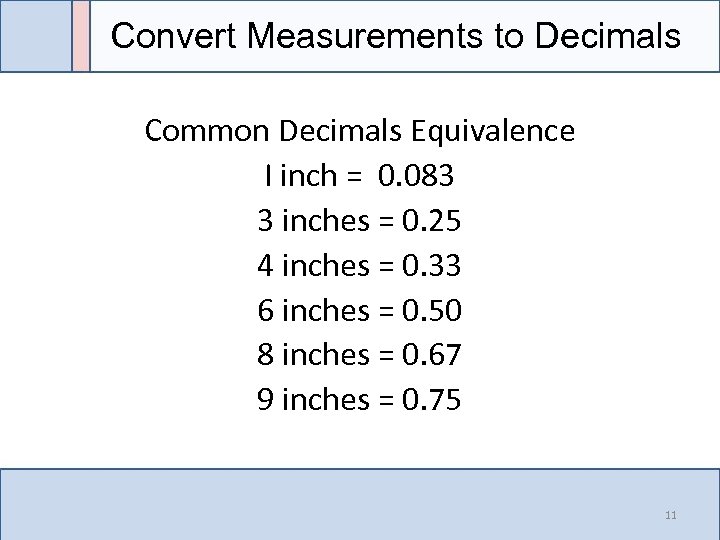 Convert Measurements to Decimals Common Decimals Equivalence I inch = 0. 083 3 inches = 0. 25 4 inches = 0. 33 6 inches = 0. 50 8 inches = 0. 67 9 inches = 0. 75 11
Convert Measurements to Decimals Common Decimals Equivalence I inch = 0. 083 3 inches = 0. 25 4 inches = 0. 33 6 inches = 0. 50 8 inches = 0. 67 9 inches = 0. 75 11
 Convert Measurements to Decimal Feet Example 4 ft 8 inches = 1/12 = 0. 67 Answer 4. 67 feet 12
Convert Measurements to Decimal Feet Example 4 ft 8 inches = 1/12 = 0. 67 Answer 4. 67 feet 12
 Convert Measurements to Feet/Inches Example 6. 25 feet 0. 25 * 12 = 3 inches Answer 6 ft 3 inches 13
Convert Measurements to Feet/Inches Example 6. 25 feet 0. 25 * 12 = 3 inches Answer 6 ft 3 inches 13
 Your Turn- Conversions Convert to Decimal Feet: Convert to Feet/Inches One foot- two inches = 3. 33 = Seven inches = 1. 92 = One foot – five inches = 4. 67 = Two feet – nine inches = 6. 08 = Three feet – ten inches = 5. 50 = 14
Your Turn- Conversions Convert to Decimal Feet: Convert to Feet/Inches One foot- two inches = 3. 33 = Seven inches = 1. 92 = One foot – five inches = 4. 67 = Two feet – nine inches = 6. 08 = Three feet – ten inches = 5. 50 = 14
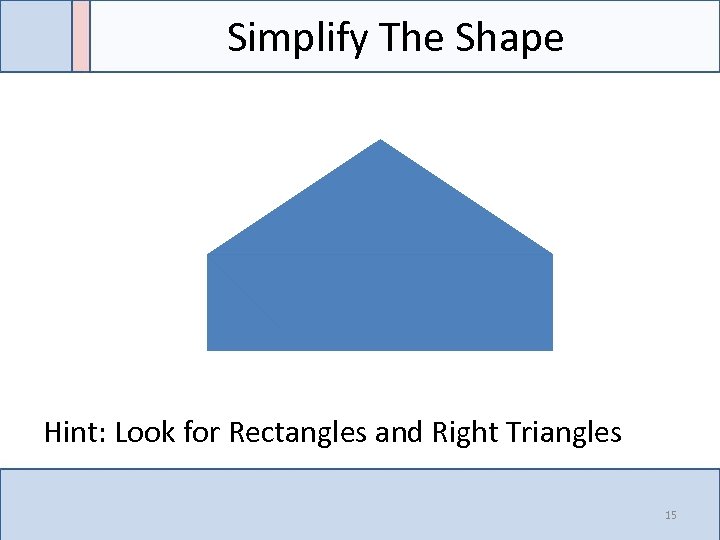 Simplify The Shape Hint: Look for Rectangles and Right Triangles 15
Simplify The Shape Hint: Look for Rectangles and Right Triangles 15
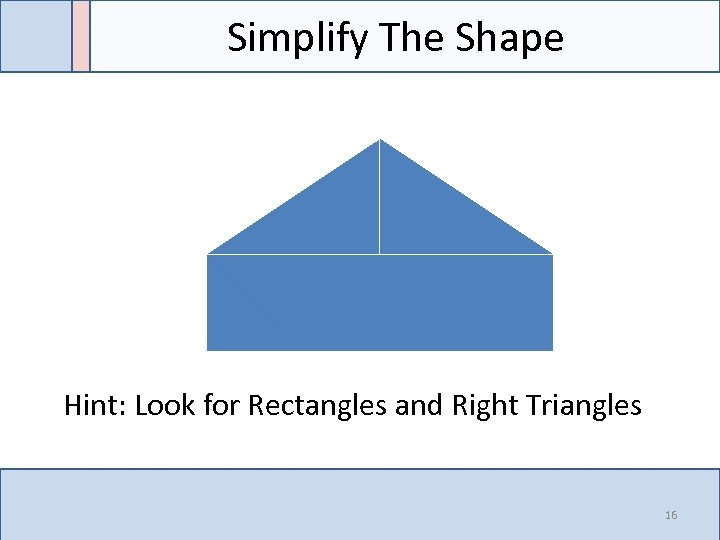 Simplify The Shape Hint: Look for Rectangles and Right Triangles 16
Simplify The Shape Hint: Look for Rectangles and Right Triangles 16
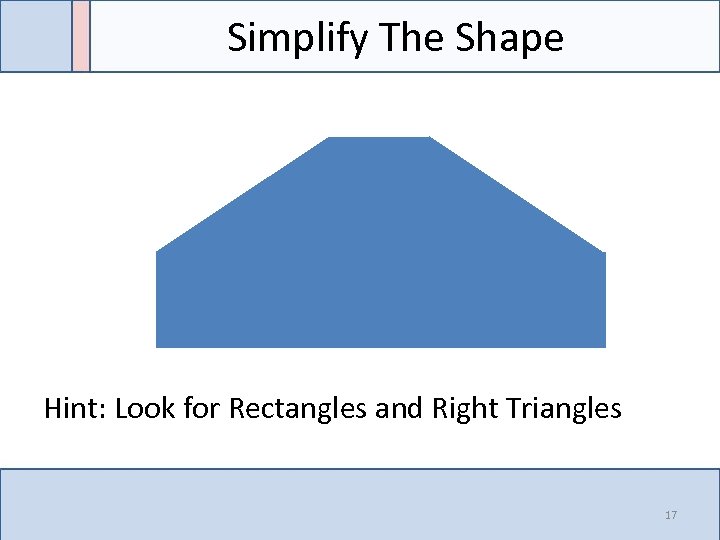 Simplify The Shape Hint: Look for Rectangles and Right Triangles 17
Simplify The Shape Hint: Look for Rectangles and Right Triangles 17
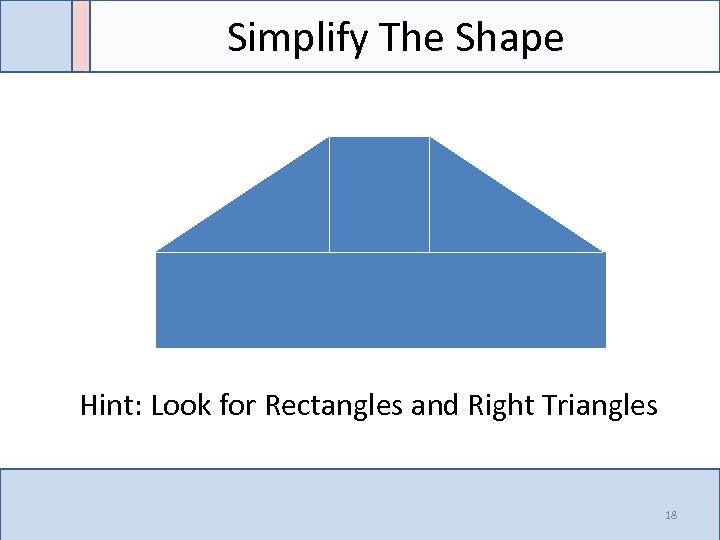 Simplify The Shape Hint: Look for Rectangles and Right Triangles 18
Simplify The Shape Hint: Look for Rectangles and Right Triangles 18
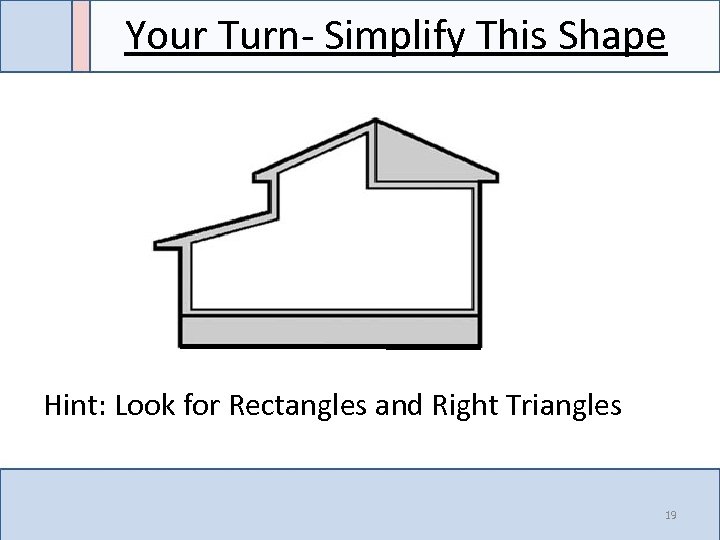 Your Turn- Simplify This Shape Hint: Look for Rectangles and Right Triangles 19
Your Turn- Simplify This Shape Hint: Look for Rectangles and Right Triangles 19
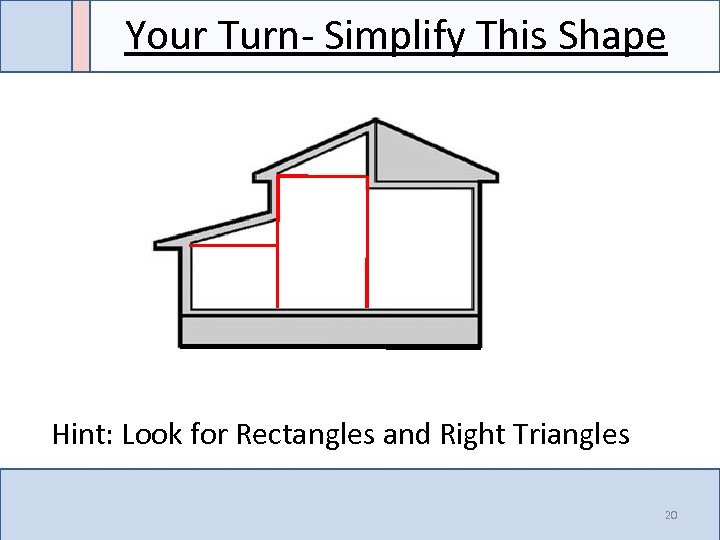 Your Turn- Simplify This Shape Hint: Look for Rectangles and Right Triangles 20
Your Turn- Simplify This Shape Hint: Look for Rectangles and Right Triangles 20
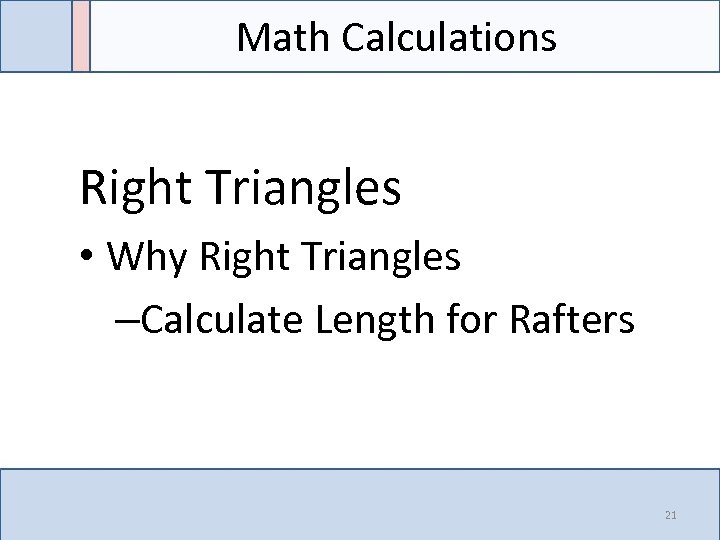 Math Calculations Right Triangles • Why Right Triangles –Calculate Length for Rafters 21
Math Calculations Right Triangles • Why Right Triangles –Calculate Length for Rafters 21
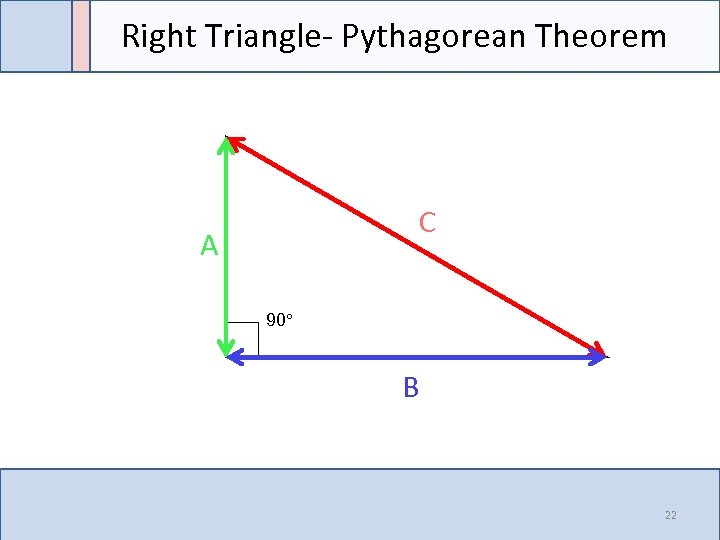 Right Triangle- Pythagorean Theorem C A 90° B 22
Right Triangle- Pythagorean Theorem C A 90° B 22
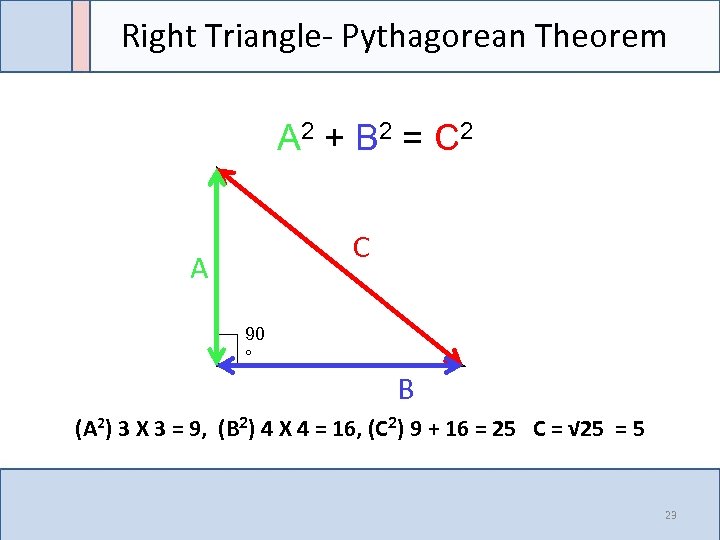 Right Triangle- Pythagorean Theorem A 2 + B 2 = C 2 C A 90 ° B (A 2) 3 X 3 = 9, (B 2) 4 X 4 = 16, (C 2) 9 + 16 = 25 C = √ 25 = 5 23
Right Triangle- Pythagorean Theorem A 2 + B 2 = C 2 C A 90 ° B (A 2) 3 X 3 = 9, (B 2) 4 X 4 = 16, (C 2) 9 + 16 = 25 C = √ 25 = 5 23
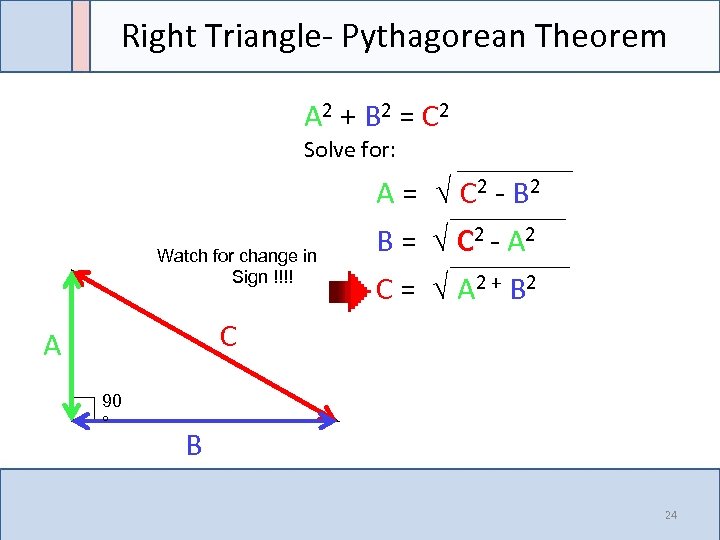 Right Triangle- Pythagorean Theorem A 2 + B 2 = C 2 Solve for: _______________ A = √ C 2 - B 2 B = √ C 2 - A 2 C = √ A 2 + B 2 _______________ Watch for change in Sign !!!! _______________ C A 90 ° B 24
Right Triangle- Pythagorean Theorem A 2 + B 2 = C 2 Solve for: _______________ A = √ C 2 - B 2 B = √ C 2 - A 2 C = √ A 2 + B 2 _______________ Watch for change in Sign !!!! _______________ C A 90 ° B 24
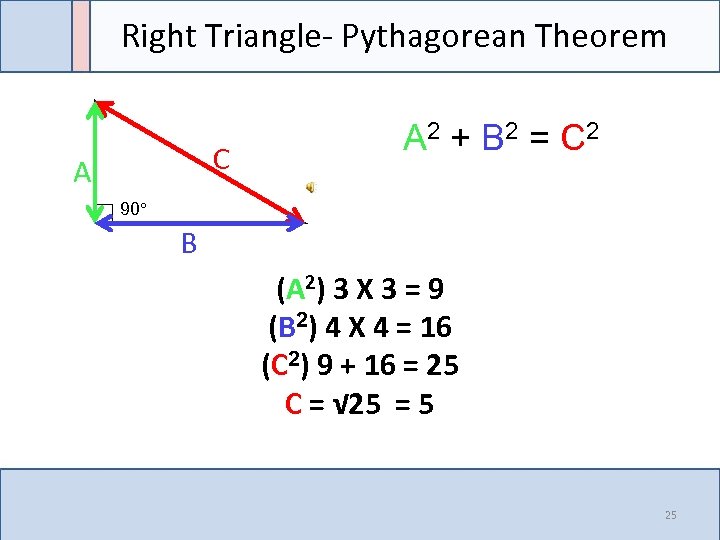 Right Triangle- Pythagorean Theorem C A A 2 + B 2 = C 2 90° B (A 2) 3 X 3 = 9 (B 2) 4 X 4 = 16 (C 2) 9 + 16 = 25 C = √ 25 = 5 25
Right Triangle- Pythagorean Theorem C A A 2 + B 2 = C 2 90° B (A 2) 3 X 3 = 9 (B 2) 4 X 4 = 16 (C 2) 9 + 16 = 25 C = √ 25 = 5 25
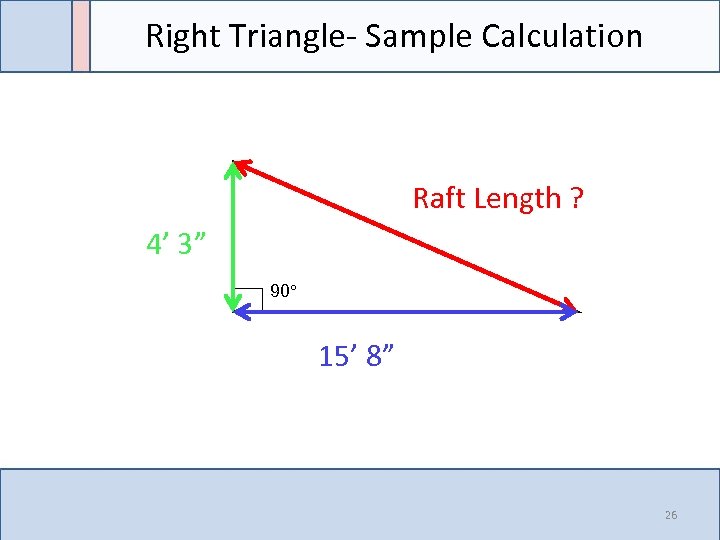 Right Triangle- Sample Calculation Raft Length ? 4’ 3” 90° 15’ 8” 26
Right Triangle- Sample Calculation Raft Length ? 4’ 3” 90° 15’ 8” 26
 Right Triangle- Sample Calculation Raft Length ? 4’ 3” 90° 15’ 8” 3 inches = 3/12 ft = 0. 25 ft 4’ 3” = 4. 25 ft 8 inches = 8/12 ft = 0. 67 ft 15’ 8’ = 15. 67 ft 27
Right Triangle- Sample Calculation Raft Length ? 4’ 3” 90° 15’ 8” 3 inches = 3/12 ft = 0. 25 ft 4’ 3” = 4. 25 ft 8 inches = 8/12 ft = 0. 67 ft 15’ 8’ = 15. 67 ft 27
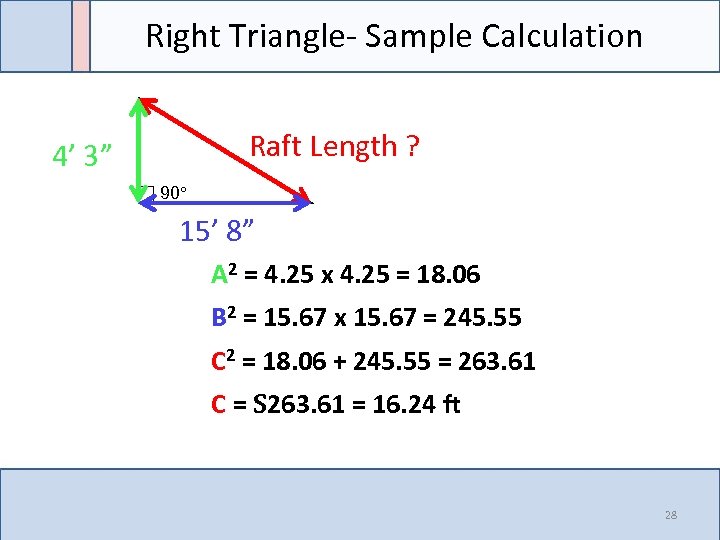 Right Triangle- Sample Calculation Raft Length ? 4’ 3” 90° 15’ 8” A 2 = 4. 25 x 4. 25 = 18. 06 B 2 = 15. 67 x 15. 67 = 245. 55 C 2 = 18. 06 + 245. 55 = 263. 61 C = S 263. 61 = 16. 24 ft 28
Right Triangle- Sample Calculation Raft Length ? 4’ 3” 90° 15’ 8” A 2 = 4. 25 x 4. 25 = 18. 06 B 2 = 15. 67 x 15. 67 = 245. 55 C 2 = 18. 06 + 245. 55 = 263. 61 C = S 263. 61 = 16. 24 ft 28
 Math Calculations Ratios • Why Ratios –Using Roof Pitch in Calculations 29
Math Calculations Ratios • Why Ratios –Using Roof Pitch in Calculations 29
 Everyday Use of Ratio’s • Your going to buy lawn fertilizer – Your lawn is 10, 000 ft 2 – The fertilizer bag label is: – 1 bag per 2000 ft 2 • How many bags do you buy? 30
Everyday Use of Ratio’s • Your going to buy lawn fertilizer – Your lawn is 10, 000 ft 2 – The fertilizer bag label is: – 1 bag per 2000 ft 2 • How many bags do you buy? 30
 Everyday Use of Ratio’s • How many bags do you buy? If 1 bag covers 2, 000 then 10, 000/2, 000 = 5 bags As a Ratio 1 bag = “X” bags 2, 000 ft² 10, 000 ft² Cross multiply 10, 000 ft² x 1 bag = “X” bags x 2, 000 ft² “X” bags = 1 bag * 10, 000 ft² 2, 000 ft² X bags = 5 Divide 31
Everyday Use of Ratio’s • How many bags do you buy? If 1 bag covers 2, 000 then 10, 000/2, 000 = 5 bags As a Ratio 1 bag = “X” bags 2, 000 ft² 10, 000 ft² Cross multiply 10, 000 ft² x 1 bag = “X” bags x 2, 000 ft² “X” bags = 1 bag * 10, 000 ft² 2, 000 ft² X bags = 5 Divide 31
 Everyday Use of Ratio’s • Your going to make chili for 2 people – Recipe is of 4 people – The recipe calls for 3 teaspoons of hot pepper • How much hot pepper do you put in? – The right amount not fire engine chili 32
Everyday Use of Ratio’s • Your going to make chili for 2 people – Recipe is of 4 people – The recipe calls for 3 teaspoons of hot pepper • How much hot pepper do you put in? – The right amount not fire engine chili 32
 Everyday Use of Ratio’s • How much hot pepper do you put in? If 3 teaspoons is for 4 people then 1 ½ teaspoons is for 2 people As a Ratio 3 teaspoons = “X” teaspoons 4 people 2 people x 3 teaspoons = “X” teaspoons x 4 people X teaspoons = 3 teaspoons x 2 people 4 people X = 1. 5 teaspoons or 1 ½ teaspoons 33
Everyday Use of Ratio’s • How much hot pepper do you put in? If 3 teaspoons is for 4 people then 1 ½ teaspoons is for 2 people As a Ratio 3 teaspoons = “X” teaspoons 4 people 2 people x 3 teaspoons = “X” teaspoons x 4 people X teaspoons = 3 teaspoons x 2 people 4 people X = 1. 5 teaspoons or 1 ½ teaspoons 33
 Units of Ratio’s They have to be the same on both sides of the = 1 bag = X bags 2, 000 ft² 10, 000 ft² 3 teaspoons 4 people = X teaspoons 2 people 34
Units of Ratio’s They have to be the same on both sides of the = 1 bag = X bags 2, 000 ft² 10, 000 ft² 3 teaspoons 4 people = X teaspoons 2 people 34
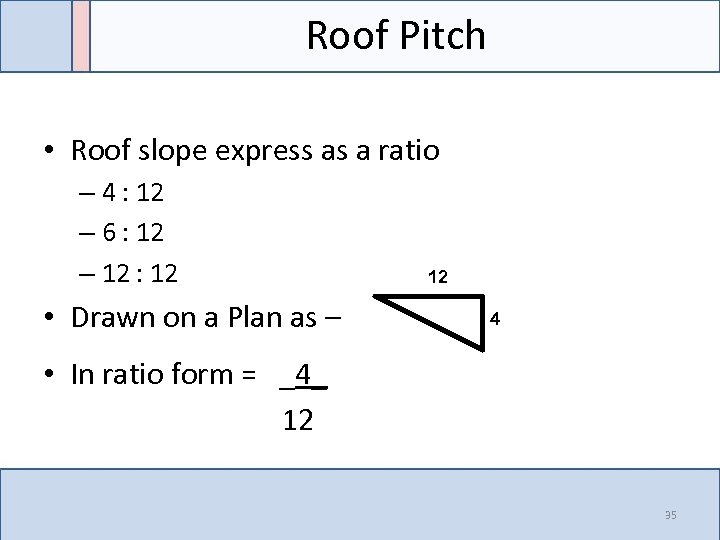 Roof Pitch • Roof slope express as a ratio – 4 : 12 – 6 : 12 – 12 : 12 • Drawn on a Plan as – 12 4 • In ratio form = _4_ 12 35
Roof Pitch • Roof slope express as a ratio – 4 : 12 – 6 : 12 – 12 : 12 • Drawn on a Plan as – 12 4 • In ratio form = _4_ 12 35
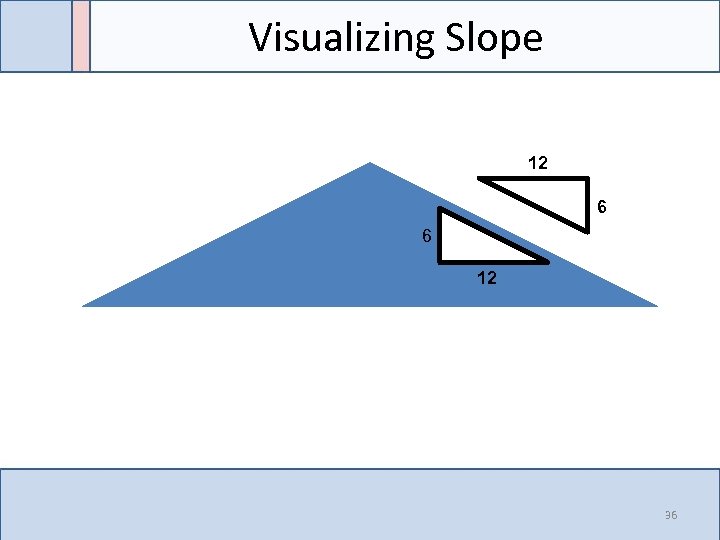 Visualizing Slope 12 Z 6 6 12 36
Visualizing Slope 12 Z 6 6 12 36
 Calculating Rise or Run Slope = 4 : 12 or Rise : Run 4 12 Z Rise Run X On Blueprints, Slope = “X” : 12 12 ”x” = Rise 12 Run 37
Calculating Rise or Run Slope = 4 : 12 or Rise : Run 4 12 Z Rise Run X On Blueprints, Slope = “X” : 12 12 ”x” = Rise 12 Run 37
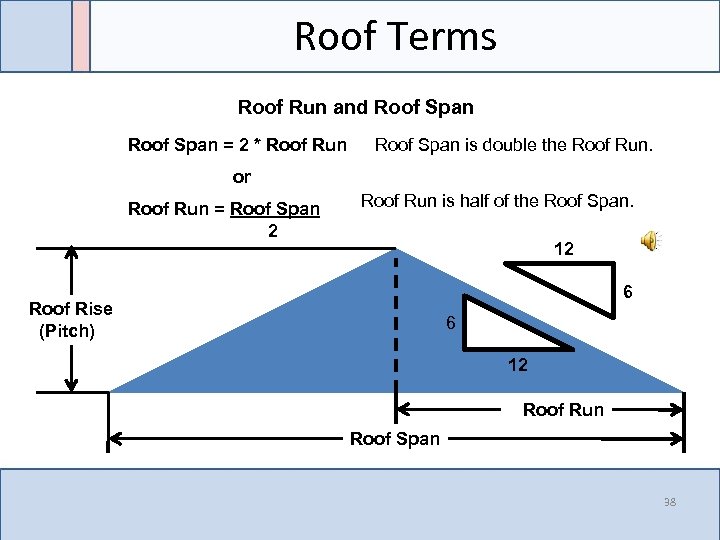 Roof Terms Roof Run and Roof Span = 2 * Roof Run Roof Span is double the Roof Run. or Roof Run is half of the Roof Span. Roof Run = Roof Span 2 12 Z Roof Rise (Pitch) 6 6 12 Roof Run Roof Span 38
Roof Terms Roof Run and Roof Span = 2 * Roof Run Roof Span is double the Roof Run. or Roof Run is half of the Roof Span. Roof Run = Roof Span 2 12 Z Roof Rise (Pitch) 6 6 12 Roof Run Roof Span 38
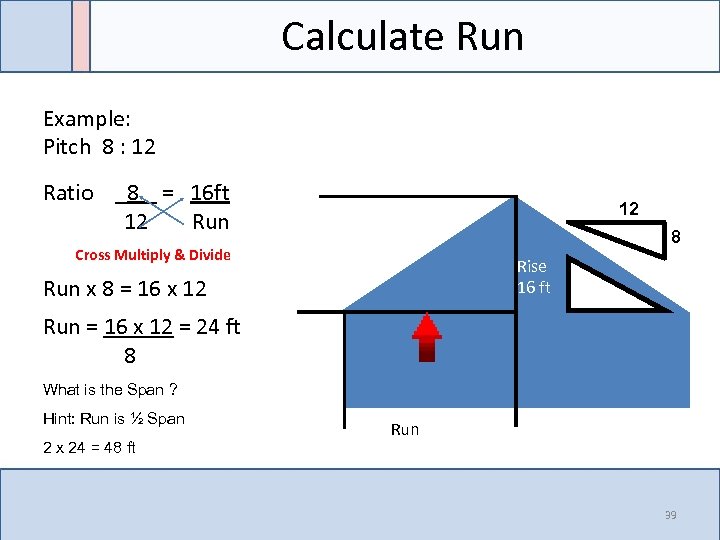 Calculate Run Example: Pitch 8 : 12 Ratio _8 _ = 16 ft 12 Run 12 8 Cross Multiply & Divide Rise Z 16 ft 8 Run x 8 = 16 x 12 8 Run = 16 x 12 = 24 ft 8 What is the Span ? Hint: Run is ½ Span 2 x 24 = 48 ft Run 39
Calculate Run Example: Pitch 8 : 12 Ratio _8 _ = 16 ft 12 Run 12 8 Cross Multiply & Divide Rise Z 16 ft 8 Run x 8 = 16 x 12 8 Run = 16 x 12 = 24 ft 8 What is the Span ? Hint: Run is ½ Span 2 x 24 = 48 ft Run 39
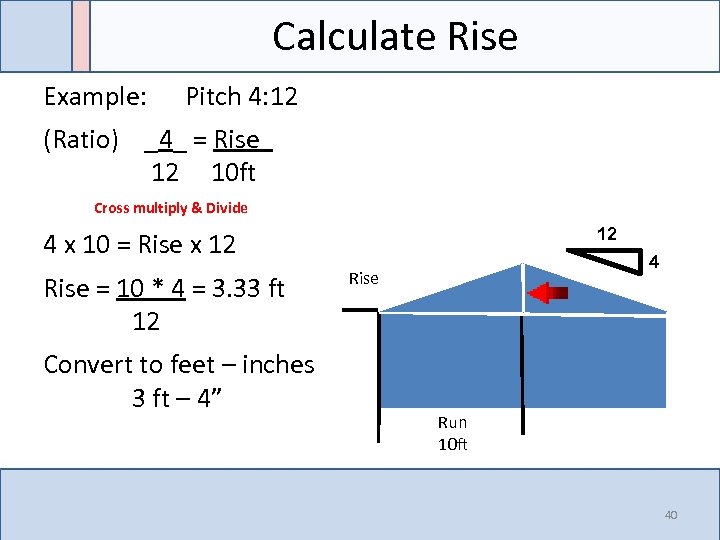 Calculate Rise Example: Pitch 4: 12 (Ratio) _4_ = Rise 12 10 ft Cross multiply & Divide 12 4 x 10 = Rise x 12 Rise = 10 * 4 = 3. 33 ft 12 Convert to feet – inches 3 ft – 4” 4 Rise Run 10 ft 40
Calculate Rise Example: Pitch 4: 12 (Ratio) _4_ = Rise 12 10 ft Cross multiply & Divide 12 4 x 10 = Rise x 12 Rise = 10 * 4 = 3. 33 ft 12 Convert to feet – inches 3 ft – 4” 4 Rise Run 10 ft 40
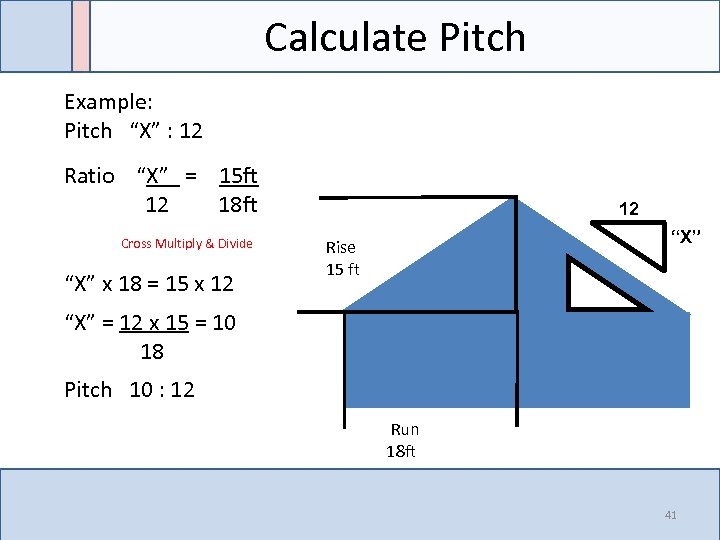 Calculate Pitch Example: Pitch “X” : 12 Ratio “X” = 15 ft 12 18 ft Cross Multiply & Divide “X” x 18 = 15 x 12 12 “X” Rise 15 ft Z “X” = 12 x 15 = 10 18 Pitch 10 : 12 Run 18 ft 41
Calculate Pitch Example: Pitch “X” : 12 Ratio “X” = 15 ft 12 18 ft Cross Multiply & Divide “X” x 18 = 15 x 12 12 “X” Rise 15 ft Z “X” = 12 x 15 = 10 18 Pitch 10 : 12 Run 18 ft 41
 Roof Pitch Calculations Your Turn 42
Roof Pitch Calculations Your Turn 42
 Calculating Perimeter, Area and Volume Two Most Common Shapes: • Rectangles • Triangles 43
Calculating Perimeter, Area and Volume Two Most Common Shapes: • Rectangles • Triangles 43
 Calculating Perimeter - Rectangle Perimeter = Distance around the outside edge P = 2 x length + 2 x width length width 44
Calculating Perimeter - Rectangle Perimeter = Distance around the outside edge P = 2 x length + 2 x width length width 44
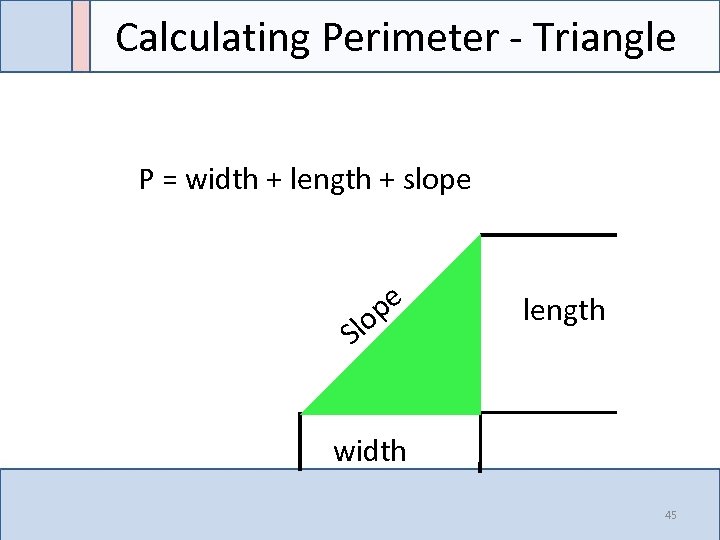 Calculating Perimeter - Triangle P = width + length + slope pe o Sl length width 45
Calculating Perimeter - Triangle P = width + length + slope pe o Sl length width 45
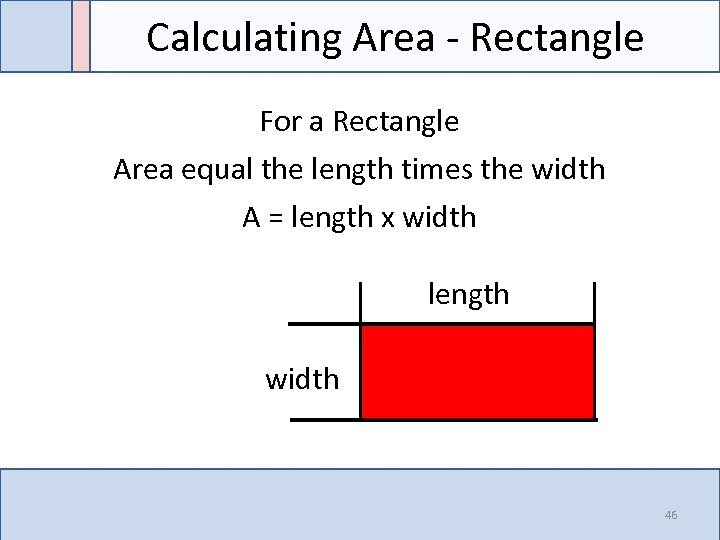 Calculating Area - Rectangle For a Rectangle Area equal the length times the width A = length x width length width 46
Calculating Area - Rectangle For a Rectangle Area equal the length times the width A = length x width length width 46
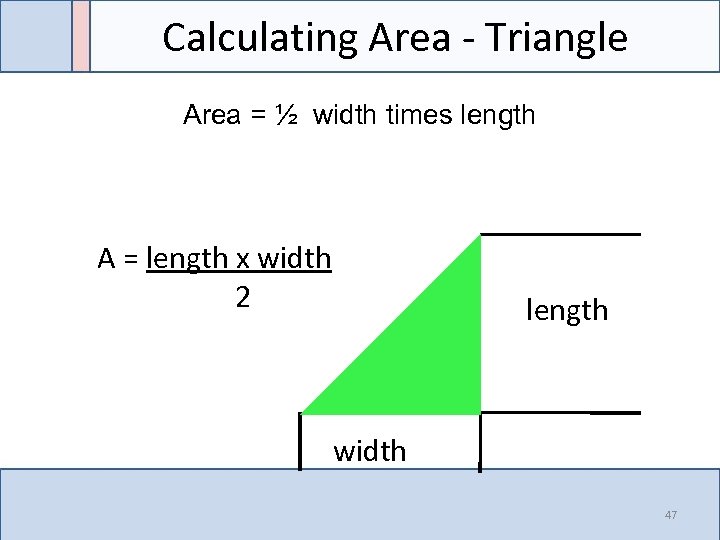 Calculating Area - Triangle Area = ½ width times length A = length x width 2 length width 47
Calculating Area - Triangle Area = ½ width times length A = length x width 2 length width 47
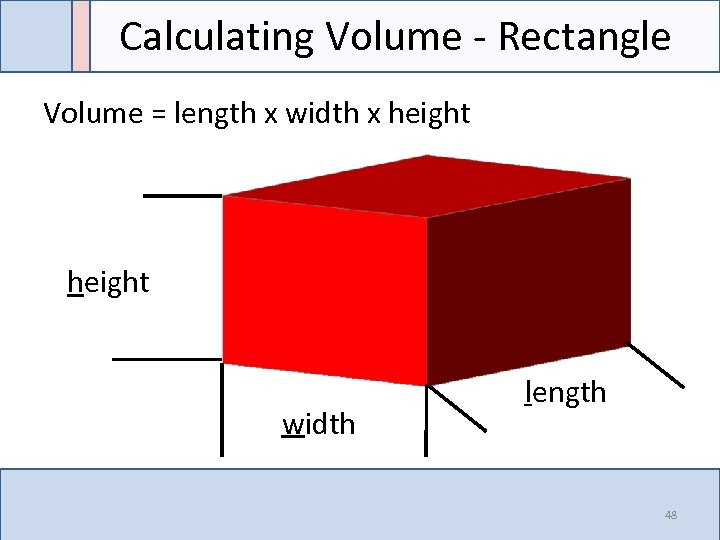 Calculating Volume - Rectangle Volume = length x width x height width length 48
Calculating Volume - Rectangle Volume = length x width x height width length 48
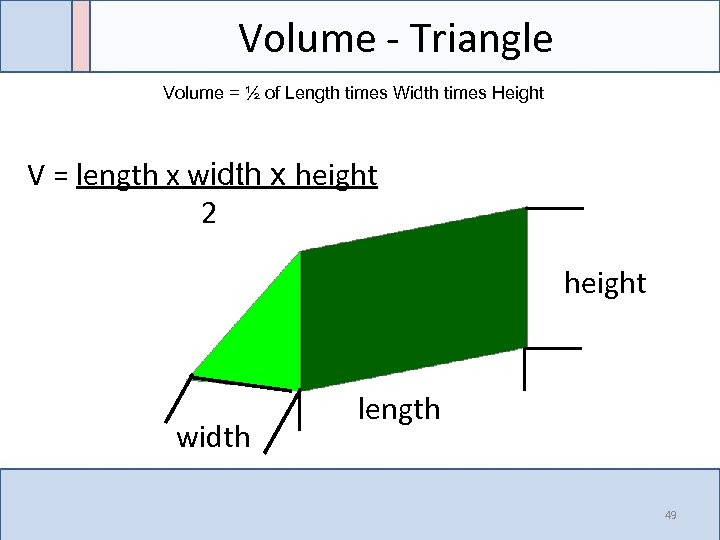 Volume - Triangle Volume = ½ of Length times Width times Height V = length x width x height 2 height width length 49
Volume - Triangle Volume = ½ of Length times Width times Height V = length x width x height 2 height width length 49
 Applying the Calculations • Floor Area • Wall Area • Conditioned Space Volume 50
Applying the Calculations • Floor Area • Wall Area • Conditioned Space Volume 50
 Area by Component 2) (ft 51
Area by Component 2) (ft 51
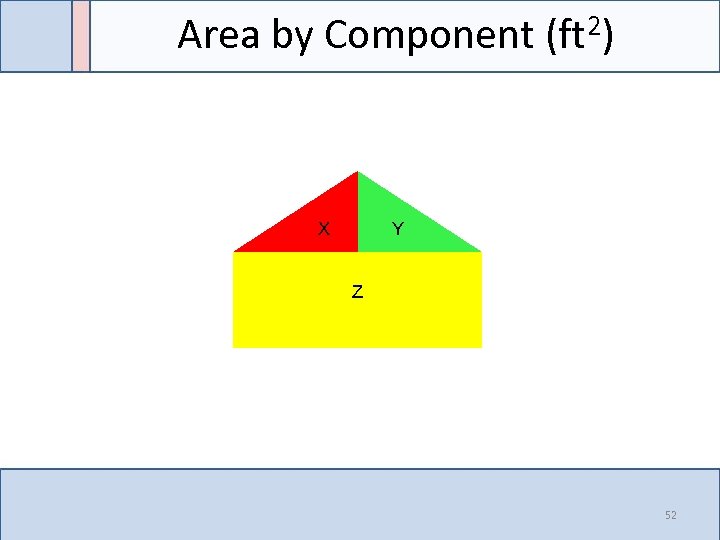 Area by Component (ft 2) X Y Z 52
Area by Component (ft 2) X Y Z 52
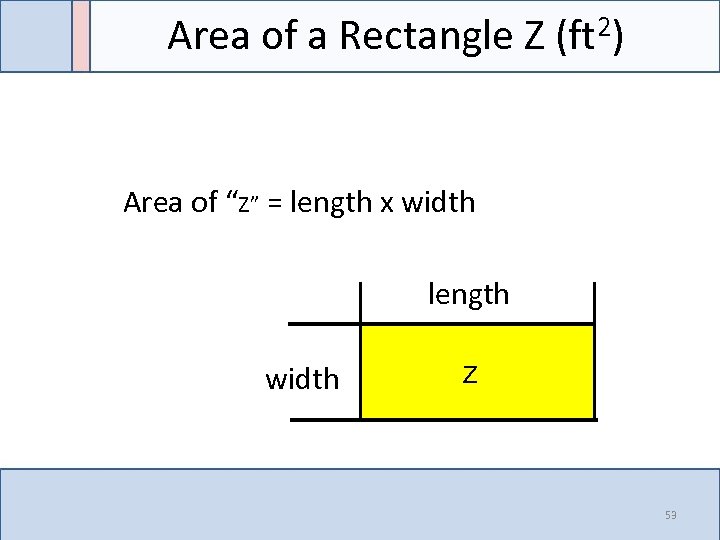 Area of a Rectangle Z (ft 2) Area of “Z” = length x width length width Z 53
Area of a Rectangle Z (ft 2) Area of “Z” = length x width length width Z 53
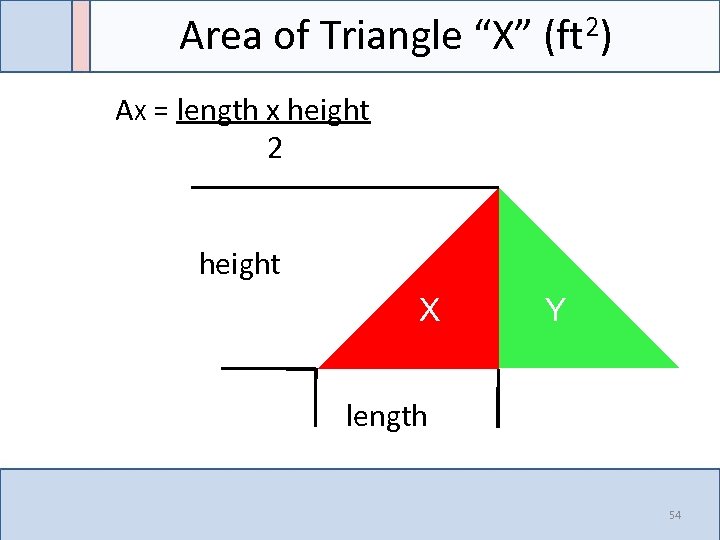 Area of Triangle “X” (ft 2) AX = length x height 2 height X Y length 54
Area of Triangle “X” (ft 2) AX = length x height 2 height X Y length 54
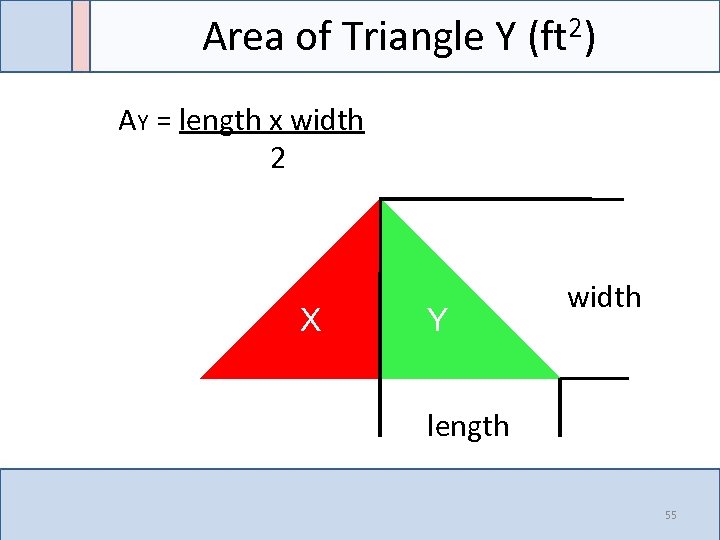 Area of Triangle Y (ft 2) AY = length x width 2 X Y width length 55
Area of Triangle Y (ft 2) AY = length x width 2 X Y width length 55
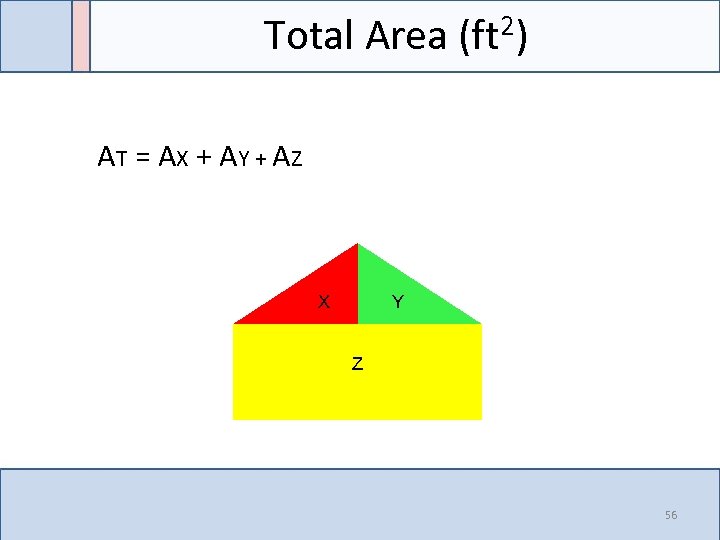 Total Area 2) (ft AT = A X + A Y + AZ X Y Z 56
Total Area 2) (ft AT = A X + A Y + AZ X Y Z 56
 Area by Component (ft 2) 57
Area by Component (ft 2) 57
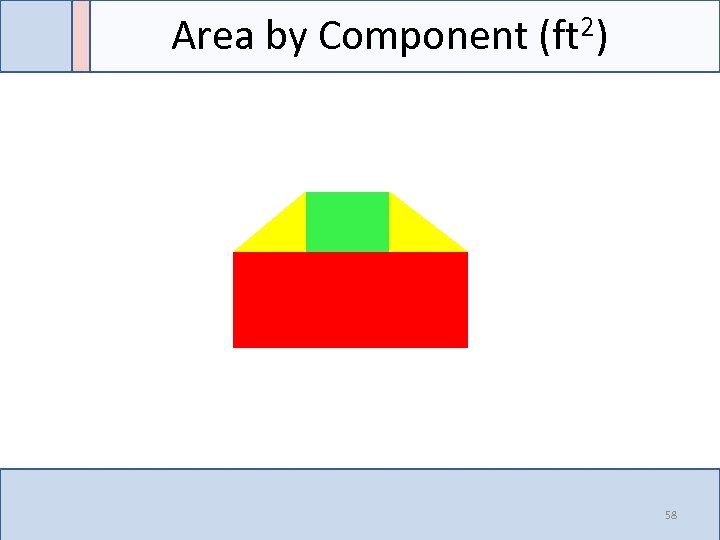 Area by Component (ft 2) 58
Area by Component (ft 2) 58
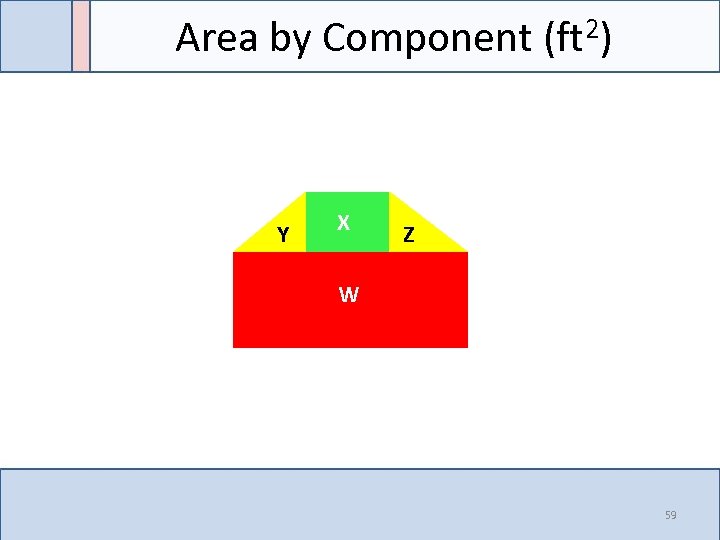 Area by Component (ft 2) Y X Z W 59
Area by Component (ft 2) Y X Z W 59
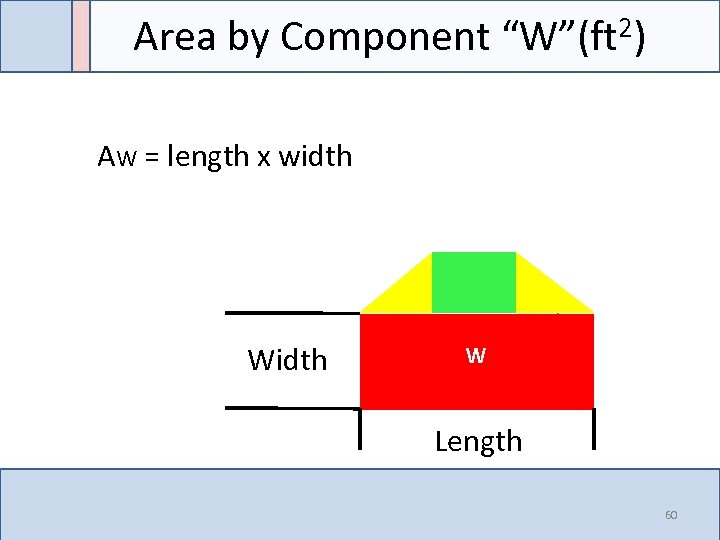 Area by Component “W”(ft 2) AW = length x width W Length 60
Area by Component “W”(ft 2) AW = length x width W Length 60
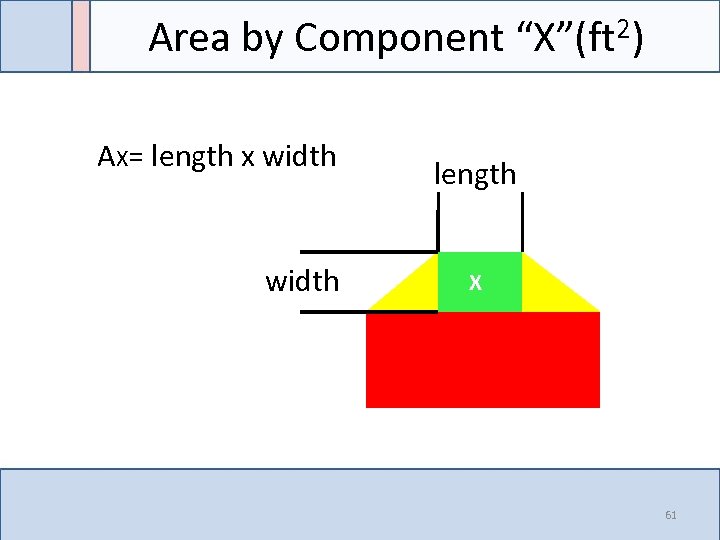 Area by Component “X”(ft 2) AX= length x width length X 61
Area by Component “X”(ft 2) AX= length x width length X 61
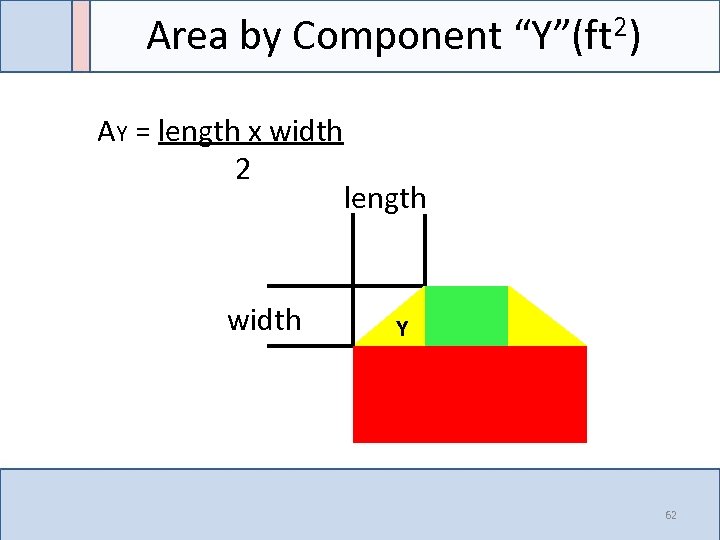 Area by Component “Y”(ft 2) AY = length x width 2 width length Y Length 62
Area by Component “Y”(ft 2) AY = length x width 2 width length Y Length 62
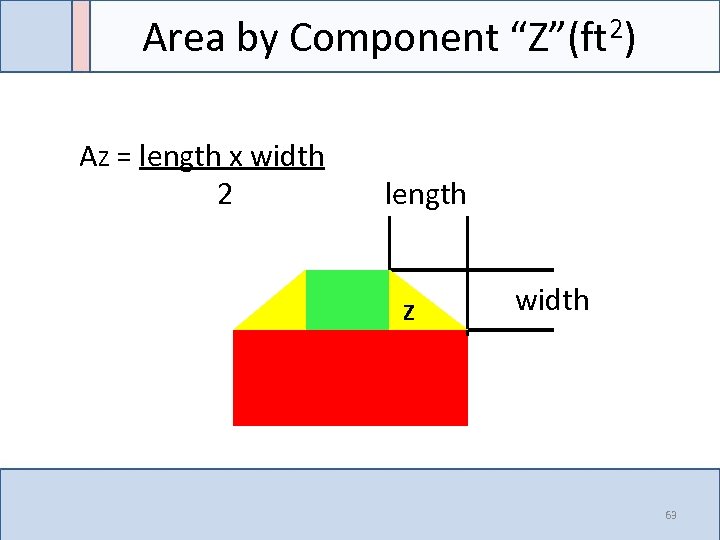 Area by Component “Z”(ft 2) AZ = length x width 2 length Z width 63
Area by Component “Z”(ft 2) AZ = length x width 2 length Z width 63
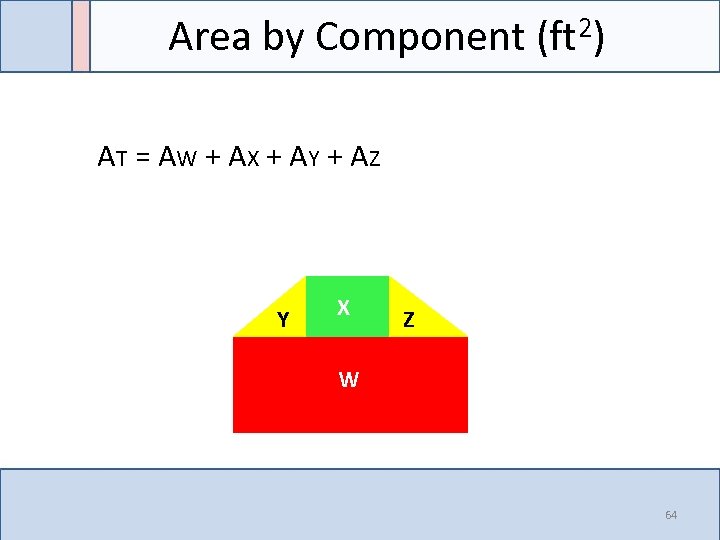 Area by Component (ft 2) AT = A W + A X + A Y + A Z Y X Z W 64
Area by Component (ft 2) AT = A W + A X + A Y + A Z Y X Z W 64
 3) (ft Calculating Volume A Room with a Cathedral Ceiling 65
3) (ft Calculating Volume A Room with a Cathedral Ceiling 65
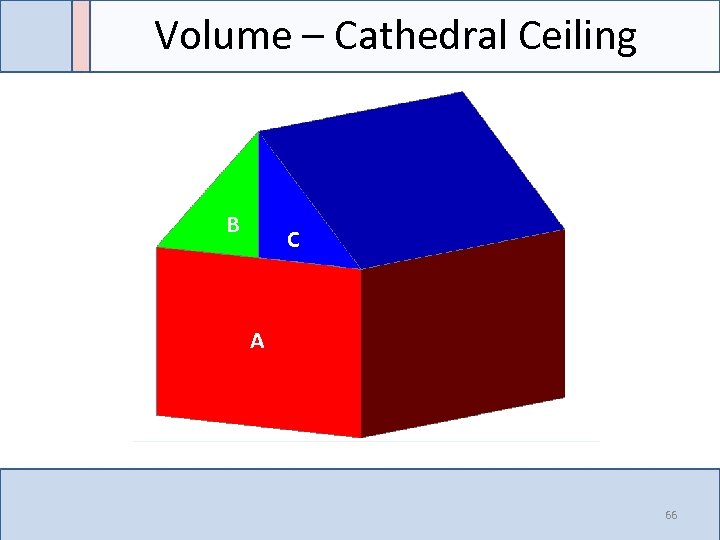 Volume – Cathedral Ceiling B C A 66
Volume – Cathedral Ceiling B C A 66
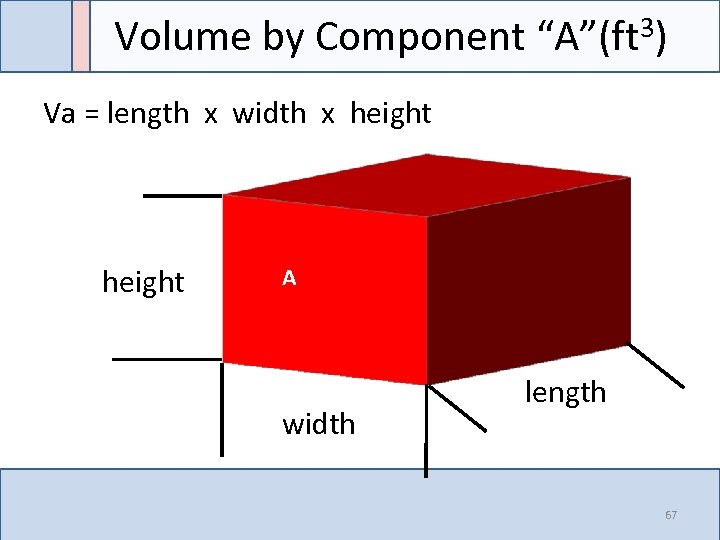 Volume by Component “A”(ft 3) Va = length x width x height A width length 67
Volume by Component “A”(ft 3) Va = length x width x height A width length 67
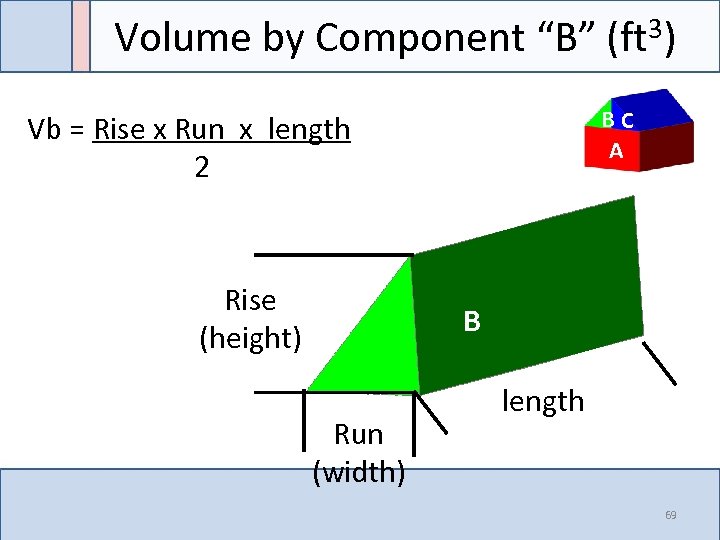 Volume by Component “B” (ft 3) BC A Vb = Rise x Run x length 2 Rise (height) B Run (width) length 69
Volume by Component “B” (ft 3) BC A Vb = Rise x Run x length 2 Rise (height) B Run (width) length 69
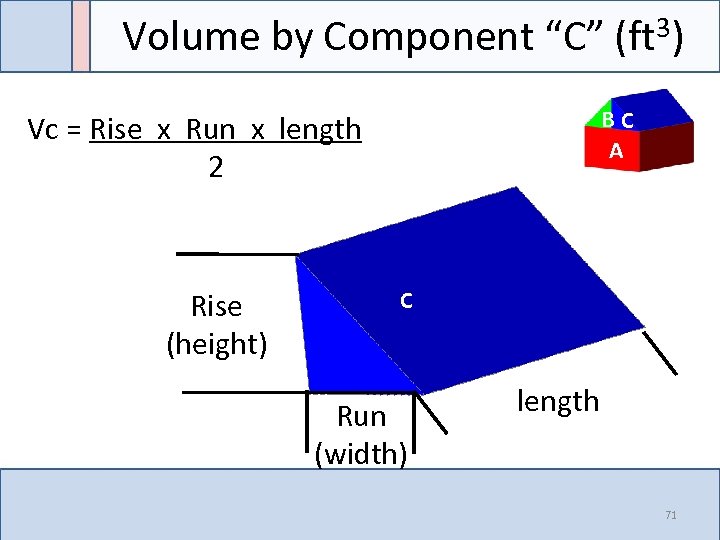 Volume by Component “C” (ft 3) BC A Vc = Rise x Run x length 2 Rise (height) C Run (width) length 71
Volume by Component “C” (ft 3) BC A Vc = Rise x Run x length 2 Rise (height) C Run (width) length 71
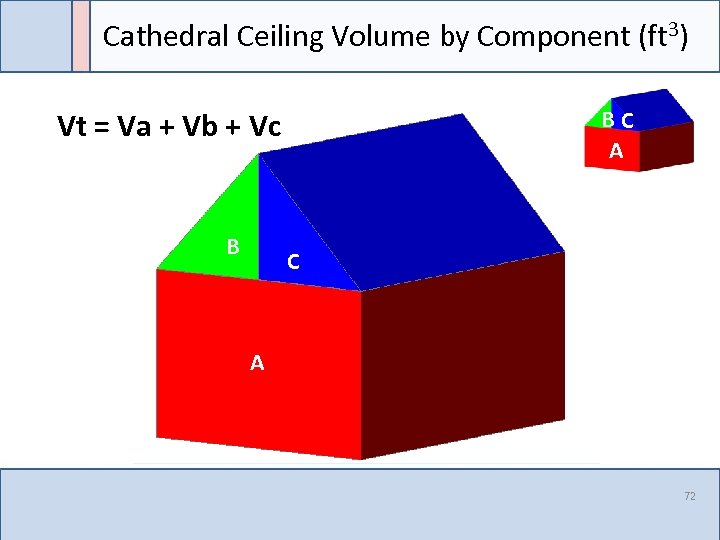 Cathedral Ceiling Volume by Component (ft 3) BC A Vt = Va + Vb + Vc B C A 72
Cathedral Ceiling Volume by Component (ft 3) BC A Vt = Va + Vb + Vc B C A 72
 Volume - Kneewall Z 73
Volume - Kneewall Z 73
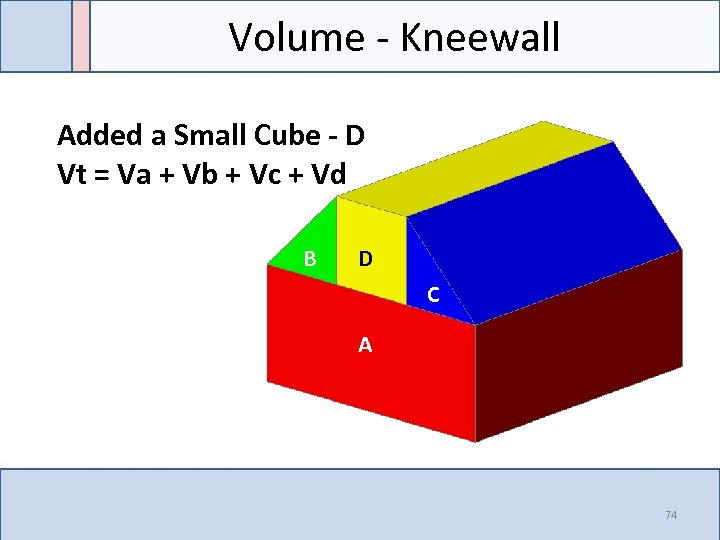 Volume - Kneewall Added a Small Cube - D Vt = Va + Vb + Vc + Vd B D B Z C A 74
Volume - Kneewall Added a Small Cube - D Vt = Va + Vb + Vc + Vd B D B Z C A 74
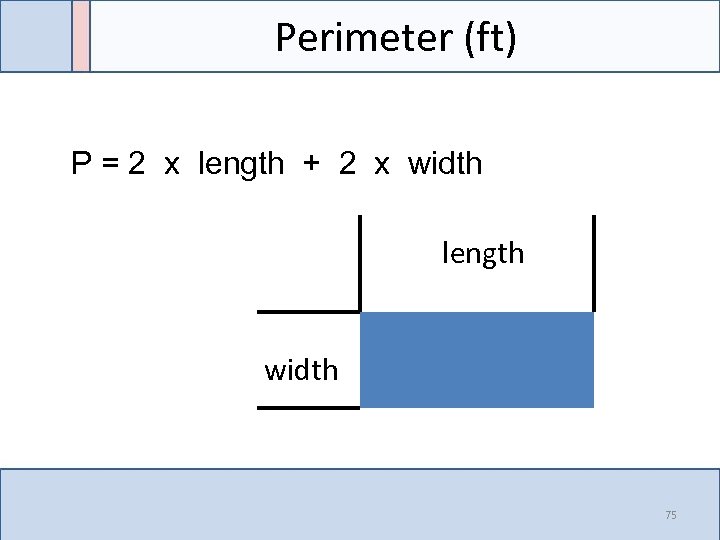 Perimeter (ft) P = 2 x length + 2 x width length width 75
Perimeter (ft) P = 2 x length + 2 x width length width 75
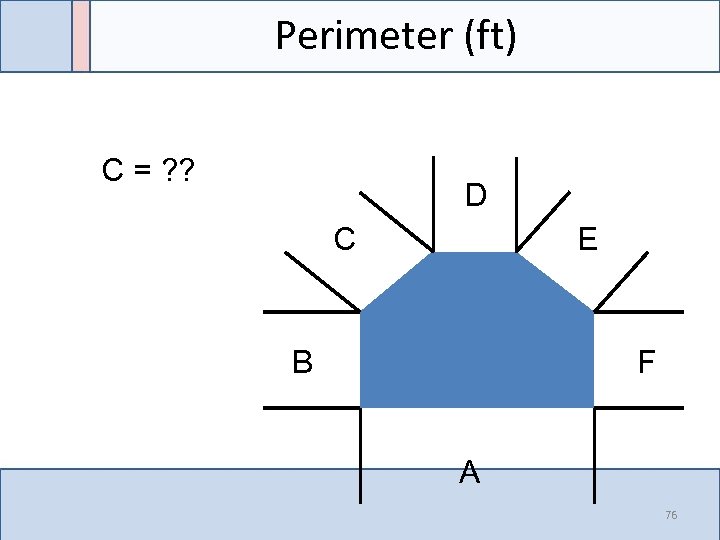 Perimeter (ft) C = ? ? D C E B F A 76
Perimeter (ft) C = ? ? D C E B F A 76
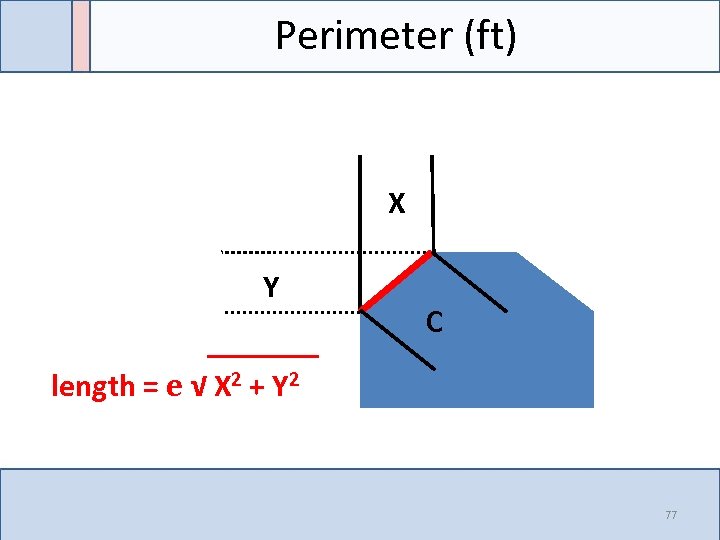 Perimeter (ft) X Y C length = e √ X 2 + Y 2 77
Perimeter (ft) X Y C length = e √ X 2 + Y 2 77
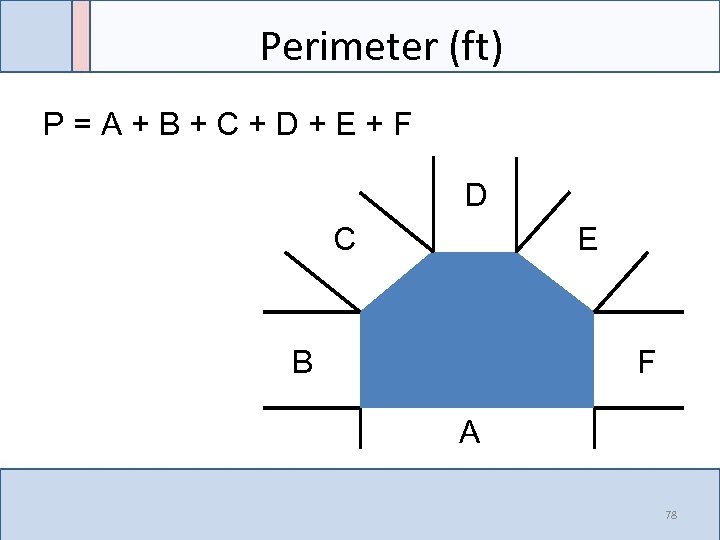 Perimeter (ft) P=A+B+C+D+E+F D C E B F A 78
Perimeter (ft) P=A+B+C+D+E+F D C E B F A 78
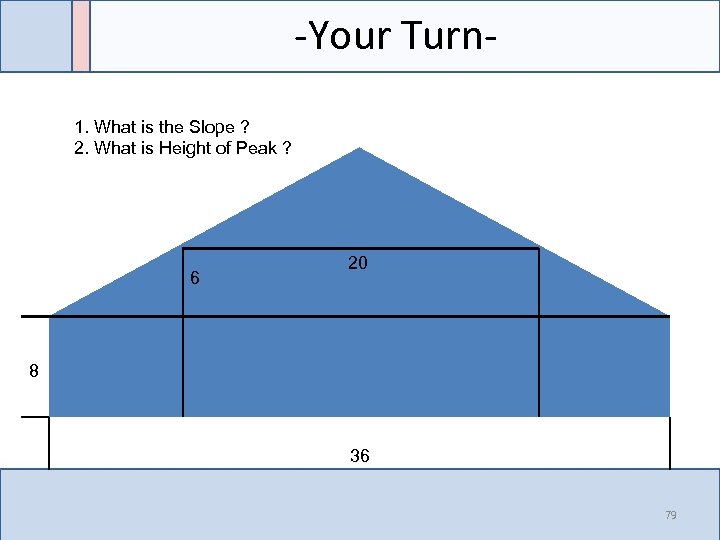 -Your Turn 1. What is the Slope ? 2. What is Height of Peak ? 6 20 8 36 79
-Your Turn 1. What is the Slope ? 2. What is Height of Peak ? 6 20 8 36 79
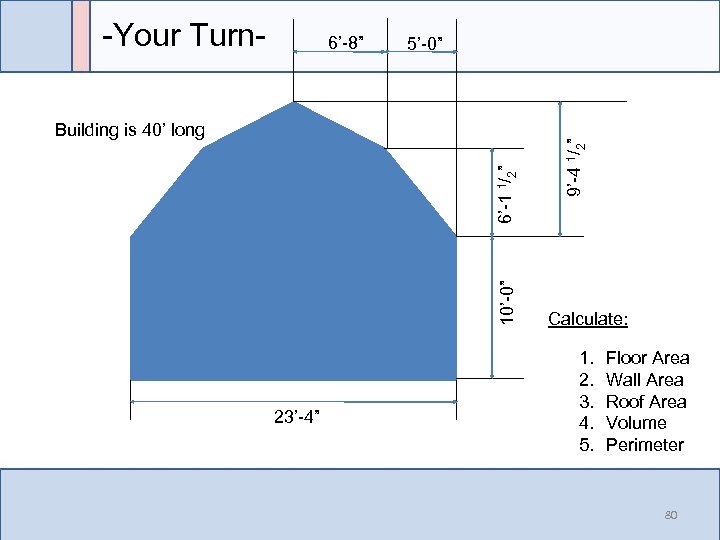 6’-8” 5’-0” 10’-0” 6’-1 1/2” Building is 40’ long 23’-4” 9’-4 1/2” -Your Turn- Calculate: 1. 2. 3. 4. 5. Floor Area Wall Area Roof Area Volume Perimeter 80
6’-8” 5’-0” 10’-0” 6’-1 1/2” Building is 40’ long 23’-4” 9’-4 1/2” -Your Turn- Calculate: 1. 2. 3. 4. 5. Floor Area Wall Area Roof Area Volume Perimeter 80
 Working with a Circular Shape 81
Working with a Circular Shape 81
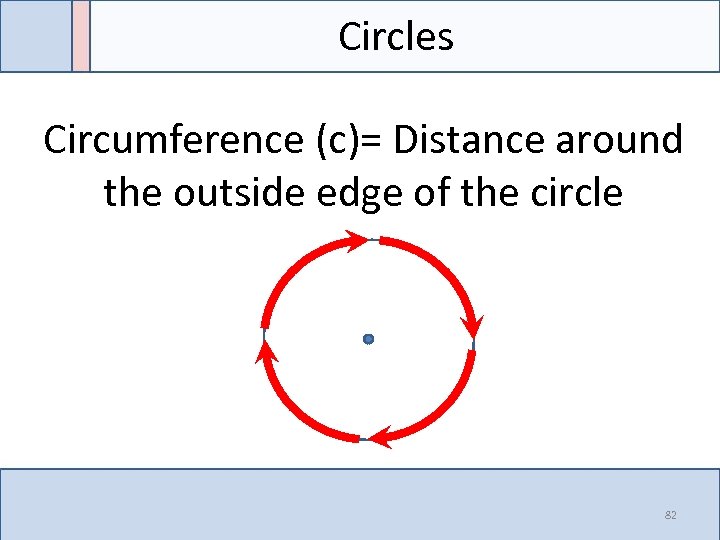 Circles Circumference (c)= Distance around the outside edge of the circle 82
Circles Circumference (c)= Distance around the outside edge of the circle 82
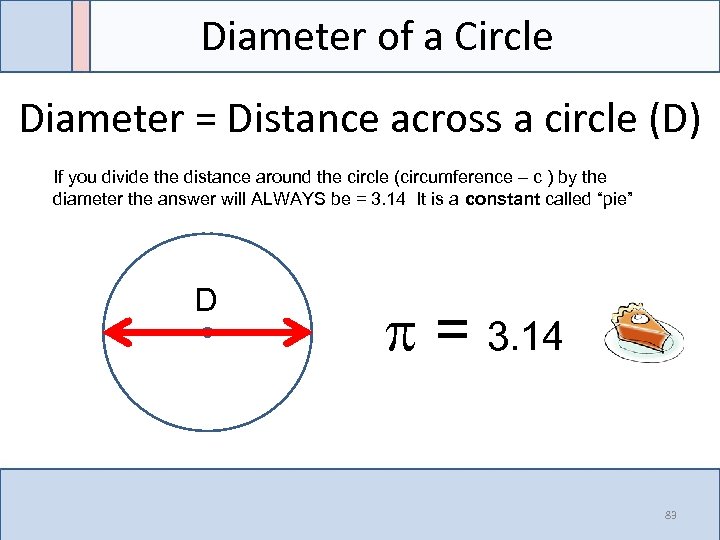 Diameter of a Circle Diameter = Distance across a circle (D) If you divide the distance around the circle (circumference – c ) by the diameter the answer will ALWAYS be = 3. 14 It is a constant called “pie” D = 3. 14 83
Diameter of a Circle Diameter = Distance across a circle (D) If you divide the distance around the circle (circumference – c ) by the diameter the answer will ALWAYS be = 3. 14 It is a constant called “pie” D = 3. 14 83
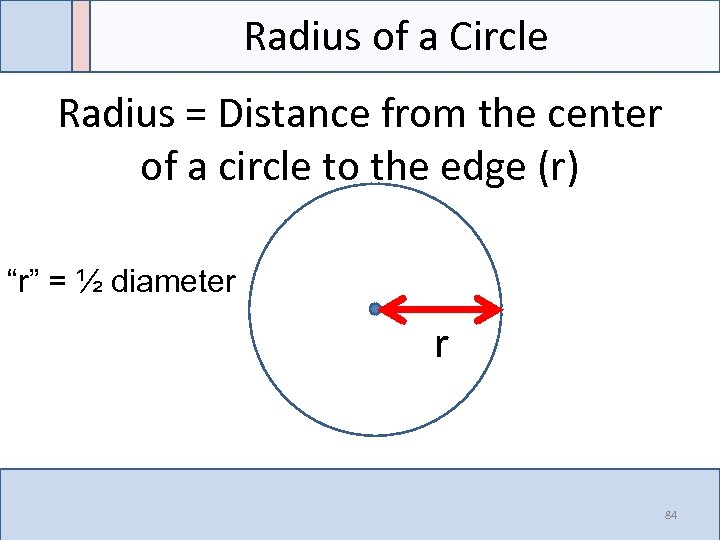 Radius of a Circle Radius = Distance from the center of a circle to the edge (r) “r” = ½ diameter r 84
Radius of a Circle Radius = Distance from the center of a circle to the edge (r) “r” = ½ diameter r 84
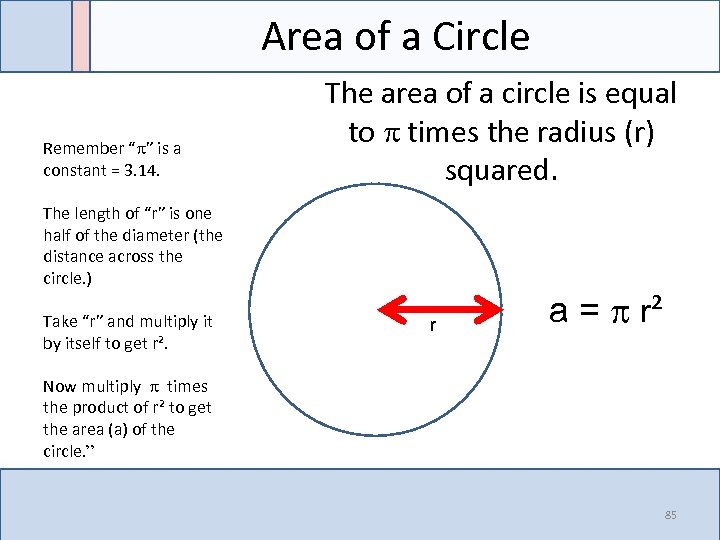 Area of a Circle Remember “ ” is a constant = 3. 14. The area of a circle is equal to times the radius (r) squared. The length of “r” is one half of the diameter (the distance across the circle. ) Take “r” and multiply it by itself to get r². r a = r² Now multiply times the product of r² to get the area (a) of the circle. ” 85
Area of a Circle Remember “ ” is a constant = 3. 14. The area of a circle is equal to times the radius (r) squared. The length of “r” is one half of the diameter (the distance across the circle. ) Take “r” and multiply it by itself to get r². r a = r² Now multiply times the product of r² to get the area (a) of the circle. ” 85
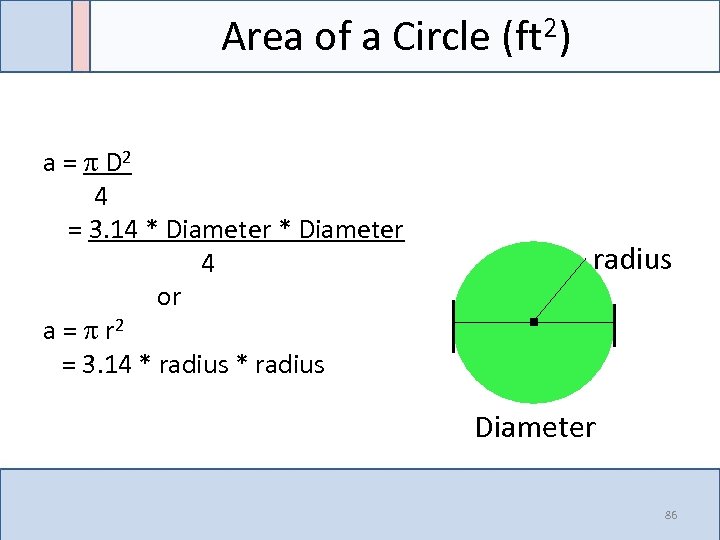 Area of a Circle (ft 2) radius . a = D 2 4 = 3. 14 * Diameter 4 or a = r 2 = 3. 14 * radius Diameter 86
Area of a Circle (ft 2) radius . a = D 2 4 = 3. 14 * Diameter 4 or a = r 2 = 3. 14 * radius Diameter 86
 Volume of a Cylinder (ft 3) v = D 2 * h h = height of the cylinder 4 = 3. 14 * Diameter * height 4 or v = r 2 * L = 3. 14 * radius * height 87
Volume of a Cylinder (ft 3) v = D 2 * h h = height of the cylinder 4 = 3. 14 * Diameter * height 4 or v = r 2 * L = 3. 14 * radius * height 87
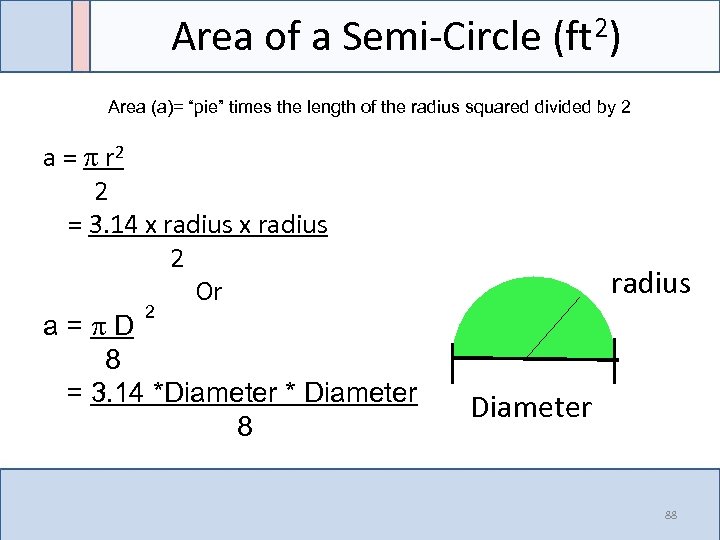 Area of a Semi-Circle (ft 2) Area (a)= “pie” times the length of the radius squared divided by 2 a = r 2 2 = 3. 14 x radius 2 Or 2 a= D 8 = 3. 14 *Diameter * Diameter 8 radius Diameter 88
Area of a Semi-Circle (ft 2) Area (a)= “pie” times the length of the radius squared divided by 2 a = r 2 2 = 3. 14 x radius 2 Or 2 a= D 8 = 3. 14 *Diameter * Diameter 8 radius Diameter 88
 Volume of 1/2 a Cylinder 3) (ft Volume = r 2 x h h = height of the cylinder 2 = 3. 14 x radius x height 2 or using diameter (D) Volume = D 2 x h 8 = 3. 14 x Diameter x height 8 89
Volume of 1/2 a Cylinder 3) (ft Volume = r 2 x h h = height of the cylinder 2 = 3. 14 x radius x height 2 or using diameter (D) Volume = D 2 x h 8 = 3. 14 x Diameter x height 8 89
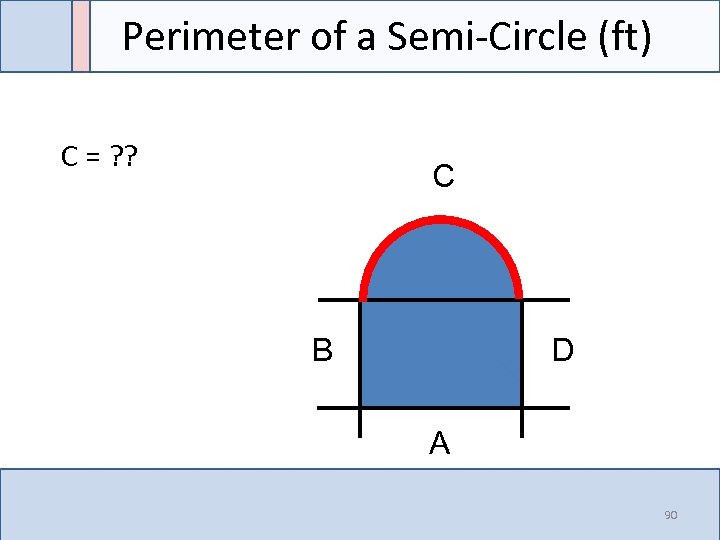 Perimeter of a Semi-Circle (ft) C = ? ? C B D A 90
Perimeter of a Semi-Circle (ft) C = ? ? C B D A 90
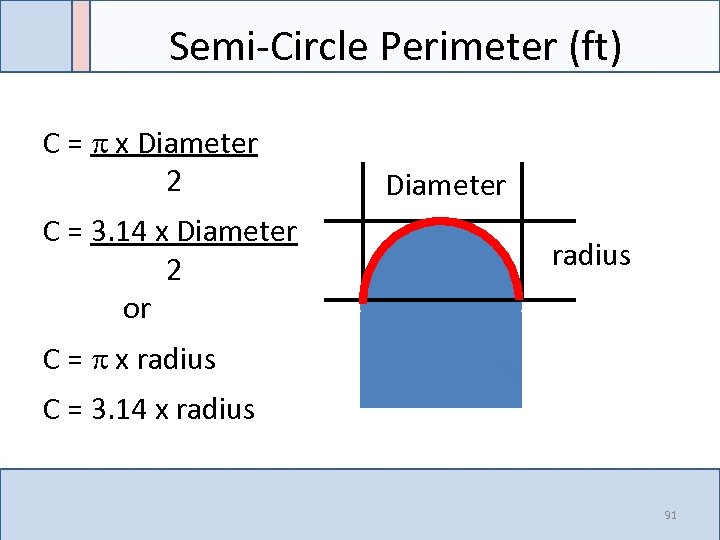 Semi-Circle Perimeter (ft) C = x Diameter 2 C = 3. 14 x Diameter 2 or Diameter radius C = x radius C = 3. 14 x radius 91
Semi-Circle Perimeter (ft) C = x Diameter 2 C = 3. 14 x Diameter 2 or Diameter radius C = x radius C = 3. 14 x radius 91
 Area by Component (ft 2) 92
Area by Component (ft 2) 92
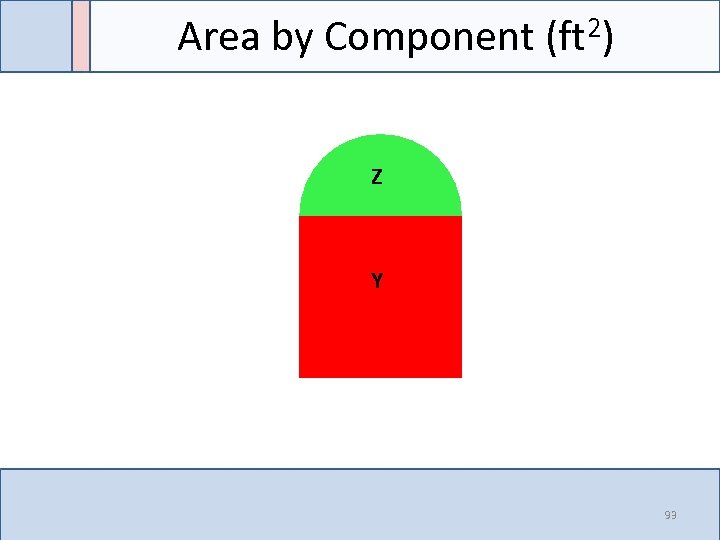 Area by Component (ft 2) Z Y 93
Area by Component (ft 2) Z Y 93
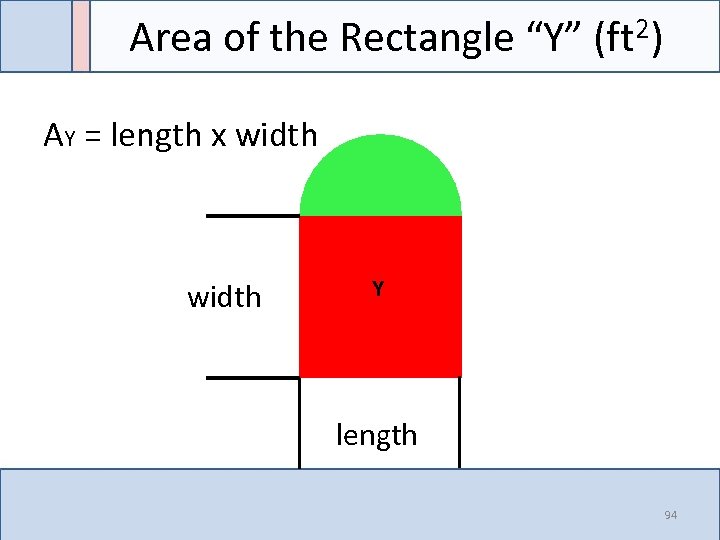 Area of the Rectangle “Y” (ft 2) AY = length x width Y length 94
Area of the Rectangle “Y” (ft 2) AY = length x width Y length 94
 Area of the Semi-Circle “Z” (ft 2) AZ = r 2 2 = 3. 14 x radius 2 or A Z = D 2 Diameter Z radius 8 = 3. 14 x Diameter 8 95
Area of the Semi-Circle “Z” (ft 2) AZ = r 2 2 = 3. 14 x radius 2 or A Z = D 2 Diameter Z radius 8 = 3. 14 x Diameter 8 95
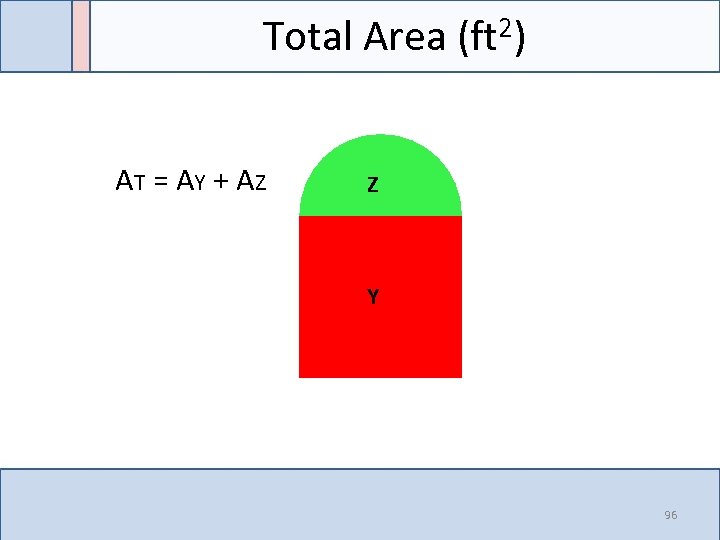 Total Area (ft 2) AT = A Y + A Z Z Y 96
Total Area (ft 2) AT = A Y + A Z Z Y 96
 Volume (ft 3) Know AY + AZ L = Length VY = A Y x L VZ = A Z x L VT = V Y + V Z Z Y 97
Volume (ft 3) Know AY + AZ L = Length VY = A Y x L VZ = A Z x L VT = V Y + V Z Z Y 97
 Semi-Circle Calculations -Your Turn- 98
Semi-Circle Calculations -Your Turn- 98
 Special Cases • Ducts • Tray Ceilings 99
Special Cases • Ducts • Tray Ceilings 99
 Duct Surface Area Rectangular Duct: Surface Area = 2 x (height + width) x length Round Duct: Surface Area = 3. 14 x Duct Diameter x length 100
Duct Surface Area Rectangular Duct: Surface Area = 2 x (height + width) x length Round Duct: Surface Area = 3. 14 x Duct Diameter x length 100
 Special Case – Tray Ceiling 101
Special Case – Tray Ceiling 101
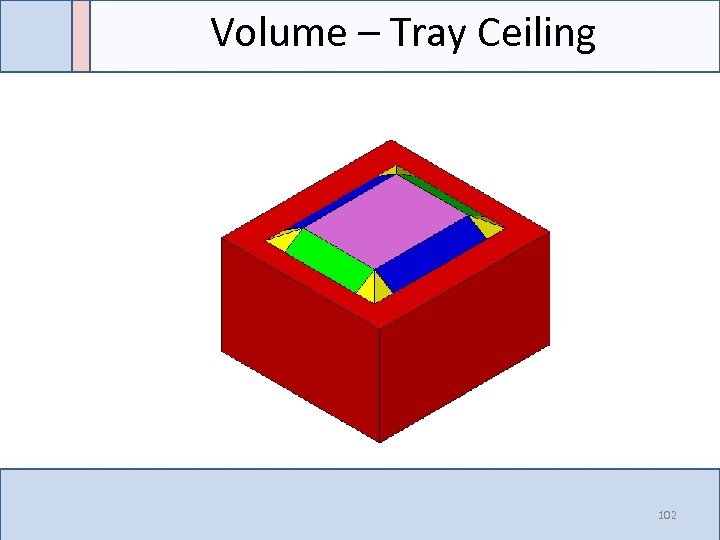 Volume – Tray Ceiling 102
Volume – Tray Ceiling 102
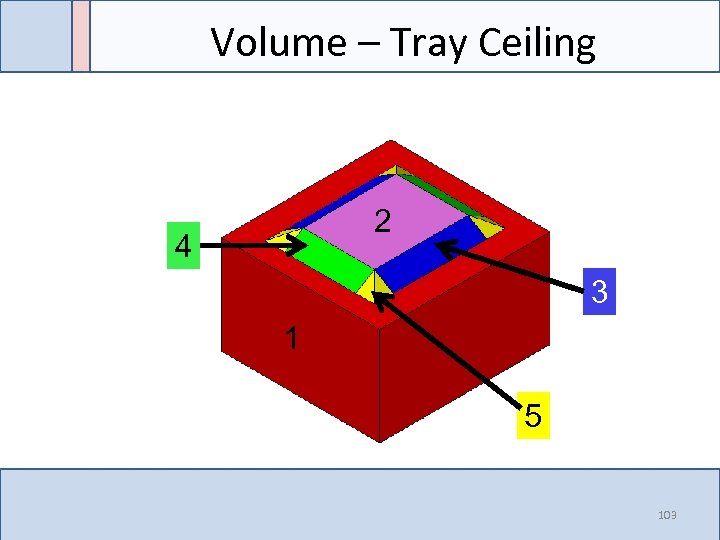 Volume – Tray Ceiling 2 4 3 1 5 103
Volume – Tray Ceiling 2 4 3 1 5 103
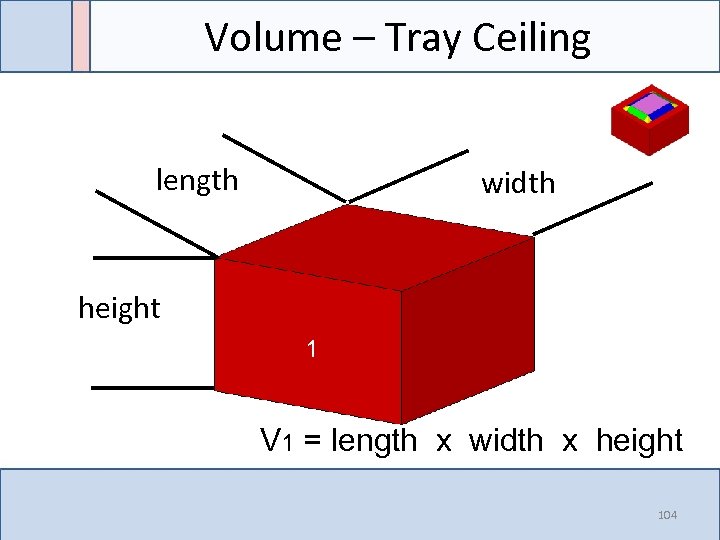 Volume – Tray Ceiling length width height 1 V 1 = length x width x height 104
Volume – Tray Ceiling length width height 1 V 1 = length x width x height 104
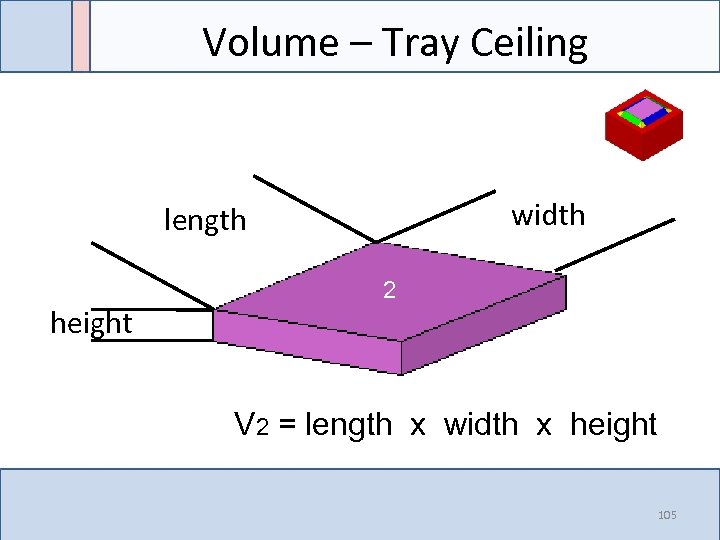 Volume – Tray Ceiling width length height 2 V 2 = length x width x height 105
Volume – Tray Ceiling width length height 2 V 2 = length x width x height 105
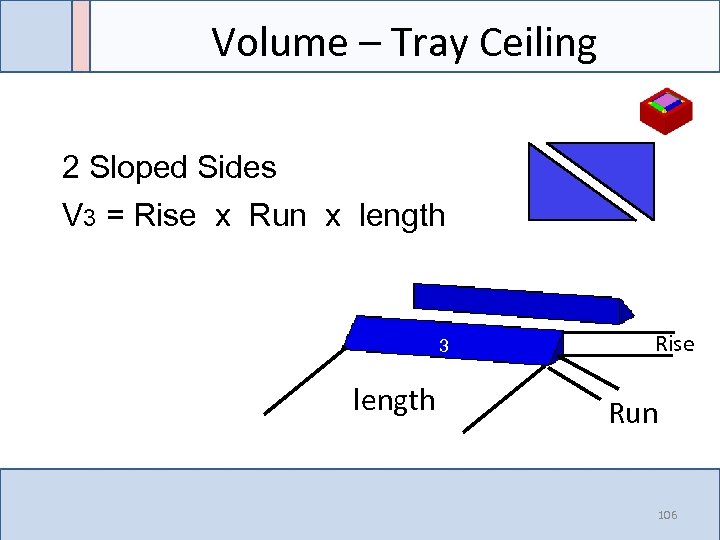 Volume – Tray Ceiling 2 Sloped Sides V 3 = Rise x Run x length 3 length Rise Run 106
Volume – Tray Ceiling 2 Sloped Sides V 3 = Rise x Run x length 3 length Rise Run 106
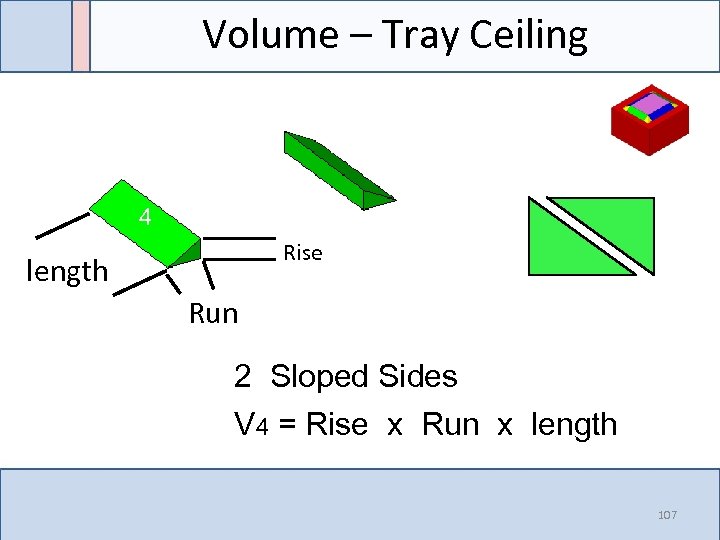 Volume – Tray Ceiling 4 Rise length Run 2 Sloped Sides V 4 = Rise x Run x length 107
Volume – Tray Ceiling 4 Rise length Run 2 Sloped Sides V 4 = Rise x Run x length 107
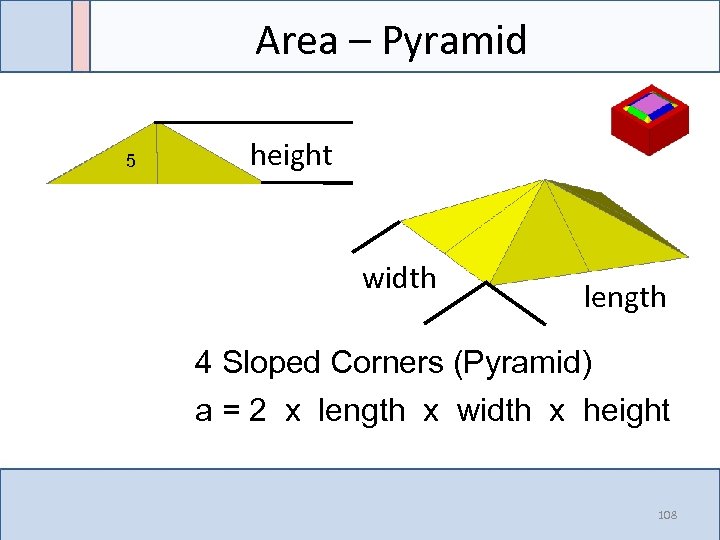 Area – Pyramid 5 height width length 4 Sloped Corners (Pyramid) a = 2 x length x width x height 108
Area – Pyramid 5 height width length 4 Sloped Corners (Pyramid) a = 2 x length x width x height 108
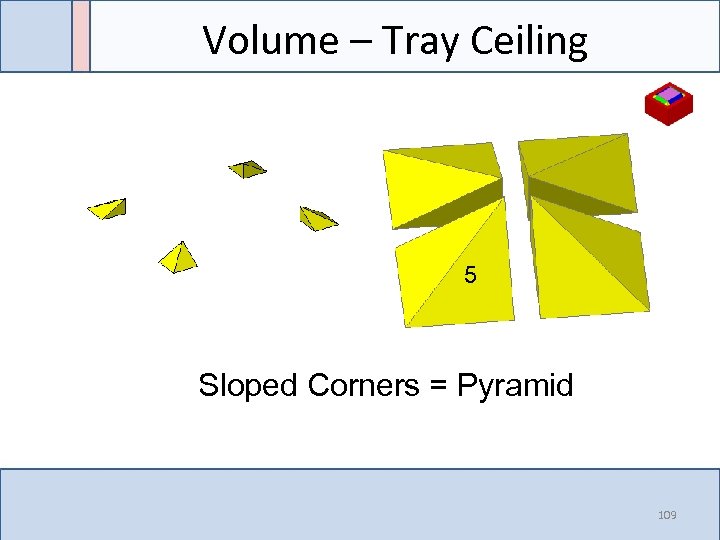 Volume – Tray Ceiling 5 Sloped Corners = Pyramid 109
Volume – Tray Ceiling 5 Sloped Corners = Pyramid 109
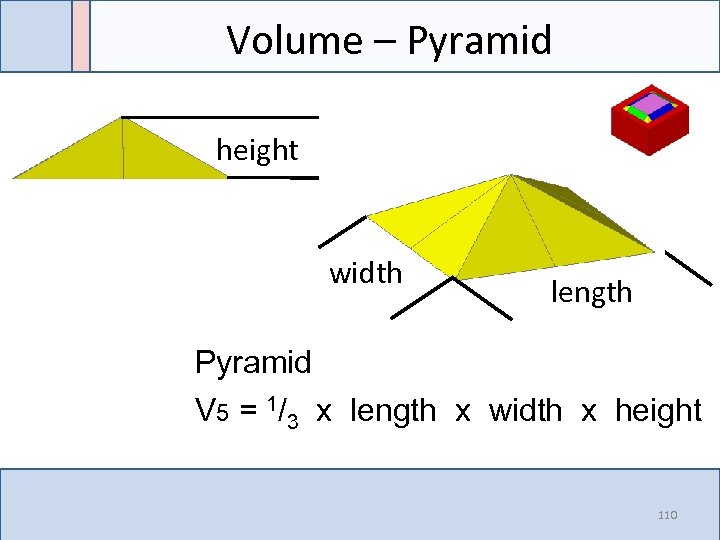 Volume – Pyramid height width length Pyramid V 5 = 1/3 x length x width x height 110
Volume – Pyramid height width length Pyramid V 5 = 1/3 x length x width x height 110
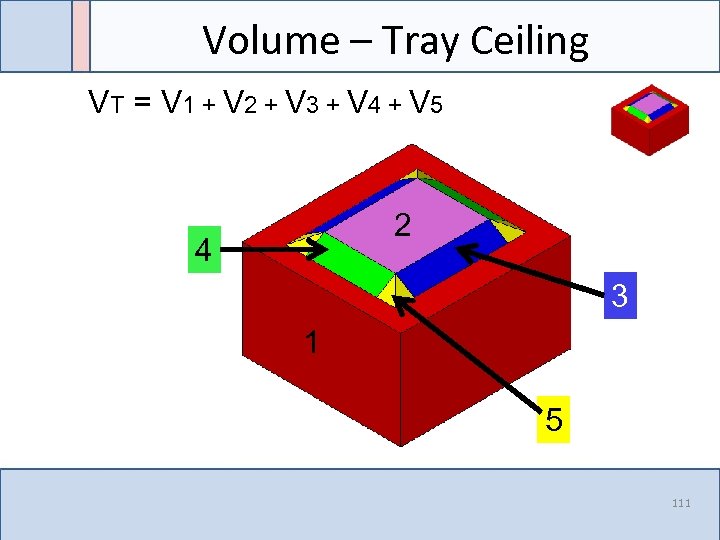 Volume – Tray Ceiling VT = V 1 + V 2 + V 3 + V 4 + V 5 2 4 3 1 5 111
Volume – Tray Ceiling VT = V 1 + V 2 + V 3 + V 4 + V 5 2 4 3 1 5 111
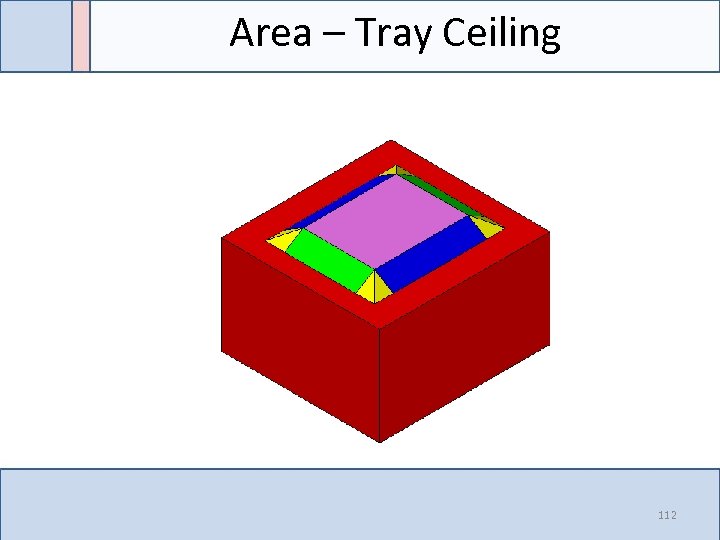 Area – Tray Ceiling 112
Area – Tray Ceiling 112
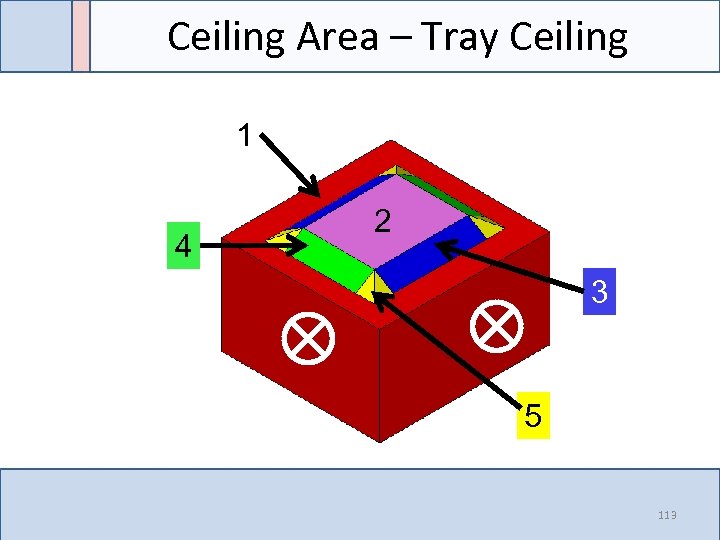 Ceiling Area – Tray Ceiling 1 4 2 3 5 113
Ceiling Area – Tray Ceiling 1 4 2 3 5 113
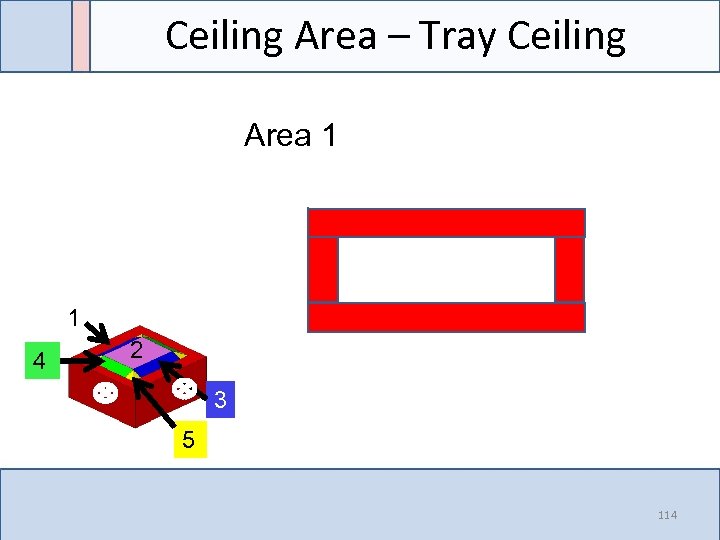 Ceiling Area – Tray Ceiling Area 1 1 4 2 3 5 114
Ceiling Area – Tray Ceiling Area 1 1 4 2 3 5 114
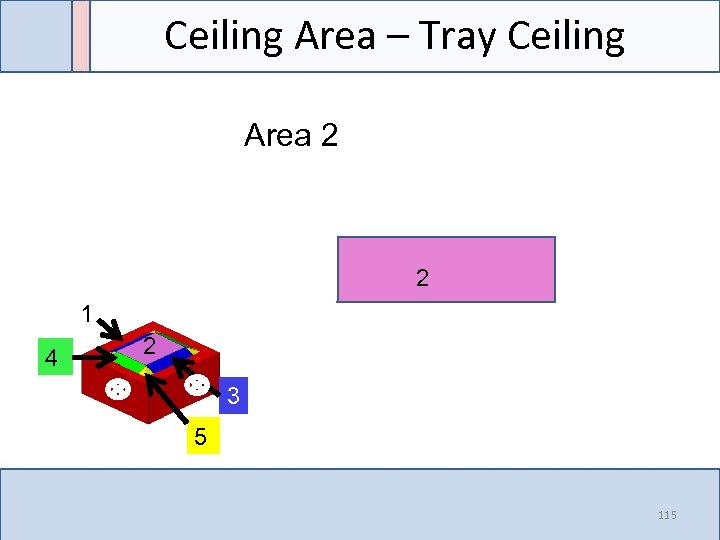 Ceiling Area – Tray Ceiling Area 2 2 1 4 2 3 5 115
Ceiling Area – Tray Ceiling Area 2 2 1 4 2 3 5 115
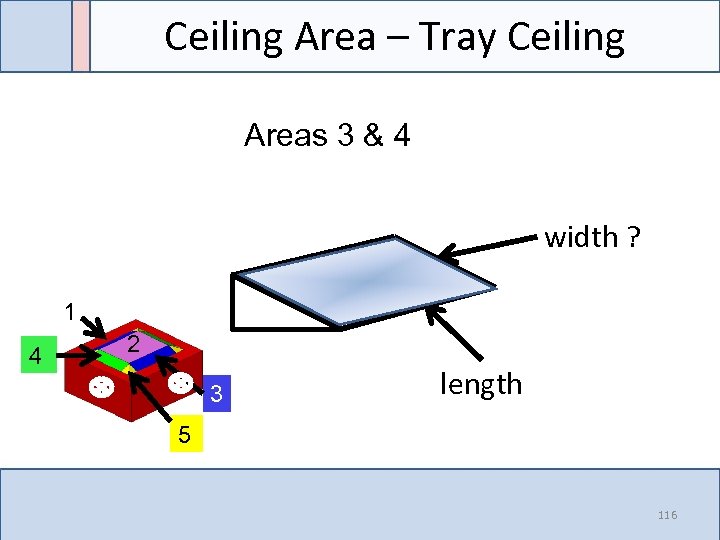 Ceiling Area – Tray Ceiling Areas 3 & 4 width ? 1 4 2 3 length 5 116
Ceiling Area – Tray Ceiling Areas 3 & 4 width ? 1 4 2 3 length 5 116
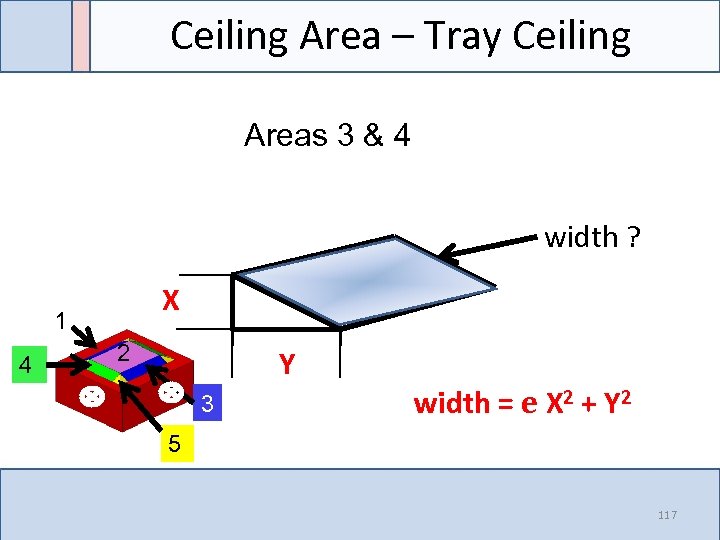 Ceiling Area – Tray Ceiling Areas 3 & 4 width ? X 1 4 2 Y 3 width = e X 2 + Y 2 5 117
Ceiling Area – Tray Ceiling Areas 3 & 4 width ? X 1 4 2 Y 3 width = e X 2 + Y 2 5 117
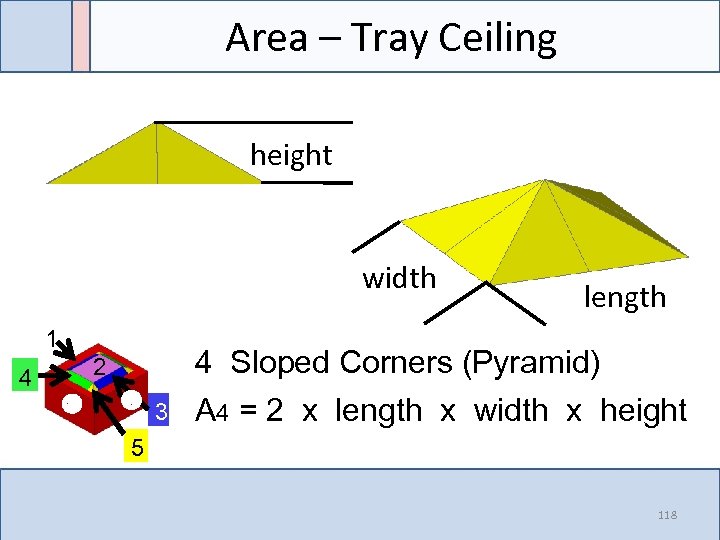 Area – Tray Ceiling height width 1 4 length 4 Sloped Corners (Pyramid) 2 3 A 4 = 2 x length x width x height 5 118
Area – Tray Ceiling height width 1 4 length 4 Sloped Corners (Pyramid) 2 3 A 4 = 2 x length x width x height 5 118


