3752e47917bc52536795eca6857e96fc.ppt
- Количество слайдов: 60
 MATH 685/ CSI 700/ OR 682 Lecture Notes Lecture 4. Least squares
MATH 685/ CSI 700/ OR 682 Lecture Notes Lecture 4. Least squares
 Method of least squares • Measurement errors are inevitable in observational and experimental sciences • Errors can be smoothed out by averaging over many cases, i. e. , taking more measurements than are strictly necessary to determine parameters of system • Resulting system is overdetermined, so usually there is no exact solution • In effect, higher dimensional data are projected into lower dimensional space to suppress irrelevant detail • Such projection is most conveniently accomplished by method of least squares
Method of least squares • Measurement errors are inevitable in observational and experimental sciences • Errors can be smoothed out by averaging over many cases, i. e. , taking more measurements than are strictly necessary to determine parameters of system • Resulting system is overdetermined, so usually there is no exact solution • In effect, higher dimensional data are projected into lower dimensional space to suppress irrelevant detail • Such projection is most conveniently accomplished by method of least squares
 Linear least squares
Linear least squares
 Data fitting
Data fitting
 Data fitting
Data fitting
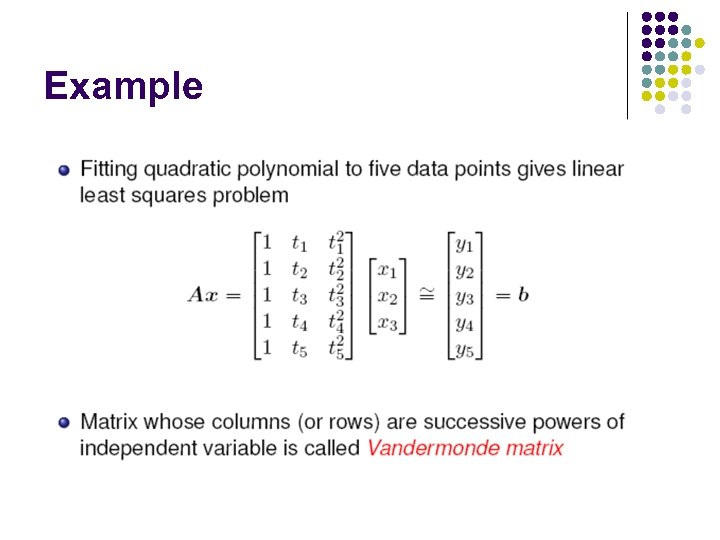 Example
Example
 Example
Example
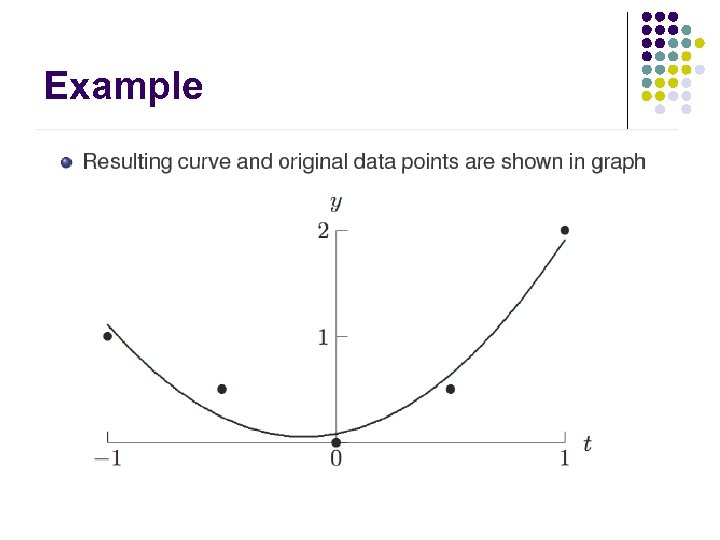 Example
Example
 Existence/Uniqueness
Existence/Uniqueness
 Normal Equations
Normal Equations
 Orthogonality
Orthogonality
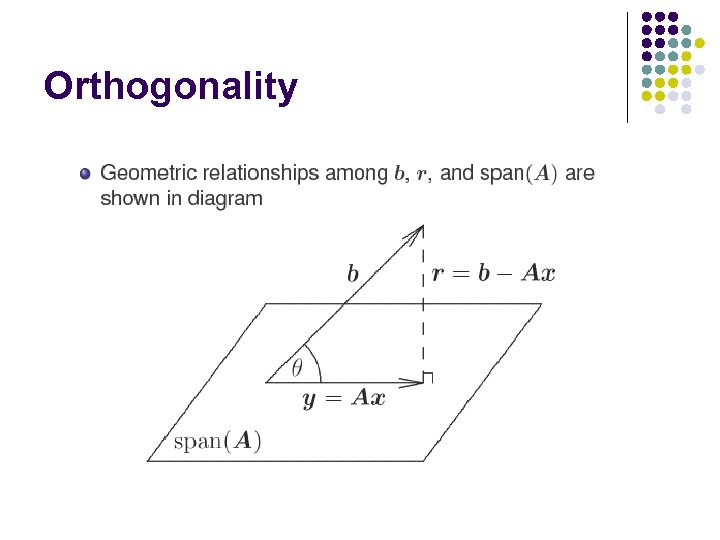 Orthogonality
Orthogonality
 Orthogonal Projector
Orthogonal Projector
 Pseudoinverse
Pseudoinverse
 Sensitivity and Conditioning
Sensitivity and Conditioning
 Sensitivity and Conditioning
Sensitivity and Conditioning
 Solving normal equations
Solving normal equations
 Example
Example
 Example
Example
 Shortcomings
Shortcomings
 Augmented system method
Augmented system method
 Augmented system method
Augmented system method
 Orthogonal Transformations
Orthogonal Transformations
 Triangular Least Squares
Triangular Least Squares
 Triangular Least Squares
Triangular Least Squares
 QR Factorization
QR Factorization
 Orthogonal Bases
Orthogonal Bases
 Computing QR factorization l To compute QR factorization of m × n matrix A, with m > n, we annihilate subdiagonal entries of successive columns of A, eventually reaching upper triangular form l Similar to LU factorization by Gaussian elimination, but use orthogonal transformations instead of elementary elimination matrices l Possible methods include l Householder transformations l Givens rotations l Gram-Schmidt orthogonalization
Computing QR factorization l To compute QR factorization of m × n matrix A, with m > n, we annihilate subdiagonal entries of successive columns of A, eventually reaching upper triangular form l Similar to LU factorization by Gaussian elimination, but use orthogonal transformations instead of elementary elimination matrices l Possible methods include l Householder transformations l Givens rotations l Gram-Schmidt orthogonalization
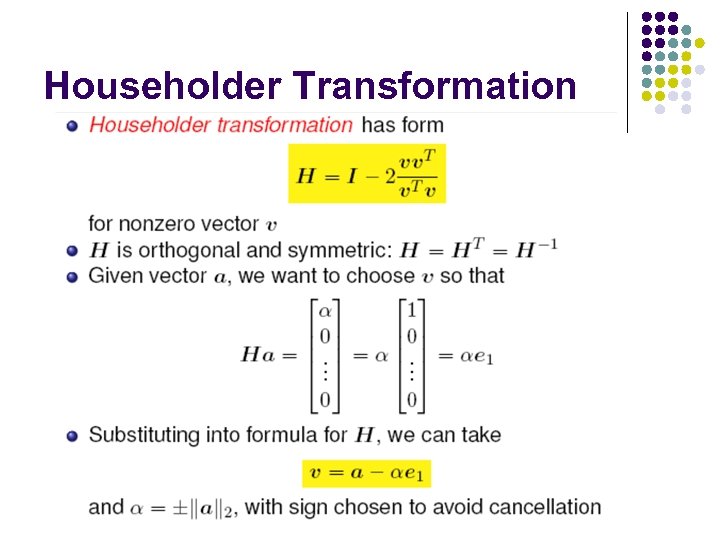 Householder Transformation
Householder Transformation
 Example
Example
 Householder QR factorization
Householder QR factorization
 Householder QR factorization
Householder QR factorization
 Householder QR factorization For solving linear least squares problem, product Q of Householder transformations need not be formed explicitly l R can be stored in upper triangle of array initially containing A l Householder vectors v can be stored in (now zero) lower triangular portion of A (almost) l Householder transformations most easily applied in this form anyway l
Householder QR factorization For solving linear least squares problem, product Q of Householder transformations need not be formed explicitly l R can be stored in upper triangle of array initially containing A l Householder vectors v can be stored in (now zero) lower triangular portion of A (almost) l Householder transformations most easily applied in this form anyway l
 Example
Example
 Example
Example
 Example
Example
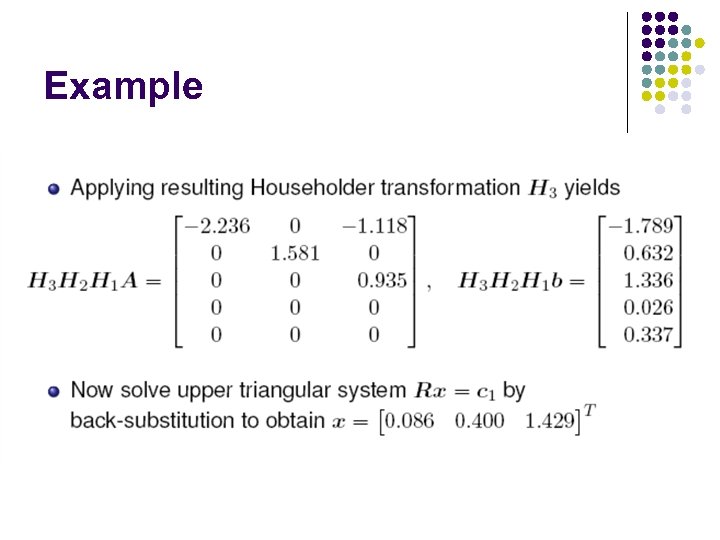 Example
Example
 Givens Rotations
Givens Rotations
 Givens Rotations
Givens Rotations
 Example
Example
 Givens QR factorization
Givens QR factorization
 Givens QR factorization Straightforward implementation of Givens method requires about 50% more work than Householder method, and also requires more storage, since each rotation requires two numbers, c and s, to define it l These disadvantages can be overcome, but requires more complicated implementation l Givens can be advantageous for computing QR factorization when many entries of matrix are already zero, since those annihilations can then be skipped l
Givens QR factorization Straightforward implementation of Givens method requires about 50% more work than Householder method, and also requires more storage, since each rotation requires two numbers, c and s, to define it l These disadvantages can be overcome, but requires more complicated implementation l Givens can be advantageous for computing QR factorization when many entries of matrix are already zero, since those annihilations can then be skipped l
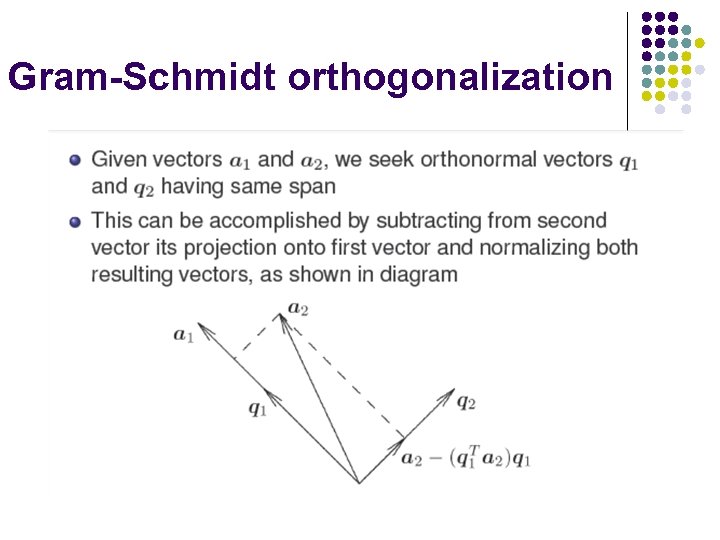 Gram-Schmidt orthogonalization
Gram-Schmidt orthogonalization
 Gram-Schmidt algorithm
Gram-Schmidt algorithm
 Modified Gram-Schmidt
Modified Gram-Schmidt
 Modified Gram-Schmidt QR factorization
Modified Gram-Schmidt QR factorization
 Rank Deficiency If rank(A) < n, then QR factorization still exists, but yields singular upper triangular factor R, and multiple vectors x give minimum residual norm l Common practice selects minimum residual solution x having smallest norm l Can be computed by QR factorization with column pivoting or by singular value decomposition (SVD) l Rank of matrix is often not clear cut in practice, so relative tolerance is used to determine rank l
Rank Deficiency If rank(A) < n, then QR factorization still exists, but yields singular upper triangular factor R, and multiple vectors x give minimum residual norm l Common practice selects minimum residual solution x having smallest norm l Can be computed by QR factorization with column pivoting or by singular value decomposition (SVD) l Rank of matrix is often not clear cut in practice, so relative tolerance is used to determine rank l
 Near Rank Deficiency
Near Rank Deficiency
 QR with Column Pivoting
QR with Column Pivoting
 QR with Column Pivoting
QR with Column Pivoting
 Singular Value Decomposition
Singular Value Decomposition
 Example: SVD
Example: SVD
 Applications of SVD
Applications of SVD
 Pseudoinverse
Pseudoinverse
 Orthogonal Bases
Orthogonal Bases
 Lower-rank Matrix Approximation
Lower-rank Matrix Approximation
 Total Least Squares l Ordinary least squares is applicable when right-hand side b is subject to random error but matrix A is known accurately l When all data, including A, are subject to error, then total least squares is more appropriate l Total least squares minimizes orthogonal distances, rather than vertical distances, between model and data l Total least squares solution can be computed from SVD of [A, b]
Total Least Squares l Ordinary least squares is applicable when right-hand side b is subject to random error but matrix A is known accurately l When all data, including A, are subject to error, then total least squares is more appropriate l Total least squares minimizes orthogonal distances, rather than vertical distances, between model and data l Total least squares solution can be computed from SVD of [A, b]
 Comparison of Methods
Comparison of Methods
 Comparison of Methods
Comparison of Methods
 Comparison of Methods
Comparison of Methods


