Math 307 Spring 2003 Hentzel Time 1 10

Math 307 Spring, 2003 Hentzel Time: 1: 10 -2: 00 MWF Room: 1324 Howe Hall Office 432 Carver Phone 515 -294 -8141 E-mail: hentzel@iastate. edu http: //www. math. iastate. edu/hentzel/class. 307. ICN Text: Linear Algebra With Applications, Second Edition Otto Bretscher

Wednesday, Jan 29 , Chapter 2. 2 Page 61 Problems 2, 18, 44 Main Idea: Matrices can stretch things out and twist them around. Key Words: Rotation, Dilation, Linear Transformation Goal: Look at a matrix and visualize what it does.

Previous Assignment: Page 48 Problems 32, 34, 42 Page 48 Problem 32: Find an nxn matrix A such that AX = 3 X for all X in Rn. ans: A = 3 I.

Page 48 Problem 34: Consider the transformation T from R 2 to R 2 that rotates any vector X through a given angle t in the counterclockwise direction. Find the matrix of T in terms of t. ans: A = | Cos[t] -Sin[t] | | Sin[t] Cos[t] |.

Page 48 Problem 42: When you represent a three-dimensional object graphically in the plane (on paper, the blackboard, or a computer screen), you have to transform spatial coordinates | x 1 | | x 2 | into plane coordinates | y 1 |. | x 3 | | y 2 | The simplest choice is a linear transformation, for example, the one given by the matrix | -1/2 1 0 0 | 1 |.

(a) Use this transformation to represent the unit cube with corner points | 0 1 0 1 1 | | 0 0 1 1 0 1 | | 0 0 0 1 1 1 | Include the images of the x 1, x 2, x 3 axes in your sketch. | -1/2 1 0 | | 0 1 0 1 1 | | -1/2 0 1 | | 0 0 1 1 0 1 | = | 0 0 0 1 1 1 | | 0 -1/2 1 0 0 1/2 1 -1/2 | 1 1/2 |

New Material: Definition: A linear transformation does just what any reasonable person would expect. These are (a) T(V+W) = T(V)+T(W) for all vectors V, W. (b) T(c. V) = c T(V) for all numbers c and all vectors V.

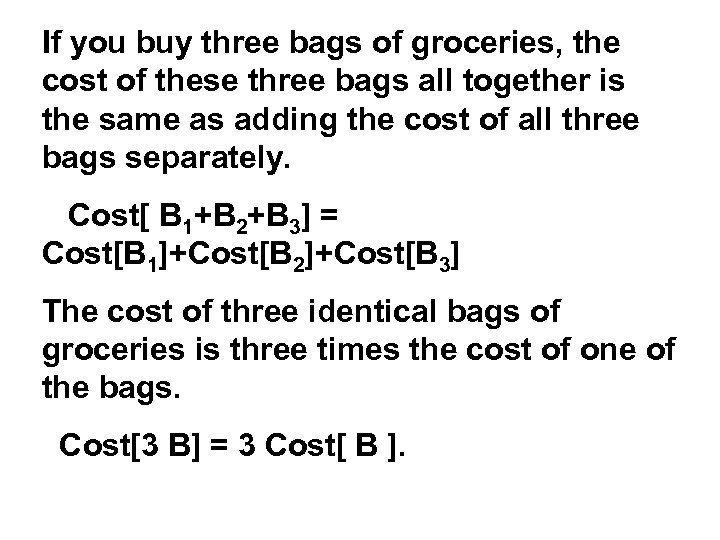If you buy three bags of groceries, the cost of these three bags all together is the same as adding the cost of all three bags separately. Cost[ B 1+B 2+B 3] = Cost[B 1]+Cost[B 2]+Cost[B 3] The cost of three identical bags of groceries is three times the cost of one of the bags. Cost[3 B] = 3 Cost[ B ].

Now you can argue that if you buy in quantities, then you can get things cheaper. Fine! Then the cost is not a linear function. Most processes are linear if the changes are not too large. For example: If you want to produce 10% more cars, you need 10% more labor and 10% more material.

In J. I. Case Company in Burlington, they made three models of crawler tractors, the 310, the 750, and the 1000. Their computer had a list of 20, 000 parts which were in the inventory. Whenever an order came in for a tractor, the computer would subtract the parts needed from the inventory. As one would suspect, the parts function is linear.

If they wanted to make: 3 of the 310, 5 of the 750, 2 of the 1000's, then: Parts(3 V 310+5 V 750+2 V 1000) = 3 Parts(V 310) + 5 Parts(V 750) + 2 Parts(V 1000)

The area of matrices limits itself to things which behave linearly. Show that this function is linear. | a | | a+b | T| b | = | b-c |. | c | First: What is | 2 | T | 3 | ? | 4 | | 5 | ans |-1 |. What is | 1 | T| -1 | ? | -1 | | 0 | ans | 0 |.

Part (i): We have to check that T(V+W) = T(V) + T(W) | a | | x | | a+x | T(| b | + | y | ) = T( | b+y | ) | c | | z | | c+z | = |a+x+b+y| = | a+b | + |x+y| |b+y-c-z| | b-c | |y-z| | a | | x | = T( | b | ) + T( | y | ). | c | | z |

Part (ii). We have to show that T(c. V) = c T(V). | x | | cx | T( c | y | ) = T( | cy | ) | z | | cz | |x| = |cx+cy| = c |x+y|= c T(|y|). |cy–cz| |y-z| |z|

Any linear function can be represented by a matrix. The matrix for T is gotten by evaluating the situation and writing down just what it has to be. First, Since T converts a vector of length three to a vector of length 2, T must be a 2 x 3 matrix. |a| | a+b | T| b | = | b - c | |c|

|a| T| b | = |c| |a+b| |b - c| T= |1 1 0| | 0 1 -1 | Check it with a general vector as follows | 1 1 0||a| |a+b| | 0 1 -1 | | b | = | b - c | |c|

Write the matrix for: | x | | 1 x + 2 y + z | f| y | = | 2 x + 5 y - z | | 5 x + 4 y +24 z | Notice that the matrix is just | | 1 | | 0 | | | f| 0 | f| 1 | f| 0 | | 1 | | = | | | 1 2 5 4 1 | -1 | 24 |

(a) Write the matrix for rotation of the x-y plane by 90 degrees. (b) Write the matrix for rotation of the x-y plane by 45 degrees. (c) Write the matrix for rotation of the x-y plane by 30 degrees.

What is the inverse for (a). What is the inverse for (b). What is the inverse for (c).

Rotation Dilation: |1 -1| = Sqrt[2]|1/Sqrt[2] -1/Sqrt[2]| |1 1| |1/Sqrt[2]| means it rotates through an angle theta where Cos[theta] = 1/Sqrt[2] and then stretches it by a factor of Sqrt[2].

Shear: There is a line L such that (1) L is left fixed (2) Things not on L are moved parallel to L. i. e. T(v) = v for all v on L. T(v)-v is parallel to L for v not on L.

Show that | | 1 0 1/2 1 | is a shear. | | a | ----> | a + 1/2 b | | b | For | a | to be fixed, b is zero. | b | Therefore the X-axis is fixed. T| a | - | a | = | 1/2 b | | 0 | Movement is parallel to the X-axis.

Suppose that U and W are perpendicular. That is: U. W = 0. Show that T[X] = X + (U. X) W is a shear parallel to W. T[k. W] = k. W + (U. k. W)W = k. W since U. W = 0. T[X]-X = (U. X) W Which is parallel to W.

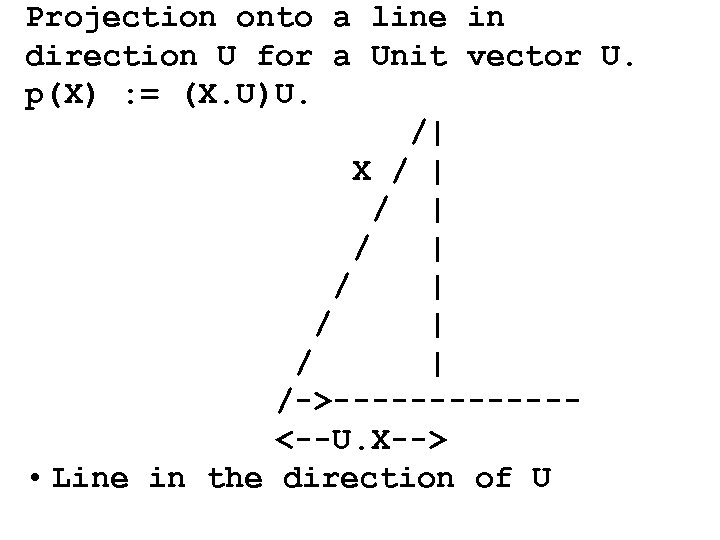Projection onto a line in direction U for a Unit vector U. p(X) : = (X. U)U. /| X / | / | / | /->------<--U. X--> • Line in the direction of U

Reflection in a direction U. X /. / // U/ f(X) : = 2 (X. U)U - X. f(U) = U If X is perpendicular to U, then X switches sign.

The matrix for a rotation is | Cos[t] -Sin[t] | | Sin[t] Cos[t] | The matrix for a reflection is | Cos[t] Sin[t] | | Sin[t] -Cos[t] | The matrix for a dilation is | c 0 | | 0 c |

Express the linear transformation | 6 8 | as a rotation followed | -8 6 | by a dilation. Notice that the matrix is of the form. 10 | 0. 6 0. 8 | | -0. 8 0. 6 | Rotation by Arc. Sin[-0. 8] = -53. 1301 degrees followed by a dilation with factor of 10.

Express the linear transformation | 12 5 | | 5 -12 | as a flip followed by a dilation. 13 | 12/13 5/13 | | 5/13 -12/13 | If Cos[theta] = 12/13, this is a flip about the line making the angle 1/2 theta. Then a dilation by the multiple of 13.

How do you tell them apart. | a -b | | a b | | b a | | b -a | rotation reflection You can view the reflection as first doing the rotation and then flipping the new y-axis.