Материалы по курсу! http: //ppsy. msk. ru/meth User: student, Password: hse Лекция 8. Обзор математических методов обработки данных психологических исследований Курс «Количественные и качественные методы исследования в психологии» Евгений Осин, НИУ ВШЭ, 2011
Основные вопросы • Проверка статистических гипотез: общая логика, размер эффекта, уровень значимости, мощность анализа. • Классификация математических методов и алгоритм выбора нужного метода. • Краткий обзор возможностей, ограничений и шагов наиболее часто используемых методов.
Для чего нам нужна статистика? • Результаты наших исследований переменные (случайные величины), полученные на ограниченной выборке. • Нас интересует, насколько достоверно по этим данным мы можем делать выводы о свойствах всей генеральной совокупности объектов (например, людей). • Статистические методы позволяют нам оценить эту достоверность количественно. • Статистические методы исходят из того, что наша выборка является случайной. Если она не такова, статистические методы могут вводить нас в заблуждение.
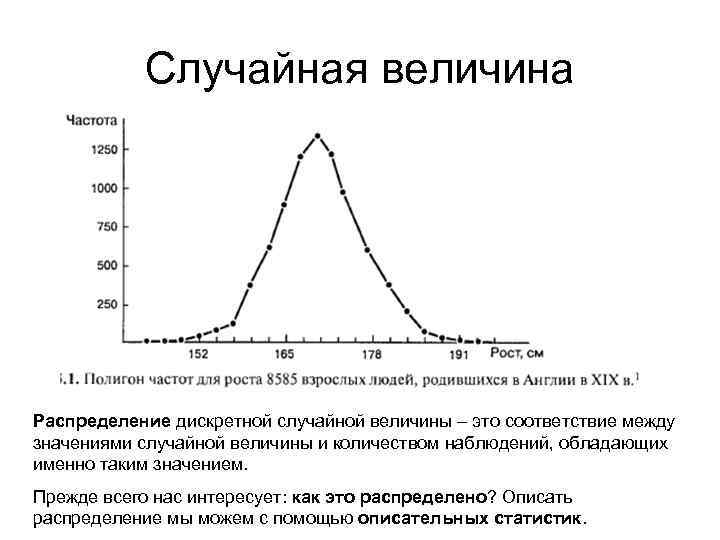Случайная величина Распределение дискретной случайной величины – это соответствие между значениями случайной величины и количеством наблюдений, обладающих именно таким значением. Прежде всего нас интересует: как это распределено? Описать распределение мы можем с помощью описательных статистик.
Выбор статистик • Выбор статистик, прежде всего, определяется видом шкалы, по которой измерена интересующая нас переменная: – – шкала наименований (номинативная); шкала порядков; интервальная шкала; шкала отношений. • Методы для шкал интервалов и отношений, как правило, не различаются. Для простоты эти шкалы можно называть просто количественными (исходя из того, что балл по шкале соответствует количеству признака).
Как описать распределение? • Описательные статистики: – меры центральной тенденции: • среднее (арифметическое); • медиана (ровно половина наблюдений меньше этого значения, половина -- больше); • мода (самое распространённое значение переменной в выборке); – меры разброса: • размах (разница между максимальным и минимальным значением); • межквартильный размах (разница между значением, меньше которого ровно 25% наблюдений и значением, меньше которого ровно 75% наблюдений); • дисперсия (средний квадрат отклонения значений переменной от среднего); • стандартное отклонение (корень из дисперсии).
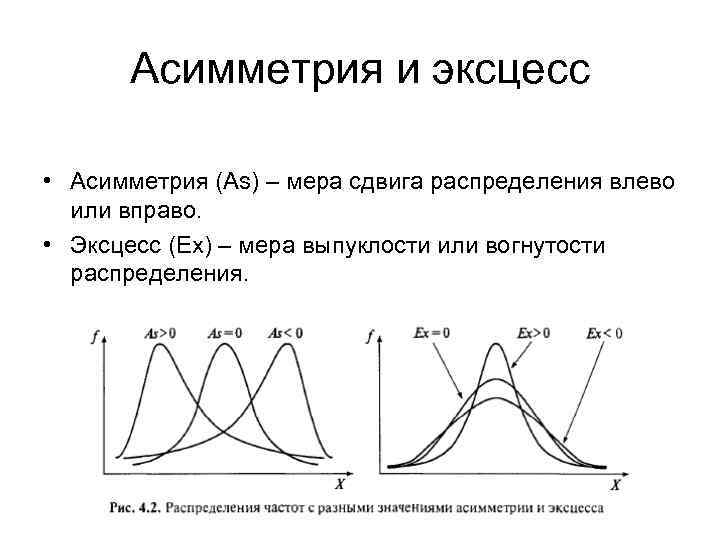Асимметрия и эксцесс • Асимметрия (As) – мера сдвига распределения влево или вправо. • Эксцесс (Ex) – мера выпуклости или вогнутости распределения.
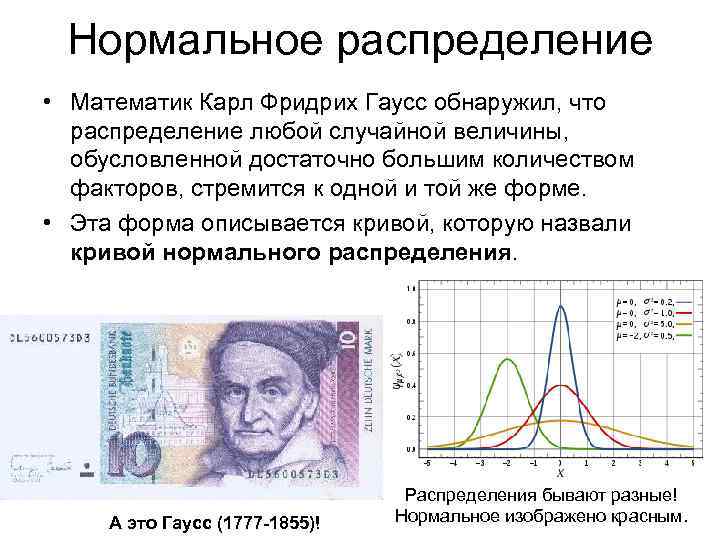Нормальное распределение • Математик Карл Фридрих Гаусс обнаружил, что распределение любой случайной величины, обусловленной достаточно большим количеством факторов, стремится к одной и той же форме. • Эта форма описывается кривой, которую назвали кривой нормального распределения. А это Гаусс (1777 -1855)! Распределения бывают разные! Нормальное изображено красным.
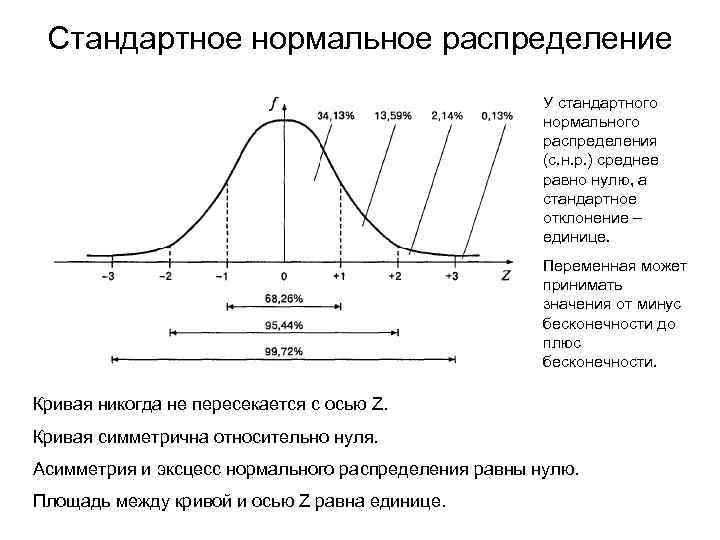Стандартное нормальное распределение У стандартного нормального распределения (с. н. р. ) среднее равно нулю, а стандартное отклонение – единице. Переменная может принимать значения от минус бесконечности до плюс бесконечности. Кривая никогда не пересекается с осью Z. Кривая симметрична относительно нуля. Асимметрия и эксцесс нормального распределения равны нулю. Площадь между кривой и осью Z равна единице.
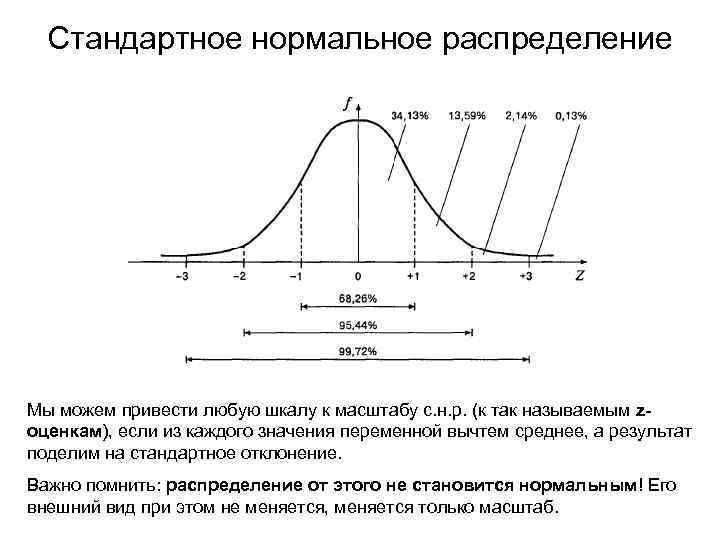Стандартное нормальное распределение Мы можем привести любую шкалу к масштабу с. н. р. (к так называемым zоценкам), если из каждого значения переменной вычтем среднее, а результат поделим на стандартное отклонение. Важно помнить: распределение от этого не становится нормальным! Его внешний вид при этом не меняется, меняется только масштаб.
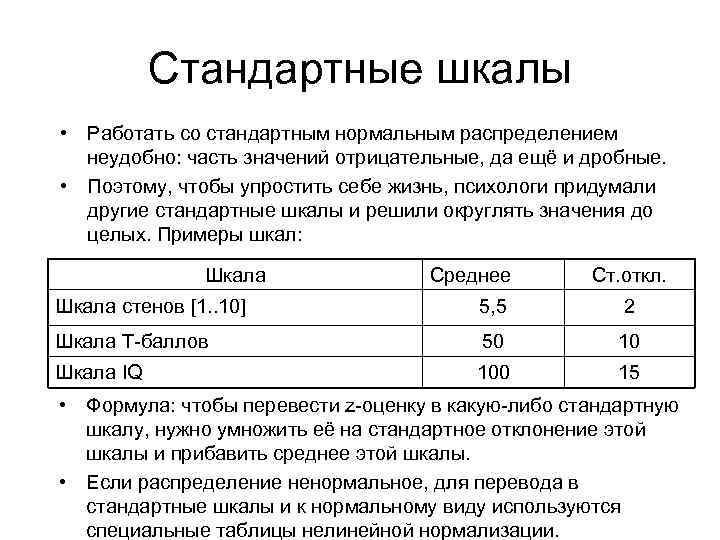Стандартные шкалы • Работать со стандартным нормальным распределением неудобно: часть значений отрицательные, да ещё и дробные. • Поэтому, чтобы упростить себе жизнь, психологи придумали другие стандартные шкалы и решили округлять значения до целых. Примеры шкал: Шкала Среднее Ст. откл. Шкала стенов [1. . 10] 5, 5 2 Шкала T-баллов 50 10 Шкала IQ 100 15 • Формула: чтобы перевести z-оценку в какую-либо стандартную шкалу, нужно умножить её на стандартное отклонение этой шкалы и прибавить среднее этой шкалы. • Если распределение ненормальное, для перевода в стандартные шкалы и к нормальному виду используются специальные таблицы нелинейной нормализации.
Статистический критерий • Математическая процедура, которая позволяет нам оценить, насколько достоверно по выборке мы можем делать вывод о генеральной совокупности. • Результатом является уровень значимости, отражающий достоверность нашего вывода. • На основе уровня значимости мы принимаем решение о том, какой вывод сделать.
Виды статистических критериев • Если распределение какой-либо величины соответствует нормальному, нам достаточно знать его параметры: среднее и стандартное отклонение. • Статистики, которые исходят из предположения о нормальности распределения, мы называем параметрическими. В случаях отклонений распределения от нормальности, они могут нас обманывать! • Статистики, которые не имеют лишних иллюзий и адекватно работают с распределениями, отличающимися от нормального, мы называем непараметрическими.
Логика статистической проверки гипотез • H 1: «Альтернативная гипотеза» : эффект есть. • H 0: «Нулевая гипотеза» : нет оснований говорить о том, что эффект есть. • Чтобы выбрать между ними, мы ориентируемся на уровень значимости:
Виды гипотез • Гипотезы бывают: – направленные, или односторонние: они предполагают направление различий, например: • в среднем, тревожность у женщин выше, чем у мужчин. – ненаправленные, или двусторонние: когда направление ожидаемых различий нам неизвестно, например: • средний уровень тревожности у женщин отличается от среднего уровня у мужчин.
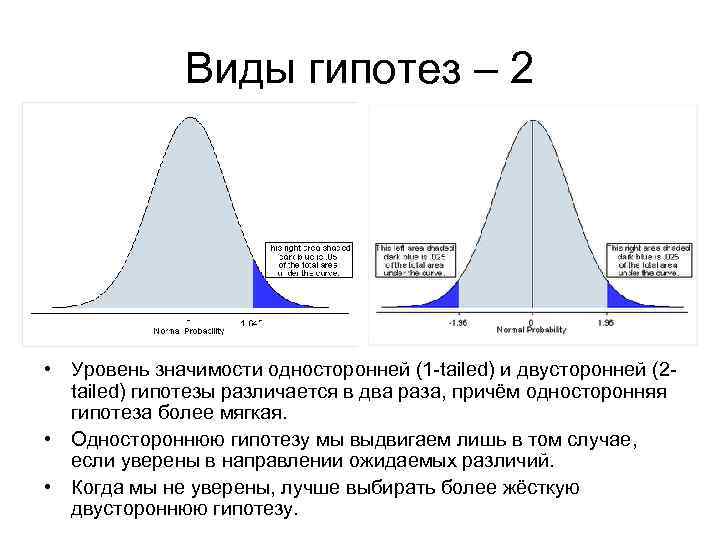Виды гипотез – 2 • Уровень значимости односторонней (1 -tailed) и двусторонней (2 tailed) гипотезы различается в два раза, причём односторонняя гипотеза более мягкая. • Одностороннюю гипотезу мы выдвигаем лишь в том случае, если уверены в направлении ожидаемых различий. • Когда мы не уверены, лучше выбирать более жёсткую двустороннюю гипотезу.
Два вида ошибок принятии статистических решений Верная на самом деле (в генеральной совокупности) гипотеза: H 0 Результат проверки гипотезы на выборке: H 1 H 0 верно принята H 0 неверно отвергнута (Ошибка первого рода, её вероятность – уровень значимости α) H 1 H 0 неверно принята (Ошибка второго рода, её вероятность -- β) H 0 верно отвергнута
Статистическая мощность анализа • Уровень значимости: вероятность того, что мы приняли гипотезу H 1, которая на самом деле неверна. • Статистическая мощность анализа (1β): вероятность того, что мы на выборке примем гипотезу H 1, если на самом деле она верна (= шанс обнаружить эффект, если он на самом деле есть).
Что такое размер эффекта? • Примеры размеров эффекта: – r: коэффициент корреляции Пирсона; – d: различие между средними (Коэна). Тип р. э. | r | «слабый» < 0. 3 «средний» 0. 3 … 0. 7 «сильный» 0. 7 … 1 | d | около 0. 3 около 0. 6 0. 8 и выше • Пример 1. Корреляция между приёмом аспирина и снижением риска сердечного приступа: r = 0. 034, r 2 = 0. 0012. Но это значит, что 34 человека из 1000 могут предотвратить приступ, принимая аспирин. • Пример 2. Эффективность психотерапии: r = 0. 39.
Статистическая мощность анализа • Зависит от… – объёма выборки: чем он больше, тем она выше; – размера эффекта: чем он сильнее, тем она выше; – от используемого статистического критерия: для разных статистических критериев, проверяющих одну и ту же гипотезу, она будет разной. • Является критерием для определения объёма выборки с учётом размера ожидаемого эффекта. • Важно! Только высокая мощность (0, 95 и выше) даёт нам возможность делать достоверный вывод о том, что искомый эффект отсутствует (верна H 0). • При недостаточной статистической мощности подобный вывод является необоснованным (правильный вывод: мы не обнаружили эффект, но не можем сказать, есть он или нет).
Зависимость статистической мощности от размера выборки
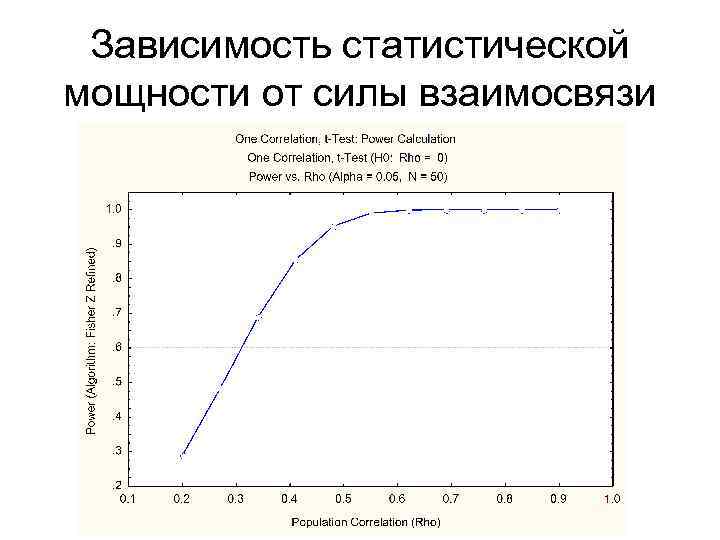Зависимость статистической мощности от силы взаимосвязи
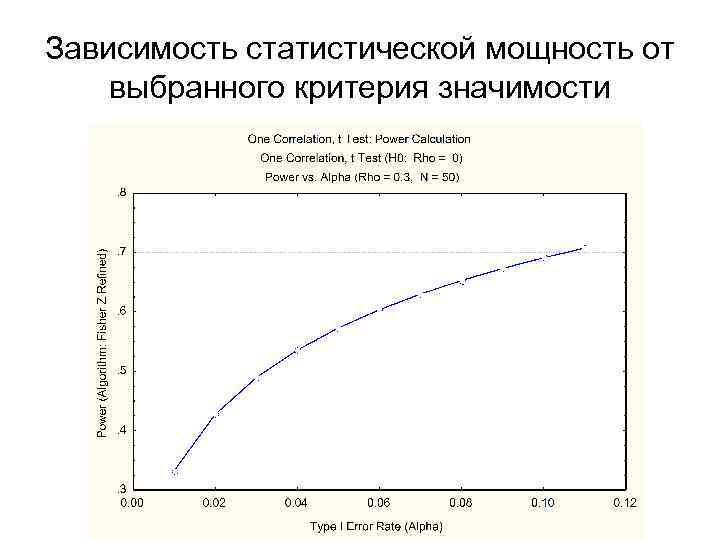Зависимость статистической мощность от выбранного критерия значимости
Виды математических методов • Мы классифицируем их: – по задаче: • сравнение эмпирического (наблюдаемого) распределения с теоретическим (ожидаемым); • сравнение эмпирических распределений между собой (сравнение выборок); • поиск взаимосвязей между переменными. – по типу шкал исходных данных; – по наличию предположения о нормальном распределении (параметрические и непараметрические); – по наличию проверки гипотез: эксплораторные и конфирматорные (вторые включают проверку гипотез).
Критерии для сравнения теоретического распределения с эмпирическим • Исходные данные: один столбец значений, которые принимает переменная. • (Столбец «Фамилия» необязателен: это просто идентификатор наблюдения). Фамилия Гусев Лебедев Орлов Воронов Уточкин Напиток вино пиво вино Пример вопроса: являются ли напитки одинаково популярными? Гипотезы: H 1: распределение отличается от равномерного, H 0: нет оснований говорить об отличии…
Алгоритм выбора критерия • Переменная номинативная, 2 градации биномиальный критерий. [Например: значения переменной – орел и решка. Вопрос, равновесна ли монета соответствует ли распр-е равномерному? ] • Переменная номинативная, >2 градаций критерий хи-квадрат. [Например: значения переменной – выбор политической партии человеком. Являются ли партии одинаково предпочитаемыми? ] • Переменная порядковая и выше критерии Колмогорова-Смирнова, хи-квадрат. [Например: соответствует ли распределение IQ в группе студентов Вышки нормальному закону? ]
Критерии для сравнения двух распределений • Исходные данные: два столбца значений, которые принимает одна и та же переменная в разных замерах (зависимые выборки) или две разные переменные. Пол Мужской Женский Напиток вино пиво вино Пример вопроса: являются ли распределения предпочтений напитков у М и Ж одинаковыми? Гипотезы: H 1: распределения извлечены из разных ген. совокупностей, H 0: нет оснований говорить о том, что это так.
Алгоритм выбора критерия Сравнение 2 или нескольких эмпирических распределений: одна (независимая) переменная номинативная, а вторая (зависимая)… номинативная (анализ таблиц сопряжённости) 2 градации признака -> таблицы 2 x 2 независимые выборки: хи-квадрат с поправкой на непрерывность, точное значение вероятности Фишера зависимые выборки: критерий Мак-Нимара более 2 градаций признака – критерий хи-квадрат порядковая (непараметрические методы сравнения выборок) независимые выборки: критерий Манна-Уитни зависимые выборки: критерий Уилкоксона независимые выборки: критерий Краскала-Уоллиса зависимые выборки: критерий хи-квадрат Фридмана количественная (параметрические методы сравнения выборок) 1 независимая переменная: независимые выборки: t-критерий Стьюдента для незав. выб. , одномерная однофакторная ANOVA зависимые выборки: t-критерий Стьюдента для зав. выб. , однофакторная ANOVA с повторными изм. если 2 и более независимых переменных многофакторная ANOVA если 2 и более зависимых переменных многомерная ANOVA 2 и более независимых количественных, зависимая номинативная: дискриминантный анализ
Зависимые и независимые выборки • Зависимые выборки – это выборки, наблюдения в которых попарно соответствуют другу. Примеры зависимых выборок: – пары замеров одной и той же переменной в разные моменты времени (до и после тренинга); – значения одного и того же признака у близнецов, либо или у мужей и у их жён. • Выборки, где нет такого соответствия являются независимыми.
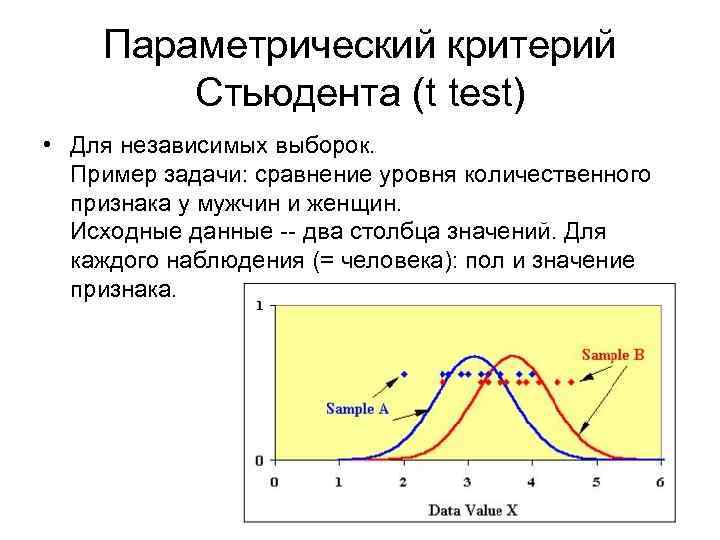Параметрический критерий Стьюдента (t test) • Для независимых выборок. Пример задачи: сравнение уровня количественного признака у мужчин и женщин. Исходные данные -- два столбца значений. Для каждого наблюдения (= человека): пол и значение признака.
Кто такой Стьюдент? • На самом деле этого человека звали совсем иначе. • Этот статистик работал на пивоварнях Гиннесса и по условиям контракта все результаты его работы принадлежали компании. • Поэтому он публиковал свои работы под псевдонимом «Стьюдент» и под ним и вошёл в историю.
Параметрический критерий Стьюдента (t test) • Для зависимых выборок. Пример задачи: сравнение уровня количественного признака у испытуемых до и после воздействия. Исходные данные -- два столбца значений. Для каждого наблюдения (= человека): значение признака при первом и втором замере.
Параметрический критерий Стьюдента (t test) • Параметрический критерий Стьюдента исходит из предположения о нормальности распределений в обеих выборках. Если распределение отличается от нормального, лучше использовать непараметрический критерий. • Классический критерий Стьюдента исходит из предположения о равенстве дисперсий в обеих выборках. • Но в SPSS есть и версия Стьюдента для выборок с неравными дисперсиями: если дисперсии не равны [а это проверяет тест Ливена: он значим не равны], надо смотреть именно на эту версию.
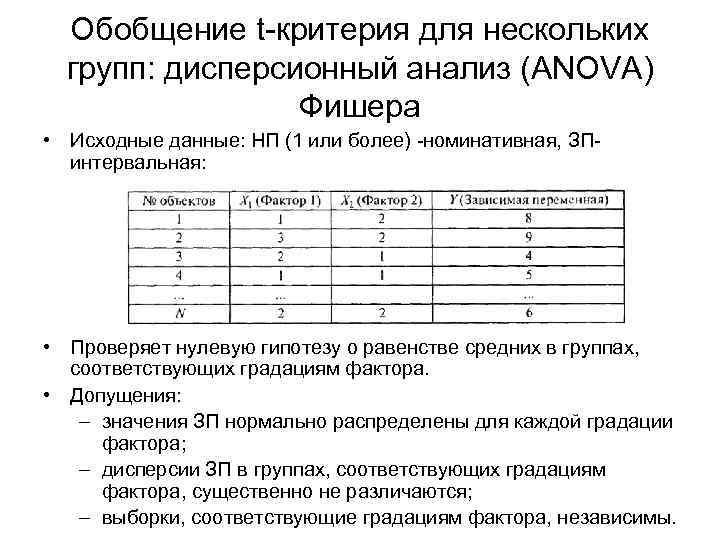Обобщение t-критерия для нескольких групп: дисперсионный анализ (ANOVA) Фишера • Исходные данные: НП (1 или более) -номинативная, ЗПинтервальная: • Проверяет нулевую гипотезу о равенстве средних в группах, соответствующих градациям фактора. • Допущения: – значения ЗП нормально распределены для каждой градации фактора; – дисперсии ЗП в группах, соответствующих градациям фактора, существенно не различаются; – выборки, соответствующие градациям фактора, независимы.
Виды анализа в ANOVA • Однофакторная ANOVA (1 -way): 1 НП, 1 ЗП • Многофакторная ANOVA (2+-way): 2 и более НП, 1 ЗП; можно проверять гипотезы о взаимодействии факторов • ANOVA с повторными измерениями (Repeated Measures): 1 из факторов (НП) – время. • MANOVA: 2 и более ЗП • ANCOVA: ANOVA с учётом побочных переменных (ковариатов)
Результаты ANOVA • Показатели значимости и масштаба основных эффектов и эффектов взаимодействия. • Пример: связь интеллекта с социальным статусом у здоровых и больных детей (В. Н. Дружинин).
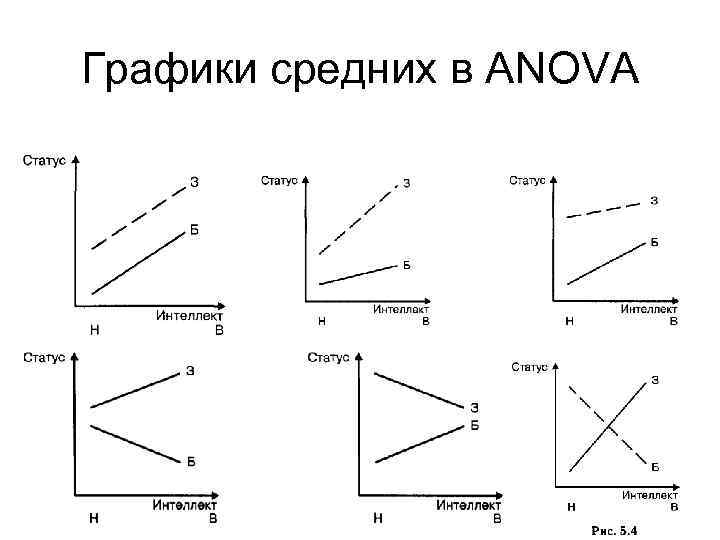Графики средних в ANOVA
Поиск взаимосвязей Обнаружение взаимосвязей однородных переменных 2 переменные (корреляции): две номинативные: см. выше – критерии для таблиц сопряжённости 2 x 2, фи Гилфорда номинативная и порядковая: бисериальная корреляция две порядковые: непараметрический коэфф. корр. Спирмена количественные: параметрический коэфф. корр. Пирсона регрессионный анализ более 2 переменных номинативные: деревья классификации, кластерный анализ порядковые: кластерный анализ количественные: факторный анализ, многомерное шкалирование, множественная регрессия, анализ надёжности
«Коэффициент корреляции» • Корреляционный анализ: семейство методов для проверки гипотез о наличии взаимосвязей между парами переменных, которые могут измеряться по различным шкалам много разных коэффициентов корреляции, количественно несопоставимых. • Чаще всего под словосочетанием «коэффициент корреляции» имеется в виду коэффициент корреляции r Пирсона. Карл Пирсон (1857 -1936) описал распределение хи-квадрат
Коэффициент корреляции Пирсона: формула • Ко-вариация, или показатель совместного изменения двух переменных вычисляется как сумма произведений отклонений от средних для каждой пары значений x и y: cov (x; y) = SUM((x – xср)(y – yср)). • Коэффицент корреляции – это стандартизованный коэффициент ковариации (делённый на произведение стандартных отклонений σx и σy): r (x; y) = cov (x; y) / (σx σy).
Коэффициент корреляции Пирсона • Количественный показатель выраженности взаимосвязи между двумя переменными, которые: – измерены по интервальной шкале; – нормально распределены. • Является адекватной мерой только для линейной взаимосвязи. • r Пирсона отражает силу взаимосвязи и лежит в пределах: -1 = максимально сильная обратная связь; 0 = связь отсутствует; +1 = максимально сильная прямая связь. • r Пирсона неаддитивны: чтобы складывать или усреднять корреляции, нужно предварительно перевести их в z-оценки с помощью преобразования Фишера, а после нужной операции – обратно в r
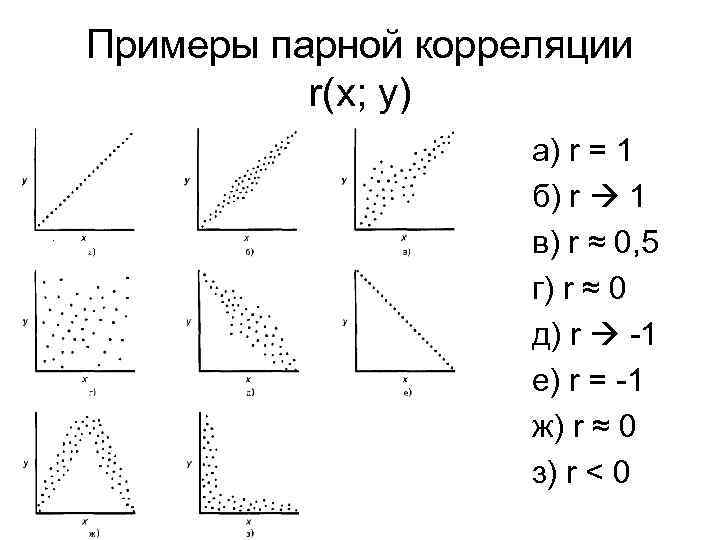Примеры парной корреляции r(x; y) а) r = 1 б) r 1 в) r ≈ 0, 5 г) r ≈ 0 д) r -1 е) r = -1 ж) r ≈ 0 з) r < 0
Уровень значимости • Уровень значимости (p, α) коэффициента корреляции отражает достоверность полученной взаимосвязи. • Уровень значимости – это вероятность того, что гипотеза о наличии взаимосвязи (H 1) неверна (= того, что сделав вывод о наличии связи, мы ошибёмся). • Для принятия гипотезы о наличии связи в психологии и социальных науках принят уровень значимости p≤ 0, 05 (1 шанс ошибки из 20): – – – p > 0, 1 : нет оснований делать вывод о взаимосвязи; 0, 05 < p ≤ 0, 1 : взаимосвязь на уровне тенденции; 0, 01 < p ≤ 0, 05: взаимосвязь достоверна на ур. зн. p ≤ 0, 05; 0, 001< p ≤ 0, 01: взаимосвязь достоверна на ур. зн. p ≤ 0, 01; p ≤ 0, 001 : взаимосвязь достоверна на уровне p ≤ 0, 001.
Уровень значимости • Достоверность взаимосвязи зависит: – от её силы (чем больше r по модулю, тем больше шансов, что он будет значим); – от объёма выборки (чем больше выборка, тем больше шансов, что r будет значим). • на очень маленьких выборках даже для сильных взаимосвязей значимость может не достичь приемлемого уровня; • на очень больших выборках даже очень слабые (и потому практически бессмысленные) взаимосвязи могут оказаться значимыми.
Артефакты • Объединение двух выборок с различающимися средними по обеим переменным может приводить к возникновению ложных корреляций на объединённой выборке проверять наличие различий в средних и в характере и степени взаимосвязи перед объединением. • Корреляция двух переменных может объясняться влиянием третьей переменной (пример: у детей размер ноги и IQ связаны друг с другом, а реальная причина – связь обеих переменных с возрастом) расчёт частной корреляции. • Наличие выбросов (наблюдений, существенно отклоняющихся от общих закономерностей) в данных на небольших выборках может приводить к появлению ложных корреляций или к снижению значений коэффициента корреляции проверка на нормальность, анализ графика разброса. • Низкая надёжность наблюдаемых переменных приводит к снижению коэффициента корреляции коррекция аттенюации.
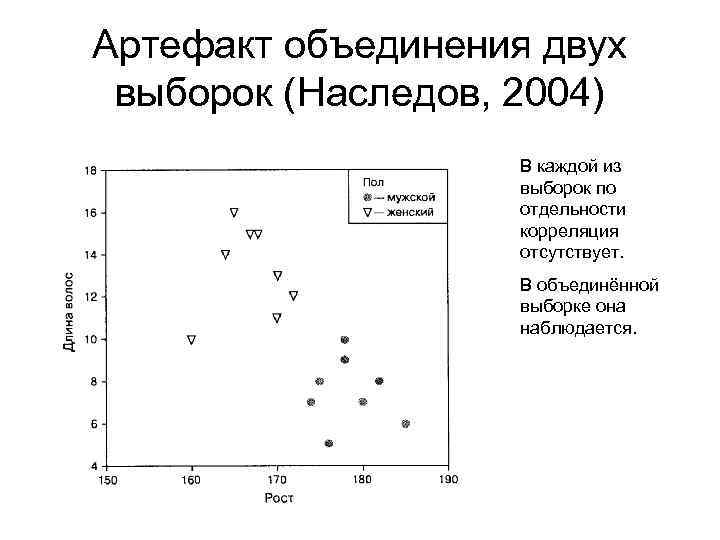Артефакт объединения двух выборок (Наследов, 2004) В каждой из выборок по отдельности корреляция отсутствует. В объединённой выборке она наблюдается.
Частная корреляция (пример А. Д. Наследова)
Что причина, а что следствие? S_ESTEEM OPTIM_US GRADE 4 S_ESTEEM 1. 0000 0. 3008 0. 1879 OPTIM_US GRADE 4 1. 0000 0. 2617 1. 0000 S_ESTEEM = Самооценка OPTIM_US = Оптимизм GRADE 4 = Средний балл за четверть по 4 предметам Школьники, N=234
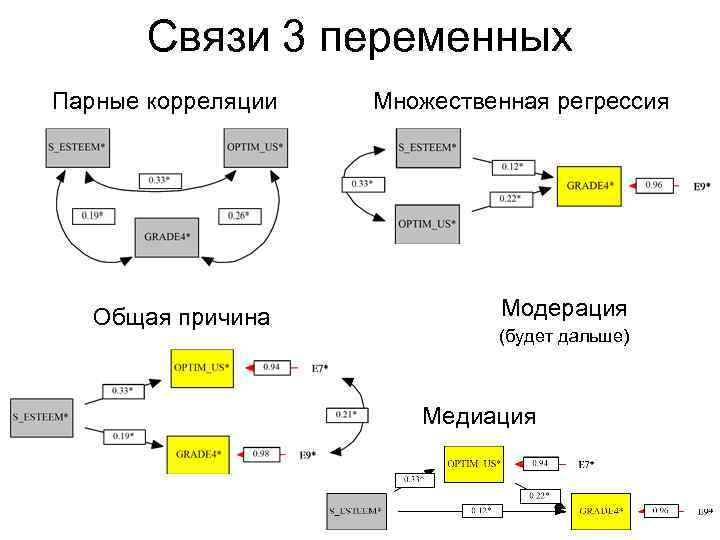Связи 3 переменных Парные корреляции Общая причина Множественная регрессия Модерация (будет дальше) Медиация
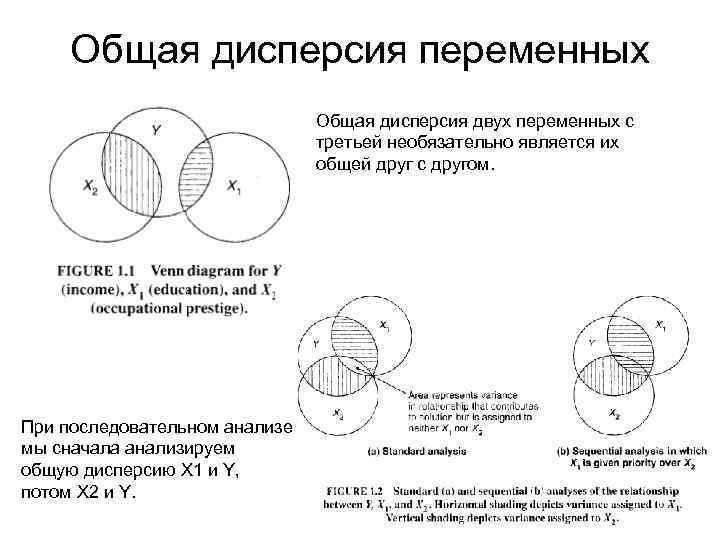Общая дисперсия переменных Общая дисперсия двух переменных с третьей необязательно является их общей друг с другом. При последовательном анализе мы сначала анализируем общую дисперсию X 1 и Y, потом X 2 и Y.
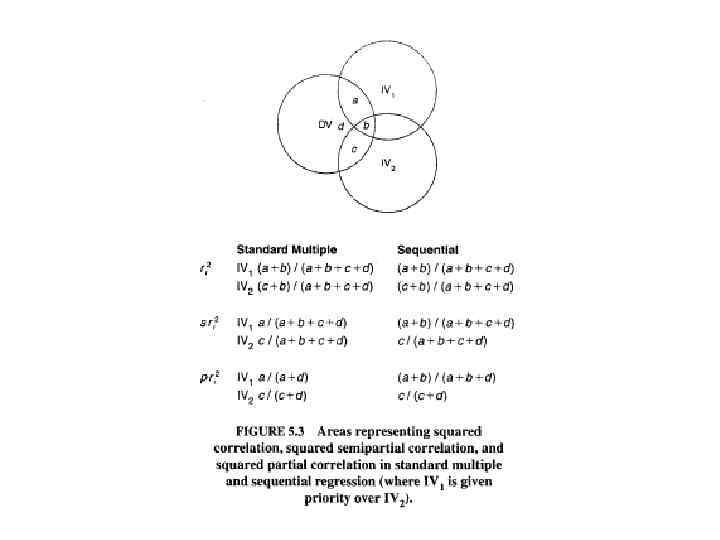
Математическое моделирование связей более двух переменных • Связь ряда независимых переменных с одной зависимой: регрессия. • Связи нескольких независимых и зависимых переменных друг с другом: – путевой анализ; – конфирматорный факторный анализ.
Многомерные методы • • Регрессионные модели Путевой анализ Эксплораторный факторный анализ Конфирматорный факторный анализ и моделирование линейными структурными уравнениями • Кластерный анализ
Регрессия • Множественная регрессия: несколько независимых переменных (порядковая/интервальная шкала), одна зависимая переменная (интервальная шкала) • Задача: построение уравнения, позволяющего предсказывать значения зависимой переменной на основе независимых и оценка достоверности предсказания
Регрессия • Допущения: нормальность распределений НП и ЗП, отсутствие мультиколлинеарности. • Мультиколлинеарность: ситуация, когда переменная чрезмерно коррелирует с другими (tolerance<. 20). Такие переменные необходимо исключать.
Регрессия • Результат: – регрессионное уравнение с коэффициентами (сырыми и стандартизованными); – уровень значимости для каждого предиктора (независимой переменной) и регрессионной модели в целом; – доля дисперсии зависимой переменной, объясняемой этим набором предикторов (R -квадрат).
Пошаговая регрессия • Независимые переменные включаются не все сразу, а по отдельности: – прямая пошаговая: независ. переменные добавляются в уравнение по одной до тех пор, пока происходит значимый прирост Rквадрат; – обратная пошаговая: все независ. переменные включаются в уравнение и удаляются по одной до тех пор, пока Rквадрат не начинает значимо падать.
Иерархическая регрессия • Пошаговая регрессия, где пользователь определяет последовательность добавления или удаления переменных на каждом шаге. • Используется для проверки значимости связи набора переменных при контроле других переменных (переменные, которые необходимо проконтролировать, задаются на первом шаге).
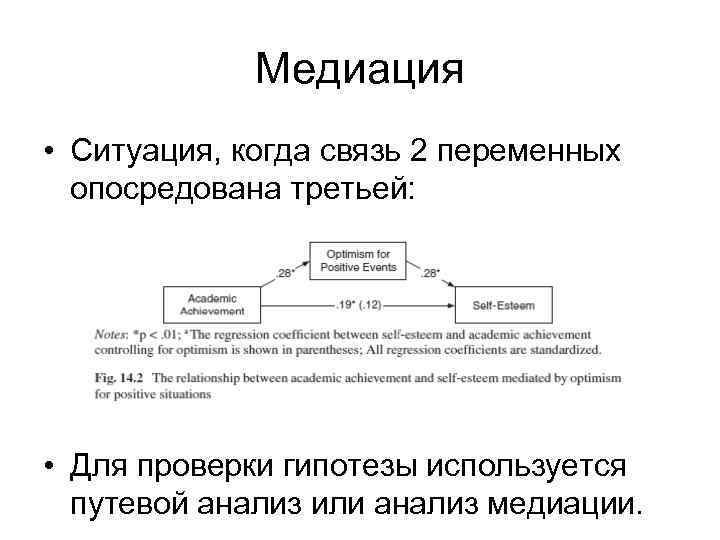Медиация • Ситуация, когда связь 2 переменных опосредована третьей: • Для проверки гипотезы используется путевой анализ или анализ медиации.
Модерация • Ситуация, когда сила или характер связи двух переменных X и Y зависит от значений третьей (модератора M). – Например: у мужчин связь X и Y прямая, у женщин – обратная. • Для проверки гипотезы используется: – ANOVA, где X и M являются факторами (модерация = эффект взаимодействия факторов); – Иерархическая пошаговая регрессия: на 1 шаге включаются X и M, на 2 шаге добавляется их произведение X*M. Если оно является значимым предиктором = есть модерация.
Путевой анализ • Путевой анализ позволяет одновременно оценить взаимосвязи нескольких наблюдаемых (измеренных) переменных друг с другом. • Можно рассматривать его как множественную регрессию с несколькими зависимыми переменными и несколькими уровнями независимых.
Путевой анализ
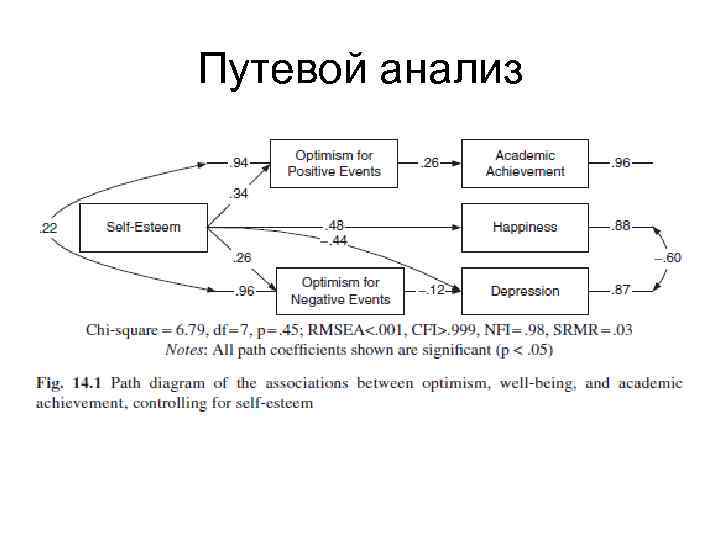Путевой анализ • Проблема: одной и той же системе переменных могут быть одинаково адекватны разные путевые модели (например, с разным направлением связей). • Решение: выбирать модель на основе теории, помня о том, что направленные связи между переменными в модели не позволяют нам судить о причинах и следствиях.
Эксплораторный ФА • Задача: поиск латентных переменных, объясняющих общую дисперсию наблюдаемых переменных. • Типичные задачи в психологии: – выявление структуры связей пунктов опросника (=> формирование шкал); – выявление структуры связей шкал одного или нескольких опросников (=> поиск вторичных факторов). • На входе: набор интервальных переменных (на практике часто используют порядковые).
Эксплораторный ФА • Допущения: используется матрица корреляций Пирсона, => допущения те же: • интервальная шкала (или хотя бы порядковая, но не бинарная! – для бинарной нужен редкий непараметрический вариант ФА); • нормальное распределение всех переменных; • учитываются только линейные взаимосвязи. • Выборка: как правило, необходимо не менее 5 наблюдений на каждую переменную. Но это зависит от доли ошибки в дисперсии исходных переменных: – если это сырые пункты (= в данных много шума), то нужно больше испытуемых для получения хорошей модели; – если шкалы (= малая доля ошибки измерения), не так много.
Эксплораторный ФА • На выходе: – матрица факторных нагрузок (степень связи каждой наблюдаемой переменной с каждым фактором); – доля всей дисперсии переменных, объясняемой каждым фактором и моделью в целом; – для каждой переменной – доля её дисперсии, вошедшая в факторную модель (общность). • Ограничения: – не оценивается дисперсия ошибки переменных.
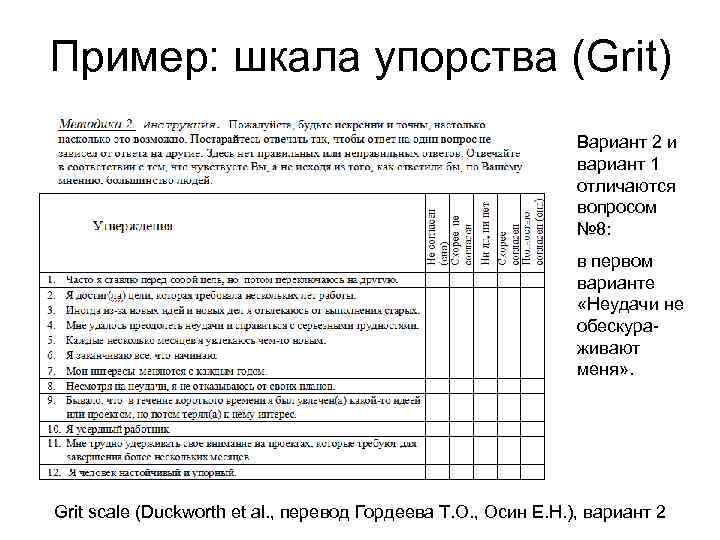Пример: шкала упорства (Grit) Вариант 2 и вариант 1 отличаются вопросом № 8: в первом варианте «Неудачи не обескураживают меня» . Grit scale (Duckworth et al. , перевод Гордеева Т. О. , Осин Е. Н. ), вариант 2
Матрица факторных нагрузок F 1 F 2 Var 1 0. 73 -0. 23 1. Часто я ставлю перед собой цель, но потом переключаюсь на другую. Var 2 0. 02 0. 46 2. Я достиг(ла) цели, которая требовала нескольких лет работы. Var 3 0. 75 -0. 10 3. Иногда из-за новых идей и новых дел я отвлекаюсь от выполнения старых. Var 4 -0. 04 0. 67 4. Мне удалось преодолеть неудачи и справиться с серьезными трудностями. Var 5 0. 62 0. 29 5. Каждые несколько месяцев я увлекаюсь чем-то новым. Var 6 -0. 50 0. 53 6. Я заканчиваю все, что начинаю. Var 7 0. 64 0. 07 7. Мои интересы меняются с каждым годом. Var 8 0. 04 0. 17 8. Неудачи не обескураживают меня. Var 9 0. 48 -0. 05 9. Бывало, что в течение короткого времени я был увлечен(а) какойто идеей или проектом, но потом терял(а) к нему интерес. Var 10 -0. 27 0. 77 10. Я усердный работник. Var 11 0. 63 -0. 25 11. Мне трудно удерживать свое внимание на проектах, которые требуют для завершения более нескольких месяцев. Var 12 -0. 17 0. 65 12. Я человек настойчивый и упорный. СЗ 2. 86 2. 20 % 0. 24 0. 18
Эксплораторный ФА: шаг 1 • Выбор исходных переменных: – желательно иметь не менее 3 индикаторов (наблюдаемых переменных) на каждый латентный фактор; – факторная структура будет яснее, если количество переменных на каждый фактор и степень их связи будут сходными (иначе при взаимосвязанных факторах более «мощные» факторы перетянут на себя переменные из более слабых).
Эксплораторный ФА: шаг 2 • Выбор количества факторов для вращения: – критерий Кайзера (по умолчанию): соб. зн. > 1 (часто не попадает в точку); – критерий Кеттелла: точка излома на графике соб. знач. ; – по доле объясняемой дисперсии (но какой она должна быть? -- это зависит от доли ошибки в исходных переменных…).
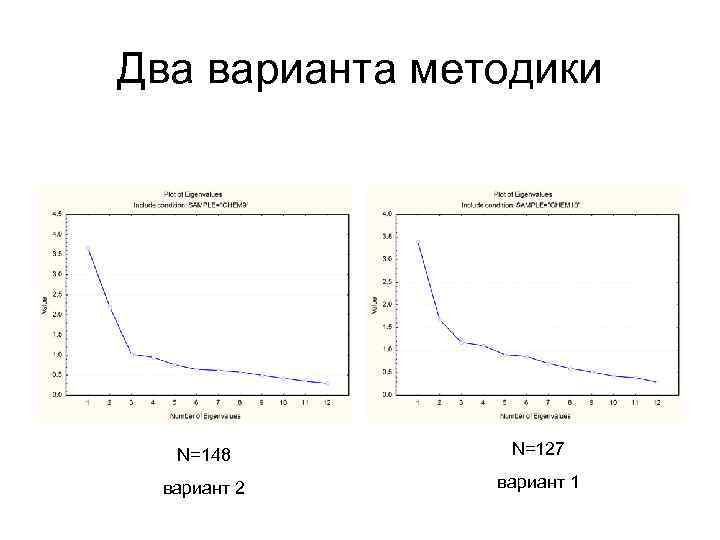Два варианта методики N=148 N=127 вариант 2 вариант 1
Эксплораторный ФА: шаг 3 • Вращение выделенных факторов: – ортогональное (корреляции факторов равны нулю); – косоугольное (факторы могут коррелировать).
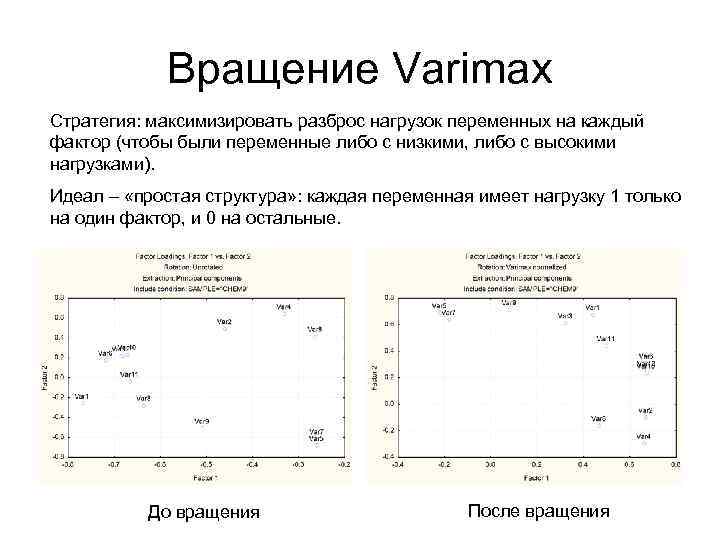Вращение Varimax Стратегия: максимизировать разброс нагрузок переменных на каждый фактор (чтобы были переменные либо с низкими, либо с высокими нагрузками). Идеал – «простая структура» : каждая переменная имеет нагрузку 1 только на один фактор, и 0 на остальные. До вращения После вращения
Анализ надёжности • Задача: оценить долю общей дисперсии набора переменных (можно ли из них сформировать шкалу? ) • Классическая тестовая теория предлагает нам альфа-коэффициент Кронбаха.
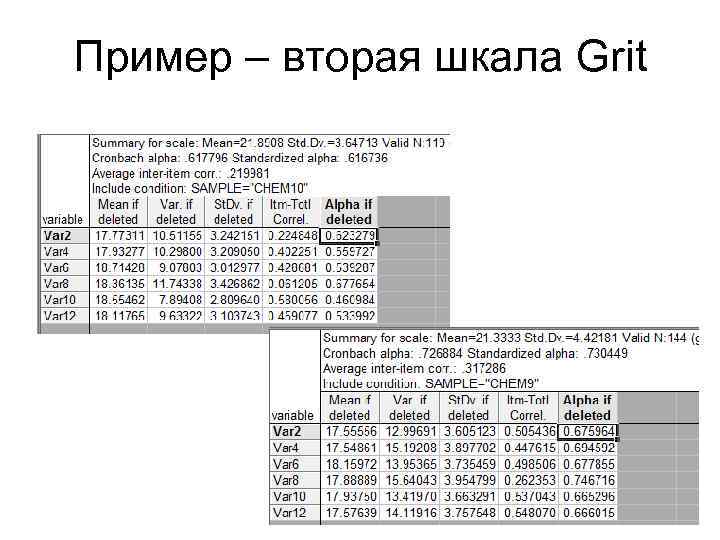Пример – вторая шкала Grit
Анализ надёжности • Ограничения модели. Предполагается, что: – ошибки переменных равны 0, – все нагрузки переменных на латентный фактор равны 1. • В реальности так не бывает если бы мы учли это и взвесили вопросы, мы получили бы более надёжную шкалу.
Конфирматорный факторный анализ • Задача: проверка гипотезы о соответствии наблюдаемых взаимосвязей набора переменных некоторой теоретически предполагаемой картине. • Проблема: одной и той же системе переменных могут быть адекватны разные варианты латентной структуры.
Конфирматорный ФА • Типичные задачи в психологии: – проверка гипотезы о структуре опросника; – проверка гипотезы о латентной структуре нескольких опросников, измеряющих одни и те же конструкты; – проверка гипотез о различной степени эквивалентности двух версий опросника (на разных языках)… – …либо одного и того же опросника на разных выборках (например, М и Ж).
Конфирматорный ФА • Допущения: – нормальное распределение (многомерная нормальность), хотя есть и непараметрические поправки для статистик; – как минимум 2 индикатора на латентный фактор; – объём выборки: чем больше, чем лучше; как минимум 5 наблюдений на параметр, а число параметров как минимум в 2 раза больше числа независимых переменных.
Конфирматорный ФА • На входе: данные по переменным + предполагаемая система их связей, заданная графически или уравнениями. • На выходе: показатели соответствия теоретической модели исходным данным.
Шкала субъективного счастья (Lyubomirsky & Lepper, 1999; перевод Д. А. Леонтьева и Е. Н. Осина)
Шкала удовлетворенности жизнью (Diener, Emmons, Larsen, Griffin, 1984; пер. Д. А. Леонтьева)
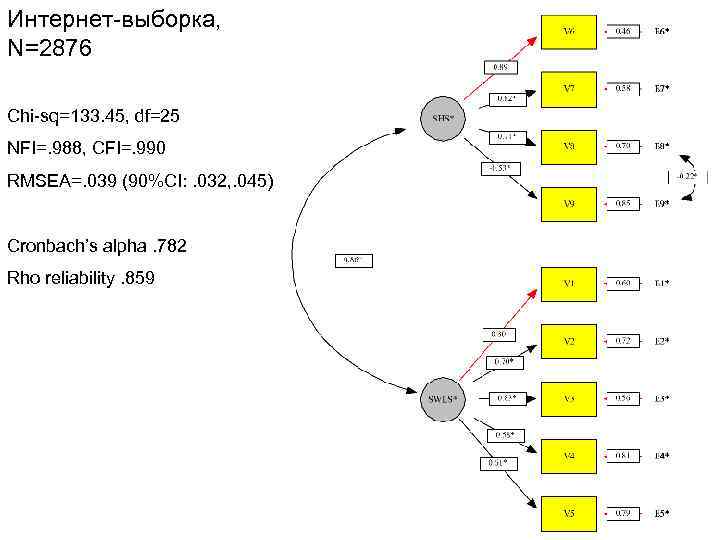Интернет-выборка, N=2876 Chi-sq=133. 45, df=25 NFI=. 988, CFI=. 990 RMSEA=. 039 (90%CI: . 032, . 045) Cronbach’s alpha. 782 Rho reliability. 859
Структурное моделирование • То же самое, что модель КФА, только латентные переменные предсказывают друга (и мы имеем для них ошибки – disturbance). • Лучше всего сначала применить к данным простейшую модель КФА (measurement model), и, только если она хорошо соответствует данным, вводить взаимосвязи.
Кластерный анализ • Задача – классификация набора переменных или набора наблюдений по нескольким переменным. • В психологии: выявить сложную структуру опросника, либо выявить типы испытуемых по набору параметров. • Исходные данные: измерены по любой шкале (но одинаковой) но надо правильно выбрать метрику.
Кластерный анализ • Иерархический КА – рассчитывает матрицу расстояний от каждого объекта (переменной или наблюдения) до каждого на основе метрики: • простое расстояние (Евклидово), сити-блок, процент совпадений, корреляция Пирсона и пр. – начинает объединять объекты по правилу (алгоритму): • метод ближайшего соседа, метод дальнего соседа, медианные, метод Уорда.
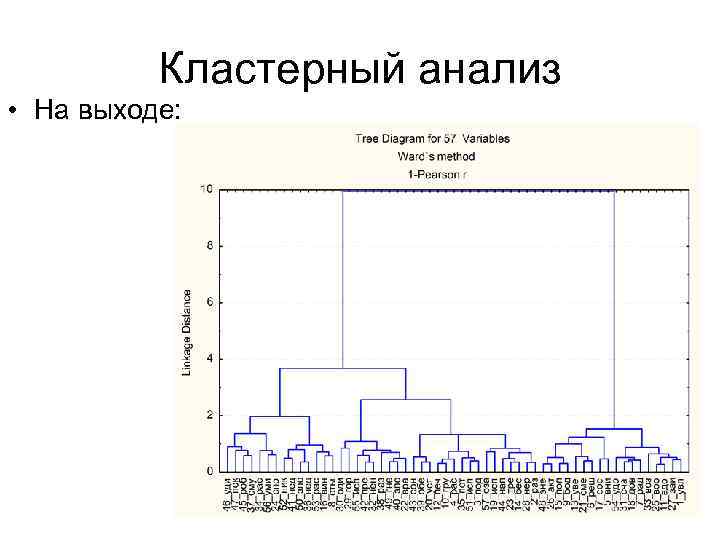Кластерный анализ • На выходе:
Многомерное шкалирование • На входе – матрица сходств или матрица различий ряда объектов. • Задача: выявление минимального количества измерений, позволяющих воспроизвести модель. • В психологии: выявление латентных измерений. Но чаще используется факторный анализ, т. к. он проще.
Многоуровневые методы • Если данные иерархически структурированы (школьники в нескольких классах, люди в нескольких странах), наблюдения не являются попарно независимыми. • В этом случае необходимо отделить общую дисперсию групп от дисперсии индивидов. • Методы: иерархическое линейное моделирование (HLM), ANOVA, структурное моделирование.
Шаги выбора метода • Определение набора исходных переменных и их места в анализе (есть ли независимые и зависимые). • Определение шкалы, по которой они измерены и характера распределения (допустимы ли параметрические методы). • Выбор оптимального метода из допустимых.
Литература • Наследов А. Д. Математические методы психологического исследования: анализ и интерпретация данных. СПб: Речь, 2004. • Tabachnik B. G. , Fidell L. S. Using Multivariate Statistics. Pearson: 2007.