Материалы обзорной лекции к экзамену по математике 1

Материалы обзорной лекции к экзамену по математике 1 курс 2 семестр сокращенные программы обучения

6 вопрос ФОРМУЛЫ ТЕЙЛОРА И МАКЛОРЕНА Функция y = f(x) (n+1) раз дифференцируема в окрестности точки x 0. Формула Тейлора - остаточный член в форме Лагранжа Формула Маклорена (х0 = 0) Пример. Формула Маклорена при n = 3

6 вопрос Разложение элементарных функций по формуле Маклорена Пример: Разложить функцию y = e-2 x, взяв 4 члена разложения и остаточный член

РАЗДЕЛ 1

1. Первообразная и неопределенный интеграл Первообразной F(x) для функции f(x) на промежутке [a, b] называют функцию, производная которой равна f(x). Теорема. Пусть функция F(x) – первообразная f(x), Ф(x) – другая первообразная f(x). Тогда F(x) = Ф(x) + С Неопределённым интегралом от функции f(x) на [a, b] называется множество всех первообразных F(x) функции f(x) на этом интервале. Обозначается: Если F(x) – одна из первообразных f(x) на [a, b], то

2 вопрос 1. 2. 3. 4. 5. 6. 7. Свойства неопределенного интеграла

ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ Таблица интегралов

3 вопрос Замена переменных в неопределенном интеграле Пусть х = φ(t) - непрерывно дифференцируемая и обратимая функция, на множестве значений которой определена функция у = f(x). Тогда Пример 1: Вычислить неопределенный интеграл Пример 2: Вычислить неопределенный интеграл

4 вопрос Интегрирование по частям в неопределенном интеграле Пример 3: Вычислить неопределенный интеграл

5 вопрос Интегрирование выражений, содержащих квадратный трехчлен 1. Выделяется полный квадрат в квадратном трехчлене: 2. Заменой x + α = t исходный интеграл сводится к табличным интегралам. Пример: Найти неопределенный интеграл 1. Выделим сначала полный квадрат из квадратного трехчлена: 2. Проведем замену переменных, положив x – 1 = t:

6 вопрос Интегрирование рациональных дробей Назовем простейшими сомножителями выражения вида где а вещественное, k, l натуральные числа, а квадратный трехчлен x 2 + px + q не имеет действительных корней. Основная теорема алгебры: Любой многочлен степени n Pn(x) можно разложить в произведение простейших сомножителей: (*) где А 0 число; k 1 + … + ks + 2 l 1 + …+ 2 lr = n. Будем называть простейшими рациональными дробями дроби вида где k, l натуральные числа, а (x 2 + px + q)l – простейший сомножитель.

Дробь называется правильной, если m < n. Если m ≥ n, дробь называется неправильной. (Здесь m и n – степени многочленов, стоящих в числителе и в знаменателе соответственно. ) Каждую неправильную дробь можно представить в виде суммы многочлена и правильной дроби: Теорема. Любая правильная рациональная дробь , где m < n, а Pn(x) – многочлен, определенный равенством (*), может быть представлена в виде суммы простейших рациональных дробей.

Разложение правильной дроби на простейшие строится в два этапа: 1. Каждый простейший множитель вида (x – а)kj порождает следующую сумму из kj слагаемых: 2. Каждый сомножитель вида (x 2 + px + q)li порождает следующую сумму из li слагаемых: В результате получим следующее разложение правильной дроби на простейшие:

Пример: Найти интеграл , разложив подынтегральное выражение на простейшие дроби. 1. Разложим знаменатель на простейшие сомножители: 2. Разложение имеет вид: 3. Приводим к общему знаменателю: 4. Две дроби, имеющие одинаковые знаменатели, равны, значит, равны их числители, то есть:

5. Два многочлена тождественно равны тогда, когда у них совпадают коэффициенты при одинаковых степенях х, следовательно, можно записать следующую систему уравнений: 6. Решая получившуюся систему, находим: 7. Получаем разложение на простейшие дроби: . 8. Вычисляем интеграл:

7 вопрос Интегрирование некоторых иррациональных алгебраических выражений Пусть R(x, у, …, z) – рациональное выражение. Тогда интеграл находится заменой переменных x = tr, где, за r, как правило, берется наименьшее общее кратное чисел n 1, …, nk, т. е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались: Аналогичным образом вычисляется интеграл

Пример: Вычислить неопределенный интеграл Сделаем следующую замену переменных:

8 вопрос Интегрирование тригонометрических выражений 1. Интегрирование выражений вида а) Среди чисел m, n есть хотя бы одно нечетное. Тогда за t принимается функция, стоящая в основании другой степени б) оба числа m, n четные неотрицательные. Положим m = 2 p, n = 2 q и применим формулы Тогда

2. Пусть R(x, y)- рациональное выражение. Тогда интеграл сводится к интегралу от рациональной функции с помощью универсальной тригонометрической подстановки: Пример: Найти неопределенный интеграл Сделаем универсальную тригонометрическую подстановку:

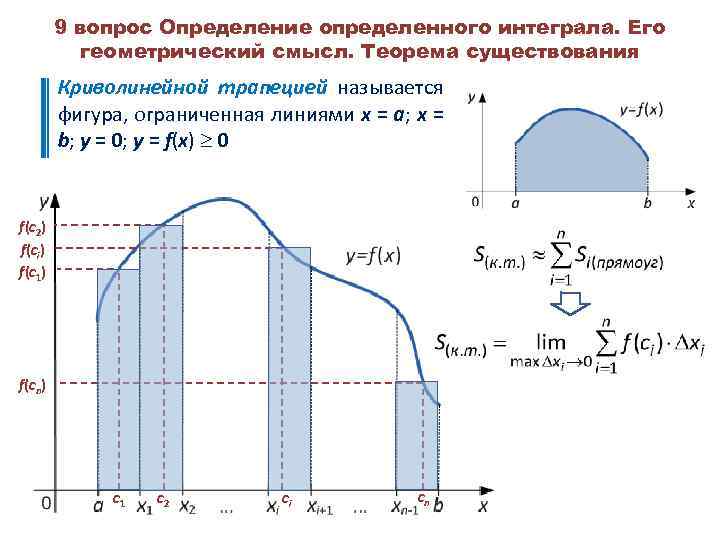
9 вопрос Определение определенного интеграла. Его геометрический смысл. Теорема существования Криволинейной трапецией называется фигура, ограниченная линиями x = a; x = b; y = 0; y = f(x) 0 f(с2) f(сi) f(с1) f(сn) с1 с2 сi сn

. Пусть функция y = f(x) определена на отрезке [a, b]. Разобьем отрезок [a, b] на n частей точками x 0, x 1, x 2, …, xn. Обозначим через xi = xi – xi-1. В каждом из отрезков возьмем точку сi [xi -1, xi] и вычислим в ней значение функции f(сi). Составим сумму: которую в дальнейшем будем называть интегральной суммой. Если существует предел интегральных сумм, при max│ xi │ 0, который не зависит ни от способов разбиения отрезка [a, b] на части, ни от способов выбора точек сi, то он называется определенным интегралом от функции f(x) по промежутку [a, b] Теорема (о существовании определенного интеграла) Если функция y = f(x) непрерывна на отрезке [a, b], то существует определенный интеграл

10 вопрос Свойства определенного интеграла Пусть функции f(x) и g(x)-непрерывны на [a, b] 1. 2. 3. 5. 4. 6. 7. 8. 9.

11 вопрос Интеграл с переменным верхним пределом и его производная Интегралом с переменным верхним пределом называется интеграл Теорема Если функция y=f(x) непрерывна, то Интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции У каждой непрерывной функции существует первообразная ! У каждой непрерывной функции существует неопределенный интеграл

12 вопрос Формула Ньютона-Лейбница , где F(x)-одна из первообразных f(x) Примеры: Вычислить определенные интегралы 1. 2.

13 вопрос Интегрирование по частям: Пример: Вычислить определенный интеграл Интегрирование с заменой переменной: Пример: Вычислить определенный интеграл ! При замене переменной в определённом интеграле нет необходимости возвращаться к старой переменной

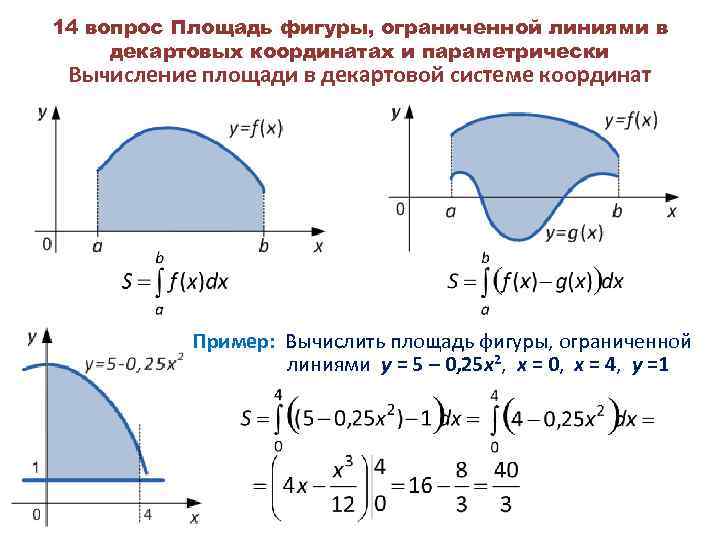
14 вопрос Площадь фигуры, ограниченной линиями в декартовых координатах и параметрически Вычисление площади в декартовой системе координат Пример: Вычислить площадь фигуры, ограниченной линиями y = 5 – 0, 25 х2, x = 0, x = 4, y =1

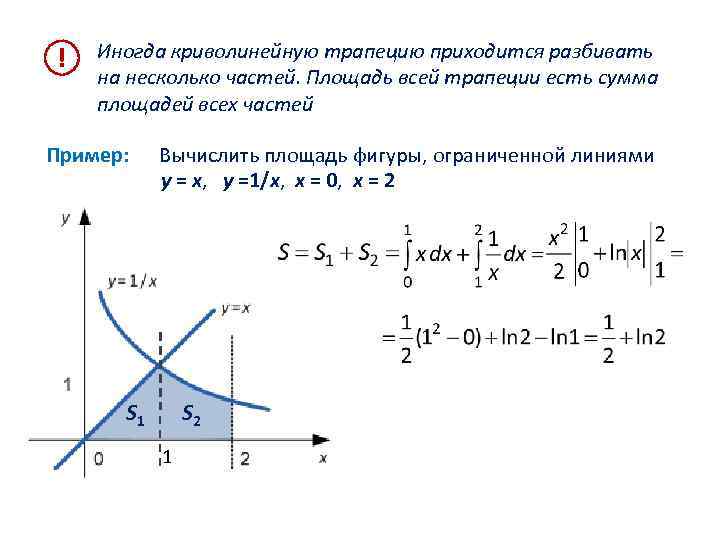
! Иногда криволинейную трапецию приходится разбивать на несколько частей. Площадь всей трапеции есть сумма площадей всех частей Пример: Вычислить площадь фигуры, ограниченной линиями y = х, y =1/х, x = 0, x = 2 S 1 S 2 1

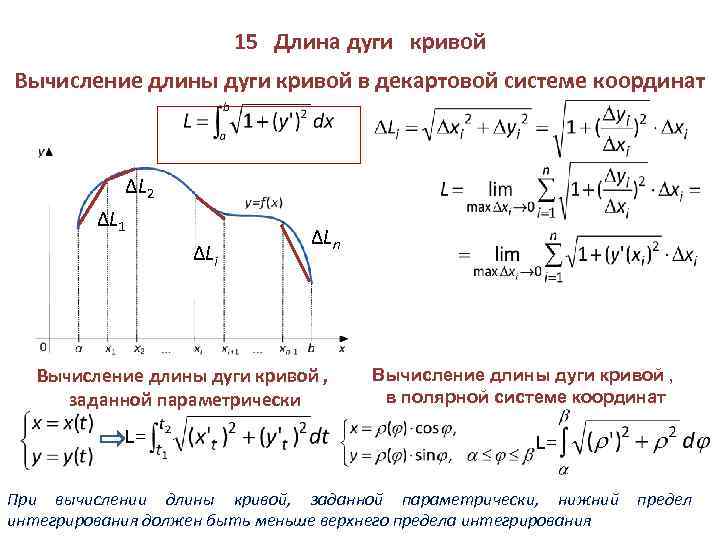
15 Длина дуги кривой Вычисление длины дуги кривой в декартовой системе координат ∆L 2 ∆L 1 ∆Li ∆Ln Вычисление длины дуги кривой , заданной параметрически L= Вычисление длины дуги кривой , в полярной системе координат L= При вычислении длины кривой, заданной параметрически, нижний интегрирования должен быть меньше верхнего предела интегрирования предел

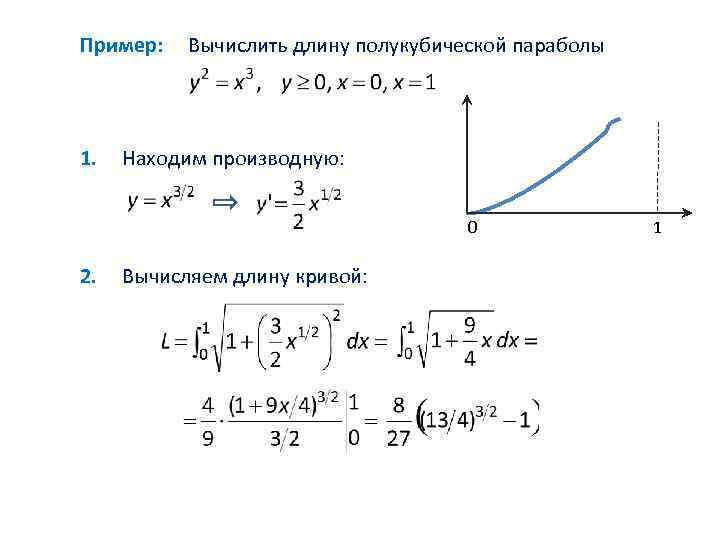
Пример: 1. Вычислить длину полукубической параболы Находим производную: 0 2. Вычисляем длину кривой: 1

16 вопрос Объем тела вращения Если криволинейная трапеция ограничена линиями x = a; x = b; y = 0; y = f(x), где f(x) 0 , и вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX S(x) Аналогично, для криволинейной трапеции, вращаемой вокруг оси OY и ограниченной линиями y = с; у = d; x = 0; x = φ(y), имеем:

30 вопрос Пример: Вычислить объем тела вращения, ограниченного линиями x = 0; x = 1; y = 0; y = e x y 0 1 x

31 вопрос НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ Несобственные интегралы первого рода (по бесконечному промежутку) Пусть функция f(x) непрерывна на промежутке [a; +∞). Если существует предел , то этот предел называется несобственным интегралом от функции f(x) по бесконечному промежутку [a; +∞) и обозначается Если указанный предел существует и конечен, то интеграл называется сходящимся. В противном случае (если предел бесконечен или не существует) говорят, что интеграл расходится

Аналогично вводится понятие несобственного интеграла по промежутку (–∞; a]: Несобственный интеграл определяется как сумма несобственных интегралов: ! Данное определение не зависит от выбора точки а Интеграл называется сходящимся, если сходящимися являются оба интеграла он называется расходящимся в противном случае

18 вопрос Несобственные интегралы второго рода (от неограниченных функций) Пусть функция f(x) непрерывна на [a; b] за исключением точки с є [a; b], в которой она терпит разрыв второго рода. Рассмотрим три случая: 1. с = а Возьмем произвольное положительное малое (чтобы выполнялось неравенство a+ε<b) ε и положим Если указанный предел существует, то называется несобственным интегралом второго рода по промежутку [a; b].

2. с = b 3. с є (a; b) В данном случае несобственный интеграл сходится, если сходятся слагаемые, определяющие этот интеграл Пример.

Примеры. Вычислить несобственный интеграл или доказать его расходимость 1. 2. - интеграл расходится 3. Поскольку данный предел не существует, то интеграл расходится

РАЗДЕЛ № 2

19 (1 ч) Функции двух переменных Пусть задано множество упорядоченных пар чисел (х, у), принадлежащее некоторой плоской области D. Правило (закон), который ставит в соответствие каждому набору (х, у) Є D единственное значение z Є R, называется функцией двух переменных z = f (х, у), действующей из D в R. При этом х и у называются независимыми переменными, а z – зависимой переменной. z Графиком функции двух переменных z = f (х, у) называется множество точек (х, у, f (х, у)). х 0 Множество D = D(f) называется областью определения функции; множество значений, принимаемых z в области определения называется областью значений функции, обозначается E или E(f) у

Функция z = f(x, y) называется непрерывной в точке M 0(x 0, y 0), если то есть если предел в точке M 0(x 0, y 0) совпадает со значением функции в этой точке. Если функция непрерывна в каждой точке некоторой области, то она непрерывна на всей этой области. 20 вопрос Предел и непрерывность функции 2 -х переменных.

21 вопрос Частные производные 1 -го порядка и их геометрический смысл Если существует предел при x 0 отношения приращения функции z = f (х, у) к приращению аргумента x, то он называется частной производной функции z по переменной x. Если существует предел при y 0 отношения приращения функции z = f (х, у) к приращению аргумента y, то он называется частной производной функции z по переменной y. ! При вычислении частных производных все переменные, кроме одной (той, по которой берется производная) считаются константами.

Пример. Вычислить частные производные следующей функции двух переменных: 1. Находим частную производную по х (y = const): 2. Находим частную производную по y (x = const):

22 Частный дифференциал функции 2 -х переменных Частным дифференциалом функции z = f(x, y) по переменной x называется главная часть частного приращения функции по переменной x, линейная относительно x. – частный дифференциал по переменной x Аналогично можно ввести понятие частного дифференциала функции по переменной y: 23 Полный дифференциал функции 2 -х переменных Полный дифференциал функции равен сумме его частных дифференциалов: Пример. Найти полный дифференциал функции:

24. Частные производные второго порядка Частные производные от частных производных называются частными производными второго порядка. Пример. Найти частные производные второго порядка функции: Теорема. Если функция z = f(x, y) непрерывна вместе со своими частными производным до второго порядка включительно, то смешанные производные второго порядка равны между собой:

25. Производная сложной функции.

26 вопрос Производная неявной функции Функция z = f(x, y) называется неявной, если она задается уравнением F(x, y, z)=0, неразрешимым относительно z. ; ; Пример. Найти частные производные функции z = f(x, y), заданной уравнением: Найдем частные производные:

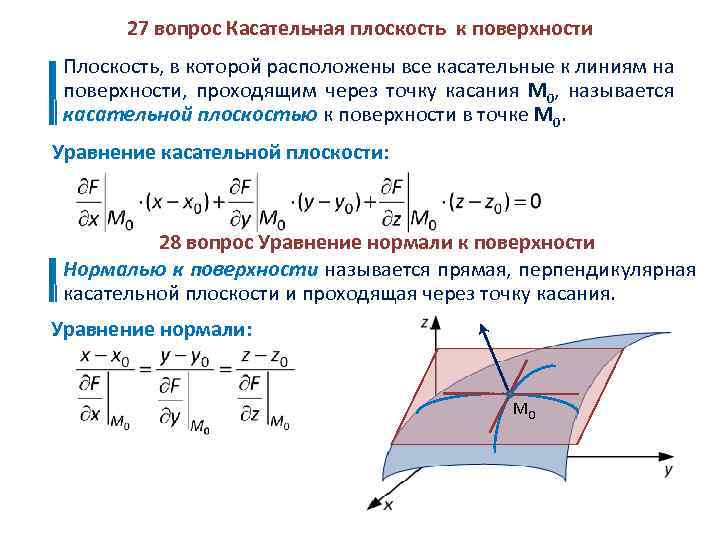
27 вопрос Касательная плоскость к поверхности Плоскость, в которой расположены все касательные к линиям на поверхности, проходящим через точку касания M 0, называется касательной плоскостью к поверхности в точке M 0. Уравнение касательной плоскости: 28 вопрос Уравнение нормали к поверхности Нормалью к поверхности называется прямая, перпендикулярная касательной плоскости и проходящая через точку касания. Уравнение нормали: М 0

29 вопрос Экстремумы функции двух переменных Функция f(x, y) имеет строгий локальный максимум (минимум) в точке М 0(х0, у0), если неравенство имеет место во всех точках М(х, у) ≠ М 0 из некоторой достаточно малой окрестности точки М 0. Необходимое условие экстремума: Если функция f(x, y) дифференцируема в точке (х0, у0) и имеет экстремум в этой точке, то её дифференциал равен нулю: Точка (х0, у0) называется стационарной точкой функции, если

29(2) вопрос Пусть (х0, у0) – стационарная точка функции f(x, y). Обозначим: Достаточные условия экстремума: 1. Если АС – В 2 > 0 и А < 0, то (х0, у0) – точка максимума. 2. Если АС – В 2 > 0 и А > 0, то (х0, у0) – точка минимума. 3. Если АС – В 2 < 0, то (х0, у0) не является точкой экстремума. 4. Если АС – В 2 = 0, то (х0, у0) может как быть, так и не быть точкой экстремума, поэтому требуется дополнительное исследование.

Пример: Исследовать на экстремум функцию 1. Найдем частные производные заданной функции: 2. Найдем стационарные точки, приравняв частные производные нулю: Единственной стационарной точкой является точка М (0, 0). 3. Найдем частные производные второго порядка: Так как АС – В 2 = 2∙ 0 – 22 = -2 < 0, то точка М (0, 0) не является точкой экстремума.

30 вопрос Производная функции по направлению у β М 0 0 l - направляющие косинусы α х Дадим вдоль вектора l приращение l ( x, y): Перейдём к пределу при l → 0: Производной функции f(x, y) по направлению l в точке M 0 называют число

31. Градиентом функции f(x, y) в точке M 0 называют вектор, имеющий своими координатами значения частных производных функции в точке M 0: ! Градиент функции в точке M 0 показывает направление наискорейшего роста функции в этой точке. Линией уровня функции f(x, y) называют геометрическое место точек, в которых функция принимает одно и то же значение: ! Градиент функции в точке M 0 перпендикулярен линии уровня, проходящей через данную точку.

Связь между градиентом и производной по направлению: ! Если , то производная по направлению равна нулю. ! Если , , то производная по направлению принимает максимальное значение. Пример: Вычислить градиент функции, длину градиента и производную по направлению в точке М 0: 1. 2. 3.

РАЗДЕЛ № 3