Математика в программировании Или вид на ПО изнутри

Объект исследования – ПО – математические методы Цель исследования – выяснить, зачем нужна и

Математика и ПО В высшей математике много разных областей. И всегда программирование и математика

Математика и ПО Для программирования самой часто используемой областью математики является дискретная математика, которая

Математика и ПО Ещё не нужно забывать про теорию вероятности и математическую статистику. Чаще

Математика и ПО Ну и если программировать графику, то там без знания линейной алгебры

Рекурсия Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг

Рекурсия В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная

Нахождение факториала function fak(N: Integer): Integer; begin; if((N=0)OR(N=1)) then Result:=1 else Result:=N*fak(N-1); end;

Практическое применение На самом деле применений рекурсии в программировании гораздо больше, чем кажется. Потому

Численное интегрирование begin if (a = b) then begin result := 0; exit end;

Матрицы в компьютерной графике Если w == 1, тогда вектор (x,y,z,1) – позиция в

Преобразование матриц Умножение матрицы на вектор, получаем изменённый вектор:

Преобразование матриц In C++, with GLM: In GLSL : glm::mat4 myMatrix;// объявляем матрицу glm::vec4

Преобразование матриц Перенос вершины на 10 единиц по оси X:

Преобразование матриц Туже матрицу переноса на 10 по Х умножим на направление:

Выводы В своём исследовании я пытался выяснить, зачем нужна и где практическая значимость математических

Литература Интернет ресурсы Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений. -

Скачать презентацию Математика в программировании Или вид на ПО изнутри

presentation.ppt

Количество слайдов: 42

>Математика в программировании Или вид на ПО изнутри Разработал: Бабичев А.А. Математика в программировании Или вид на ПО изнутри Разработал: Бабичев А.А.

>Объект исследования – ПО – математические методы Цель исследования – выяснить, зачем нужна и Объект исследования – ПО – математические методы Цель исследования – выяснить, зачем нужна и где практическая значимость математических методов в программировании Задачи: -разобраться в практическом значении математических методов в программировании; -Создать наиболее оптимальное ПО, которое выполняет необходимые функции и имеет простой интерфейс для демонстрации непосредственно решения математических задач в программировании; -Показать жизненные примеры использования сложных математических расчётов и аналитического подхода к созданию и применению их в ПО.

>VS VS

>Математика и ПО В высшей математике много разных областей. И всегда программирование и математика Математика и ПО В высшей математике много разных областей. И всегда программирование и математика идут рука об руку, потому что логика программирования строгая и формализованная, на ней очень легко применять выведенные в математике правила и законы.

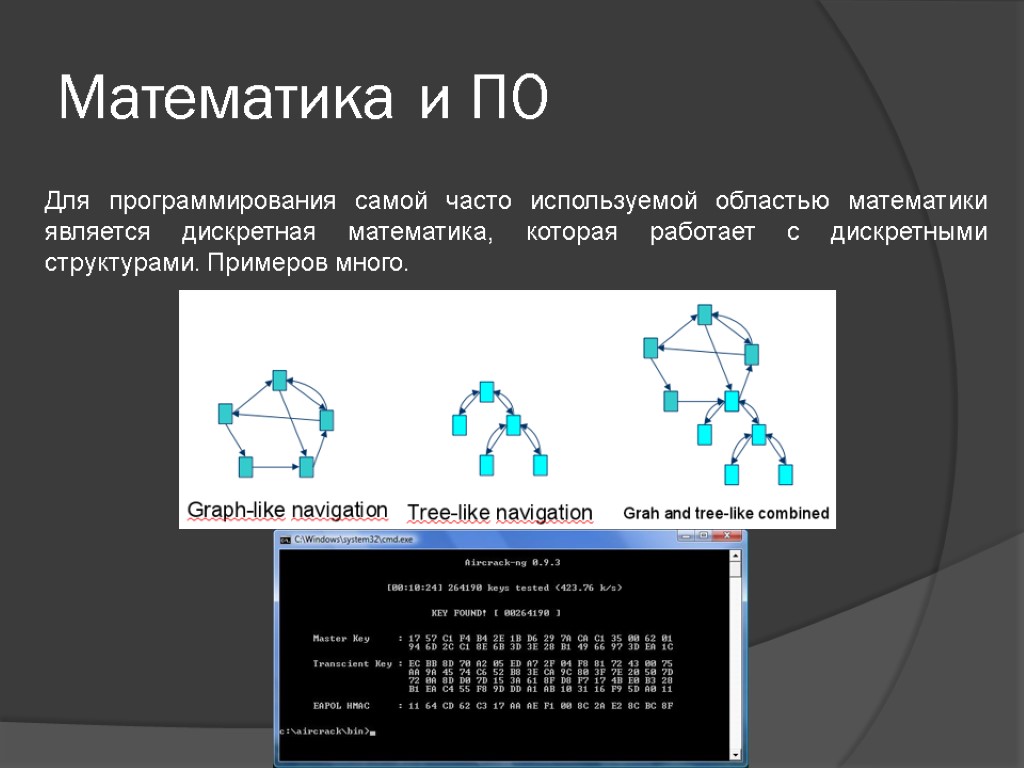
>Математика и ПО Для программирования самой часто используемой областью математики является дискретная математика, которая Математика и ПО Для программирования самой часто используемой областью математики является дискретная математика, которая работает с дискретными структурами. Примеров много.

>Математика и ПО Математика и ПО

>Математика и ПО Ещё не нужно забывать про теорию вероятности и математическую статистику. Чаще Математика и ПО Ещё не нужно забывать про теорию вероятности и математическую статистику. Чаще всего их законы используются в программировании игр и моделировании систем. Расчет случайных величин - важный прием программирования. Например, рассчитать, сколько урона нанесет юнит в игре. Или в какое время случится событие.

>Математика и ПО Ну и если программировать графику, то там без знания линейной алгебры Математика и ПО Ну и если программировать графику, то там без знания линейной алгебры и матриц не обойтись. Формул там действительно много. Кроме того, всегда может попасться задача из узкой области математики, и никогда заранее не знаешь, какие знания пригодятся для её решения.

>Рекурсия Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг Рекурсия Реку́рсия — процесс повторения элементов самоподобным образом. Например, если два зеркала установить друг напротив друга, то возникающие в них вложенные отражения суть одна из форм бесконечной рекурсии.

>Рекурсия В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная Рекурсия В математике и информатике рекурсия имеет отношение к методу определения функций: рекурсивно заданная функция в своём определении содержит себя, в частности, рекурсивной является функция, заданная рекурсивной формулой. function build_tree($cats,$parent_id){ if(is_array($cats) and isset($cats[$parent_id])){ $tree = '

'.$cat['name']; $tree .= build_tree($cats,$cat['id']); $tree .= '

'; } else return null; return $tree; }

>Нахождение факториала function fak(N: Integer): Integer; begin; if((N=0)OR(N=1)) then Result:=1 else Result:=N*fak(N-1); end; Нахождение факториала function fak(N: Integer): Integer; begin; if((N=0)OR(N=1)) then Result:=1 else Result:=N*fak(N-1); end;

>Практическое применение На самом деле применений рекурсии в программировании гораздо больше, чем кажется. Потому Практическое применение На самом деле применений рекурсии в программировании гораздо больше, чем кажется. Потому что рекурсия — это, пожалуй, единственный способ обхода любой древовидной структуры, когда заранее неизвестны ни ее размеры, ни глубина вложенности.

>Численное интегрирование begin if (a = b) then begin result := 0; exit end; Численное интегрирование begin if (a = b) then begin result := 0; exit end; if (a > b) then begin x := a; a := b; b := x; sign := -1 end else sign:=1; h := (b - a); s := y(a) + y(b); s2 := s; repeat s3 := s2; h := h/2; s1 := 0; x := a + h; repeat s1 := s1 + 2*y(x); x := x + 2*h; until (not(x < b)); s := s + s1; s2 := (s + s1)*h/3; x := abs(s3 - s2)/15 until (not(x > e)); result := s2*sign; end;

>Матрицы Матрицы

>Матрицы в компьютерной графике Если w == 1, тогда вектор (x,y,z,1) – позиция в Матрицы в компьютерной графике Если w == 1, тогда вектор (x,y,z,1) – позиция в пространстве Если w == 0, тогда вектор (x,y,z,0) - направление (X,Y,Z,w)

>Преобразование матриц Умножение матрицы на вектор, получаем изменённый вектор: Преобразование матриц Умножение матрицы на вектор, получаем изменённый вектор:

>Преобразование матриц In C++, with GLM: In GLSL : glm::mat4 myMatrix;// объявляем матрицу glm::vec4 Преобразование матриц In C++, with GLM: In GLSL : glm::mat4 myMatrix;// объявляем матрицу glm::vec4 myVector;// объявляем вектор // заполняем их как-нибудь glm::vec4 transformedVector = myMatrix * myVector; //умножаем матрицу //на вектор mat4 myMatrix;// объявляем матрицу vec4 myVector;// объявляем вектор // заполняем их как-нибудь vec4 transformedVector = myMatrix * myVector; //умножаем матрицу //на вектор

>Преобразование матриц Преобразование матриц

>Преобразование матриц Перенос вершины на 10 единиц по оси X: Преобразование матриц Перенос вершины на 10 единиц по оси X:

>Преобразование матриц Туже матрицу переноса на 10 по Х умножим на направление: Преобразование матриц Туже матрицу переноса на 10 по Х умножим на направление:

>Матрицы маштабирования Матрицы маштабирования

>Матрица модели Матрица модели

>Матрица камеры Матрица камеры

>Матрица проекции Матрица проекции

>Выводы В своём исследовании я пытался выяснить, зачем нужна и где практическая значимость математических Выводы В своём исследовании я пытался выяснить, зачем нужна и где практическая значимость математических методов в программировании. Я думаю что я достаточно убедил в необходимости знаний математических процессов для программиста, в зависимости от определённой деятельности. Я попытался вкратце наглядно продемонстрировать все те объекты которые я исследовал не используя «глобальных выкладок» с точки зрения математики и информатики

>Литература Интернет ресурсы Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений. - Литература Интернет ресурсы Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений. - Ростов н/Д: Феникс, 2010 Омельченко В.П., Кубатова Э.В. Математика: учебное пособие. - Ростов н/Д: Феникс, 2010 Шипачёв В.С. Начала высшей математики: Учебное пособие для вузов. – М.: Дрофа, 2010. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит. 2010 Лапчик М.П., М.И. Рагулина, Е.К. Хеннер Численные методы: Учебное пособие для студ вузов.- М. Издательский центр «Академия», 2010.