Математика в картинках Как запомнить циферки Сочиняем

Скачать презентацию Математика в картинках Как запомнить циферки Сочиняем

Математика в картинках_100 слайдов.ppt

Количество слайдов: 109

Математика в картинках

Как запомнить циферки? Сочиняем сказки! Нужно к каждой цифре придумать историю, в которой отразить «внешность» цифры. Например о том как лебединая верность и лебединые пары стали прообразом цифры « 2» 2

Как научиться писать красивые циферки? К каждой цифре придумать картинку, во что её можно превратить. И рисовать собственные шедевры. Математика – это область фантазии и воображения.

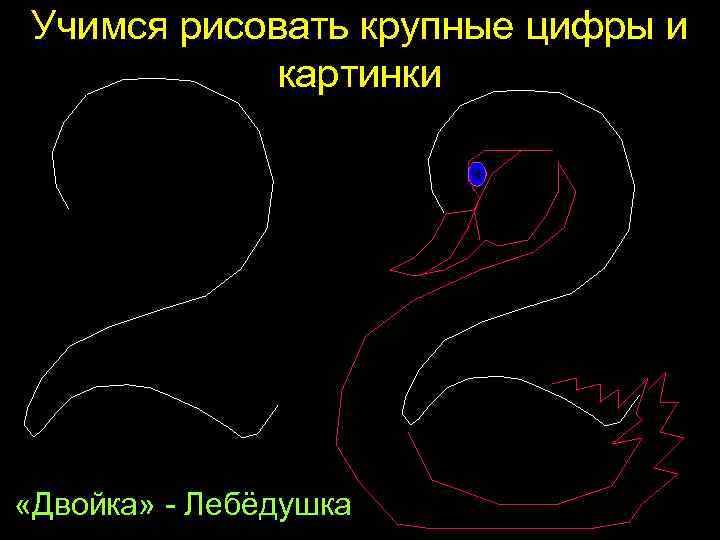Учимся рисовать крупные цифры и картинки «Двойка» - Лебёдушка

И красиво раскрашивать картинку «Девятка» - малютка

Можно рисовать циферку разными способами «Четвёрка» - Флажок, Оленёнок. Притча о том, как была придумана Четвёрка. Делая стульчик его всегда переворачивают, чтобы было удобно крепить ножки. Видя 4 ножки стула в процессе работы, люди решили что цифру 4 легко будет запомнить, если писать как Перевёрнутый стульчик. Похоже? А затем появились ещё несколько

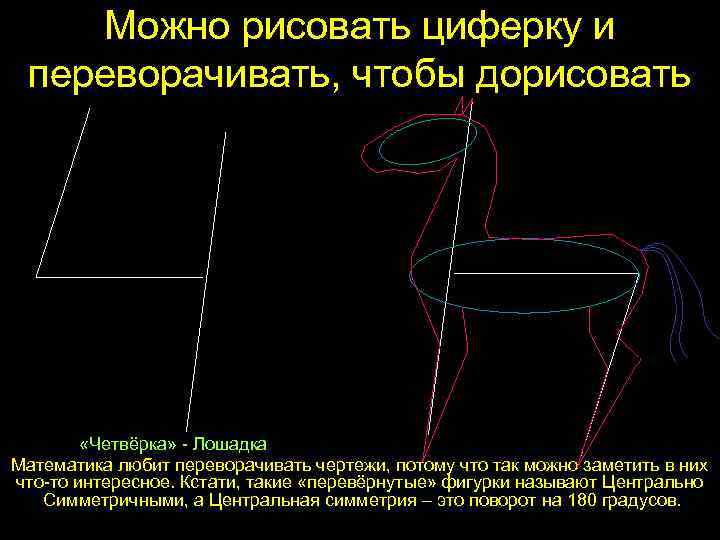Можно рисовать циферку и переворачивать, чтобы дорисовать «Четвёрка» - Лошадка Математика любит переворачивать чертежи, потому что так можно заметить в них что-то интересное. Кстати, такие «перевёрнутые» фигурки называют Центрально Симметричными, а Центральная симметрия – это поворот на 180 градусов.

Поиграем с Симметрией! Изобретаем качели! Как на даче делают качели «по-быстрому» ? К яблоне привязывают верёвку, на неё – сиденье… Яблоня ломается. Взрослые спорят, дети хнычут, яблоня болеет… Неужели из подручных средств нельзя придумать что-то лучше? «Палка + Бревно = Палка-качалка» Как сделать качели, не травмируя деревьев? По какому принципу устроены качели и карусели? Они должны быть хорошо сбалансированы. У качелей уравновешивают правую и левую часть относительно бревна (ось симметрии). А карусели надо уравновесить относительно Центра. Это заметили ещё древние математики и назвали это Осевой и Центральной Симметрией. С помощью картона, скрепок, скотча и других подручных средств сделай модель качели и карусели. Что с чем уравновешивается?

Как устроены карусели? Опыты с Центральной Симметрией 1. 2. 1. Вырежи из картона и проведи 2 вида испытаний: поставь на булавку и подвесь за нитку. Почему Центр симметрии является точкой опоры для равновесия? Почему картон нужен ровный с одинаковой плотностью? 2. Как из таких «деревянных» заготовок сделать качели и карусели? Как Центральная Симметрия помогает

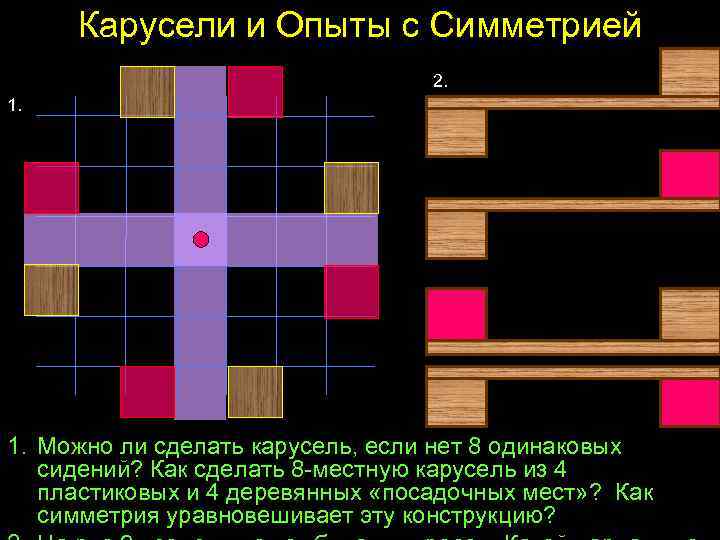Карусели и Опыты с Симметрией 2. 1. Можно ли сделать карусель, если нет 8 одинаковых сидений? Как сделать 8 -местную карусель из 4 пластиковых и 4 деревянных «посадочных мест» ? Как симметрия уравновешивает эту конструкцию?

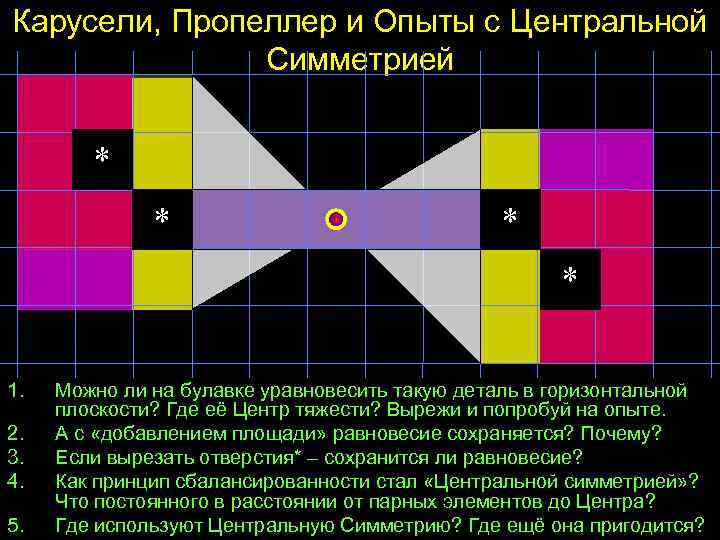Карусели, Пропеллер и Опыты с Центральной Симметрией * * 1. 2. 3. 4. 5. Можно ли на булавке уравновесить такую деталь в горизонтальной плоскости? Где её Центр тяжести? Вырежи и попробуй на опыте. А с «добавлением площади» равновесие сохраняется? Почему? Если вырезать отверстия* – сохранится ли равновесие? Как принцип сбалансированности стал «Центральной симметрией» ? Что постоянного в расстоянии от парных элементов до Центра? Где используют Центральную Симметрию? Где ещё она пригодится?

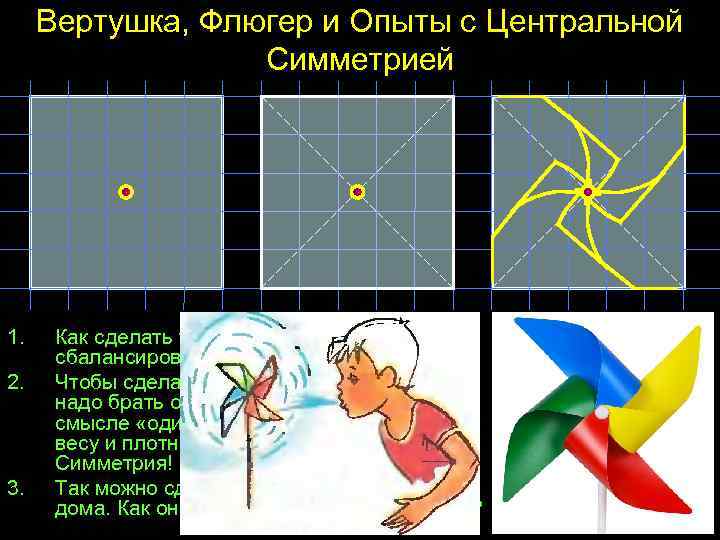Вертушка, Флюгер и Опыты с Центральной Симметрией 1. 2. 3. Как сделать такую «вертушку» ? Что надо сбалансировать вокруг центра? Чтобы сделать разноцветные лепестки – надо брать одинаковый материал. В каком смысле «одинаковый» ? Одинаковость по весу и плотности - это тоже Центральная Симметрия! Так можно сделать и флюгер на крышу дома. Как он будет показывать силу ветра?

Играем в Центральную Симметрию Центральная Симметрия на чертеже – это поворот фигур на 180 градусов вокруг Центра Симметрии (как если бы там была кнопка или гвоздик). Всё это легко проверить на Опытах и запомнить с помощью шуток. Про физический смысл Ц/Симметрии: Без баланса еле-еле Нас катали карусели. Взяли мы линейку в руки За работой не до скуки: Всё от Центра отмеряем, Всё от Центра размечаем, Симметричен стал баланс – И кружим который час! Про построение фигур в Ц/Симметрии: Через Центр неваляшку Повернули вверх тормашкой. Был сначала дом как дом – Отразился дом вверх дном.

Отражение в зеркале – это Осевая симметрия.

СИММЕТРИЯ – это здорово! Бывает так: согнёшь картинку – И совпадают половинки. То – Симметрия Осевая. Мы знаем. Есть у нас такая Что такое Симметрия?

Отражение в нескольких зеркалах – это самая удивительная симметрия. Картинка, Зеркала и Скотч - Изобретаем Калейдоскоп!

Отражение в нескольких зеркалах – это самая удивительная симметрия. Возьмите 2 зеркала и попробуйте поставить их под разными углами друг к другу: 30, 45, 60, 90, 120 градусов. Как меняется количество отражений? Что будет если зеркала поставить под прямым углом и придвинуть картинку к ним вплотную? Во сколько раз больше картинок стало? Математика - это не «цифры на бумаге» , это интересные законы жизни! Опыты с симметрией – это здорово!

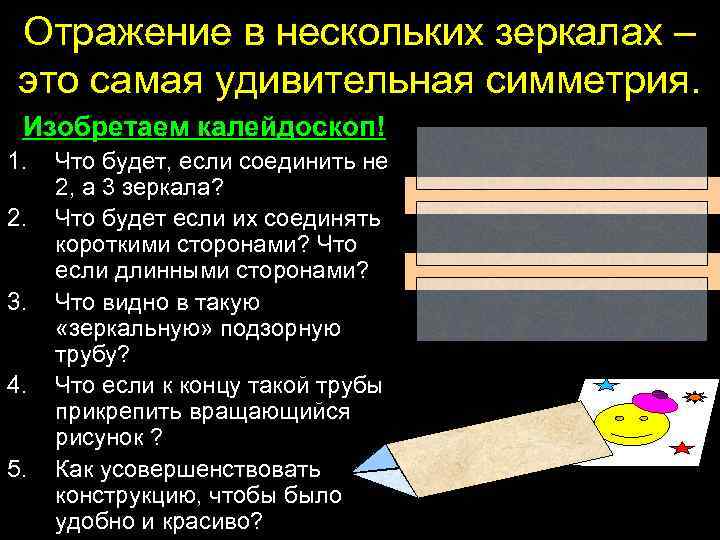Отражение в нескольких зеркалах – это самая удивительная симметрия. Изобретаем калейдоскоп! 1. 2. 3. 4. 5. Что будет, если соединить не 2, а 3 зеркала? Что будет если их соединять короткими сторонами? Что если длинными сторонами? Что видно в такую «зеркальную» подзорную трубу? Что если к концу такой трубы прикрепить вращающийся рисунок ? Как усовершенствовать конструкцию, чтобы было удобно и красиво?

Какие буквы можно отразить в вертикальном зеркале и они останутся правильными? А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я Ъ Ь Ы

Какие буквы можно разрезать по вертикали и отразить в зеркале, и они остались бы правильными? А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я Ъ Ь Ы

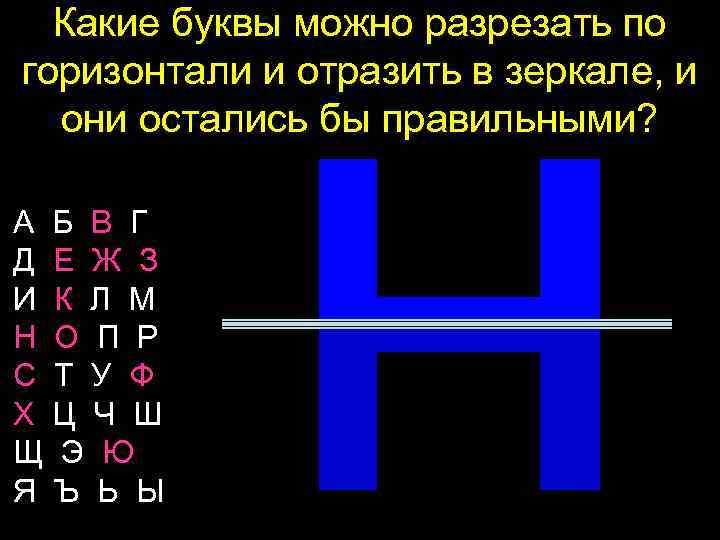Какие буквы можно разрезать по горизонтали и отразить в зеркале, и они остались бы правильными? А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я Ъ Ь Ы

Какую букву можно разрезать и по вертикали и по горизонтали? А отразив четвертинку в двух зеркалах вновь получить эту букву? А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я Ъ Ь Ы

Простые построения и задачки Грабельками нарисованы группы линий. Как это сделано? Как называются эти линии? Что такое «прямые» и «кривые» ? Где тут параллельные? Почему не говорят «параллельные кривые» ? Какая группа линий называется «со сдвигом» ? Что куда сдвинуто? Чем «сдвиг» похож на «сдвиг трафарета» ? Почему «Концентрическими» называют только круги? Что такое Центр Круга? Как можно нарисовать Концентрические круги? Какие фигуры можно придумать с этими линиями?

Простые построения и задачки Как Грабельками в 2 действия нарисовать много клеточек? Сколько синих прямых на рисунке? 12 прямых. Сколько клеток получилось? 25 клеток. Сколько всего параллельных прямых на рисунке? Горизонтальные параллельные: 6 синих и 2 белых. И Вертикальные параллельные: тоже 6 синих и 2 белых. Два множества по 8 штук в каждом. Сколько квадратов на рисунке справа? Что такое Квадрант и Квадрат?

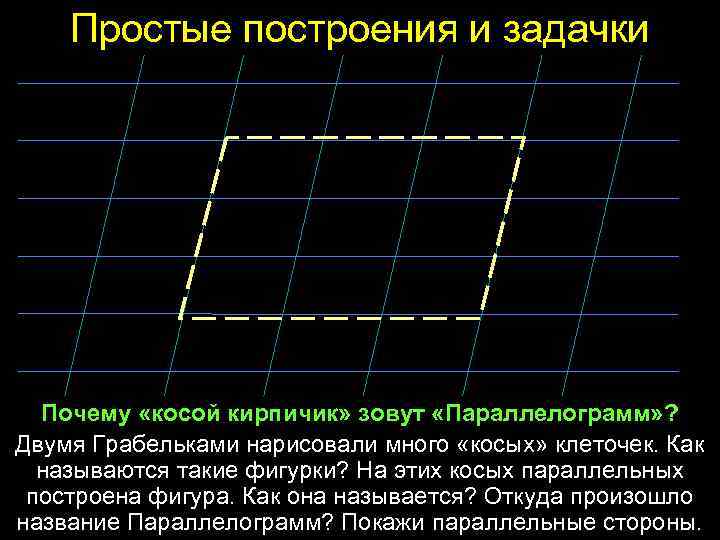Простые построения и задачки Почему «косой кирпичик» зовут «Параллелограмм» ? Двумя Грабельками нарисовали много «косых» клеточек. Как называются такие фигурки? На этих косых параллельных построена фигура. Как она называется? Откуда произошло название Параллелограмм? Покажи параллельные стороны.

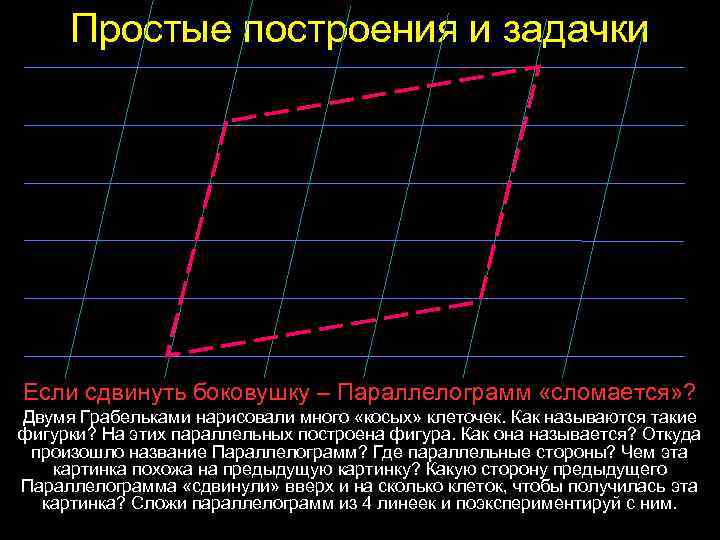Простые построения и задачки Если сдвинуть боковушку – Параллелограмм «сломается» ? Двумя Грабельками нарисовали много «косых» клеточек. Как называются такие фигурки? На этих параллельных построена фигура. Как она называется? Откуда произошло название Параллелограмм? Где параллельные стороны? Чем эта картинка похожа на предыдущую картинку? Какую сторону предыдущего Параллелограмма «сдвинули» вверх и на сколько клеток, чтобы получилась эта картинка? Сложи параллелограмм из 4 линеек и поэкспериментируй с ним.

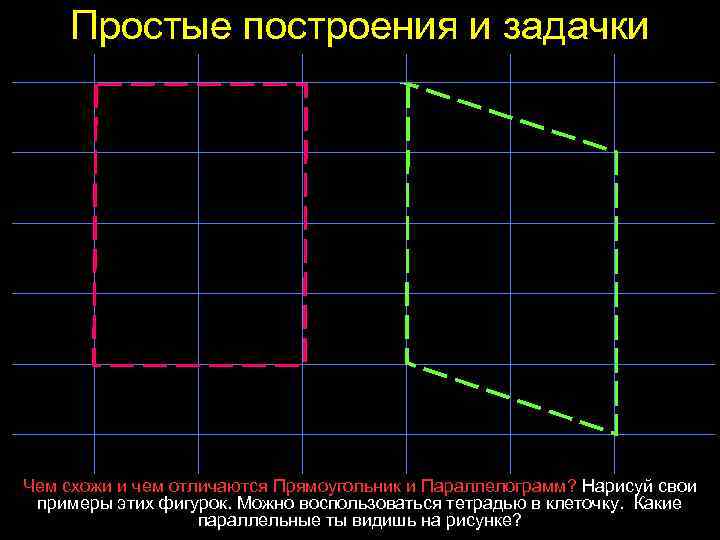Простые построения и задачки Чем схожи и чем отличаются Прямоугольник и Параллелограмм? Нарисуй свои примеры этих фигурок. Можно воспользоваться тетрадью в клеточку. Какие параллельные ты видишь на рисунке?

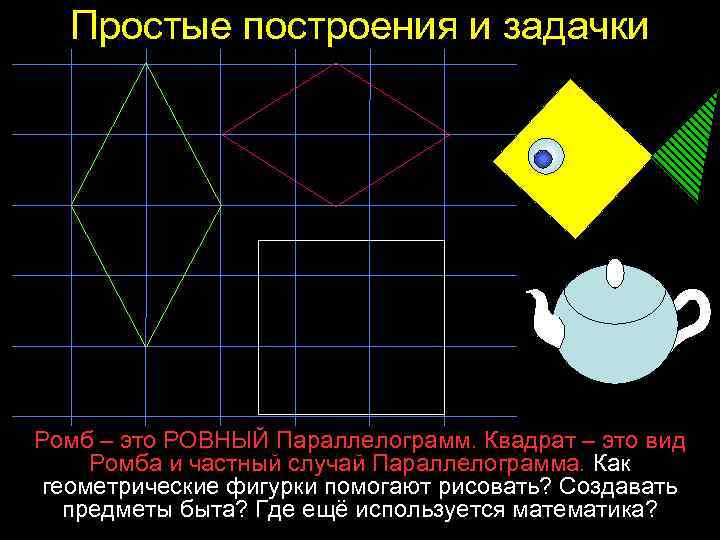Простые построения и задачки Ромб – это РОВНЫЙ Параллелограмм. Квадрат – это вид Ромба и частный случай Параллелограмма. Как геометрические фигурки помогают рисовать? Создавать предметы быта? Где ещё используется математика?

Параллельные прямые и Угол перечеркнули Грабельками. 4 параллельных на одинаковом расстоянии друг от друга. Сколько получилось Треугольников? Какие углы одинаковые? Чем похожи эти Треугольники?

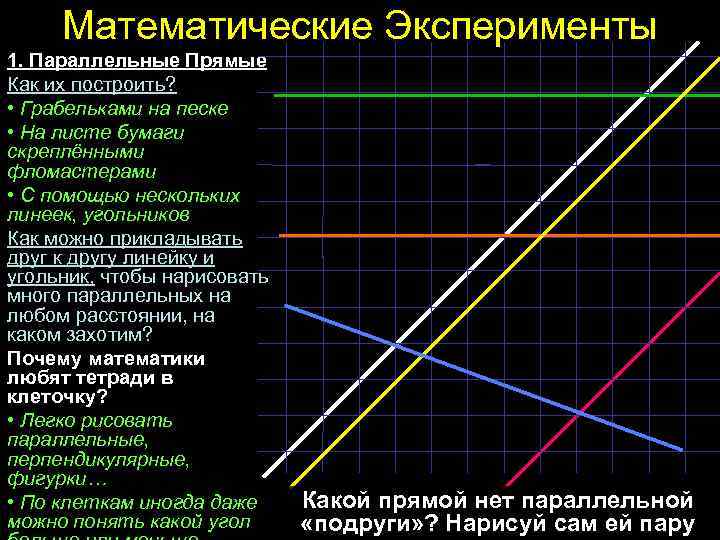Математические Эксперименты 1. Параллельные Прямые Как их построить? • Грабельками на песке • На листе бумаги скреплёнными фломастерами • С помощью нескольких линеек, угольников Как можно прикладывать друг к другу линейку и угольник, чтобы нарисовать много параллельных на любом расстоянии, на каком захотим? Почему математики любят тетради в клеточку? • Легко рисовать параллельные, перпендикулярные, фигурки… • По клеткам иногда даже можно понять какой угол Какой прямой нет параллельной «подруги» ? Нарисуй сам ей пару

Математические Эксперименты Почувствуй себя изобретателем! Параллельные Прямые Как ещё их можно построить? Как работают эти Как изобретали Рейсшину? приспособления? Как выглядит кухонная скалочка? Где у неё параллельные края? • Как катают скалочку? Видели параллельные следы на тесте? • Если прикрепить рамку из линеек можно рисовать параллельные? • Как придумали улучшить Рейсшину? Металл, пластик, резина; цифры, шкалы, трафареты, углы в градусах… • Разные «фасоны» у рейсшины – а смысл всегда одинаков – она сделана, чтобы ровно сдвигать линию

Математические Эксперименты 2. Круг и его «Родня» . Способы рисования? • Нитка и карандаш. Чем придержать центр? • Нитка, карандаш, кнопка. Приколоть центр! • А если 2 кнопки ? Длинный Круг = Эллипс. Линия движения планет. Родня Круга. • А если кнопки сдвигать ближе? Круглее! • А если сдвинуть до предела? Круг – это самый «ровный» эллипс, у Изобретаем Циркуль которого фокусы совпадают. Если вместе: узнаем всё о круге – то и об эллипсе Чтобы рисовать ровный КРУГ нам НАДО: легко поймём. Просто «растянем одну координату» . • Фиксировать Центр • Удерживать Радиус • Пишущий грифель или карандаш • Складной и Раскладной Циркуль – самый универсальный способ рисовать круг. Просто надо потренироваться Нарисуйте 10 кружочков. Закрасьте 5 из них. Чем отличается Круг и Окружность?

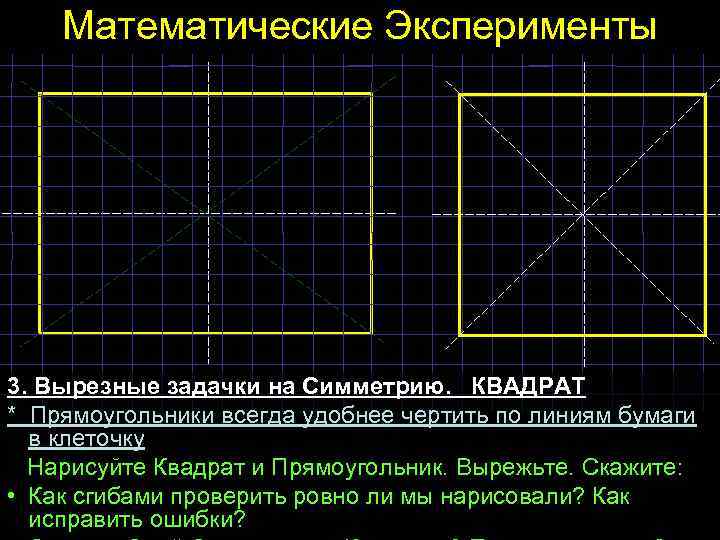Математические Эксперименты 3. Вырезные задачки на Симметрию. КВАДРАТ * Прямоугольники всегда удобнее чертить по линиям бумаги в клеточку Нарисуйте Квадрат и Прямоугольник. Вырежьте. Скажите: • Как сгибами проверить ровно ли мы нарисовали? Как исправить ошибки?

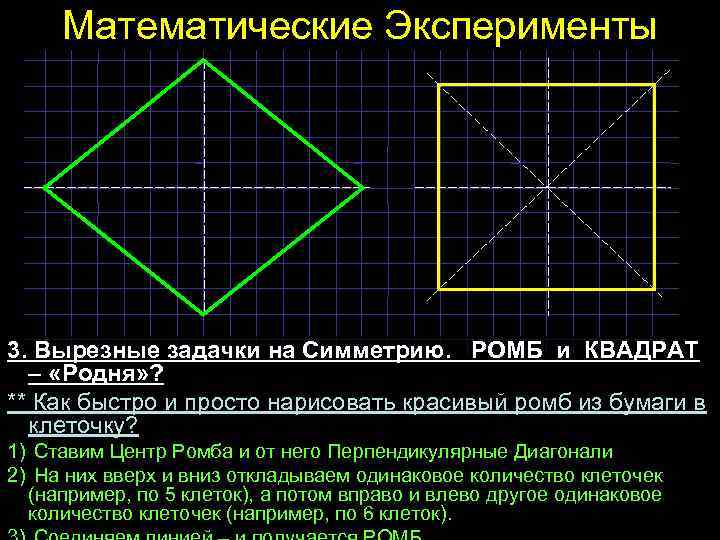Математические Эксперименты 3. Вырезные задачки на Симметрию. РОМБ и КВАДРАТ – «Родня» ? ** Как быстро и просто нарисовать красивый ромб из бумаги в клеточку? 1) Ставим Центр Ромба и от него Перпендикулярные Диагонали 2) На них вверх и вниз откладываем одинаковое количество клеточек (например, по 5 клеток), а потом вправо и влево другое одинаковое количество клеточек (например, по 6 клеток).

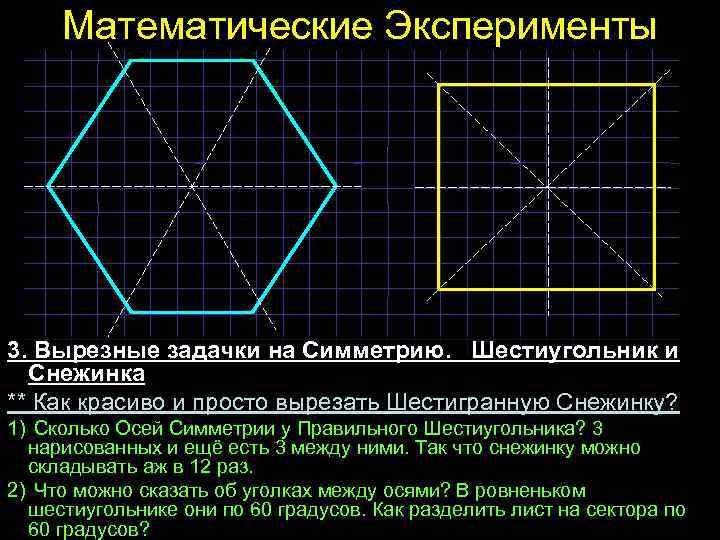Математические Эксперименты 3. Вырезные задачки на Симметрию. Шестиугольник и Снежинка ** Как красиво и просто вырезать Шестигранную Снежинку? 1) Сколько Осей Симметрии у Правильного Шестиугольника? 3 нарисованных и ещё есть 3 между ними. Так что снежинку можно складывать аж в 12 раз. 2) Что можно сказать об уголках между осями? В ровненьком шестиугольнике они по 60 градусов. Как разделить лист на сектора по 60 градусов?

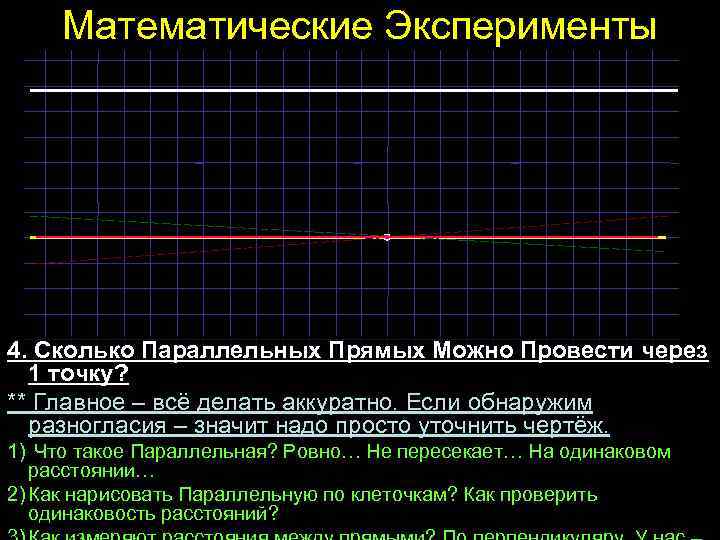Математические Эксперименты 4. Сколько Параллельных Прямых Можно Провести через 1 точку? ** Главное – всё делать аккуратно. Если обнаружим разногласия – значит надо просто уточнить чертёж. 1) Что такое Параллельная? Ровно… Не пересекает… На одинаковом расстоянии… 2) Как нарисовать Параллельную по клеточкам? Как проверить одинаковость расстояний?

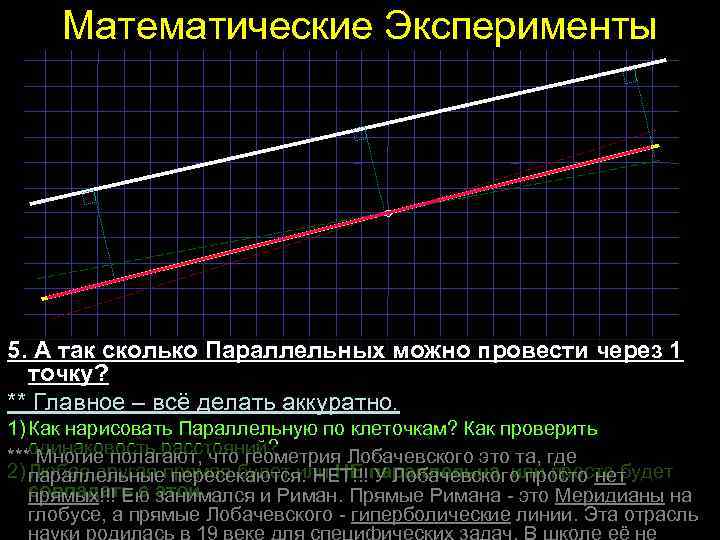Математические Эксперименты 5. А так сколько Параллельных можно провести через 1 точку? ** Главное – всё делать аккуратно. 1) Как нарисовать Параллельную по клеточкам? Как проверить одинаковость расстояний? *** Многие полагают, что геометрия Лобачевского это та, где 2) Любая другая прямая будет или НЕ параллельна, или просто будет параллельные пересекаются. НЕТ!!! У Лобачевского просто нет совпадать с этой. прямых!!! Ею занимался и Риман. Прямые Римана - это Меридианы на глобусе, а прямые Лобачевского - гиперболические линии. Эта отрасль науки родилась в 19 веке для специфических задач. В школе её не

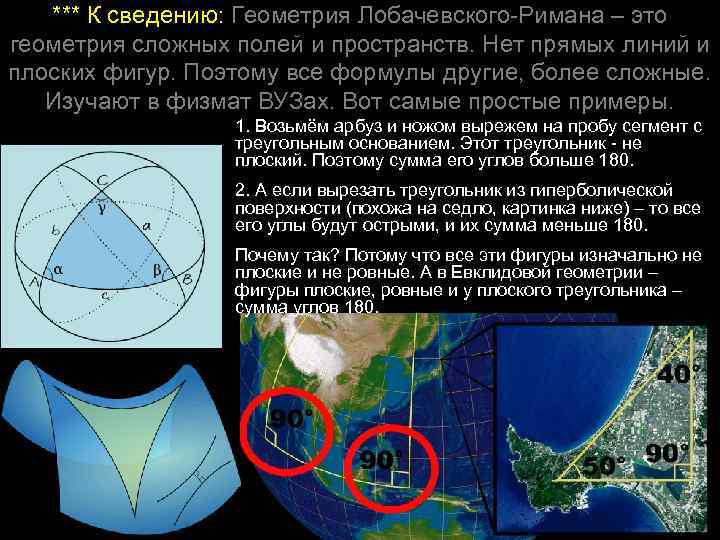*** К сведению: Геометрия Лобачевского-Римана – это геометрия сложных полей и пространств. Нет прямых линий и плоских фигур. Поэтому все формулы другие, более сложные. Изучают в физмат ВУЗах. Вот самые простые примеры. 1. Возьмём арбуз и ножом вырежем на пробу сегмент с треугольным основанием. Этот треугольник - не плоский. Поэтому сумма его углов больше 180. 2. А если вырезать треугольник из гиперболической поверхности (похожа на седло, картинка ниже) – то все его углы будут острыми, и их сумма меньше 180. Почему так? Потому что все эти фигуры изначально не плоские и не ровные. А в Евклидовой геометрии – фигуры плоские, ровные и у плоского треугольника – сумма углов 180.

Математические Эксперименты • 6. По какой линии пересекаются плоскости? Варианты: • Прямая Кривая • Дуга Сложная линия? . . Найдите вокруг себя примеры пересечения плоскостей (стены, пол со стеной, книга, тетрадка, 2 листка бумаги…) Какая линия соединяет плоскости? Оцените ровность плоскостей по степени ровности этой линии их пересечения? Особенно интересно с листками тетради. Ровные плоскости пересекаются по ровным прямым линиям. Можно согнуть лист – и линия сгиба поделит его на 2 плоскости.

Математические Эксперименты А Вы знаете, чем так интересны Медианы? Высота – понятно, по ней вычисляют площадь. Биссектриса – тоже ясно, часто используется как ось симметрии угла. А зачем нужна 7. Ищем Медиана? Что в ней Центр Тяжести Треугольника. Волшебство Медиан. особенного? Из плотной бумаги (картона) вырежьте несколько Треугольников. Прочертите на каждом Медианы, Биссектрисы и Высоты. Проведите эксперимент и проверьте вдоль каких линий расположится отвес в каждом случае. С какой точкой совпадает Центр Тяжести – с пересечением высот, медиан или биссектрис? Для удобства можно высоты рисовать одним цветом, биссектрисы другим цветом, медианы – третьим. Ход Эксперимента: 1) Из нити и грузика сделайте отвес и привяжите его к кнопке, на которую будете подвешивать Треугольник. 2) С помощью булавки или кнопки приколите Треугольник за один уголок так, чтобы он мог свободно раскачиваться. 3) Проверьте с чем совпадает нить отвеса. Можно сделать пометку.

Учись учиться - весело играя! Термины – это интересно! 1. 2. 3. В разных науках встречаются одинаковые термины. Когда это родственные понятия – то легко заметна аналогия и запоминать их легче, сравнив со словами - «друзьями» . Иногда аналогия не столь ясна на первый взгляд. Особенно, когда название сложилось исторически и слова-родоначальники претерпевали изменения, кочуя из одного языка в другой. Такие понятия проще сначала освоить там, где они встретились, а после само по себе придёт понимание их родственных связей и аналогий. Если уж какой-то термин Вам очень напоминает другое слово (схожи по звуковому рисунку) – постарайтесь узнать значения обоих слов и представить себе их на картинке, отметив для себя чем они отличаются. Простой пример «Гиена» и «Гигиена» , в треугольнике есть «Медиана» , а на глобусе Игра 1. Пары «Меридианы» . предложений: «Держите в порядке коврик и мышку» , «Мышку следует ежедневно кормить злаковыми культурами» ; «Одевайтесь со вкусом и будете всегда в тренде, «Линия тренда показывает куда стремится график» ; «Двойка сломалась! Будем пломбировать» , «Двоечкой бей – и

Учись учиться - весело играя! Термины – это интересно! Игра 2. Крылатые фразы и шутки: «Ноль без палочки» , «Мне большую половину!» , «И пошёл ровно по синусоиде» , «Планеты вокруг Солнца вращаются по концентрическим окружностям, каждая из которых – эллипс» . Игра 3. Буква заблудилась: «Из точки А в точку В проведён обрезок длиной 3 см» . «От рулона ткани осталось два маленьких отрезка» . Игра 4. Дорисуй картинки. Где здесь половинки, а где нет? Почему? Из каких фигурок составлен каждый рисунок на варежках и вазочках?

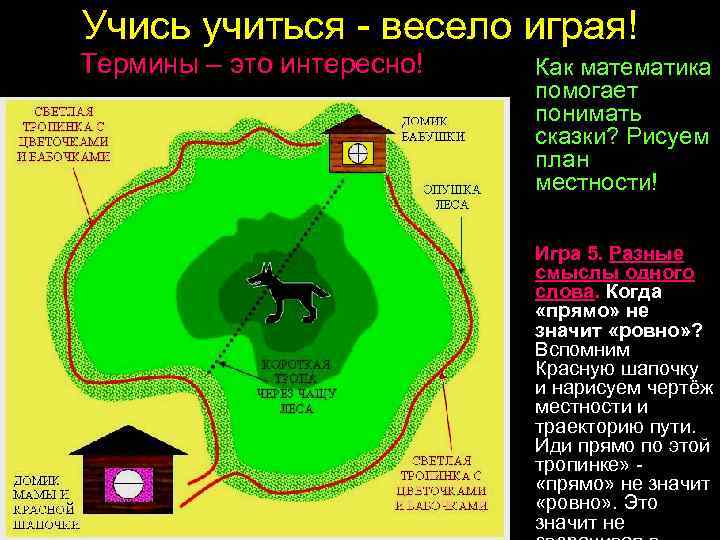Учись учиться - весело играя! Термины – это интересно! Как математика помогает понимать сказки? Рисуем план местности! Игра 5. Разные смыслы одного слова. Когда «прямо» не значит «ровно» ? Вспомним Красную шапочку и нарисуем чертёж местности и траекторию пути. Иди прямо по этой тропинке» - «прямо» не значит «ровно» . Это значит не

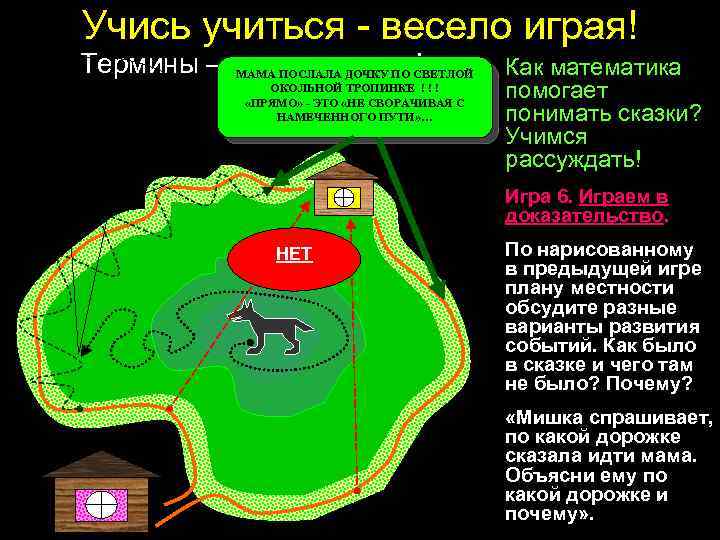Учись учиться - весело играя! Термины – это интересно! МАМА ПОСЛАЛА ДОЧКУ ПО СВЕТЛОЙ ВОЛК ПЛОХОЙ, ОН ВЫСЛЕЖИВАЛ, ЖДАЛ УДОБНОГО МОМЕНТА, КОГДА ОНА НЕЧАЯННО ЗАЙДЁТ В ЛЕСНУЮ ТЕНЬ… ОКОЛЬНОЙ ТРОПИНКЕ ! ! ! «ПРЯМО» - ЭТО «НЕ СВОРАЧИВАЯ С НАМЕЧЕННОГО ПУТИ» … Как математика помогает понимать сказки? Учимся рассуждать! Игра 6. Играем в доказательство. НЕТ По нарисованному в предыдущей игре плану местности обсудите разные варианты развития событий. Как было в сказке и чего там не было? Почему? «Мишка спрашивает, по какой дорожке сказала идти мама. Объясни ему по какой дорожке и почему» .

Учись учиться - весело играя! Игра 7. Софизмы. Математики шутят… Софизм – это нетождественные преобразования. Софизм ничего никогда не доказывает, но полезен как игра и упражнения. Укажите преобразования, нарушающие ОДЗ?

Учись учиться - весело играя! Софизмы. Математики шутят… Софизм – это нетождественные преобразования. Софизм ничего никогда не доказывает, но полезен как игра и упражнения. Укажите преобразования, нарушающие ОДЗ?

Учись учиться - весело играя! Софизмы. Математики шутят… Софизм – это нетождественные преобразования. Софизм ничего никогда не доказывает, но полезен как игра и упражнения. Софизм учит думать и критично подходить к своим и чужим Как доказать, что 2 х 2 = 6 ? рассуждениям. Отнимем от левой и правой части уравнения по 5. Получим: - 1 = 1 Укажите преобразования, нарушающие ОДЗ? Теперь возведём это в квадрат. Получим: 1 = 1 - верное равенство Значит 2 х 2 = 6 - верно?

Учись учиться - весело играя! Софизмы. Математики шутят… Софизм – это нетождественные преобразования. Софизм ничего никогда не доказывает, но полезен как игра и упражнения. Софизм учит думать и критично подходить к своим и чужим ** В этом примере полный стакан рассуждениям. это 100%, а пустой – 0%. Половина полного стакана равна 100% : 2 = 50%, Половина пустого стакана равна 0% : 2 = 0, то есть < 50%. Таким образом ни одна строка софизма не может быть верной. Укажите преобразования, нарушающие ОДЗ? В этом софизме смешиваются понятия. А сам софизм рассчитан на потерю нити рассуждений при повторении сходных по звучанию слов, относящихся к разным величинам. Будьте внимательны!

Учись учиться - весело играя! Игра 8. Что такое Оксюморон? Придумай примеры. Оксю морон, окси морон (от древнегреческого слова) - приём, который используется в литературе для создания стилистического эффекта и усиления эмоционального накала строки: -Кого позвать мне? С кем мне поделиться Той грустной радостью, что я остался жив? (С. Есенин) В устной речи может использоваться для «объяснения необъяснимой ситуации» . Часто бывает ответом на Риторический вопрос. Полезен в безвыходном положении. Играет роль юмористической отговорки. Ярко характеризует говорящего. -У нас тут начальство немножко вышло… Давайте мы Вам попозже перезвоним? Придумайте свои -Ну, а теперь-то точно придёшь? -Наверное точно. примеры. Что общего с Софизмами?

Учись учиться - весело играя! Игра 9. Про весёлый Оксюморон и умную Аксиому Почему один называют «остроумной глупостью» , а другое – «прописной истиной» ? Как рождается переносный смысл? Зачем нужны прописные истины? Попробуйте дополнить и дословно показать первую фразу примера в форме маленькой театральной сценки? Можете написать к ней несколько сценариев? Сколько сценариев у вас получится? Если бы математика утонула в переносных смыслах? Сколько чисел в математике? Сколько видов геометрических фигур? Формул? Что будет если обо всех закономерностях начать говорить в переносном смысле? Как математики дружат с конкретикой? Как конкретика помогает в жизни? Когда нужны ответы «Да» и «Нет» ? Как сделать из этих фраз Аксиому? Сколько тут выйдет Аксиом? ПРИМЕРЫ: «Труд сделал из обезьяны человека, а лень – превращает в …» «Человек – биологический вид с богатыми умственными возможностями» .

Учись учиться - весело играя! Игра 10. Как придумать Аксиому? Где тут Аксиома? ? ? 1) Небо – всегда голубое. 2) Небо имеет голубой или синий оттенок. 3) Перед дождём небо пасмурное. 4) Днём и ночью небо разного цвета.

Учись учиться - весело играя! Вспомните, каким бывает небо? ? ? Что назвать Аксиомой и какие ей предстоят Отборочные испытания? Каждая Аксиома проходит проверку. Каждая Аксиома имеет научное объяснение. Каждая Аксиома проста и к ней обращаются за помощью в более сложных задачах. Каждая аксиома Абсолютно верна и помогает понять любые частные случаи.

Учись учиться - весело играя! 1) 2) 3) 4) Где тут Аксиома? ? ? Небо – всегда голубое. Но ночью небо синее. А в бурю оно пасмурное. Небо имеет голубой или синий оттенок Перед дождём небо пасмурное. Но бывает слепой дождик – он идёт в ясную погоду. Днём и ночью небо разного цвета. Но бывают белые ночи, когда светло. И бывают такие пасмурные дни, что даже похожи на белые ночи. Научное объяснение голубизны неба: Небо имеет голубой или синий оттенок потому, что синяя часть солнечного спектра сильнее рассеивается в атмосфере. Синие и фиолетовые лучи имеют больший коэффициент преломления и проникают в атмосферу даже когда другая часть солнечного света

Учись учиться - весело играя! И даже при изменениях погоды, в разное время суток и в разных метеоусловиях в окраске атмосферы присутствуют сине-голубые оттенки. Найди их на картинке! Чтоб красиво рисовать … нужно много-много знать!!!

Учись учиться - весело играя! Как живут Аксиомы в математике? Что зовут Аксиомой? Аксио ма (др. -греч. — утверждение, положение), постулат — исходное положение теории, принимаемое в рамках данной теории истинным без требования доказательства. Аксиома должна быть: 1. Истинной при любых условиях, без исключений и ограничений. 2. Простой, понятной и наглядной. Её истинность можно проверить и понять на примерах. 3. Наиболее важной «частью» изучаемой науки. Поэтому нужно верно понимать аксиомы. Что не позволено Аксиоме? 1. Содержать противоречия, а также взаимоисключающие слова или предложения. 2. Предполагать исключения. Так фраза «любое исключение из правила только подтверждает это правило» - это Оксюморон и к Аксиомам не применим. 3. 3. Правила не могут называться Аксиомами. Правила имеют статистический характер (как правило, чаще всего, в большинстве случаев, наиболее вероятно, почти всегда за редким исключением…) Правила могут меняться и отменяться, а Аксиома - верна всегда. Аксиома понятней, чем Правило!!!

Учись учиться - весело играя! Игра 11. Что будет, если Математический Чертёж повернуть «вниз головой» ? Боком? На угол? Нарушится ли истинность чертежа при повороте листа бумаги? Правда ли что повернув Квадрат, мы получаем Ромб? Был

Учись учиться - весело играя! Игра 12. Имеем право проверить Аксиому! Вдумайтесь в простые примеры аксиом, нарисуйте или покажите в пространстве: Представьте, что кто-то ошибся и нарушил Аксиому. Как это могло произойти? Помогите найти и

Математика и Жизнь Аксиома Архимеда о том, как «вода камень точит» M < m*N, где M, m - большое и малое числа, а N – множитель Глядя на ручей, пробивающийся в камнях, Архимед сравнил каплю воды с маленьким числом, которое при многократном умножении способно победить любое, даже самое большое число. Архимед сформулировал это так: «Нет такого маленького, которое при многократном умножении не превысило бы любого большого, каким бы большим оно ни казалось. Вопрос лишь в количестве повторов. Так жизнь состоит из мелочей, которые повторяясь суммируются в грандиозные причины и меняют наш мир» . Проверим математическую часть высказывания? А о философии подумайте сами. 1) Выберем маленький отрезок. (Например можно взять 1 см, 1 клетку, полклетки) 2) Выберем большой отрезок (Например: 5 клеток, 5 см, 10 см, 15 см…) Можно даже несколько. 3) Сколько раз подряд надо выложить маленький отрезок, чтобы получить цепочку длиннее большого отрезка?

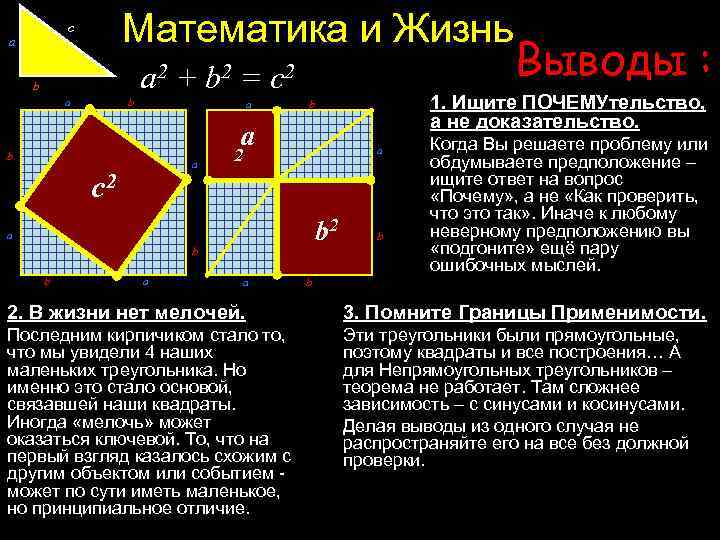Математика и Жизнь c a a 2 b a + b 2 = b c 2 a 1. Ищите ПОЧЕМУтельство, а не доказательство. b a c 2 a 2 b 2 a b b a a b Выводы : b Когда Вы решаете проблему или обдумываете предположение – ищите ответ на вопрос «Почему» , а не «Как проверить, что это так» . Иначе к любому неверному предположению вы «подгоните» ещё пару ошибочных мыслей. 2. В жизни нет мелочей. 3. Помните Границы Применимости. Последним кирпичиком стало то, что мы увидели 4 наших маленьких треугольника. Но именно это стало основой, связавшей наши квадраты. Иногда «мелочь» может оказаться ключевой. То, что на первый взгляд казалось схожим с другим объектом или событием - может по сути иметь маленькое, но принципиальное отличие. Эти треугольники были прямоугольные, поэтому квадраты и все построения… А для Непрямоугольных треугольников – теорема не работает. Там сложнее зависимость – с синусами и косинусами. Делая выводы из одного случая не распространяйте его на все без должной проверки.

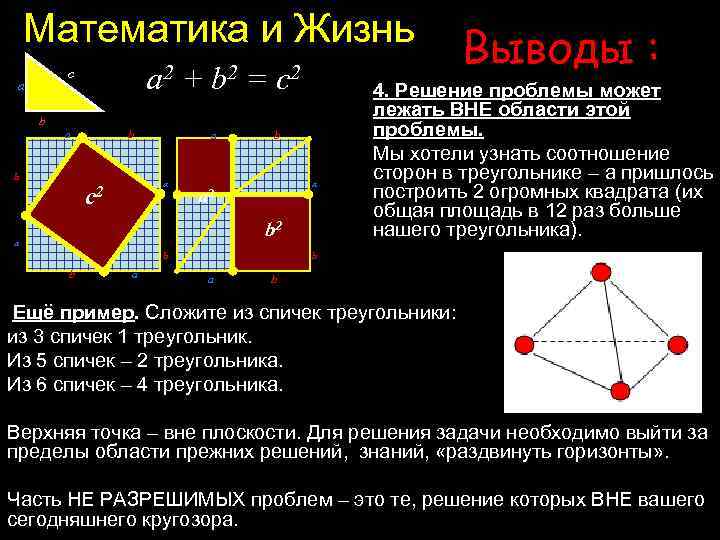Математика и Жизнь a 2 + b 2 = c 2 c a b b a a c 2 b a a 2 b 2 a b b a Выводы : 4. Решение проблемы может лежать ВНЕ области этой проблемы. Мы хотели узнать соотношение сторон в треугольнике – а пришлось построить 2 огромных квадрата (их общая площадь в 12 раз больше нашего треугольника). b a b Ещё пример. Сложите из спичек треугольники: из 3 спичек 1 треугольник. Из 5 спичек – 2 треугольника. Из 6 спичек – 4 треугольника. Верхняя точка – вне плоскости. Для решения задачи необходимо выйти за пределы области прежних решений, знаний, «раздвинуть горизонты» . Часть НЕ РАЗРЕШИМЫХ проблем – это те, решение которых ВНЕ вашего сегодняшнего кругозора.

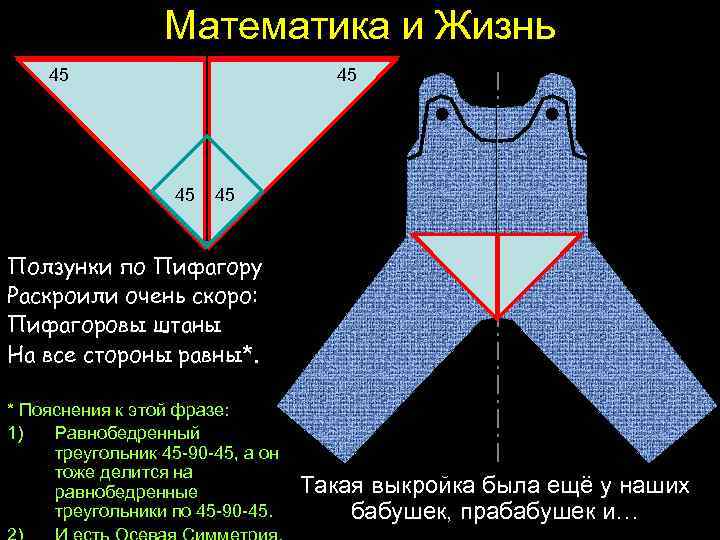Математика и Жизнь 45 45 45 Ползунки по Пифагору Раскроили очень скоро: Пифагоровы штаны На все стороны равны*. * Пояснения к этой фразе: 1) Равнобедренный треугольник 45 -90 -45, а он тоже делится на равнобедренные треугольники по 45 -90 -45. Такая выкройка была ещё у наших бабушек, прабабушек и…

Логические задачки Трое разбойников делят клад в лесу. Как им разделить его, не поссорившись, если ни подсчитать, ни взвесить, ни иначе оценить стоимость каждой доли клада они не могут?

Логические задачки На квадратной веранде вдоль каждой стороны нужно поставить вазоны с цветами. Какое минимальное количество вазонов потребуется, чтобы вдоль каждой стены стояло по 3 вазона?

Логические задачки А (город честных) В (город лгунов) В математической стране есть два города: город, где все жители говорят правду (А), и город В, где все жители всегда лгут. Жители обоих городов ходят друг к другу в гости. Вы – путник, который путешествует по математическим просторам и случайно попали в один из этих городов. Как задав единственный вопрос первому встречному, безошибочно понять в каком именно городе Вы оказались? Вариант ответа: «Вы житель этого города? » Если ответ «Да» - то Вы в городе А. Если ответ «Нет» - то в городе В. * А если задать другой вопрос: «Вы житель города А? » В городе А местные скажут «да» , потому что говорят правду, а пришлые скажут «да» потому что лгут. В городе В местные скажут «да» потому что лгут, а пришлые ответят «да» потому что говорят правду. В итоге все на этот вопрос ответят одинаково, и понять в каком городе Вы находитесь это не поможет. Это не решение задачи.

Логические задачки 1 -я 2 -я 3 -я 4 -я 5 -я 6 -я На прямой стоят 6 точек на равном расстоянии друг от друга. Каково расстояние от первой до последней, если расстояние между соседними точками 10 см? (Обычно дети не догадываются сделать чертёж и ошибаются, считая что это равно 6 х 10 = 60 см) Пояснения: от 1 -ой точки до 6 -ой будет 5 расстояний!!! Не спешите умножать, сначала думайте!!! Ответ 50 см.

Развитие сообразительности Не отрывая руки нарисуйте эту картинку. Выполните задание, не проходя повторно по уже проведённым линиям. Сколько найдёте решений? С какой точки лучше стартовать в процессе поиска?

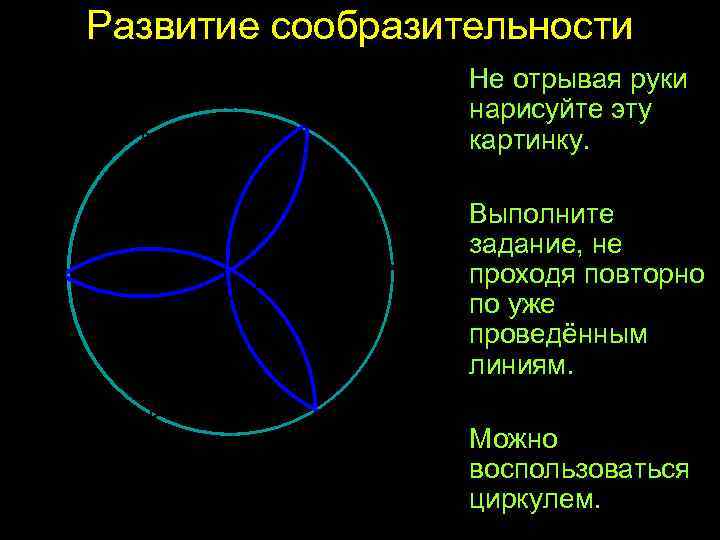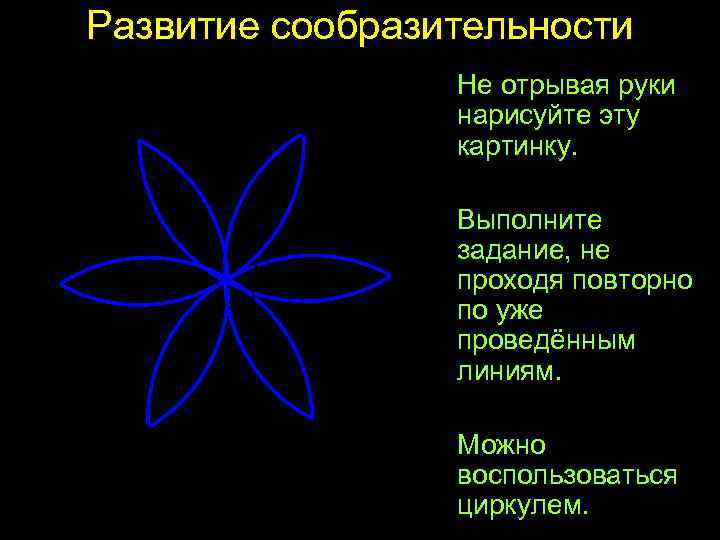Развитие сообразительности Не отрывая руки нарисуйте эту картинку. Выполните задание, не проходя повторно по уже проведённым линиям. Можно воспользоваться циркулем.

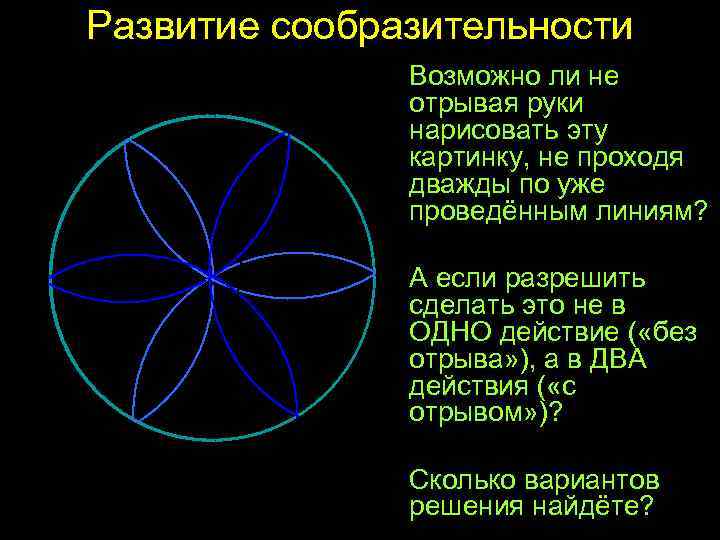Развитие сообразительности Возможно ли не отрывая руки нарисовать эту картинку, не проходя дважды по уже проведённым линиям? А если разрешить сделать это не в ОДНО действие ( «без отрыва» ), а в ДВА действия ( «с отрывом» )? Сколько вариантов решения найдёте?

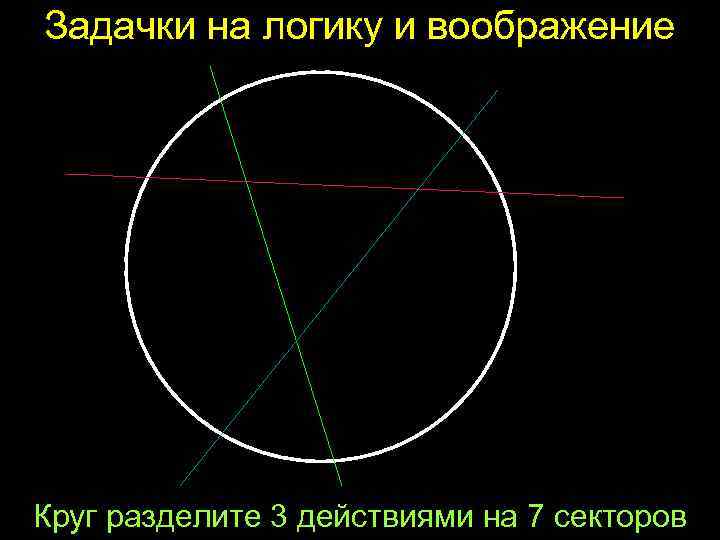Задачки на логику и воображение Круг разделите 3 действиями на 7 секторов

Задачки на логику и воображение ? ? ? Круг разделите 3 действиями на 8 секторов

Какие бывают линии в математике? 1. Какие ещё могут быть линии, кроме прямых? Какие линии любит математика? -Линия провисания цепочки или верёвочки (парабола), - Линия, по которой летит волан в бадминтоне или камешек брошенный под углом к горизонту (парабола) -Линия волны на поверхности воды (синусоида), -Линия, по которой прилетает к нам Комета Галлея (гипербола) - Линия, по которой летит вода из водяного пистолетика или из брызгалки (парабола) - Линия, по которой вытекает вода из лейки или из дырявой ёмкости на даче (парабола) - Линия, по которой заворачивает трамвай, форма рельсов на повороте (парабола) - Линия сводов куполов, арок и прочих архитектурных строений, напоминающая носик яичной скорлупы (парабола)

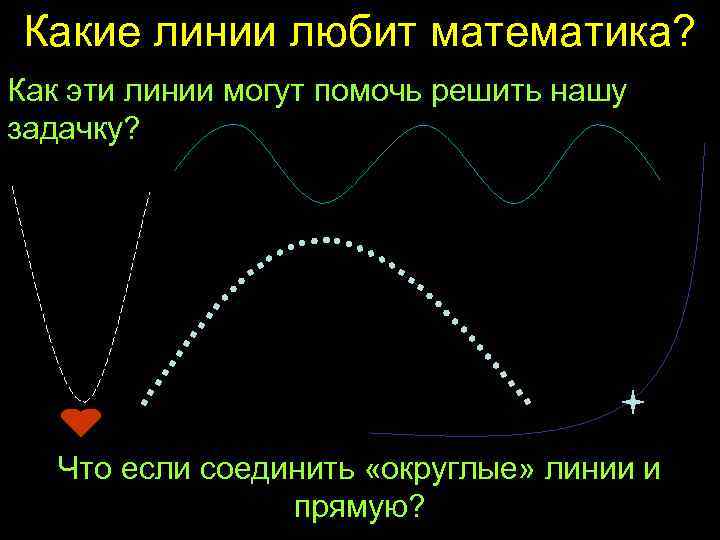Какие линии любит математика? Как эти линии могут помочь решить нашу задачку? Что если соединить «округлые» линии и прямую?

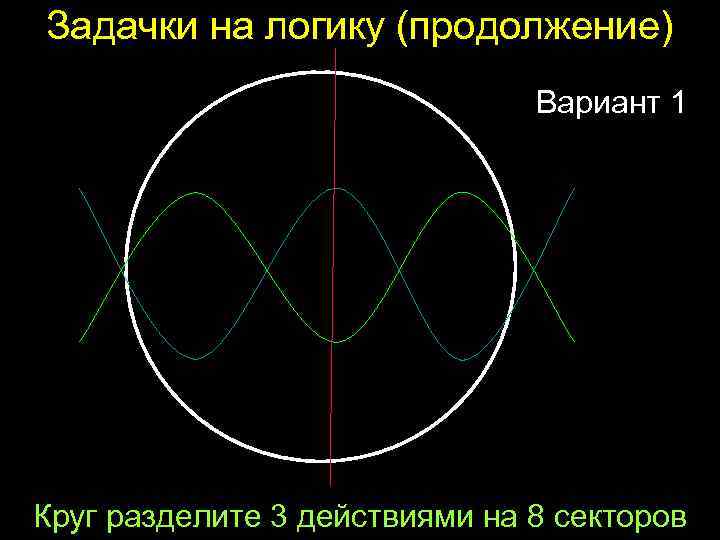Задачки на логику (продолжение) Вариант 1 Круг разделите 3 действиями на 8 секторов

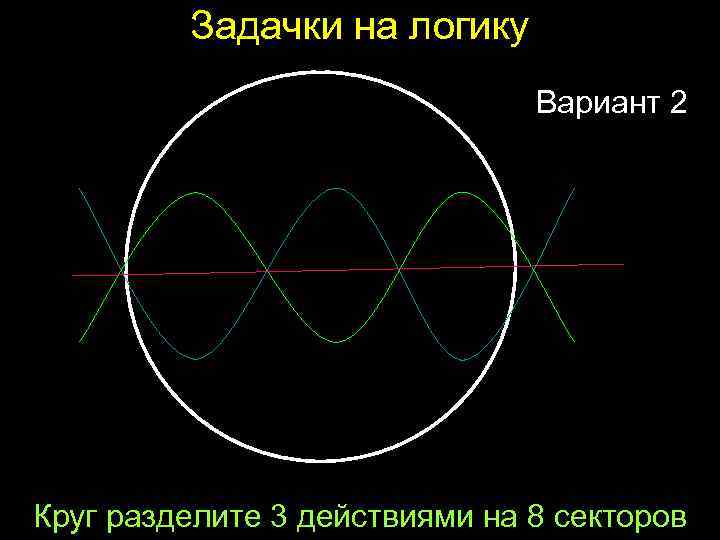Задачки на логику Вариант 2 Круг разделите 3 действиями на 8 секторов

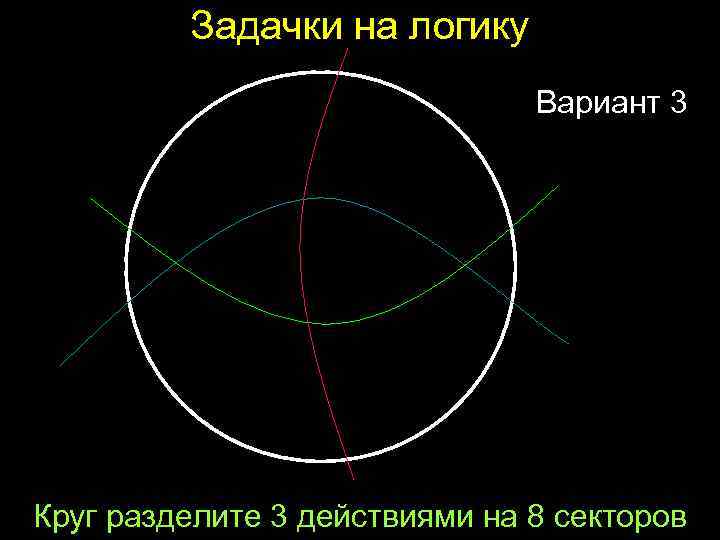Задачки на логику Вариант 3 Круг разделите 3 действиями на 8 секторов

Задачки на логику А если всего 1 линию направить «по другому» - 6 секторов

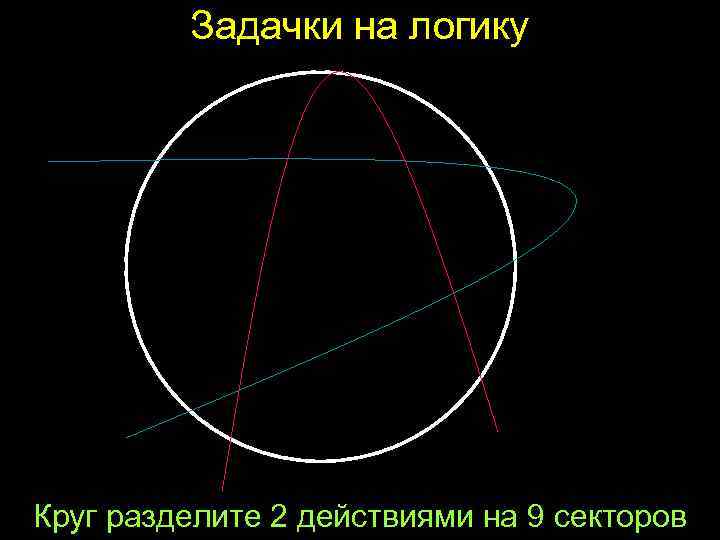Задачки на логику Круг разделите 2 действиями на 9 секторов

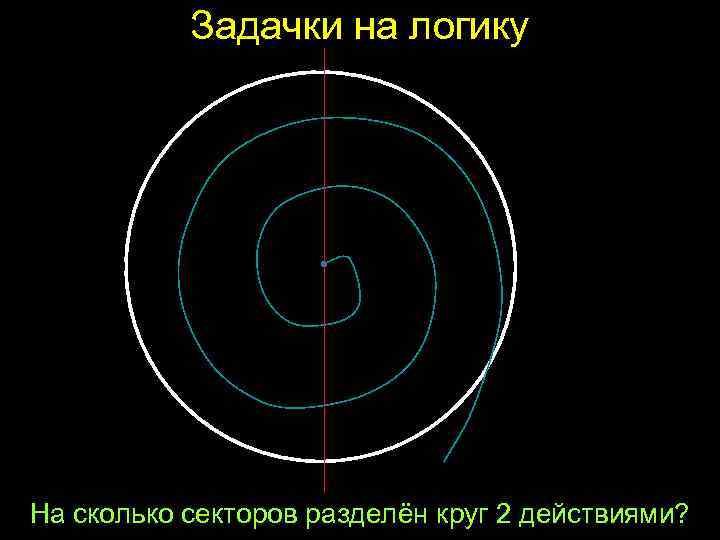Задачки на логику На сколько секторов разделён круг 2 действиями?

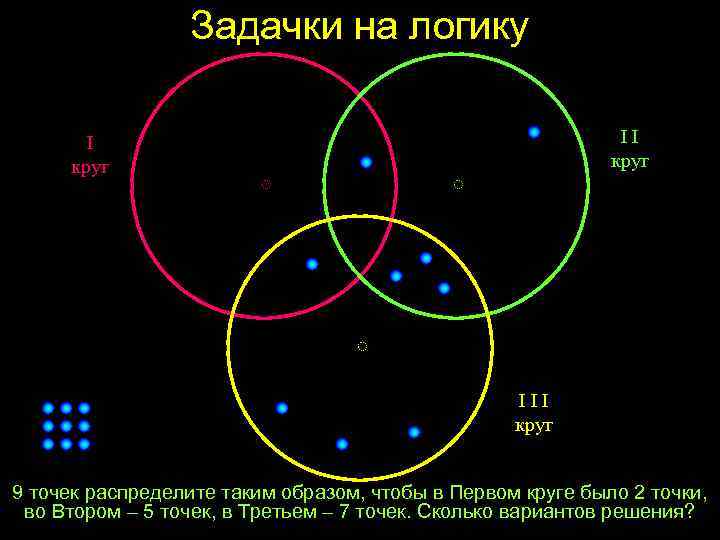Задачки на логику II круг III круг 9 точек распределите таким образом, чтобы в Первом круге было 2 точки, во Втором – 5 точек, в Третьем – 7 точек. Сколько вариантов решения?

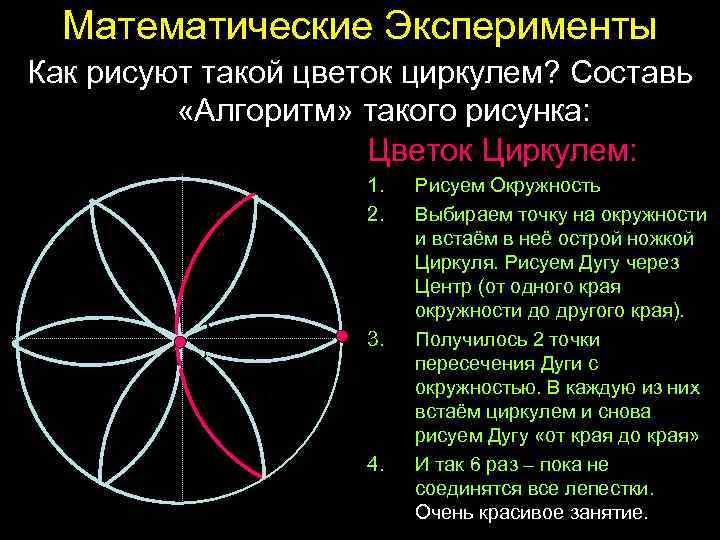Математические Эксперименты Как рисуют такой цветок циркулем? Составь «Алгоритм» такого рисунка: Цветок Циркулем: 1. 2. 3. 4. Рисуем Окружность Выбираем точку на окружности и встаём в неё острой ножкой Циркуля. Рисуем Дугу через Центр (от одного края окружности до другого края). Получилось 2 точки пересечения Дуги с окружностью. В каждую из них встаём циркулем и снова рисуем Дугу «от края до края» И так 6 раз – пока не соединятся все лепестки. Очень красивое занятие.

Математические Эксперименты Цветочки, Погрешность и Открытие числа «Пи» В таком цветочке часто «остаётся» пара миллиметров и 6 -й лепесток чуть больше остальных. Ошибка. Но именно эта погрешность вдохновила античных математиков искать ответ на вопрос «Во сколько раз окружность длиннее радиуса? В 6 с хвостиком раз. Во сколько раз длина полукруглой арки превосходит её высоту? В 3 с хвостиком…» Для построения храмов и арок, украшенных лепниной, нужно было знать точно. Если аккуратно разделить «Окружность на Диаметр» - то получим не ровно 3, а с тоненьким хвостиком 3, 14159… Своим «длинным хвостиком» число напоминает Мышку; первой цифрой «троечкой» – мышиные ушки; и даже называется «Пи» . Может математики так пошутили?

Игры на координатной плоскости «Морской бой» , «Шахматы» , «Шашки» , «Уголки» , «Крестикинолики» и т. д. В эти игры очень полезно играть всем! В таких играх важны не только буквы и цифры, которые являются вариантом плоскости координат. В этих играх присутствует и логическая организация пространства: привлекательность определённых клеток, перспективность хороших связок и комбинаций, логика принятия решений.

Морской бой – игра на понимание координат Развивающей игра становится при полноценной обратной связи. Чем больше угадываний – тем меньше развития. Кроме слов «мимо» и «попал» следует использовать термины «ранил» и «убил» . Эти данные необходимы для правильных логических рассуждений ребёнка. Кроме того, в случае попадания в корабль торпеды ( «ранил» ) надо честно говорить «у меня тут 3 -х палубный» или «у меня тут 5 -палубный корабль» . Это тоже необходимые данные для логических рассуждений ребёнка. Вы ведь учите думать, а не угадывать.

Какой была Таблица Пифагора? 2 х 2 = 2 строчки по 2 точки, 3 х 3 = 3 строчки по 3 точки, 4 х 4 = 4 строчки по 4 точки, 5 х 5 = 5 строчек по 5 точек, … Таблица точек и никаких цифр!!! Понятно и наглядно! 4) Покажи «Квадрат числа» Что такое квадрат числа? Это квадрат на картинке! Почему говорят «квадрат двойки» , « 2 в квадрате» ? Чему равно 3 в квадрате? Придумай свои примеры квадратов числа. Как можно придумать записывать число в квадрате? Что значит 32=9?

Какой была Таблица Пифагора? 2 х 2 = 2 строчки по 2 точки, 3 х 3 = 3 строчки по 3 точки, 4 х 4 = 4 строчки по 4 точки, 5 х 5 = 5 строчек по 5 точек… … Таблица точек и никаких цифр!!! Понятно и наглядно! 5) Сложи ладошку «уголком» и Покажи Квадратный корень «Зри в корень» = «смотри в суть» . Корень квадрата числа. Надо разобрать квадрат до основ. Основа - это сторона, сколько точек. Ведь если квадрат на 2 точках (2 по 2) то это всегда 4, если квадрат на 3 точках (3 по 3) – то это всегда 9, на 4 точках - то 16. «Корень» = на скольких точках выстроен квадрат. Как «найти» любой корень по такой табличке точек?

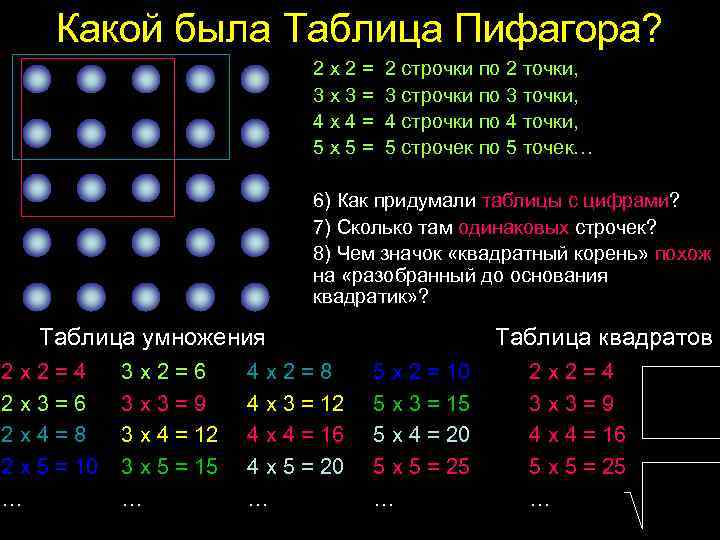Какой была Таблица Пифагора? 2 х 2 = 2 строчки по 2 точки, 3 х 3 = 3 строчки по 3 точки, 4 х 4 = 4 строчки по 4 точки, 5 х 5 = 5 строчек по 5 точек… 6) Как придумали таблицы с цифрами? 7) Сколько там одинаковых строчек? 8) Чем значок «квадратный корень» похож на «разобранный до основания квадратик» ? Таблица умножения 2 х 2 = 4 2 х 3 = 6 2 х 4 = 8 2 х 5 = 10 … 3 х 2 = 6 3 х 3 = 9 3 х 4 = 12 3 х 5 = 15 … 4 х 2 = 8 4 х 3 = 12 4 х 4 = 16 4 х 5 = 20 … Таблица квадратов 5 х 2 = 10 5 х 3 = 15 5 х 4 = 20 5 х 5 = 25 … 2 х 2 = 4 3 х 3 = 9 4 х 4 = 16 5 х 5 = 25 …

Какой была Таблица Пифагора? 1 2 3 4 5 6 7 8 9 10 … 1 2 3 4 5 6 7 8 9 10 11 12 … 9) Песенка про «Пифагоровы штаны» – это Переместительн ый закон умножения: 3 х9=9 х3 3 х 9 = 27 Жёлтый прямоугольник 9 х 3 = 27 Зелёный Прямоугольник

Теоремы? Это просто! c a a 2 + b 2 = c 2 b a Смотри! b a a b 2 c a b a a 2 2 b b b a b Пифагор взял треугольник со сторонами 3, 4, 5. 9 + 16 = 25. Всегда ли a 2 + b 2 = c 2? Чтобы понять и проверить он сделал простой и гениальный чертёж. А рядом – одно

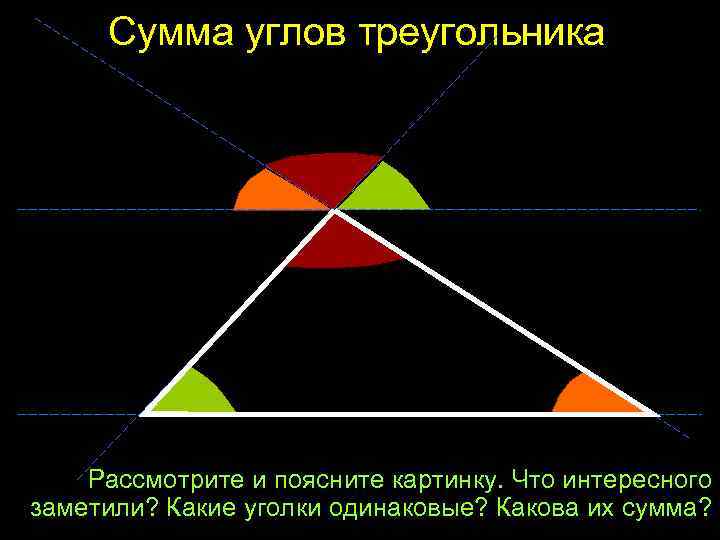Сумма углов треугольника Рассмотрите и поясните картинку. Что интересного заметили? Какие уголки одинаковые? Какова их сумма?

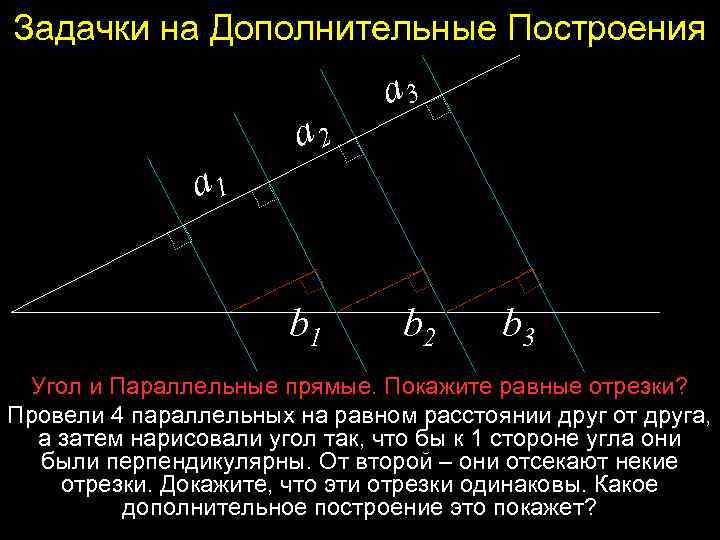Задачки на Дополнительные Построения a 2 a 3 a 1 b 2 b 3 Угол и Параллельные прямые. Покажите равные отрезки? Провели 4 параллельных на равном расстоянии друг от друга, а затем нарисовали угол так, что бы к 1 стороне угла они были перпендикулярны. От второй – они отсекают некие отрезки. Докажите, что эти отрезки одинаковы. Какое дополнительное построение это покажет?

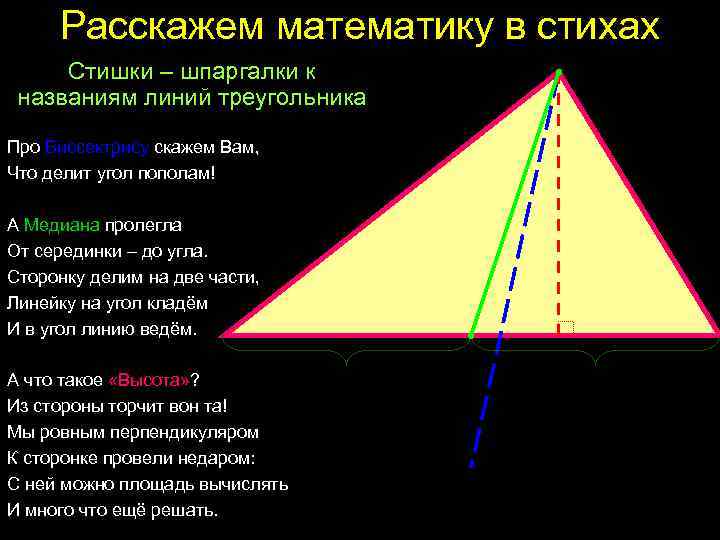Расскажем математику в стихах Стишки – шпаргалки к названиям линий треугольника Про Биссектрису скажем Вам, Что делит угол пополам! А Медиана пролегла От серединки – до угла. Сторонку делим на две части, Линейку на угол кладём И в угол линию ведём. А что такое «Высота» ? Из стороны торчит вон та! Мы ровным перпендикуляром К сторонке провели недаром: С ней можно площадь вычислять И много что ещё решать.

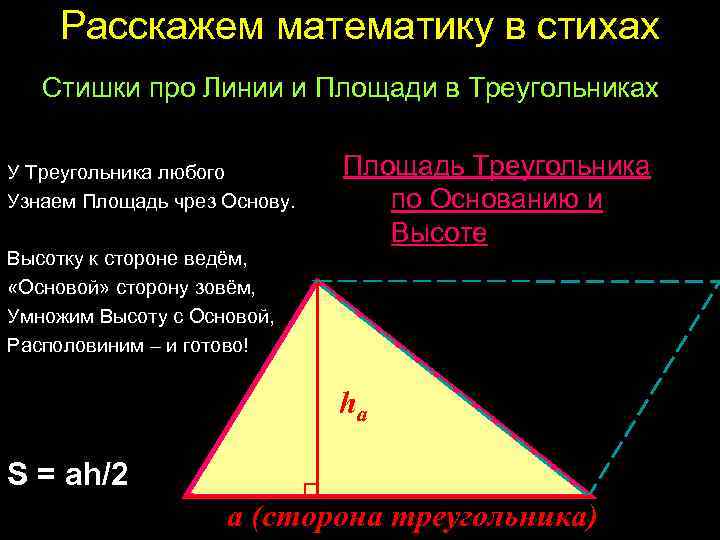Расскажем математику в стихах Стишки про Линии и Площади в Треугольниках У Треугольника любого Узнаем Площадь чрез Основу. Высотку к стороне ведём, «Основой» сторону зовём, Умножим Высоту с Основой, Располовиним – и готово! Площадь Треугольника по Основанию и Высоте ha S = ah/2 a (сторона треугольника)

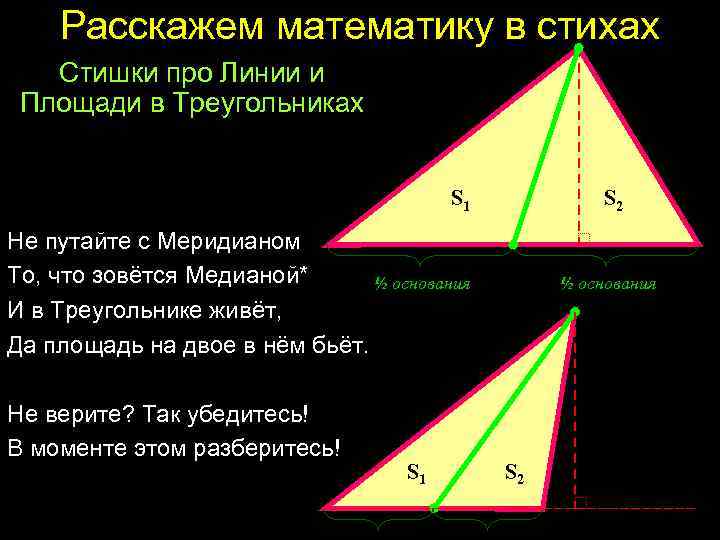Расскажем математику в стихах Стишки про Линии и Площади в Треугольниках S 1 = S 2 S 1 S 2 Не путайте с Меридианом То, что зовётся Медианой* ½ основания И в Треугольнике живёт, Да площадь на двое в нём бьёт. ½ основания S 1 = S 2 Не верите? Так убедитесь! В моменте этом разберитесь! S 1 S 2

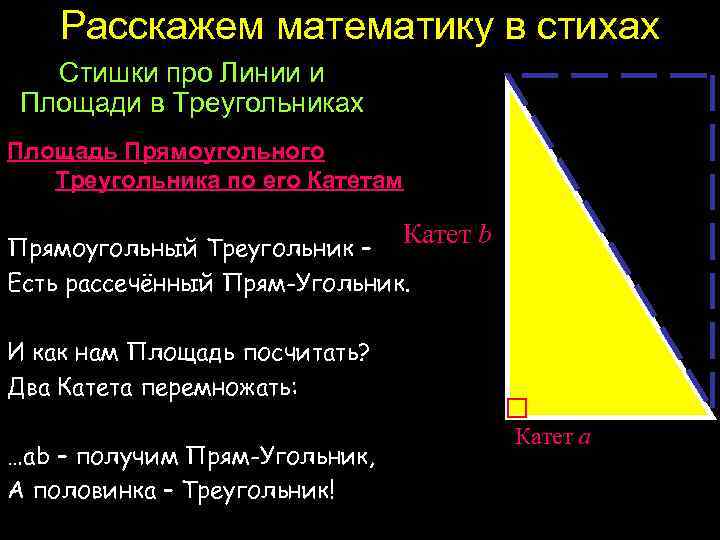Расскажем математику в стихах Стишки про Линии и Площади в Треугольниках Площадь Прямоугольного Треугольника по его Катетам Катет b Прямоугольный Треугольник – Есть рассечённый Прям-Угольник. И как нам Площадь посчитать? Два Катета перемножать: …ab – получим Прям-Угольник, А половинка – Треугольник! Катет a

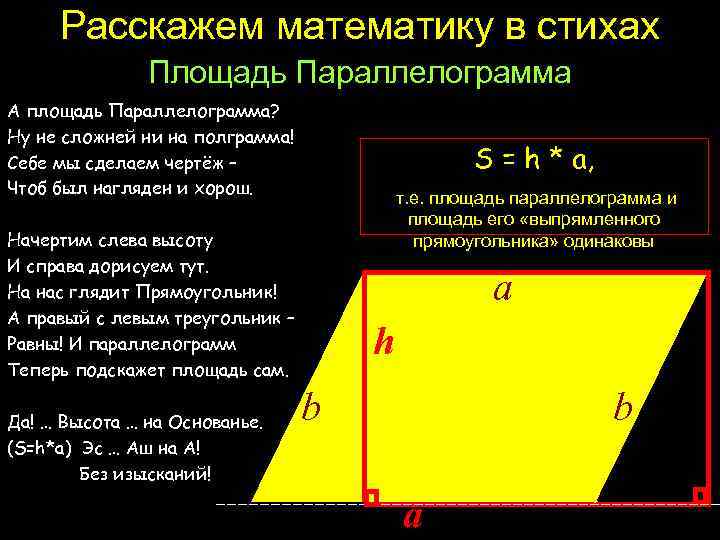Расскажем математику в стихах Площадь Параллелограмма А площадь Параллелограмма? Ну не сложней ни на полграмма! Себе мы сделаем чертёж – Чтоб был нагляден и хорош. S = h * a, т. е. площадь параллелограмма и площадь его «выпрямленного прямоугольника» одинаковы Начертим слева высоту И справа дорисуем тут. На нас глядит Прямоугольник! А правый с левым треугольник – Равны! И параллелограмм Теперь подскажет площадь сам. Да! … Высота … на Основанье. (S=h*a) Эс … Аш на А! Без изысканий! a h b b a

Что Вы знаете о математике? (I) 1. Назовите науку, которую за 500 лет до нашей эры создали Древние Греки, а теперь спустя тысячелетия всё человечество изучает в школе их труды в том же самом виде. Науку, не устаревшую за 2500 лет. 2. За 300 лет до нашей эры Александрийский учёный написал 15 книг об этой науке, которые составляют основу школьной программы даже сегодня. Кто автор этих книг и что это за книги? 3. Письменность для этой науки создавалась всеми народами, но самой распространенной стала арабская запись. Вторая по известности – римская. Что это за письменность? Продемонстрируйте её. 4. В 16 -17 веках были сделаны открытия, которые сегодня входят в программу каждого учебника 7 -11 класса. В школьной программе нет ничего сложного. Но люди продолжают жаловаться на сложность этого предмета, забывая, что с первых лет жизни ежедневно им пользуются. Что это за предмет? 5. В 19 веке русский учёный Лобачевский дополнил эту науку совершенно новым разделом. Изучают его не в школе, а в специальных ВУЗах. Какую науку дополняли теории Лобачевского и зачем это было нужно?

Кто придумал математику? Пифагор – древний философ и математик, жил в Древней Греции в V-VIвв. до нашей эры. Сделал множество математических открытий. Его имя носит знаменитая Теорема Пифагора. Евклид Александрийский жил в III веке до нашей эры. Собирал и систематизировал знания. Венцом его книги о треугольниках была Теорема Пифагора. Всего получилось 15 книг о математике, где он подробно и интересно рассказал про все фигуры. По его книгам учились, по ним строили храмы, вели расчеты. На протяжении 2500 лет эти знания являются основными и пополняются новыми открытиями.

Кто придумал математику? Рене Декарт 16 -17 вв. – изобрёл координатный метод и ввёл удобную систему координат, которую мы используем до сих пор. Заложил основы векторной алгебры. Пьер Ферма – 17 век, один из создателей аналитической геометрии и математического анализа, теории чисел и теории вероятностей. Наибольшую известность получил после открытия Теоремы Ферма, названной в его честь.

Гиперболическая геометрия Лобачевского – сложные фигуры: Лобачевский жил в 18 -19 вв. в России, возглавлял Университет и изучал геометрию и физику сложной поверхности. На рисунке - «гравитационная воронка» с эквипотенциальными линиями. Если представить, как маленький шарик катится вниз вдоль одной из «вертикалей» - то в каждую секунду он будет пролетать всё большее расстояние по этой поверхности и будет оказываться на следующей горизонтальной полоске. В геометрии Лобачевского есть много других сложных фигур. Риман жил в 19 веке и тоже дополнил геометрию своими открытиями. Описывая эллиптические пространства, он обобщил свою теорию с открытиями Лобачевского и получилась «Неевклидова Геометрия Сложных Многомерных Пространств» . Её изучают в ВУЗах.

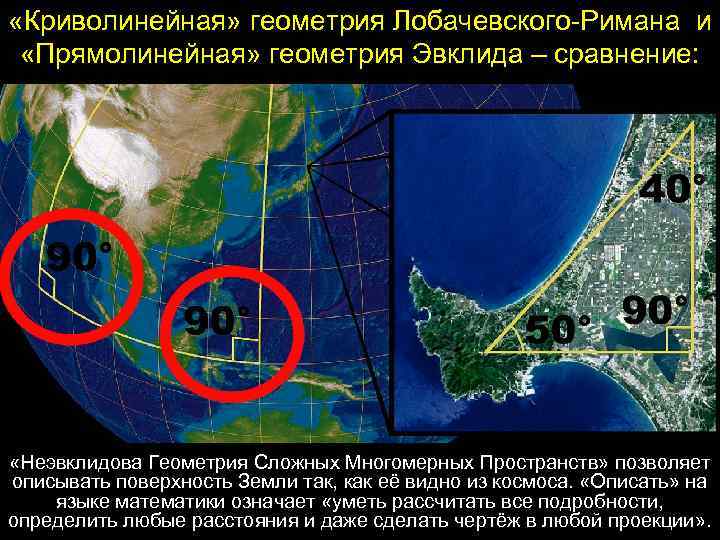«Криволинейная» геометрия Лобачевского-Римана и «Прямолинейная» геометрия Эвклида – сравнение: «Неэвклидова Геометрия Сложных Многомерных Пространств» позволяет описывать поверхность Земли так, как её видно из космоса. «Описать» на языке математики означает «уметь рассчитать все подробности, определить любые расстояния и даже сделать чертёж в любой проекции» .

Теория Вероятности = НЕ Гарантия? ! Как вычисляют Вероятность? 1. Вероятность совпадения событий всегда равна произведению Вероятностей. 2. Любая Вероятность всегда меньше 1 (меньше 100%). Поэтому произведение вероятностей - всегда намного меньше, чем исходные вероятности. ПРИМЕР 1. Допустим, вероятность чего-либо 50%. Какова вероятность того, что такое событие произойдёт дважды? Это не 50%, а 0, 5 х 0, 5 = 0, 25 = 25%. А какова вероятность что такое событие совпадет трижды? 0, 5 х 0, 5 = 12, 5%. А четырежды? Всего 6%. Удивлены? Проверьте сами! ПРИМЕР 2. Какова вероятность того, что Вы успеете на поезд, если вышли из дома без запаса времени, а надо ещё сделать пару пересадок на транспорте? Даже если вероятность быстро сесть в транспорт равна 50%, то вероятность успеть в двух местах пересадки – уже не выше 25%, а вероятность опоздать – аж 75%. И это не «Закон подлости» - это умножение вероятностей. А ещё есть светофоры и прочие факторы, уменьшающие вероятность желаемого события… ПРИМЕР 3. Легко ли угадать 2 из 10 ? Допустим, что у Вас 10 камешков, из них 2 синих. Играя в камешки, Вы случайным образом выбрасываете каждый раз 1 камешек. Какова вероятность того, что дважды подряд выпадет именно синий? 2 : 10 = 0, 2 (20%) – вероятность того, что выпадет 1 синий. И камешков уже не 10, а 9. 1 : 9 = 0, 11 (11%) – вероятность того, что выпадет 2 синий. Но не думайте что это ответ! Ведь теперь надо рассчитать вероятность совпадения этих событий!!! 0, 2 х 0, 11 = 2% - так низка вероятность угадать 2 элемента из 10 … А Вы думали 20%? Вы ошиблись в 10 раз!!! Поэтому математики не играют в азартные игры.

Что Вы знаете о математике? (II) 6. Кто из математиков стал знаменит своим литературным или музыкальным творчеством? Кто из математиков знаменит архитектурными достижениями? Живописью? Фресками? Мозаиками? Что Вы знаете о богатстве талантов гениальных математиков? Почему говорят, что Гений талантлив во всём! 7. В каких веках родилась мода на «романтиков, чуждых наукам» ? Почему? Кому была нужна легенда о несовместимости физики и лирики? 8. Что Вы знаете о бардах? Почему среди них всегда много людей с физико-математическим образованием? 9. Кто и почему сказал: «Математика царица наук» ? Подсказка: Карл Фридрих Гаусс – немецкий физик, живший в конце 18 -первой половине 19 века. Он изобрёл универсальный метод решения систем уравнений со многими неизвестными, который получил название «Метода Гаусса» . Осталось ответить на главный вопрос – почему физик назвал «Царицей» математику? 10. А что лично Вам нравится в Математике? Какие разделы понравились? Что бы хотелось увидеть ещё?

Как сделать математика поэтом? Любовь к математике может быть разной! Любовь к математике может быть разной: Большой; Избирательной; ЦЕЛЕ - сообразной; - Любовь к Вычисленьям; - К задачам без Цифр; - Любовь к Построеньям; - Разгадывать Шифр; Кому-то милее Загадки, Софизмы – Здесь каждый найдёт Для желанной харизмы! Есть шоу - «угадывать числа и мысли» , Есть игры – полны потаённого смысла: Играть в «Морской бой» каждый ведь рад? Система Декартовых координат! Шашки и Шахматы – с Логикой дружат, Читать Детективы – с логикой нужн Кроссворды разгадывать, Платьица шить… Выводы? С Логикой радостней жить А если уж с логикой полный порядо – Пусть будет порядок у Ваших тетрадок: На листике в клетку рисуем чертёж Задачка решилась – и вечер хорош Победа в задаче – не просто удача А опыт и логика с нею в придачу. «Чуйка» растёт по мере побед – И нету надёжней страховки от бед. Любовь к математике может быть