Математика в Древнем Египте Древний Египет

Математика в Древнем Египте

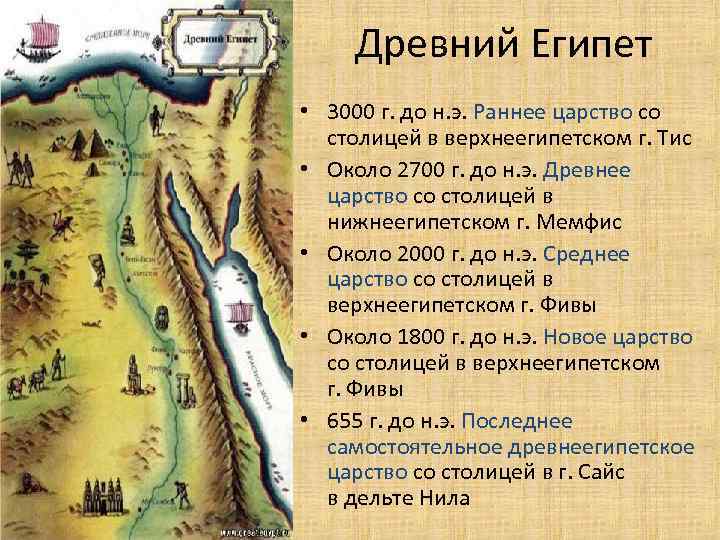Древний Египет • 3000 г. до н. э. Раннее царство со столицей в верхнеегипетском г. Тис • Около 2700 г. до н. э. Древнее царство со столицей в нижнеегипетском г. Мемфис • Около 2000 г. до н. э. Среднее царство со столицей в верхнеегипетском г. Фивы • Около 1800 г. до н. э. Новое царство со столицей в верхнеегипетском г. Фивы • 655 г. до н. э. Последнее самостоятельное древнеегипетское царство со столицей в г. Сайс в дельте Нила

• В эпоху Древнего царства египтяне писали при помощи иероглифов – рисуночного письма, в котором каждый рисунок изображал слова или слог. • В эпоху Среднего царства иероглифическое письмо было заменено более простым иератическим письмом, где от каждого иероглифа осталось несколько характерных штрихов. • В эпоху Нового царства возникло скорописное демотическое письмо.

Математика Древнего Египта Дошедшие до нас древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому наши знания о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов — известно, что греческие математики учились у египтян.

Математика Древнего Египта Основные сохранившиеся источники относятся к периоду Среднего царства, времени расцвета древнеегипетской культуры: • Папирус Ахмеса, или папирус Ринда — наиболее объёмный манускрипт, размером 525 х 33 см, содержащий 84 математические задачи. Написан около 1650 г. до н. э. • Московский папирус, 544 × 8 см (25 задач). Написан около 1850 г. до н. э. • Кожаный свиток, 25 × 43 см. • Папирусы из Лахуна (Кахуна), содержащие ряд фрагментов на математические темы. • Берлинский папирус, около 1300 г. до н. э. • Каирские деревянные таблички (таблички Ахмима). • Папирус Рейснера, примерно XIX век до н. э. От Нового царства до нас дошли несколько фрагментов вычислительного характера. Авторы всех этих текстов неизвестны. Дошедшие до нас экземпляры — это переписанные копии. В Древнем Египте писцы, которые были государственными или храмовыми чиновниками, являлись носителями научных знаний.

Папирус Ахмеса (Папирус Ринда) Все задачи из папируса Ахмеса имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Часть папируса Ахмеса. Британский музей

Московский математический папирус. Государственный музей изобразительный искусств им. А. С. Пушкина

Московский математический папирус

Московский математический папирус

Нумерация (запись чисел) Древнеегипетская нумерация была похожа на римскую: существовали отдельные значки для 1, 100, … 10 000. 10 100 1 000 100 000 1 000 Мерная палка 1 Путы Веревка для обмера полей Цветок лотоса Указательный палец Лягушка Удивленный человек Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему. Иероглифическая запись числа 35736

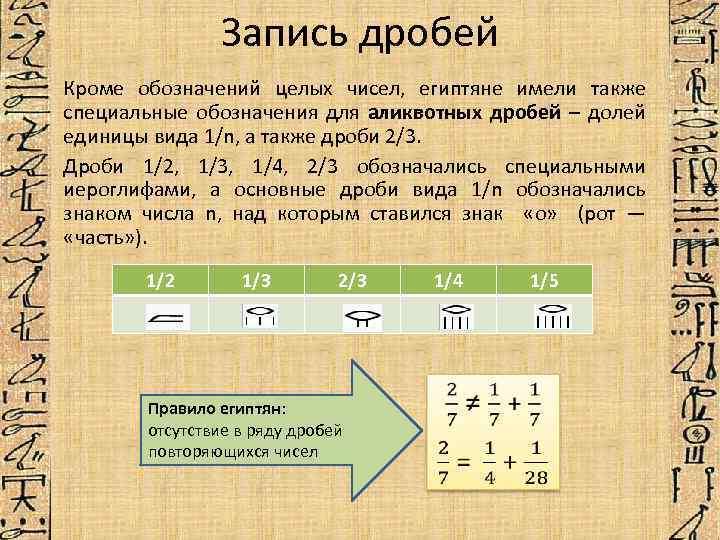Запись дробей Кроме обозначений целых чисел, египтяне имели также специальные обозначения для аликвотных дробей – долей единицы вида 1/n, а также дроби 2/3. Дроби 1/2, 1/3, 1/4, 2/3 обозначались специальными иероглифами, а основные дроби вида 1/n обозначались знаком числа n, над которым ставился знак «ο» (рот — «часть» ). 1/2 1/3 2/3 Правило египтян: отсутствие в ряду дробей повторяющихся чисел 1/4 1/5

Фрагмент кожаного свитка, содержащего перечень простых соотношений между дробями

Арифметика (сложение) Чтобы показать знаки сложения или вычитания, использовался иероглиф или . Первый иероглиф означал сложение (направление ног совпадает с направлением письма), а второй - вычитание. Если при сложении получалось число, большее десяти, тогда десяток записывался повышающим иероглифом.

Арифметика (умножение) При умножении чисел египтяне сначала раскладывали меньший множитель на кратные двойке числа, сумма которых составляет исходное число. Затем они последовательно умножали эти кратные числа на второй множитель (по сути удваивали его несколько раз) и складывали полученные произведения. Пример. Умножим 13 на 238. Раскладываем меньший множитель: 13 = 8 + 4 + 1. Каждое из слагаемых умножаем на 238: ✔ 1 х 238 = 238 2 х 238 = 476 ✔ 4 х 238 = 952 ✔ 8 х 238 = 1904 Складываем полученные произведения: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094.

Умножение и деление Пример умножения. 12 х 12 = 144 Пример деления. 1120 / 80 = 14

Уравнения Египтяне умели записывать и решать уравнения первой степени с одним неизвестным. Такие задачи они называли «аха» . Само слова «аха» означает «куча» , «груда» - здесь в смысле количества, которое неизвестно и его требуется найти. В группе задач «аха» , первых в истории математики отвлеченных задачах, решенных единым методом, мы видим зачатки алгебры как науки о решении уравнений.

Плита с гробницы принцессы Неферетиабет (2590— 2565 до н. э. , Гиза). Лувр (Франция, Париж)

Геометрия. Вычисление площадей Геометрические знания египтян относятся к измерению площадей и объемов. Некоторые найденные при этом результаты были замечательными, но в отдельную отрасль математики геометрия еще не превратилась. Площади треугольников, прямоугольников и трапеций вычитались по точным правилам, в то время как площадь произвольного четырехугольника - по приближенной формуле как произведение полусумм пар противоположных сторон. Этот прием распространялся и на треугольники при d = 0.

Площадь круга Египтяне предполагали, что площадь круга диаметром d равна площади квадрата, сторона которого составляет 8/9 диаметра: Предполагается, что площадь круга диаметром d сравнивается с площадью описанного квадрата, из которого удаляют маленькие квадратики со сторонами (1/6)*d, (1/9)*d, и т. д.

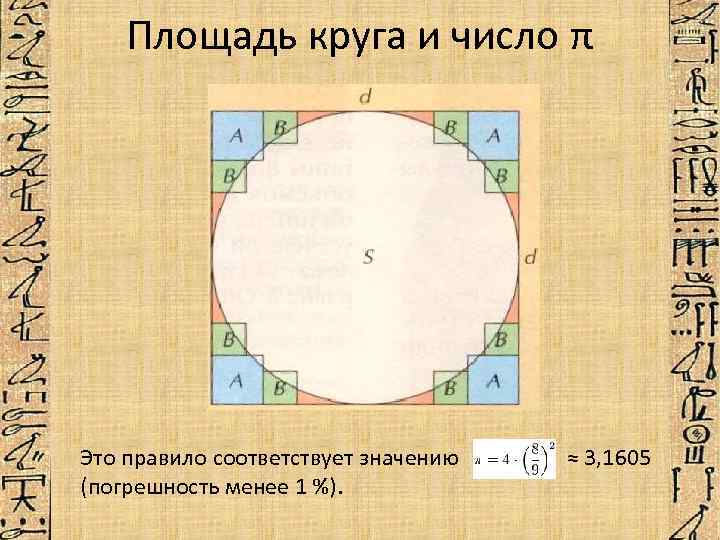Площадь круга и число π Это правило соответствует значению ≈ 3, 1605 (погрешность менее 1 %).

Вычисление обемов Египтяне вычисляли объемы многих тел (куба, цилиндра, призмы, параллелепипеда, умножая площадь основания на высоту. Самым удивительным в геометрии египтян было правило для определения объема усеченной пирамиды. Есть мнение что пирамида разбивалась на части подобным образом: Тогда она составляется из 4 -х пирамид и ее объем равен:

Геометрия Древний свиток папируса, найденный в Оксиринхе, свидетельствует, что египтяне могли вычислять объем усеченного конуса. Эти знания ими использовались для сооружения водяных часов. Известно, что при Аменхотепе III были построены водяные часы в Карнаке. Реконструкция водяных часов по чертежам из Оксиринха Египетским треугольником называется прямоугольный треугольник с соотношением сторон 3: 4: 5.

Золотое сечение (золотая пропорция) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон.

Математические знания египтян • В наше время математика древних египтян кажется довольно примитивной, ведь египтяне не пошли дальше арифметики дробей, уравнений первой степени и неполных квадратных уравнений. Однако, древний ученый шел непроторенными путями, и в круге тех понятий и проблем его ум работал не менее интенсивно, чем теперь ум математика над той или иной нерешенной современной задачей. • Основное внимание сконцентрировано не на методах решения задач, а на самих вычислениях и трудностях, которые встают перед решающим задачу.

Значение математики Древнего Египта В древнем Египте математика представляла собой совокупность знаний, ещё не разделившуюся на арифметику, алгебру, геометрию и выступающую, прежде всего, как собрание правил для численного решения простейших арифметических, алгебраических и геометрических задач. Проблемы, стоявшие перед египетскими чиновниками, были, главным образом, практические. Многие решения находили путём проб, ощупью, и не удивительно, что они оказывались иногда громоздкими и требовали преодоления больших трудностей. Но наряду с этим обобщались задачи, и они начинали принимать более абстрактных характер. При исследовании отдельных проблем вырабатывались приёмы геометрических и алгебраических преобразований, которые предвещали дальнейший рост этих составных частей математической дедукции.

Математика древнего Египта оказала несомненное влияние на последующие судьбы науки. Сами греки рассказывали, что многие начальные сведения приобретены ими во время поездок в Египет.