вероятность л 3.ppt
- Количество слайдов: 55
 Математика Теория вероятностей и элементы математической статистики Лекцию читает Ткаченко Геннадий Григорьевич кандидат физико-математический наук, доцент 1
Математика Теория вероятностей и элементы математической статистики Лекцию читает Ткаченко Геннадий Григорьевич кандидат физико-математический наук, доцент 1
 Формула полной вероятности Пример. Из 10 экзаменационных билетов студент считает 6 билетов "счастливыми". На экзамен он заходит вторым. Допустим, что второй студент не знает выбора первого. Найдем вероятность, что он выберет "счастливый" билет. 2 2
Формула полной вероятности Пример. Из 10 экзаменационных билетов студент считает 6 билетов "счастливыми". На экзамен он заходит вторым. Допустим, что второй студент не знает выбора первого. Найдем вероятность, что он выберет "счастливый" билет. 2 2
 A = {второй студент взял "счастливый" билет} H 0= {первый студент взял "несчастливый" билет} H 1= {первый студент взял "счастливый" билет} A = H 0 A+H 1 A p(A) = p(H 0 A)+p(H 1 A) Применим к каждому слагаемому теорему умножения p(AB) = p(A / B) p(B) Получаем формулу полной вероятности 3
A = {второй студент взял "счастливый" билет} H 0= {первый студент взял "несчастливый" билет} H 1= {первый студент взял "счастливый" билет} A = H 0 A+H 1 A p(A) = p(H 0 A)+p(H 1 A) Применим к каждому слагаемому теорему умножения p(AB) = p(A / B) p(B) Получаем формулу полной вероятности 3
 Самостоятельно вычислить полной вероятности по формуле 4
Самостоятельно вычислить полной вероятности по формуле 4
 Выводы Вероятности, что первый и второй студенты выбирают "счастливый" ("несчастливый") билеты равны 5
Выводы Вероятности, что первый и второй студенты выбирают "счастливый" ("несчастливый") билеты равны 5
 Последовательность независимых испытаний. Формула Бернулли. Пример Три раза подбрасывают кубик. Найдем вероятность, что шесть очков выпадет два раза. Обозначим A={при одном бросании выпало шесть очков} 6
Последовательность независимых испытаний. Формула Бернулли. Пример Три раза подбрасывают кубик. Найдем вероятность, что шесть очков выпадет два раза. Обозначим A={при одном бросании выпало шесть очков} 6
 Обозначим = {при трех бросаниях шесть очков выпало ровно 2 раза} 7
Обозначим = {при трех бросаниях шесть очков выпало ровно 2 раза} 7
 Последовательность из n испытаний образует схему Бернулли, если 1) испытания взаимно независимы т. е. их исходы независимы; 2) при каждом испытании событие A может произойти с постоянной вероятностью p Событие A называют "успехом" испытания, а противоположное событие - "неудачей". Обозначим вероятность"неудачи" q=1 -p. 8
Последовательность из n испытаний образует схему Бернулли, если 1) испытания взаимно независимы т. е. их исходы независимы; 2) при каждом испытании событие A может произойти с постоянной вероятностью p Событие A называют "успехом" испытания, а противоположное событие - "неудачей". Обозначим вероятность"неудачи" q=1 -p. 8
 обозначает событие, что в n испытаниях произошло ровно m "успехов" Для вероятности этого события справедлива формула Бернулли m = 0, 1, 2, …, n 9
обозначает событие, что в n испытаниях произошло ровно m "успехов" Для вероятности этого события справедлива формула Бернулли m = 0, 1, 2, …, n 9
 Пример Три раза подбрасывают кубик. Найдем вероятность, что шесть очков выпадет не более двух раз. "Успехом" испытания будем считать выпадение 6 очков. Вероятность "успеха" p=1/6 , вероятность "неудачи" q=5/6 10
Пример Три раза подбрасывают кубик. Найдем вероятность, что шесть очков выпадет не более двух раз. "Успехом" испытания будем считать выпадение 6 очков. Вероятность "успеха" p=1/6 , вероятность "неудачи" q=5/6 10
 Обозначим через C событие, что число шестерок не превосходит двух. Тогда событие можно представить в виде суммы несовместных событий 11
Обозначим через C событие, что число шестерок не превосходит двух. Тогда событие можно представить в виде суммы несовместных событий 11
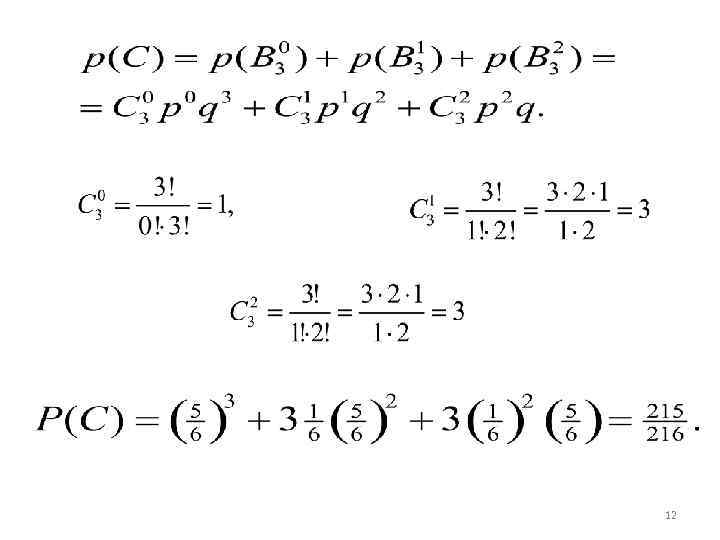 12
12
 Геометрическое определение вероятности Пример. Производится один выстрел по круглой мишени радиуса R. Предполагается, что каждая точка мишени может быть поражена с одинаковой вероятностью. Найти вероятность попадания в круг радиуса r (r
Геометрическое определение вероятности Пример. Производится один выстрел по круглой мишени радиуса R. Предполагается, что каждая точка мишени может быть поражена с одинаковой вероятностью. Найти вероятность попадания в круг радиуса r (r
 Тогда вероятность этого события по формуле будет равна Если множество равновероятных исходов – интервал [a, b] , то вероятность попадания в [c, d] равна 14
Тогда вероятность этого события по формуле будет равна Если множество равновероятных исходов – интервал [a, b] , то вероятность попадания в [c, d] равна 14
 Случайные величины Пример Обозначим буквой число гербов, выпавших при подбрасывании двух монет различного достоинства. Это число будет случайной величиной. 15
Случайные величины Пример Обозначим буквой число гербов, выпавших при подбрасывании двух монет различного достоинства. Это число будет случайной величиной. 15
 Найдем вероятности этих значений. Предположим, что монеты правильные: вероятности всех элементарных событий равны 1/4. Обозначим через Аi событие, что выпало i гербов. A 0 ={ЦЦ}, A 1= {ГЦ, ЦГ}, P(A 0)=1/4 , P(A 1)=2/4, A 2={ГГ} P(A 2)=1/4 16
Найдем вероятности этих значений. Предположим, что монеты правильные: вероятности всех элементарных событий равны 1/4. Обозначим через Аi событие, что выпало i гербов. A 0 ={ЦЦ}, A 1= {ГЦ, ЦГ}, P(A 0)=1/4 , P(A 1)=2/4, A 2={ГГ} P(A 2)=1/4 16
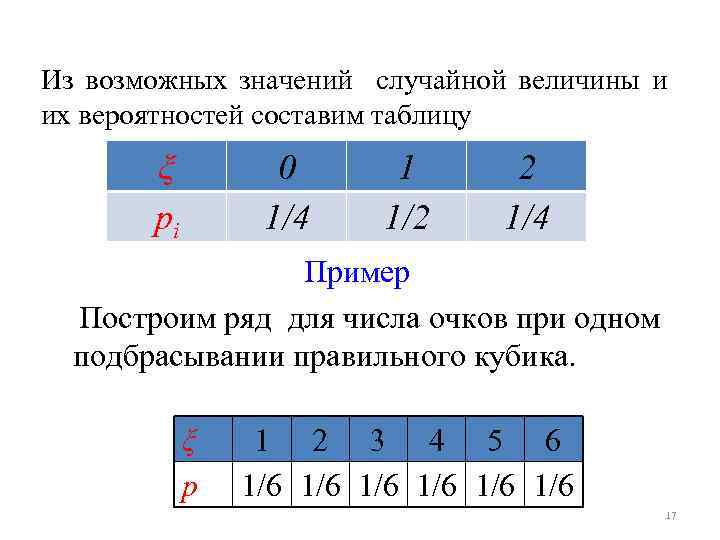 Из возможных значений случайной величины и их вероятностей составим таблицу ξ pi 0 1/4 1 1/2 2 1/4 Пример Построим ряд для числа очков при одном подбрасывании правильного кубика. ξ p 1 2 3 4 5 6 1/6 1/6 1/6 17
Из возможных значений случайной величины и их вероятностей составим таблицу ξ pi 0 1/4 1 1/2 2 1/4 Пример Построим ряд для числа очков при одном подбрасывании правильного кубика. ξ p 1 2 3 4 5 6 1/6 1/6 1/6 17
 Случайной величиной называется функция, которая каждому элементарному событию ставит в соответствие число. Эти числа называют возможными значениями случайной величины. Случайные величины будем обозначать греческими буквами , , , а их возможные значения – латинскими буквами с индексами x i , y i , zi. 18 18
Случайной величиной называется функция, которая каждому элементарному событию ставит в соответствие число. Эти числа называют возможными значениями случайной величины. Случайные величины будем обозначать греческими буквами , , , а их возможные значения – латинскими буквами с индексами x i , y i , zi. 18 18
 Случайную величину называют дискретной, если ее возможные значения образуют последовательность чисел. Возможные значения xi и их вероятности pi называют рядом распределения дискретной случайной величины : ξ x 1 x 2 … xn pi p 1 p 2 … pn pi , i=1, 2, 19
Случайную величину называют дискретной, если ее возможные значения образуют последовательность чисел. Возможные значения xi и их вероятности pi называют рядом распределения дискретной случайной величины : ξ x 1 x 2 … xn pi p 1 p 2 … pn pi , i=1, 2, 19
 Функция распределения F(x) случайной величины определяется равенством F (x)=P ξ x} для всех x. ∘ x Пример Построим функцию распределения для числа гербов при подбрасывании двух монет. 20 20
Функция распределения F(x) случайной величины определяется равенством F (x)=P ξ x} для всех x. ∘ x Пример Построим функцию распределения для числа гербов при подбрасывании двух монет. 20 20
 Ряд распределения ξ pi 0 1/4 1 1/2 2 1/4 Возможные значения разбивают всю числовую ось на интервалы (- , 0), [0, 1), [1, 2), [2, + ). На каждом интервале функция распределения - постоянна 21
Ряд распределения ξ pi 0 1/4 1 1/2 2 1/4 Возможные значения разбивают всю числовую ось на интервалы (- , 0), [0, 1), [1, 2), [2, + ). На каждом интервале функция распределения - постоянна 21
 При любом x из интервала (- , 0) F(x)=0 При любом x из интервала F(x)=1/4 При любом x из интервала 1 2 F(x)=3/4 При любом x из интервала 2 ∞ F(x)=1 22
При любом x из интервала (- , 0) F(x)=0 При любом x из интервала F(x)=1/4 При любом x из интервала 1 2 F(x)=3/4 При любом x из интервала 2 ∞ F(x)=1 22
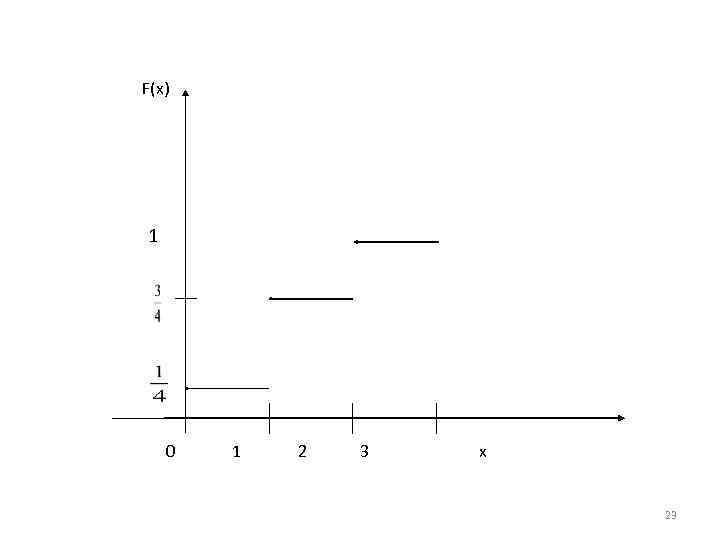 F(x) 1 0 1 2 3 x 23
F(x) 1 0 1 2 3 x 23
 Свойства функции распределения 1) При всех x 2) Функция распределения - неубывающая функция аргумента x F(x 1) F(x 2), если 3) Функция распределения непрерывна справа: F(x+0)=F(x). 24
Свойства функции распределения 1) При всех x 2) Функция распределения - неубывающая функция аргумента x F(x 1) F(x 2), если 3) Функция распределения непрерывна справа: F(x+0)=F(x). 24
![4) 5) Вероятность попадания случайной величины в интервал (a, b]. 25 4) 5) Вероятность попадания случайной величины в интервал (a, b]. 25](https://present5.com/presentation/-27667476_75067201/image-25.jpg) 4) 5) Вероятность попадания случайной величины в интервал (a, b]. 25
4) 5) Вероятность попадания случайной величины в интервал (a, b]. 25
 Пример Найдем вероятность, что число Г будет больше 1. . 26 26
Пример Найдем вероятность, что число Г будет больше 1. . 26 26
 Плотность распределения вероятностей случайной величины Случайная величина называется непрерывной, если множество ее возможных значений заполняют числовой интервал. Непрерывная случайная величина называется абсолютно непрерывной, если существует такая функция f(x), что Функция f(x) распределения величины . называется вероятностей плотностью случайной 27
Плотность распределения вероятностей случайной величины Случайная величина называется непрерывной, если множество ее возможных значений заполняют числовой интервал. Непрерывная случайная величина называется абсолютно непрерывной, если существует такая функция f(x), что Функция f(x) распределения величины . называется вероятностей плотностью случайной 27
 Равномерное распределение Пример Допустим, что интервал между автобусами составляет 10 минут. Пассажир не знает расписание автобуса. Время ожидания автобуса является любой величиной из [0, 10] с одинаковой вероятностью. F (x)=P ξ t} - вероятность, что время ожидания не больше t минут т. е. в интервале [0, t]. 28
Равномерное распределение Пример Допустим, что интервал между автобусами составляет 10 минут. Пассажир не знает расписание автобуса. Время ожидания автобуса является любой величиной из [0, 10] с одинаковой вероятностью. F (x)=P ξ t} - вероятность, что время ожидания не больше t минут т. е. в интервале [0, t]. 28
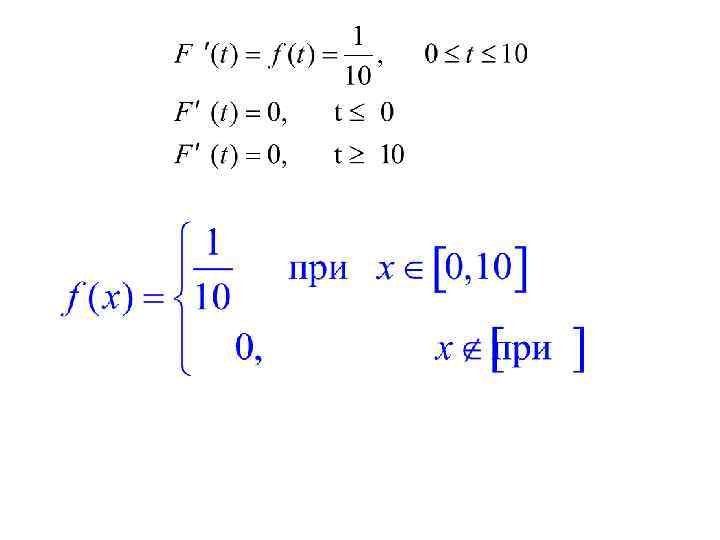
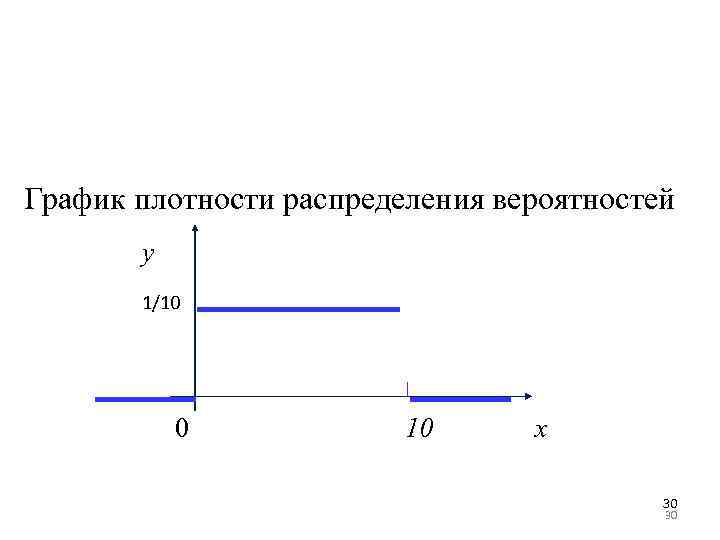 График плотности распределения вероятностей y 1/10 0 10 x 30 30
График плотности распределения вероятностей y 1/10 0 10 x 30 30
![Случайная величина ξ распределена равномерно на промежутке [a, b], если ее плотность распределения вероятностей Случайная величина ξ распределена равномерно на промежутке [a, b], если ее плотность распределения вероятностей](https://present5.com/presentation/-27667476_75067201/image-31.jpg) Случайная величина ξ распределена равномерно на промежутке [a, b], если ее плотность распределения вероятностей задается равенством 3131
Случайная величина ξ распределена равномерно на промежутке [a, b], если ее плотность распределения вероятностей задается равенством 3131
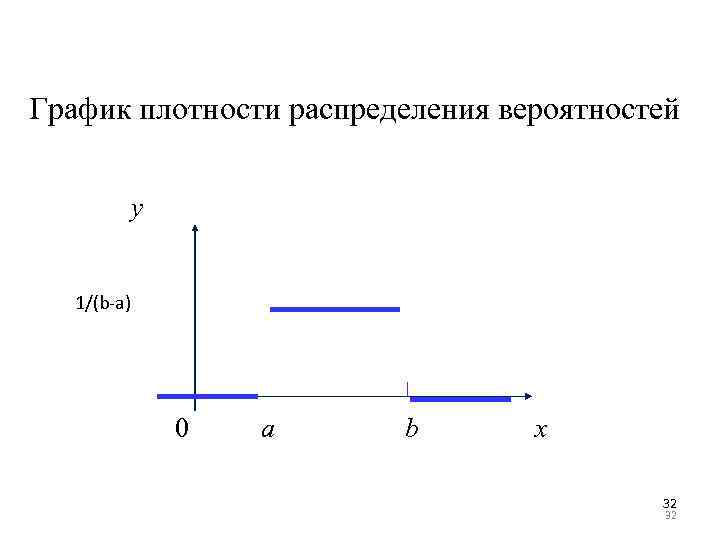 График плотности распределения вероятностей y 1/(b-a) 0 a b x 32 32
График плотности распределения вероятностей y 1/(b-a) 0 a b x 32 32
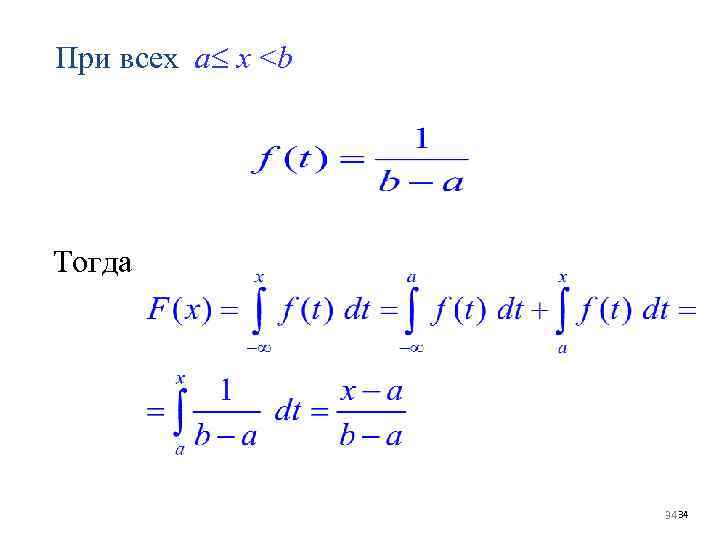 При всех a x
При всех a x
 35
35
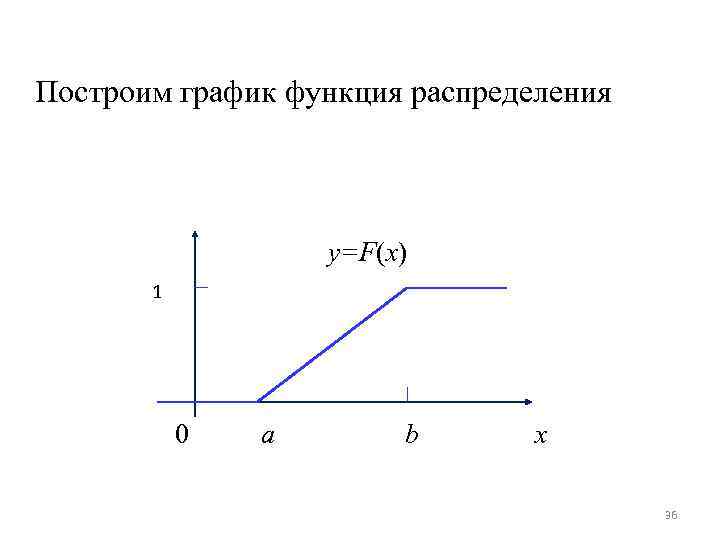 Построим график функция распределения y=F(x) 1 0 a b x 36
Построим график функция распределения y=F(x) 1 0 a b x 36
 Свойства плотности распределения вероятностей 1) В точках x непрерывности f (x) имеет место равенство 2) Для всех x плотность распределения вероятностей неотрицательна 37
Свойства плотности распределения вероятностей 1) В точках x непрерывности f (x) имеет место равенство 2) Для всех x плотность распределения вероятностей неотрицательна 37
 3) Свойство нормировки 4) Вероятности попадания случайной величины в следующие интервалы равны: 38
3) Свойство нормировки 4) Вероятности попадания случайной величины в следующие интервалы равны: 38
 Пример. Найдем вероятность, что время ожидания автобуса будет от 2 до 5 минут т. е. в интервале [2, 5] 39 39
Пример. Найдем вероятность, что время ожидания автобуса будет от 2 до 5 минут т. е. в интервале [2, 5] 39 39
 Пары случайных величин Пример Подбрасывают достоинства. две монеты различного Случайная величина ξ принимает значение 1, если первый раз выпадает Г, и 0, если выпадает Ц. Случайная величина η принимает значение 1, если второй раз выпадает Г, и 0, если выпадает Ц. 40
Пары случайных величин Пример Подбрасывают достоинства. две монеты различного Случайная величина ξ принимает значение 1, если первый раз выпадает Г, и 0, если выпадает Ц. Случайная величина η принимает значение 1, если второй раз выпадает Г, и 0, если выпадает Ц. 40
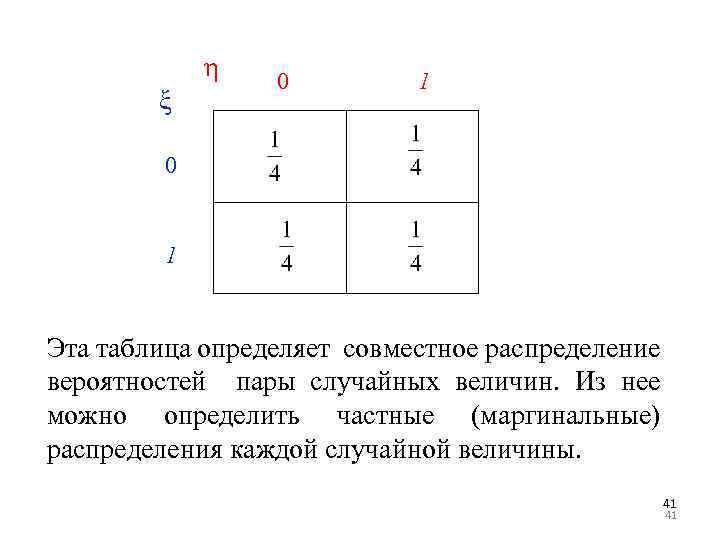 η ξ 0 1 Эта таблица определяет совместное распределение вероятностей пары случайных величин. Из нее можно определить частные (маргинальные) распределения каждой случайной величины. 41 41
η ξ 0 1 Эта таблица определяет совместное распределение вероятностей пары случайных величин. Из нее можно определить частные (маргинальные) распределения каждой случайной величины. 41 41
 Вероятность, что случайная величина ξ примет значение 0 будет равна т. е. сумма первой строки. Вероятность, что случайная величина ξ примет значение 1 будет равна т. е. сумма второй строки. 42 42
Вероятность, что случайная величина ξ примет значение 0 будет равна т. е. сумма первой строки. Вероятность, что случайная величина ξ примет значение 1 будет равна т. е. сумма второй строки. 42 42
 Суммы первого и второго столбцов дают частные распределения второй случайной величины
Суммы первого и второго столбцов дают частные распределения второй случайной величины
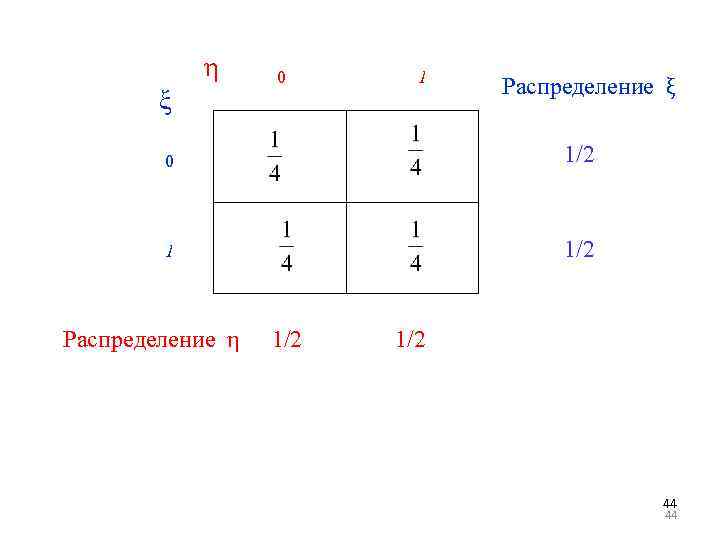 η ξ 0 1 Распределение ξ 0 1/2 1 1/2 Распределение η 1/2 44 44
η ξ 0 1 Распределение ξ 0 1/2 1 1/2 Распределение η 1/2 44 44
 Пример Допустим, что два студента последовательно друг за другом выбирают по одному лотерейному билету. Лотерея состоит из 10 билетов, среди которых 6 билетов выигрышных. Пусть случайная величина ξ принимает значение V, если первый студент выбрал выигрышный билет, и 0 в противном случае. Случайная величина η принимает значение V, если второй студент выбрал выигрышный билет, и 0 в противном случае. 45 45
Пример Допустим, что два студента последовательно друг за другом выбирают по одному лотерейному билету. Лотерея состоит из 10 билетов, среди которых 6 билетов выигрышных. Пусть случайная величина ξ принимает значение V, если первый студент выбрал выигрышный билет, и 0 в противном случае. Случайная величина η принимает значение V, если второй студент выбрал выигрышный билет, и 0 в противном случае. 45 45
 Пара случайных величин (ξ, η) принимает возможные значения (0, 0) (0, V) (V, 0) (V, V) Найдем вероятности каждой пары. Обозначим A = {первый студент взял выигрышный билет} = {первый студент взял невыигрышный билет} B = {второй студент взял выигрышный билет} = {второй студент взял невыигрышный билет} 46 46
Пара случайных величин (ξ, η) принимает возможные значения (0, 0) (0, V) (V, 0) (V, V) Найдем вероятности каждой пары. Обозначим A = {первый студент взял выигрышный билет} = {первый студент взял невыигрышный билет} B = {второй студент взял выигрышный билет} = {второй студент взял невыигрышный билет} 46 46
 Пара случайных величин принимает значение (0, 0), если оба студента выбирают невыигрышные билеты т. е. произойдет произведение событий По формуле умножения Пара случайных величин принимает значение (0, V) будет выбрана, если первый студент выбирает невыигрышный билет, а второй - выигрышный билет - т. е. произойдет произведение событий 47 47
Пара случайных величин принимает значение (0, 0), если оба студента выбирают невыигрышные билеты т. е. произойдет произведение событий По формуле умножения Пара случайных величин принимает значение (0, V) будет выбрана, если первый студент выбирает невыигрышный билет, а второй - выигрышный билет - т. е. произойдет произведение событий 47 47
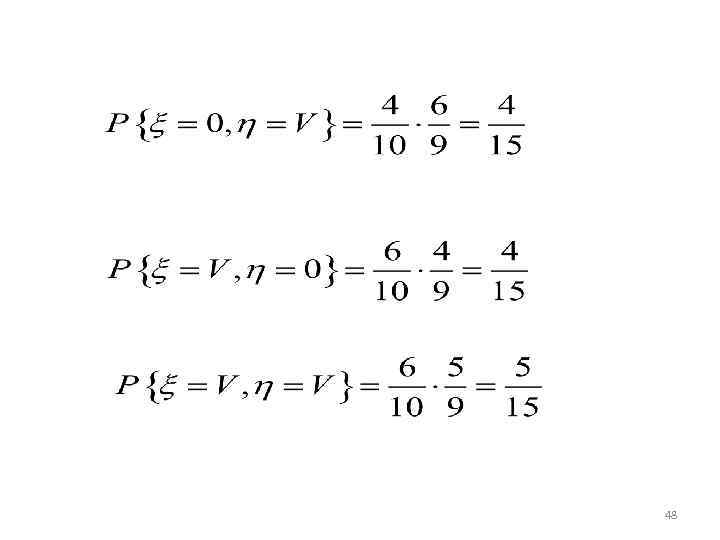 48
48
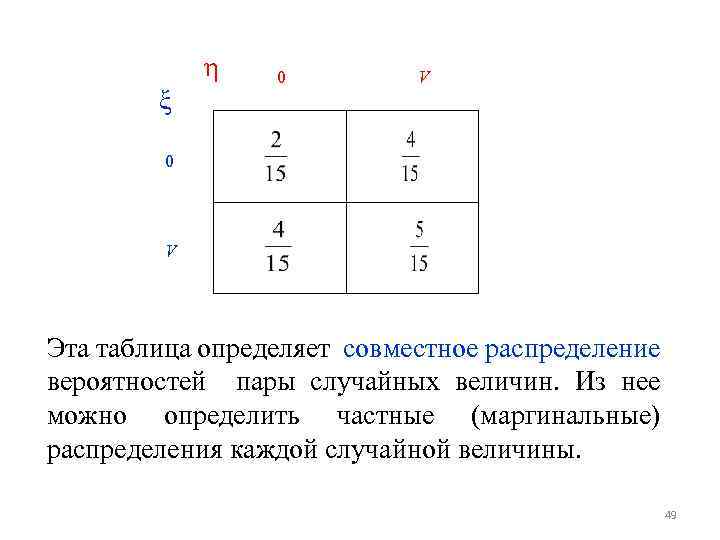 η ξ 0 V Эта таблица определяет совместное распределение вероятностей пары случайных величин. Из нее можно определить частные (маргинальные) распределения каждой случайной величины. 49
η ξ 0 V Эта таблица определяет совместное распределение вероятностей пары случайных величин. Из нее можно определить частные (маргинальные) распределения каждой случайной величины. 49
 Вероятность, что случайная величина ξ примет значение 0 т. е. первый студент получит невыигрышный билет будет равна т. е. сумма первой строки. Вероятность, что случайная величина ξ примет значение V равна сумме второй строки. 50
Вероятность, что случайная величина ξ примет значение 0 т. е. первый студент получит невыигрышный билет будет равна т. е. сумма первой строки. Вероятность, что случайная величина ξ примет значение V равна сумме второй строки. 50
 Суммы первого и второго столбцов дают частные распределения второй случайной величины η 0 1 Распределение ξ ξ 2/5 0 1 Распределение η 3/5 2/5 3/5 51
Суммы первого и второго столбцов дают частные распределения второй случайной величины η 0 1 Распределение ξ ξ 2/5 0 1 Распределение η 3/5 2/5 3/5 51
 Пусть первая случайная величина ξ принимает значения x 1, x 2, …, xn, вторая случайная величина η принимает значения y 1, y 2, …, ym, Обозначим через pij вероятность, что пара случайных величин принимает значение вектора (xi, yj): pij≥ 0 52
Пусть первая случайная величина ξ принимает значения x 1, x 2, …, xn, вторая случайная величина η принимает значения y 1, y 2, …, ym, Обозначим через pij вероятность, что пара случайных величин принимает значение вектора (xi, yj): pij≥ 0 52
 Вероятности pij задают совместное распределение вероятностей пары случайных величин: y 1 p 11 … … … xi . pi 1 xn pn 1 x 1. yj p 1 j ym p 1 m pij . pim pnj pnm Из таблицы можно определить частные (маргинальные) распределения каждой случайной величины: 53
Вероятности pij задают совместное распределение вероятностей пары случайных величин: y 1 p 11 … … … xi . pi 1 xn pn 1 x 1. yj p 1 j ym p 1 m pij . pim pnj pnm Из таблицы можно определить частные (маргинальные) распределения каждой случайной величины: 53
 Совместной функцией распределения случайных величин называется функция пары 54
Совместной функцией распределения случайных величин называется функция пары 54
 Функции задают частные (маргинальные) распределения каждой случайной величины ξ и η. Случайные величины ξ и η называются независимыми, если независимы события Для того, чтобы случайные величины ξ и η были независимы, необходимо и достаточно 55
Функции задают частные (маргинальные) распределения каждой случайной величины ξ и η. Случайные величины ξ и η называются независимыми, если независимы события Для того, чтобы случайные величины ξ и η были независимы, необходимо и достаточно 55



