Математика Предмет и метод математики Место в системе

Математика Предмет и метод математики. Место в системе наук

Предмет математики • Математика изучает действительный, материальный мир, объекты этого мира и отношения между ними, взятые в отвлечении от их содержания. • Специфика математики: выделение количественных отношений и пространственных форм, присущих всем предметам и явлениям, независимо от их вещественного содержания. Ф Энгельс: «Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть — весьма реальный материал. … Но чтобы быть в состоянии исследовать эти формы и отношения в чистом виде, необходимо совершенно отделить их от их содержания, оставить это последнее в стороне, как нечто безразличное…»

Модель, оригинал, структурная модель • Модель –сложный объект, определенным элементам которого можно поставить в соответствие элементы другого сложного объекта — оригинала; при этом взаимосвязям и отношениям между элементами оригинала соответствуют некоторые взаимосвязи или отношения между определенными элементами модели. • Структурная модель системы – модель, отражающая только структуру, только схему отношений между элементами системы Математики фактически имеет дело со структурными моделями исследуемых объектов

ХАРАКТЕРНЫЕ ЧЕРТЫ МАТЕМАТИКИ • • • Математика изучает абстрагированные свойства предметов. При этом математика абсолютизирует свои абстракции: возникшие в ходе ее развития математические понятия в дальнейшем закрепляются и рассматриваются как данные. Сравнение результатов, полученных в математике, с реальной действительностью является задачей не столько математики, сколько ее приложений. Основным методом получения математических результатов является логический вывод, не опирающийся на экспериментальную проверку. Если приняты исходные посылки, то полученные из них математическим путем результаты непреложны. Если же результаты расходятся с опытом, то следует подвергнуть исследованию принятые посылки. Абстракции, возникающие в математике, развиваются ступенчато — от абстракций, непосредственно обобщающих свойства реальных предметов, к абстракциям высокого уровня. . Математика обладает свойством универсальной применимости. В любой области, где только удается математически поставить задачу, математика дает результат с точностью, соответствующей точности постановки задачи. Математика занимает особое положение в системе наук. Она дает те основные понятия, которые используются в других науках (фундаментальные знания).

Математическое моделирование • Математическая модель — это приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Объект Модель Математическая модель Другие объекты Математика исходит из практики, создавая математические модели явлений, и возвращается к ней, показывая возможность применения результатов, полученных на основе изучения этих моделей.

Абстрактная структура Задание абстрактной структуры: • определение элементов структуры; • определение взаимных отношений элементов структуры; • определение основных правил, которым подчиняются элементы структуры (аксиом)

АКСИОМАТИЧЕСКИЙ МЕТОД В МАТЕМАТИКЕ Аксиоматический метод : • некоторые понятия и связывающие их отношения считаются неопределяемыми, исходными, а все дальнейшие понятия и их свойства выводят из исходных путем точных определений и логических рассуждений. Аксиоматический метод - один из основных методов построения математических моделей действительности

Примеры абстрактных структур Система чисел: • • Элементы – числа Отношения между элементами – отношения сравнения (x<=y) Действия – система арифметических действий Система правил – аксиомы алгебры чисел N = {1, 2, 3, …} – натуральный ряд чисел; Z ={-…-3, -2, -1, 0, 1, 2, 3, …} – ряд целых чисел; Q = {Zi/Zj } – ряд рациональных чисел; R={Q+I} – ряд действительных чисел; C – ряд комплексных чисел.

Примеры абстрактных структур Система геометрических объектов (геометрия Евклида): • Система начальных понятий (- «точка – объект без длины, ширины и толщины» , - «линия - объект без ширины и толщины» , - «поверхность - объект без толщины» …) • Система постулатов (9 постулатов) • Система аксиом – утверждений, принимаемых без доказательства (5 аксиом) – ( «через 2 точки можно провести только 1 прямую» – «через одну точку нельзя провести более одно прямой, параллельной данной» ; …) • Система теорем – утверждений, выводимых из аксиом и определений путем логических рассуждений (- «если 3 стороны одного треугольника равны 3 сторонам другого, то такие треугольники равны» …)

Примеры абстрактных структур Алгебра высказываний (математическая логика): • Элементы – высказывания • Система действий над высказываниями – логические действия • Система правил – аксиомы алгебры высказываний Высказывание – предложение, относительно которого можно сказать, истинно оно или ложно. Может иметь значения: 1 (True или Истина) или 0 (False или Ложь) Пример: [A]=1 – высказывание А истинно; [A]=0 – высказывание А ложно

Система действий над высказываниями Результат действий над высказываниями – новое высказывание, имеющее значение 0 или 1. • Логические действия: – – – Инверсия ‾ (логическое НЕ); Конъюнкция (логическое И) ; Дизъюнкция (логическое ИЛИ); Следование (Импликация, ЕСЛИ…То); Эквиваленция (ТОГДА И ТОЛЬКО ТОГДА);

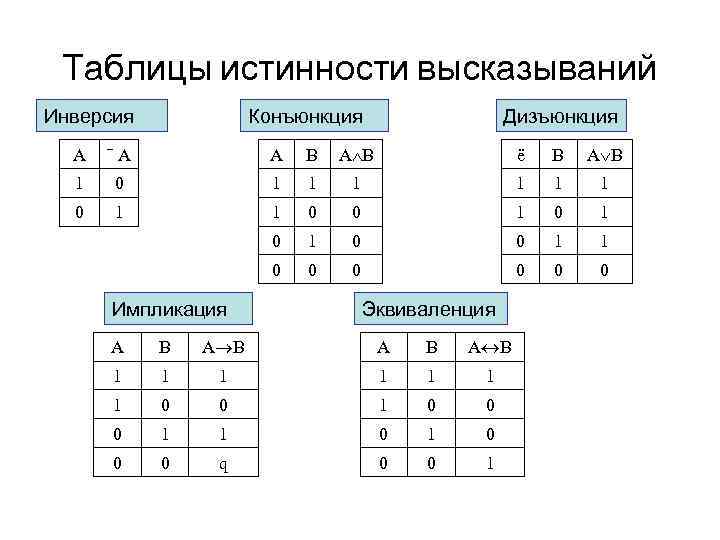Таблицы истинности высказываний Инверсия Конъюнкция Дизъюнкция A ‾A A B ё B A B 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 0 Импликация Эквиваленция A B A B 1 1 1 1 0 0 0 q 0 0 1

Система действий над высказываниями Логическая формула – сложное высказывание, составленное из простых высказываний, соединенных логическими действиями. Имеет значение 0 или 1 Пример: (А B)→C; (А B) (А B) Противоречие - логическая формула, принимающая значение 0 при любых значениях составляющих ее высказываний Тавтология - логическая формула, принимающая значение 1 при любых значениях составляющих ее высказываний Предикат - логическое предложение, содержащее переменные, принимающая конкретное значение (1 или 0) при подстановке значений составляющих ее переменных Пример: x > 5; (А x)

Аксиомы алгебры высказываний • Двойное отрицание ⌐(⌐A)=А • Коммутативность: A B=B A A B = B A; • Ассоциативность: A (B D) = (A B) D A (B D) = (A B) D • Дистрибутивность: A (B D) = (A B) (A D) • Закон идемпотентности: A А =A A А =A • Закон поглощения: A (A B) =А A (A B) = А • Законы Моргана: ⌐(A B) = ⌐(A) ⌐(B) A В= ⌐(A) B A В=(A В) ( B A)

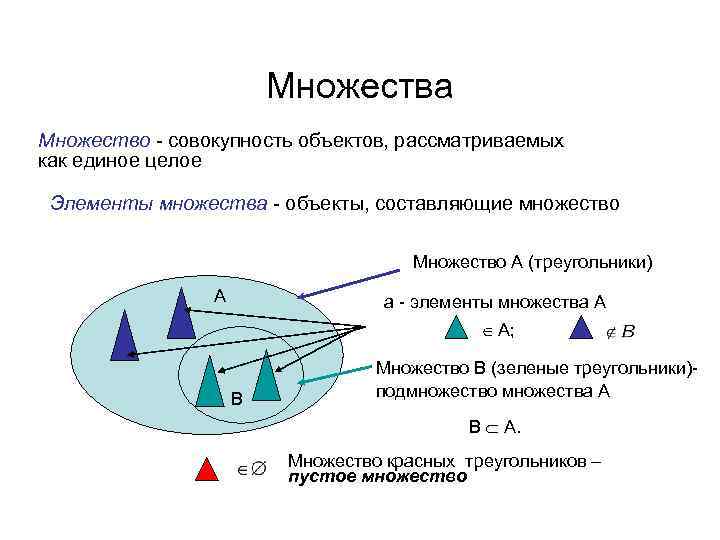Множества Множество - совокупность объектов, рассматриваемых как единое целое Элементы множества - объекты, составляющие множество Множество А (треугольники) А а - элементы множества А A; В Множество В (зеленые треугольники)подмножество множества А B A. Множество красных треугольников – пустое множество

Способы задания множеств • Перечисление элементов множества: • A={1, 2, 3} • Описанием общего свойства элементов • Задание по имени: (N - натуральные, Z – целые, Q – рациональные, R – действительные, C – комплексные) • С помощью порождающей процедуры

Операции над множествами • Объединение: • Пересечение: • Разность • Дополнение • Декартово произведение множеств А и В Или С(А)

Аксиомы теории множеств • Коммутативность: A B=B A A B = B A • Ассоциативность: A (B D) = (A B) D A (B D) = (A B) D • Дистрибутивность: A (B D) = (A B) (A D) • Закон идемпотентности: A А =A A А =A • Закон поглощения: A (A B) =А A (A B) = А • Законы Моргана: С(A B) = С(A) С(B) • Законы пустого и универсального множеств A =A; A U=A A C(A)=U; A C(A)= A U=U; A =

Отношения между множествами • Отношение равенства: Множества А и В равны, если каждый элемент А является элементом В и наоборот. x x B x A • Отношение включения: Если каждый элемент множества B является также и элементом множества A, то множество B является подмножеством множества А. B A. x x B → x A • Сравнение множеств: Мощность множества – количество элементов множества Множества А и В равномощны, если существует взаимно-однозначное соответствие между элементами множеств А и В

Бинарные отношения • Бинарное отношение – подмножество ρ упорядоченных пар (а, b) декартова произведения множеств А и В, обладающих определенным общим свойством: Элемент a множества А находится в бинарном отношении ρ с элементом b множества В: (a, b) ρ или a ρ b Способы задания отношений: - перечисление всех пар элементов, находящихся в отношении ρ: Для А={1, 2, 3}; B={1, 3, 5} ρ={(1, 1), (3, 3)} – отношение «одинаковые элементы множеств А и В» -задание характеристического свойства пар: Для действительных чисел x, y R x = y - отношения равенства, x y – отношение сравнения по величине Для множества прямых a и b в пространстве а b – отношения параллельности, а b - отношения перпендикулярности

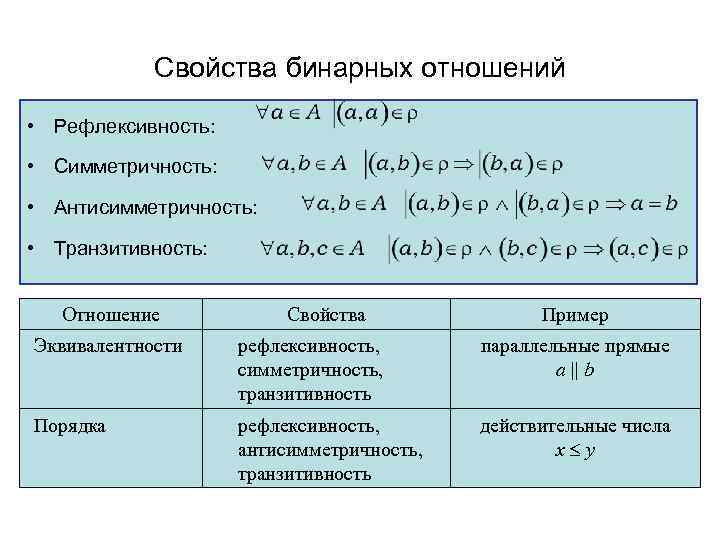Свойства бинарных отношений • Рефлексивность: • Симметричность: • Антисимметричность: • Транзитивность: Отношение Свойства Пример Эквивалентности рефлексивность, симметричность, транзитивность параллельные прямые а || b Порядка рефлексивность, антисимметричность, транзитивность действительные числа x y

Классы эквивалентности • Классы эквивалентности – подмножества А 1, А 2, …, для которых внутри каждого подмножества элементы состоят в отношении эквивалентности, а элементы разных подмножеств – не состоят. А = А 1 А 2; А 1 А 2 = Классификация или разбиением множества на классы представление этого множества в виде объединения непустых попарно непересекающихся своих подмножеств Если n – число свойств, то максимальное число классов в разбиении равно 2 n.

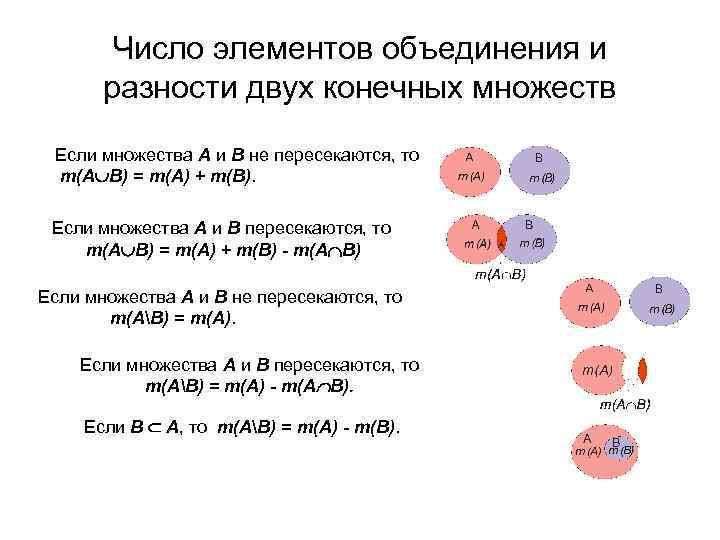Число элементов объединения и разности двух конечных множеств Если множества A и B не пересекаются, то m(A B) = m(A) + m(B). Если множества A и B пересекаются, то m(A B) = m(A) + m(B) - m(A B) Если множества A и B не пересекаются, то m(AB) = m(A). Если множества A и B пересекаются, то m(AB) = m(A) - m(A B). Если В А, то m(AB) = m(A) - m(B).

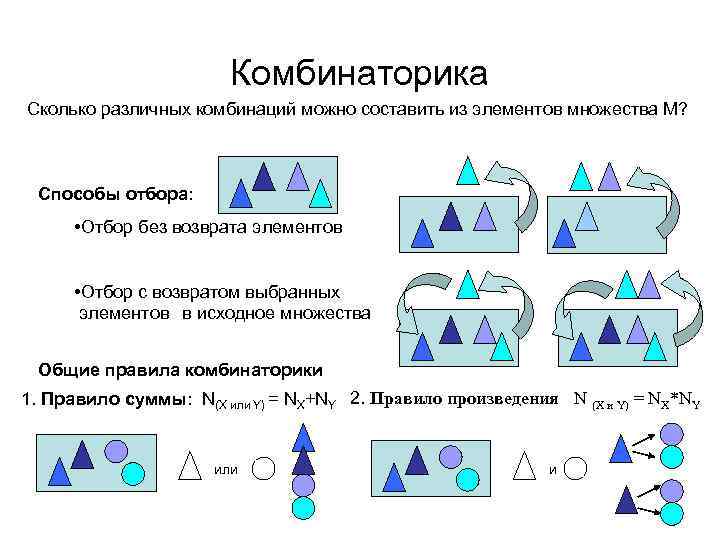Комбинаторика Сколько различных комбинаций можно составить из элементов множества М? Способы отбора: • Отбор без возврата элементов • Отбор с возвратом выбранных элементов в исходное множества Общие правила комбинаторики 1. Правило суммы: N(X или Y) = NX+NY 2. Правило произведения N (X и Y) = NX*NY или и

Перестановки • Дано: множество из n элементов: E={a 1, a 2, … an} Задача: выбрать все элементы множества E и переставить их всеми возможными способами. Перестановки из n различных элементов – все возможные последовательности этих n элементов. Порядок элементов имеет значение! • Без повторения элементов: 1 2 3 4 • С повторяющимися элементами:

Размещения Задача: выбрать часть элементов множества E и переставить их всеми возможными способами. Размещения из n различных элементов по m элементов – упорядоченные последовательности m различных элементов, выбранных из исходных n, которые отличающиеся или порядком следования элементов, или составом элементов. • Без повторения элементов: 1 2 • С повторяющимися элементами: 1 2

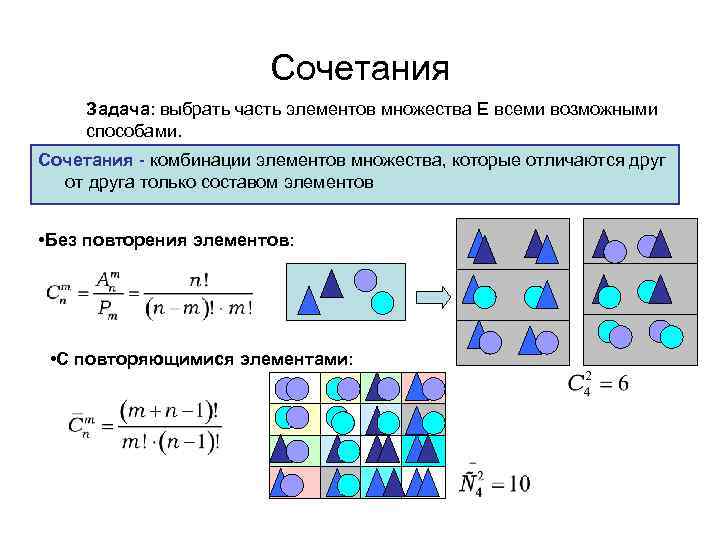Сочетания Задача: выбрать часть элементов множества E всеми возможными способами. Сочетания - комбинации элементов множества, которые отличаются друг от друга только составом элементов • Без повторения элементов: • С повторяющимися элементами: