MATEMATIKA Postoji piramida znanosti a osnovicu te piramide

MATEMATIKA Postoji piramida znanosti, a osnovicu te piramide čini matematika jer se jedino ona ne oslanja ni na jednu drugu znanost. Pritom još svima služi! Kaže se zato da je matematika i boginja i robinja.

No, mnogi se uozbilje već i na sam spomen njezina imena. Pokažimo djeci da matematika može biti i jedna velika zabava. Čitava jedna njezina grana svoje korijene vuče iz zagonetki, igara i problema za razbibrigu. Želja mi je da se danas zabavite dok zajedno sa mnom prolazite kroz taj svijet.

KOMBINATORIKA I VJEROJATNOST U SVAKODNEVNICI 02. 12. 2010. Pripremila: doc. dr. sc. Snježana BraićPrirodoslovno , matematički fakultet , Split sbraic@pmfst. hr

Uvod Za početak teorije vjerojatnosti uzima se 1654. godina kada se pariški građanin De Mere obratio slavnim matematičarima tog vremena Pascalu i Fermatu sa sljedećim problemom: Je li preporučljivokladitise da će u 24 uzastopna bacanja dviju različitih igraćihkocaka barem jednom pasti dvije šestice? Bio je to pokušaj da se predvidi određena situacija u kojoj je prisutna neizvjesnost njezina ishoda.

Općenito se teorija vjerojatnosti prirodno povezivala s predskazivanjem budućnosti, pa je vjerojatnost kroz povijest bila predmetom mnogih spekulacija i različitih interpretacija. Stoga je bio dug put od njezinog intuitivnog poimanja do današnjeg, precizno i strogo utemeljenog područja matematike.

U mnogim istraživanjima provode se različiti pokusi (eksperimenti). Ti pokusi mogu biti determinirani ili slučajni, a teorija vjerojatnosti se bavi slučajnim pokusima. Slučajanpokus je pokus čiji ishod nije jednoznačno određen uvjetima u kojima se taj pokus izvodi, pa nismo u stanje točno predvidjeti kada će nastupiti neki događaj. Teorija vjerojatnosti formira i proučava matematičke modele slučajnih pokusa.

Osnovni polazni objekt u teoriji vjerojatnosti je skup svih mogućih ishoda nekog slučajnog pokusa. Taj skup nazivamo prostorom elementarnihdogađajai označavamo s Ω. Npr. bacanje novčića je pokus kod kojeg je svaki ishod element dvočlanog skupa {P, G}, dok je kod bacanja jedne igraće kocke prostor elementarnih događaja skup {1, 2, 3, 4, 5, 6}.

Događaj A je svaki podskup prostora elementarnih događaja Ω. Npr. ako je slučajni pokus bacanje igraće kocke i ako događaj A glasi: “Pao je paran broj ", onda je A={2, 4, 6}. Svaki pojedini mogući ishod pokusa, tj. svaki element skupa Ω, nazivamo elementarnim događajem dok , događaj koji opisujemo pomoću više elementarnih događaja nazivamo složenim događajem. Svaki element skupa A nazivamo elementarnim događajem povoljnim za događaj A.

Na primjer, u slučajnom pokusu bacanja dviju različitih igraćih kocaka ustanoviti da se dogodio događaj “Suma brojeva koje smo dobili je jednaka 8" isto je što i ustanoviti da je pokus dao jedan od ishoda: (2, 6), (3, 5), (4, 4), (5, 3) ili (6, 2) (od 36 mogućih ishoda). Gornji događaj je, dakle, jedan složeni događaj sastavljen od 5 elementarnih događaja i za tih 5 elementarnih događaja kažemo da su povoljni za događaj A.

Cijeli prostor Ω nazivamo sigurnim događajem a , prazan skup nemogućim događajem(događaj koji se nikada neće dogoditi). Na primjer, pri bacanju dviju kocaka siguran događaj je da će zbrojeva koji padnu na tim kockama biti paran ili neparan broj, dok je nemoguć događaj da zbrojeva na tim kockama bude veći od 12.

Pogledajmo primjere kada i kako u svakodnevnom životu opisujemo vjerojatnosti nekog događaja. Idući tjedan ću _____ ići na more, a moj brat sigurno neće. vjerojatno ______ Vladimir je poznati lažljivac! Od njega je ________ gotovo nemoguće čuti istinu. Sutra Mirjana i Kristina u isto vrijeme slave rođendan. Ne znam još kojoj ću otići - ___________ vjerojatnost je pola-pola. Nisam učio zemljopis, a danas pišemo kontrolni. Nema šanse _____ da dobijem 5 ! Prošli sat sam odgovarala povijest, pa je gotovo sigurno da me ______ danas neće pitati. Uočimo izraze koje koristimo za opisivanje vjerojatnosti događaja!

Što je vjerojatnost nekog događaja i kako je računamo?

Intuitivna predodžba vjerojatnosti je vrlo jasna. Ako biste nekog na ulici upitali kolika je vjerojatnost da će pri bacanju novčića pasti pismo ili da će igraća kocka pokazati broj 5, većina bi bez razmišljanja odgovorila 1/2, odnosno 1/6, mada (vjerojatno ) ne znaju precizno izreći definiciju vjerojatnosti. No, pod vjerojatnošću intuitivno podrazumijevaju broj koji iskazuje omjer povoljnih ishoda i svih mogućih ishoda prilikom jednog vršenja pokusa.

Primjer 1. U vrećici se nalaze dvije crvene kuglice. Josip iz te vrećice izvlači jednu kuglicu. a) Kolika je vjerojatnost da će izvući plavu kuglicu? Nema ne može dogoditi! To 0 se šanse! % b) Kolika je vjerojatnost da će izvući crvenu kuglicu? To će se sigurno dogoditi! 100 %

Primjer 2. U vrećici se nalazi jedna crvena i jedna plava kuglica. Što je vjerojatnije: da Josip izvuče plavu ili da izvuče crvenu kuglicu ? Ta su dva događaja jednako vjerojatna i vjerojatnost tih događaja je 1/2.

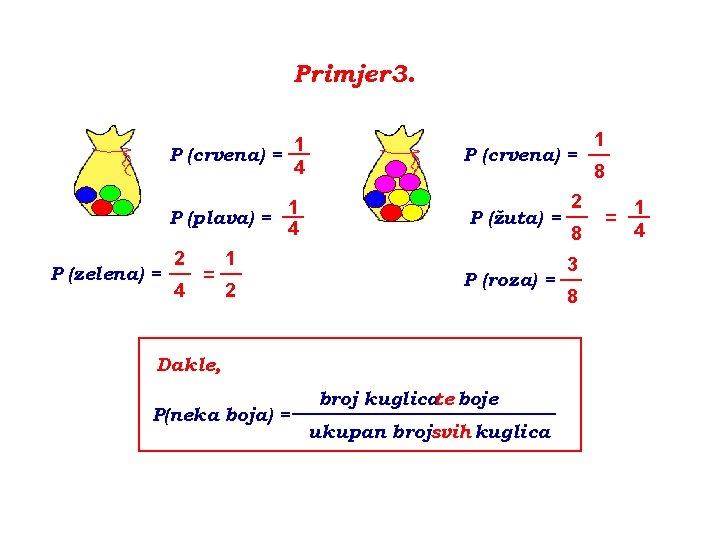Primjer 3. __ 1 P (crvena) = 4 P (plava) = 2 1 __ __ P (zelena) = = 4 2 __ 1 4 1 __ P (crvena) = 8 P (žuta) = 2 __ 1 __ = 4 8 3 __ P (roza) = 8 Dakle, broj kuglica boje te _____________ P(neka boja) = ukupan brojsvih kuglica

Općenito, ako je prostor elementarnih događaja Ω konačan skup i ako su svi elementarni događaji jednako vjerojatni, onda se vjerojatnost nekog događaja A Ω računa kao P(A) = broj elementarnih događaja povoljnihza A _____________________ ukupan brojsvih elementarnih događaja = A Ω

Iz toga slijedi da sigurandogađaj ima vjerojatnost 100 % = 1, napolavjerojatandogađaj ima vjerojatnost nemoguć događaj ima vjerojatnost 0 % = 0. 1 50 % = __, 2 Vjerojatnostnekog događaja je broj izmeđui 1. 0 Vjerojatnost 1 opisuje sigurandogađaj. Vjerojatnost 0 opisuje nemoguć događaj. Vjerojatnost 0. 5 opisuje napola vjerojatan događaj. Ostali brojevi između i 1 opisuju ostale manje ili više 0 vjerojatnedogađaje.

Povežimo i ostale izraze iz svakodnevnog života s brojevima koji opisuju vjerojatnost događaja ? 1 nemoguće sigurno malo vjerojatno vrlo vjerojatno pola - pola ? ? 0. 5 gotovo nemoguće gotovo sigurno ? vjerojatno ? ? 0 v j e r o j a t n o s t

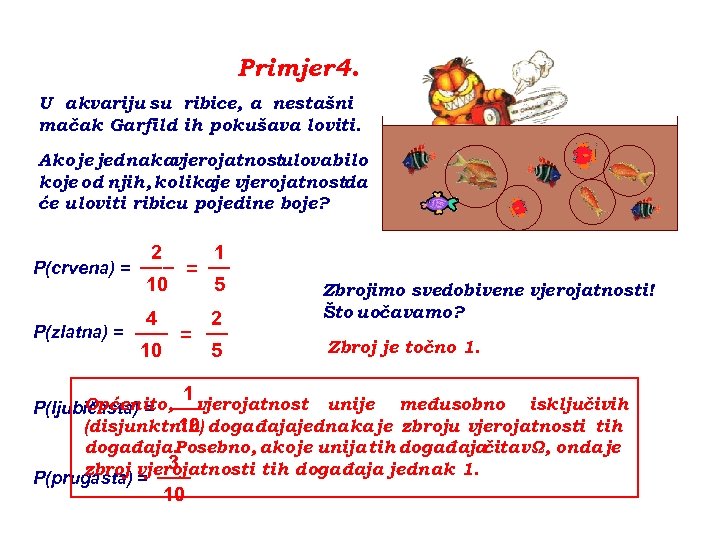Primjer 4. U akvariju su ribice, a nestašni mačak Garfild ih pokušava loviti. Ako je jednakavjerojatnost ulova bilo koje od njih, kolikaje vjerojatnostda će uloviti ribicu pojedine boje? 2 1 ___ __ P(crvena) = = 10 5 4 2 P(zlatna) = ___ = __ 10 5 1 Zbrojimo svedobivene vjerojatnosti! Što uočavamo? Zbroj je točno 1. Općenito, vjerojatnost unije međusobno isključivih P(ljubičasta) = ___ (disjunktnih) događajajednaka je zbroju vjerojatnosti tih 10 događaja. Posebno, ako je unija tih događaja čitavΩ, onda je 3 zbroj vjerojatnosti tih događaja jednak 1. ___ P(prugasta) = 10

Iz ovog odmah slijedi da je Stoga, ako želimo izračunati vjerojatnost da ne ulovimo npr. crvenu ribicu, ne moramo izbrojiti sve one ribice koje nisu crvene, već je dovoljno izračunati vjerojatnost da je ribica crvena (izbrojiti samo crvene ribice), a tražena vjerojatnost je tada P(ne crvena) =1 - P(crvene)

Vidjeli smo da ako je prostor elementarnih događaja Ω konačan, izračunati vjerojatnost nekog događaja A Ω znači odrediti koliko elemenata ima skup Ω (skup svih mogućih ishoda), a koliko skup A (skup povoljnih ishoda za događaj A). U svim našim primjerima bilo je lako izbrojiti koliko elemenata imaju ti skupovi. No, općenito problem prebrojanja elemenata konačnog skupa nije niti malo jednostavan.

Kombinatorika-matematička disciplina koja se bavi prebrajanjem elemenata konačnih skupova i njihovih podskupova. Naziv potječe od Leibniza(1666).

Već i manji skupovi mogu nam zadati probleme ako se elementi skupa na neki način grupiraju, a mi trebamo izbrojiti koliko ima takvih grupa. Tada brojanje može biti prava vještina. Na primjer, na koliko načina možemo između 10 ljudi odabrati trojicu? ? ?

No, ako elementi skupa čine neku pravilnu konfiguraciju, a pritom ih ne moramo direktno odrediti nego samo prebrojiti, onda broj elemenata toga skupa možemo odrediti služeći se nekom od metoda prebrojavanja. Kombinatorika upravo pronalazi i istražuje te metode.

Razlikujemo prebrojavanja: tri osnovne metode ili pravila pravilo jednakosti, pravilo zbroja, pravilo produkta, ovisno o tome znamo li direktno odrediti broj elemenata nekog skupa, njegove dijelove ili njegove faktore.

1. Pravilo jednakosti Neka su S i T konačni skupovi. Tada je |S|=|T| ako i samo ako postoji bijekcija među skupovima S i T.

2. Pravilo zbroja Neka je , te neka su međusobno disjunktni skupovi. Tada je skup i konačni konačan

3. Pravilo umnoška Neka je skupovi. , te neka su Tada je Kartezijev produkt konačan skup i konačni

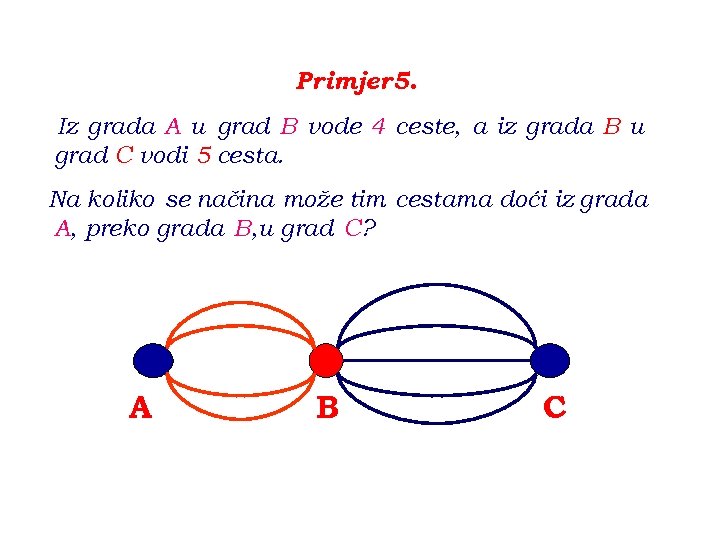Primjer 5. Iz grada A u grad B vode 4 ceste, a iz grada B u grad C vodi 5 cesta. Na koliko se načina može tim cestama doći iz grada A, preko grada B, u grad C? A B C

Svatko se od nas susreo s bar nekim kombinatornim problemom. Npr. • Na koliko se načina može izvući 7 brojeva od mogućih 49 u igri LOTO?

Na koliko načina možemo zadati šifru koja se sastoji od tri znamenke, a otvara bravu na torbi?

Ili mnogo složeniju šifru koja otvara sef?

Koliko se automobila može registrirati u nekom gradu ako se registracijska tablica sastoji od tri broja i dva slova? . . .

Kombinacije, varijacije, permutacije

Primjer 6. Na jednoj proslavi sretnu se 4 prijatelja i svi se međusobno rukuju točno jednom. Koliko je bilo rukovanja?

Da su bila 2 prijatelja bilo bi 1 rukovanje. Da su 3 prijatelja, prvi bi se rukovati s drugim i trećim, te još drugi s trećim, pa imamo 2+1=3 rukovanja. Za četvoricu prijatelja imamo 3+2+1=6 rukovanja.

Povećavanjem broja prijatelja naglo se povećava i broj rukovanja, pa brojanje postaje sve složenije. Stoga bi se lako moglo dogoditi da se preskoči neko rukovanje i tako ne uzmu u obzir sve mogućnosti.

Ali možemo se pomoći nečim drugim. Naime, možemo uočiti izvjesne pravilnosti i zakonitosti. Za 5 prijatelja, broj rukovanja je 1+2+3+4=10. Za 6 prijatelja, broj rukovanja je 1+2+3+4+5=15. . .

Lako se pokaže (indukcijom) da je za n prijatelja broj rukovanja jednak 1+2+. . . +(n-1)=n(n-1)/2. Dakle, iz uočene pravilnosti je proizašla opća formula po kojoj se mogu riješiti svi zadatci tog tipa.

Generalizirajmo: Ako prijatelje označimo s 1, 2, . . . , n, onda naš problem glasi: Kolikoima različitih dvojki i j pri čemu poredaknije bitan jer jei j i isto rukovanje (rukovanje istih ljudi). To je stoga ekvivalentno problemu: Koliko ima svih dvočlanih podskupova skup od n elemenata?

Općenito, r-kombinacijan-članog skupa S je svaki rčlani podskup od S. Broj svih r-kombinacijaiznosi Dakle, kad god iz nekog skupa koji ima n elemenata odabiremo r različitih, a da nam pritom njihov poredak nije važan, broj načina da to učinimo jednak je broju svih r-kombinacija n-članog skupa.

ZADATCI a) Na koliko je načina moguće formirati tročlanu delegaciju iz društva od 70 ljudi? b) Kolika je vjerojatnost da će točno određena dva prijatelja biti u toj delegaciji?

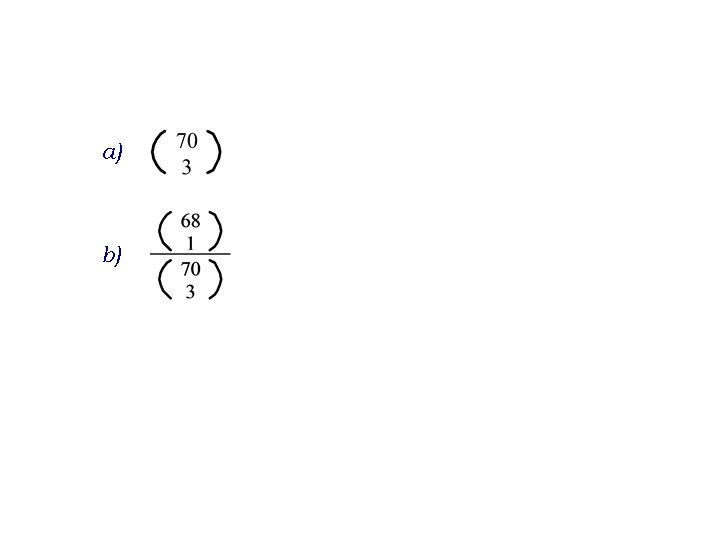a) b)

U nekom hotelu je 176 gostiju. Gazda je odlučio 11 gostiju počastiti bocom dobrog vina. a) Na koliko načina može odabrati te goste? b) b) Kolika je vjerojatnost da jedan točno određeni gost bude počaščen?

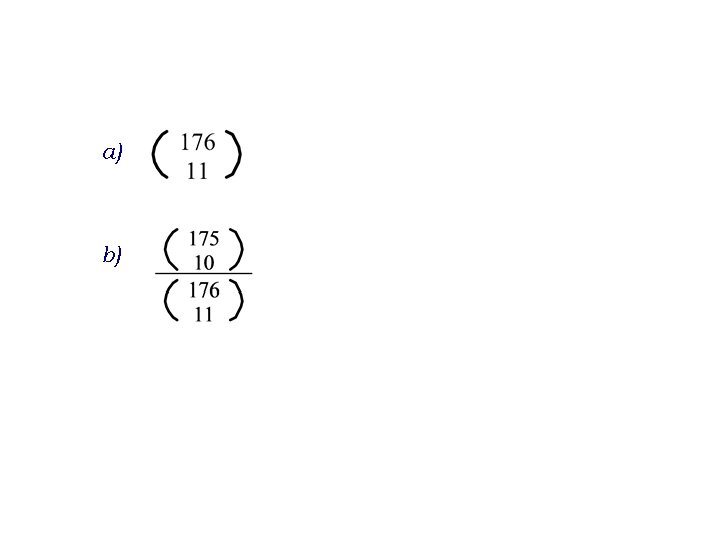a) b)

a) Na koliko se načina može izvući 7 brojeva od mogućih 49 u igri LOTO? b) Kolika je vjerojatnost da dobijemo sedmicu ako smo uplatili samo jedan listić?

a) b)

Vratimo se našim prijateljima. Nakon ugodne večeri zaključili su da se trebaju češće družiti. Dogovorili su se da svaki prijatelj zasebno dođe u kućni posjet svakom od preostalih prijatelja. Koliko su posjeta dogovorili?

Označimo prijatelje s 1, 2, 3 i 4. Sada naš problem glasi: Koliko ima različitihdvojki i j pri čemu je poredak bitan jer su i j i posjeti u različitimkućama, tj. različiti posjeti. To je stoga ekvivalentno problemu: Koliko se uređenih parova može načinitiod različitih elemenata četveročlanog skupa?

Općenito, r-varijacija r-permutacija ili n-članog skupa S je svaka uređena r-torka međusobno različitih elemenata iz S. Broj svih r-varijacija iznosi Dakle, kad god iz nekog skupa koji ima n elemenata treba odabrati r različitih, a da nam je pritom poredak važan, radi se o r-varijaciji n-članog skupa.

U našem slučaju je n=4, r=2, pa je ukupno 4*3=12 posjeta. dogovoreno

a) Na koliko je načina moguće odabrati predsjednika, potpredsjednika i tajnika društva koje ima 70 članova, od kojih je 30 žena, ako jedna osoba smije obnašati samo jednu funkciju? b) Kolika je vjerojatnost da sve tri odabrane osobe budu žene?

a) b)

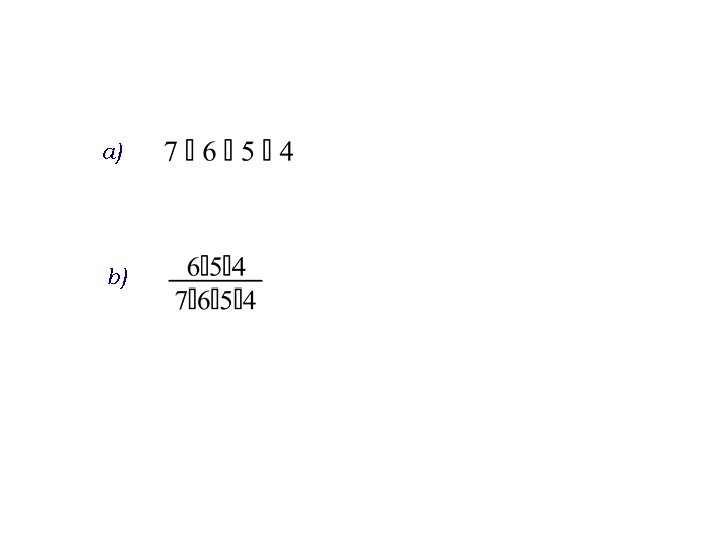
Ispod bora je 7 darova, a na jednom daru piše ime djeteta kojem je namjenjeno. Dolazi četvero djece i svako dijete nasumce uzima točno 1 dar. a) Na koliko načina djeca mogu uzeti darove? b) Kolika je vjerojatnost da je dijete kojem je dar bio namjenjen dobilo svoj dar?

a) b)

Ako dopustimo ponavljanje elemenata, onda je broj razmještaja veći. Radi se tada o varijacijama s ponavljanjem. Broj svih r-varijacijas ponavljanjemn-članog skupa je

Koliko ima peteroznamenkastih brojeva ako a) nije dopušteno da se znamenke ponavljaju? b) je dopušteno da se znamnke ponavljaju?

a) 9× 9× 8 × 7× 6 b) 9 × 10× 10

Svaka n-varijacija n-članog skupa naziva se permutacija(lat. permutare= promijeniti) tog skupa. Broj svih permutacija je

Sedam prijatelja kupilo je 7 karata za kino. Na koliko ih načina oni mogu međusobno podijeliti?

7 6 Rj. 7! 5 4 3 2 1

Kada bismo htjeli 10 knjiga ispremještati na polici na sve moguće načine, vidjeli bismo da je to golem posao jer se tih 10 knjiga može poredati, ni manje ni više, nego na 10!=3 628 800 različitih načina.

No, kada bi neke od tih knjiga bile iste, razmještaja bi bilo znatno manje. Npr. ako od tih 10 knjiga imamo samo tri različite i to: 2 × K 1, 3 × K 2 i 5 × K 3, tada se ukupni broj svih razmještaja treba podijeliti s brojem razmještaja istih knjiga (jer razmještaji istih knjiga su isti razmještaji). Broj razmještaja je stoga: Takve razmještaje ponavljanjem. nazivamo permutacije s

Npr. koliko se desetslovnih riječi može načiniti od riječi MATEMATIKA ? A koliko se devetslovnih riječi može načiniti od riječi DUBROVNIK ? 9! = 62880.

Prijatelji na rastanku

Bilo je već prilično kasno kada su se naši prijatelji odlučili rastati. Kako se na svakoj zabavi obično obilno popije, ustali su teturajući i krenuli da s vješalica uzmu svoje šešire. Pokazalo se da je svaki od njih uzeo pogrešan šešir. Na koliko su načina mogli to učiniti ?

Idemo postepeno. Ako su dvojica označimo ih sa A i B, a njihove šešire , sa a i b, onda može biti samo ovaj slučaj: A b, Ba. Ako su trojica. A, B, C, onda su dva slučaja: A b Bc Ca A c Ba Cb. Kako bi bilo za njih četvoricu: A, B, C i D?

Ako je A uzeo šešir b, imamo sljedeće tri mogućnosti : A b Ba Cd Dc A b Bc Cd Da A b Bd Ca Dc. Ako je A otišao sa šeširom c, opet imamo tri mogućnosti. I napokon, da je A otišao sa šeširom d, bilo bi opet tri mogućnosti. Ukupno , dakle, ima 3× 3=9 mogućnosti.

Ovaj problem se popularno zove problem deranžmana ili totalnazbrka Već za n=5 imamo 44 mogućnosti i. ovako nabrajajući bio bi teško riješiv. Opće rješenje se dobije preko FUI-a: Ovaj problem su (drugom obliku) riješili L. Euler i N. Bernoulli. Radilo se o problemu “zamjene pisama”.

Odgovorimo još na De Mereovo pitanje koje je glasilo: Je li preporučljivo kladiti se da će u 24 uzastopna bacanja para različitih kocaka barem jednom pasti dvostruka šestica? A={u n bacanja pojavila se bar jednom dupla šestica}. c. A={u n bacanja nije se pojavila dvostruka šestica}, ═> Ako želimo izračunati koliko puta moramo baciti kocku da vjerojatnost da se dogodi događaj A bude barem 50%, onda treba vrijediti: Dakle, odgovor je: nije se preporučljivo kladiti.

Nadam se da je vjerojatnost da vam se svidjela ova prezentacija veća od 0. 5! Nadam se da je vjerojatnost da je nešto bilo nejasno gotovo 0. Sigurna sam da jevjerojatnost da je ovo kraj prezentacije jednaka 1!

Pri izradi korištena je sljedeća literatura: • Uvod u vjerojatnost i statistiku, predavanja i vježbe • Kombinatorika s teorijom grafova , D. Veljan, Školska knjiga, Zagreb • Kombinatorika, prezentacija Snježane Varge , profesorice matematike u srednjoj školi u Daruvaru • Uvod u vjerojatnostprezentacija Antonije Horvatek, , profesorice matematike u OŠ u Graberju Ivanićkom (http: //public. carnet. hr/~ahorvate/materijali. html)