Математика_Лекции_Презентация_Статистика.pptx
- Количество слайдов: 79
 Математика Лекции IV Раздел Основы статистики.
Математика Лекции IV Раздел Основы статистики.
 4. 1 Статистика. Основные понятия. Статистика — это наука, изучающая количественные изменения массовых общественных явлений и процессов в неразрывной связи с их качественным содержанием. ©Lyubimova. EM 03. 02. 2018 2
4. 1 Статистика. Основные понятия. Статистика — это наука, изучающая количественные изменения массовых общественных явлений и процессов в неразрывной связи с их качественным содержанием. ©Lyubimova. EM 03. 02. 2018 2
 4. 1 Статистика. Основные понятия. Для описания, оценки и анализа этих процессов и явлений применяют различные математические модели, в том числе и вероятностные. Эти модели строятся на следующих понятиях: O случайная величина; O математическое ожидание; O дисперсия; O законы распределения и др. ©Lyubimova. EM 03. 02. 2018 3
4. 1 Статистика. Основные понятия. Для описания, оценки и анализа этих процессов и явлений применяют различные математические модели, в том числе и вероятностные. Эти модели строятся на следующих понятиях: O случайная величина; O математическое ожидание; O дисперсия; O законы распределения и др. ©Lyubimova. EM 03. 02. 2018 3
 4. 1 Статистика. Основные понятия. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. ©Lyubimova. EM 03. 02. 2018 4
4. 1 Статистика. Основные понятия. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. ©Lyubimova. EM 03. 02. 2018 4
 4. 1 Статистика. Основные понятия. Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, . . . , 100. ©Lyubimova. EM 03. 02. 2018 5
4. 1 Статистика. Основные понятия. Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, . . . , 100. ©Lyubimova. EM 03. 02. 2018 5
 4. 1 Статистика. Основные понятия. Подобные случайные величины называются дискретными, т. к. они могут быть записаны в виде конечной или бесконечной последовательности значений. Кроме этого выделяют постоянную дискретную случайную величину, которая принимает одно и то же значение при любом испытании (аналог — достоверное и невозможные события). ©Lyubimova. EM 03. 02. 2018 6
4. 1 Статистика. Основные понятия. Подобные случайные величины называются дискретными, т. к. они могут быть записаны в виде конечной или бесконечной последовательности значений. Кроме этого выделяют постоянную дискретную случайную величину, которая принимает одно и то же значение при любом испытании (аналог — достоверное и невозможные события). ©Lyubimova. EM 03. 02. 2018 6
 4. 1 Статистика. Основные понятия. Если случайные величины принимают значения из некоторого числового промежутка (интервала), то они называются непрерывными (интервальными). ©Lyubimova. EM 03. 02. 2018 7
4. 1 Статистика. Основные понятия. Если случайные величины принимают значения из некоторого числового промежутка (интервала), то они называются непрерывными (интервальными). ©Lyubimova. EM 03. 02. 2018 7
 4. 1 Статистика. Основные понятия. Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д. ), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). ©Lyubimova. EM 03. 02. 2018 8
4. 1 Статистика. Основные понятия. Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д. ), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). ©Lyubimova. EM 03. 02. 2018 8
 4. 1 Статистика. Основные понятия. Генеральной (статистической) совокупностью называют множество однородных хотя бы по одному какомулибо признаку явлений, существование которых ограничено в пространстве и времени. Количество (N) входящих в генеральную совокупность объектов называют объемом генеральной совокупности. ©Lyubimova. EM 03. 02. 2018 9
4. 1 Статистика. Основные понятия. Генеральной (статистической) совокупностью называют множество однородных хотя бы по одному какомулибо признаку явлений, существование которых ограничено в пространстве и времени. Количество (N) входящих в генеральную совокупность объектов называют объемом генеральной совокупности. ©Lyubimova. EM 03. 02. 2018 9
 4. 1 Статистика. Основные понятия. Пример 3. При изучении квалификации работников предприятия элементом совокупности выступает конкретный работник, а границы совокупности ограничены рамками предприятия. ©Lyubimova. EM 03. 02. 2018 10
4. 1 Статистика. Основные понятия. Пример 3. При изучении квалификации работников предприятия элементом совокупности выступает конкретный работник, а границы совокупности ограничены рамками предприятия. ©Lyubimova. EM 03. 02. 2018 10
 4. 1 Статистика. Основные понятия. Пример 3. Генеральной совокупностью могут быть: O население района, города; O группа родившихся в данном году. O при изучении квалификации работников предприятия элементом совокупности выступает конкретный работник, а границы совокупности ограничены рамками предприятия. ©Lyubimova. EM 03. 02. 2018 11
4. 1 Статистика. Основные понятия. Пример 3. Генеральной совокупностью могут быть: O население района, города; O группа родившихся в данном году. O при изучении квалификации работников предприятия элементом совокупности выступает конкретный работник, а границы совокупности ограничены рамками предприятия. ©Lyubimova. EM 03. 02. 2018 11
 4. 1 Статистика. Основные понятия. Выборка – множество случайно отобранных объектов (значений) из генеральной совокупности. Объемом выборки (n) называется число входящих в нее объектов. К выборке предъявляется требование, чтобы она адекватно представляла генеральную совокупность, т. е. была репрезентативной (представительной). ©Lyubimova. EM 03. 02. 2018 12
4. 1 Статистика. Основные понятия. Выборка – множество случайно отобранных объектов (значений) из генеральной совокупности. Объемом выборки (n) называется число входящих в нее объектов. К выборке предъявляется требование, чтобы она адекватно представляла генеральную совокупность, т. е. была репрезентативной (представительной). ©Lyubimova. EM 03. 02. 2018 12
 4. 1 Статистика. Основные понятия. Основной характеристикой, как генеральной совокупности, так и выборки является их однородность, т. е. наличие для всех единиц совокупности основного свойства, качества, типичности. ©Lyubimova. EM 03. 02. 2018 13
4. 1 Статистика. Основные понятия. Основной характеристикой, как генеральной совокупности, так и выборки является их однородность, т. е. наличие для всех единиц совокупности основного свойства, качества, типичности. ©Lyubimova. EM 03. 02. 2018 13
 4. 2 Закон распределения Для того чтобы задать (определить) дискретную случайную величину недостаточно перечислить все ее возможные значения, нужно указать вероятности этих значений. ©Lyubimova. EM 03. 02. 2018 14
4. 2 Закон распределения Для того чтобы задать (определить) дискретную случайную величину недостаточно перечислить все ее возможные значения, нужно указать вероятности этих значений. ©Lyubimova. EM 03. 02. 2018 14
 4. 2 Закон распределения Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически (в виде формулы) и графически. ©Lyubimova. EM 03. 02. 2018 15
4. 2 Закон распределения Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически (в виде формулы) и графически. ©Lyubimova. EM 03. 02. 2018 15
 4. 2 Закон распределения При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные упорядоченные значения, а вторая — их вероятности: Х х1 х2 х3 … хn Р p 1 p 2 p 3 … pn т. к. все возможные значения X образуют полную группу событий, то сумма их вероятностей будет равна 1 P=p 1+p 2+p 3+…. +pn=1 ©Lyubimova. EM 03. 02. 2018 16
4. 2 Закон распределения При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные упорядоченные значения, а вторая — их вероятности: Х х1 х2 х3 … хn Р p 1 p 2 p 3 … pn т. к. все возможные значения X образуют полную группу событий, то сумма их вероятностей будет равна 1 P=p 1+p 2+p 3+…. +pn=1 ©Lyubimova. EM 03. 02. 2018 16
 4. 2 Закон распределения При графическом изображении закона распределения в декартовой системе координат O по оси абсцисс откладываются все возможные упорядоченные значения Х, O по оси ординат — соответствующие вероятности. На пересечении значений и соответствующих им вероятностей троят точки Мn (хn; pn). ©Lyubimova. EM 03. 02. 2018 17
4. 2 Закон распределения При графическом изображении закона распределения в декартовой системе координат O по оси абсцисс откладываются все возможные упорядоченные значения Х, O по оси ординат — соответствующие вероятности. На пересечении значений и соответствующих им вероятностей троят точки Мn (хn; pn). ©Lyubimova. EM 03. 02. 2018 17
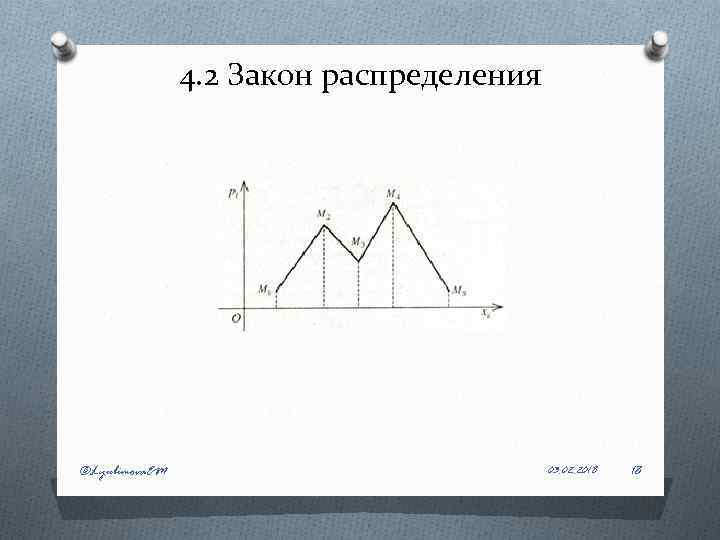 4. 2 Закон распределения ©Lyubimova. EM 03. 02. 2018 18
4. 2 Закон распределения ©Lyubimova. EM 03. 02. 2018 18
 4. 2 Закон распределения Пример 4. Найти ряд распределения случайной величины X — числа выпавших очков при однократном бросании игрального кубика. Х Р ©Lyubimova. EM 1 1/6 2 1/6 3 1/6 4 1/6 5 1/6 6 1/6 03. 02. 2018 19
4. 2 Закон распределения Пример 4. Найти ряд распределения случайной величины X — числа выпавших очков при однократном бросании игрального кубика. Х Р ©Lyubimova. EM 1 1/6 2 1/6 3 1/6 4 1/6 5 1/6 6 1/6 03. 02. 2018 19
 4. 2 Закон распределения Подобное распределение называется равномерным и графически представляет собой прямую, параллельную оси абсцисс. Р Х ©Lyubimova. EM 03. 02. 2018 20
4. 2 Закон распределения Подобное распределение называется равномерным и графически представляет собой прямую, параллельную оси абсцисс. Р Х ©Lyubimova. EM 03. 02. 2018 20
 4. 2 Закон распределения Пример 5. В денежной лотерее выпущено 1000 билетов. Разыгрывается 1 выигрыш в 10000 рублей, 10 выигрышей по 1000 рублей и 100 выигрышей по 100 рублей. Найти ряд распределения случайной величины Х — стоимость выигрыша для владельца одного лотерейного билета. ©Lyubimova. EM 03. 02. 2018 21
4. 2 Закон распределения Пример 5. В денежной лотерее выпущено 1000 билетов. Разыгрывается 1 выигрыш в 10000 рублей, 10 выигрышей по 1000 рублей и 100 выигрышей по 100 рублей. Найти ряд распределения случайной величины Х — стоимость выигрыша для владельца одного лотерейного билета. ©Lyubimova. EM 03. 02. 2018 21
 4. 2 Закон распределения Найдем вероятности соответствующих выигрышей: p 1=1/1000=0, 001; p 2=10/1000=0, 01; p 3=100/1000=0, 1; ©Lyubimova. EM 03. 02. 2018 22
4. 2 Закон распределения Найдем вероятности соответствующих выигрышей: p 1=1/1000=0, 001; p 2=10/1000=0, 01; p 3=100/1000=0, 1; ©Lyubimova. EM 03. 02. 2018 22
 4. 2 Закон распределения т. к. все возможные значения Х образуют полную группу событий, то p 1+p 2+p 3+p 4=1 p 4= 1 - (p 1+p 2+p 3) = 1 - 0, 111 = 0, 889. ©Lyubimova. EM 03. 02. 2018 23
4. 2 Закон распределения т. к. все возможные значения Х образуют полную группу событий, то p 1+p 2+p 3+p 4=1 p 4= 1 - (p 1+p 2+p 3) = 1 - 0, 111 = 0, 889. ©Lyubimova. EM 03. 02. 2018 23
 4. 2 Закон распределения Воспользуемся табличным заданием закона распределения дискретной случайной величины: Х Р ©Lyubimova. EM 100 Х 100 0, 001 Р 0, 001 10 10 0, 01 1 1 0 0, 1 0, 889 0, 1 0 0, 889 03. 02. 2018 24
4. 2 Закон распределения Воспользуемся табличным заданием закона распределения дискретной случайной величины: Х Р ©Lyubimova. EM 100 Х 100 0, 001 Р 0, 001 10 10 0, 01 1 1 0 0, 1 0, 889 0, 1 0 0, 889 03. 02. 2018 24
 4. 2 Закон распределения Подобное распределение называется монотонно убывающим. Упорядочим значения Х по возрастанию на оси абсцисс, тогда на графике закон распределения будет представлять собой нисходящую кривую. ©Lyubimova. EM 03. 02. 2018 25
4. 2 Закон распределения Подобное распределение называется монотонно убывающим. Упорядочим значения Х по возрастанию на оси абсцисс, тогда на графике закон распределения будет представлять собой нисходящую кривую. ©Lyubimova. EM 03. 02. 2018 25
 4. 2 Закон распределения Пример 6. Монета брошена 2 раза. Найти закон распределения случайной величины X — числа выпадений «герба» . Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q=1/2. ©Lyubimova. EM 03. 02. 2018 26
4. 2 Закон распределения Пример 6. Монета брошена 2 раза. Найти закон распределения случайной величины X — числа выпадений «герба» . Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q=1/2. ©Lyubimova. EM 03. 02. 2018 26
 4. 2 Закон распределения При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: Х Р ©Lyubimova. EM 2 p 2 1 p 3 0 p 4 03. 02. 2018 27
4. 2 Закон распределения При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: Х Р ©Lyubimova. EM 2 p 2 1 p 3 0 p 4 03. 02. 2018 27
 4. 2 Закон распределения Найдем вероятности этих значений (сложных событий) по формуле Бернулли. Рn(k) = Сkn * pkqn-k Вероятность сложного события – орел выпадет дважды: Р 2(2)=С 22*р2*q 0=1/22=0, 25 Вероятность сложного события – орел выпадет один раз: Р 1(1)=С 12*р1*q 1=2*1/21=0, 5 Вероятность сложного события – орел не выпадет дважды: Р 2(0)=С 02*р0*q 2=1/22=0, 25 ©Lyubimova. EM 03. 02. 2018 28
4. 2 Закон распределения Найдем вероятности этих значений (сложных событий) по формуле Бернулли. Рn(k) = Сkn * pkqn-k Вероятность сложного события – орел выпадет дважды: Р 2(2)=С 22*р2*q 0=1/22=0, 25 Вероятность сложного события – орел выпадет один раз: Р 1(1)=С 12*р1*q 1=2*1/21=0, 5 Вероятность сложного события – орел не выпадет дважды: Р 2(0)=С 02*р0*q 2=1/22=0, 25 ©Lyubimova. EM 03. 02. 2018 28
 4. 2 Закон распределения Подобное распределение называется биномиальным, т. к. в основе определения вероятностей лежит формула бинома Ньютона. ©Lyubimova. EM 03. 02. 2018 29
4. 2 Закон распределения Подобное распределение называется биномиальным, т. к. в основе определения вероятностей лежит формула бинома Ньютона. ©Lyubimova. EM 03. 02. 2018 29
 4. 2 Закон распределения Также в статистике используются и другие законы распределения, например, нормальное распределение. Но его определение требует ввода некоторых других математических и статистических понятий. ©Lyubimova. EM 03. 02. 2018 30
4. 2 Закон распределения Также в статистике используются и другие законы распределения, например, нормальное распределение. Но его определение требует ввода некоторых других математических и статистических понятий. ©Lyubimova. EM 03. 02. 2018 30
 4. 3 Характеристики случайной величины и статистические показатели В некоторых случаях, например, когда не известен закон распределения, для анализа случайной величины используют так называемые «суммарные» (интегральные) свойства случайной величины, которые в статистике называются статистическими показателями. Рассмотрим некоторые из них. ©Lyubimova. EM 03. 02. 2018 31
4. 3 Характеристики случайной величины и статистические показатели В некоторых случаях, например, когда не известен закон распределения, для анализа случайной величины используют так называемые «суммарные» (интегральные) свойства случайной величины, которые в статистике называются статистическими показателями. Рассмотрим некоторые из них. ©Lyubimova. EM 03. 02. 2018 31
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Оно показывает, вокруг какой точки группируются значения случайной величины, являясь одним из показателей центра распределения. М(Х) = х1*р1 + х2*р2 + х3*р3 + … + хn*рn ©Lyubimova. EM 03. 02. 2018 32
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Оно показывает, вокруг какой точки группируются значения случайной величины, являясь одним из показателей центра распределения. М(Х) = х1*р1 + х2*р2 + х3*р3 + … + хn*рn ©Lyubimova. EM 03. 02. 2018 32
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Пример 7. Найти математическое ожидание дискретной случайной величины, если известен ряд ее распределения: Х 3 5 2 Р 0, 1 0, 6 0, 3 М(Х) = 3*0, 1 + 5*0, 6 + 2*0, 3 = 3, 9 ©Lyubimova. EM 03. 02. 2018 33
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Пример 7. Найти математическое ожидание дискретной случайной величины, если известен ряд ее распределения: Х 3 5 2 Р 0, 1 0, 6 0, 3 М(Х) = 3*0, 1 + 5*0, 6 + 2*0, 3 = 3, 9 ©Lyubimova. EM 03. 02. 2018 33
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Пример 8. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность наступления события А = р. Случайная величина Х может принимать только два значения: 1 с вероятностью р – событие А произошло или 0 с вероятностью q – событие А не произошло. ©Lyubimova. EM 03. 02. 2018 34
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Пример 8. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность наступления события А = р. Случайная величина Х может принимать только два значения: 1 с вероятностью р – событие А произошло или 0 с вероятностью q – событие А не произошло. ©Lyubimova. EM 03. 02. 2018 34
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Следовательно, ряд распределения будет выглядеть следующим образом: Х 1 0 Р p q Тогда М(Х) = 1*p + 0*q = p. ©Lyubimova. EM 03. 02. 2018 35
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Следовательно, ряд распределения будет выглядеть следующим образом: Х 1 0 Р p q Тогда М(Х) = 1*p + 0*q = p. ©Lyubimova. EM 03. 02. 2018 35
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Пример 9. Найти математическое ожидание случайной величины Х — числа выпавших очков при однократном бросании игральной кости. М(Х) = 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6= =21/6 = 3, 5. ©Lyubimova. EM 03. 02. 2018 36
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Пример 9. Найти математическое ожидание случайной величины Х — числа выпавших очков при однократном бросании игральной кости. М(Х) = 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6= =21/6 = 3, 5. ©Lyubimova. EM 03. 02. 2018 36
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Средняя арифметическая величина – это статистическая характеристика, которая отражает только типичные проявления признака в исследуемой совокупности. Она может быть представлена в двух формах: взвешенной и невзвешенной. ©Lyubimova. EM 03. 02. 2018 37
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Средняя арифметическая величина – это статистическая характеристика, которая отражает только типичные проявления признака в исследуемой совокупности. Она может быть представлена в двух формах: взвешенной и невзвешенной. ©Lyubimova. EM 03. 02. 2018 37
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Невзвешенная форма используется, если исходные данные представлены в несгруппированном виде. Студенты Таня Оценки (х) 4 ©Lyubimova. EM Петя Вася Лена Гена Вера Лера Гера Надя Ваня 3 5 4 3 4 4 2 03. 02. 2018 38
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Невзвешенная форма используется, если исходные данные представлены в несгруппированном виде. Студенты Таня Оценки (х) 4 ©Lyubimova. EM Петя Вася Лена Гена Вера Лера Гера Надя Ваня 3 5 4 3 4 4 2 03. 02. 2018 38
 4. 3. 1 Показатели центра распределения: O математическое ожидание и средняя арифметическая величина ©Lyubimova. EM 03. 02. 2018 39
4. 3. 1 Показатели центра распределения: O математическое ожидание и средняя арифметическая величина ©Lyubimova. EM 03. 02. 2018 39
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Эта же таблица может быть представлена сгуппированными данными. Тогда значения, которые принимает Х (пятибалльная система оценивания) будут записаны в первой строке таблицы, а количество студентов, которые эти оценки получили — во второй. ©Lyubimova. EM 03. 02. 2018 40
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Эта же таблица может быть представлена сгуппированными данными. Тогда значения, которые принимает Х (пятибалльная система оценивания) будут записаны в первой строке таблицы, а количество студентов, которые эти оценки получили — во второй. ©Lyubimova. EM 03. 02. 2018 40
 4. 3. 1 Показатели центра распределения: O математическое ожидание и средняя арифметическая величина Х Кол-во студентов ©Lyubimova. EM 1 0 2 1 3 3 4 4 5 2 Итого 10 студентов 03. 02. 2018 41
4. 3. 1 Показатели центра распределения: O математическое ожидание и средняя арифметическая величина Х Кол-во студентов ©Lyubimova. EM 1 0 2 1 3 3 4 4 5 2 Итого 10 студентов 03. 02. 2018 41
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Х Кол-во студентов 1 0 2 1 3 3 4 4 5 2 Итого 10 студентов где mi – количество студентов, обладающих какойлибо оценкой. Тогда, (1*0+2*1+3*3+4*4+5*2) /10 = 3, 7. ©Lyubimova. EM 03. 02. 2018 42
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Х Кол-во студентов 1 0 2 1 3 3 4 4 5 2 Итого 10 студентов где mi – количество студентов, обладающих какойлибо оценкой. Тогда, (1*0+2*1+3*3+4*4+5*2) /10 = 3, 7. ©Lyubimova. EM 03. 02. 2018 42
 4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Математическое ожидание имеет вероятностный характер. Это отражается в законе больших чисел. Эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. ©Lyubimova. EM 03. 02. 2018 43
4. 3. 1 Показатели центра распределения: математическое ожидание и средняя арифметическая величина Математическое ожидание имеет вероятностный характер. Это отражается в законе больших чисел. Эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. ©Lyubimova. EM 03. 02. 2018 43
 4. 3. 2 Мода и медиана Помимо средней арифметической к показателям центра распределения относятся также мода и медиана. Мода распределения (Мо) — это такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т. е. один из вариантов признака повторяется чаще, чем все другие. Мода отражает типичный, наиболее распространенный вариант значения признака. ©Lyubimova. EM 03. 02. 2018 44
4. 3. 2 Мода и медиана Помимо средней арифметической к показателям центра распределения относятся также мода и медиана. Мода распределения (Мо) — это такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т. е. один из вариантов признака повторяется чаще, чем все другие. Мода отражает типичный, наиболее распространенный вариант значения признака. ©Lyubimova. EM 03. 02. 2018 44
 4. 3. 2 Мода и медиана Пример 10. По несгруппированным данным: 11 человек имеют следующие тарифные разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5. Тарифный разряд 5 будет модальным. ©Lyubimova. EM 03. 02. 2018 45
4. 3. 2 Мода и медиана Пример 10. По несгруппированным данным: 11 человек имеют следующие тарифные разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5. Тарифный разряд 5 будет модальным. ©Lyubimova. EM 03. 02. 2018 45
 4. 3. 2 Мода и медиана Для упорядоченного дискретного ряда распределения мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариантов и соответствует варианту с наибольшей частотой. ©Lyubimova. EM 03. 02. 2018 46
4. 3. 2 Мода и медиана Для упорядоченного дискретного ряда распределения мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариантов и соответствует варианту с наибольшей частотой. ©Lyubimova. EM 03. 02. 2018 46
 4. 3. 2 Мода и медиана Группы рабочих по тарифному разряду, х Численность рабочих, чел. Накопленные частоты, s A 1 2 2 3 4 5 6 20 50 60 70 15 20 70 130 Итого ©Lyubimova. EM 215 03. 02. 2018 47
4. 3. 2 Мода и медиана Группы рабочих по тарифному разряду, х Численность рабочих, чел. Накопленные частоты, s A 1 2 2 3 4 5 6 20 50 60 70 15 20 70 130 Итого ©Lyubimova. EM 215 03. 02. 2018 47
 4. 3. 2 Мода и медиана Медиана (Ме) — это величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, сумма отклонений значений признака от медианы меньше, чем от любой другой величины. Медиана выполняет функцию средней величины для неоднородной совокупности, не подчиняющейся нормальному закону распределения. ©Lyubimova. EM 03. 02. 2018 48
4. 3. 2 Мода и медиана Медиана (Ме) — это величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, сумма отклонений значений признака от медианы меньше, чем от любой другой величины. Медиана выполняет функцию средней величины для неоднородной совокупности, не подчиняющейся нормальному закону распределения. ©Lyubimova. EM 03. 02. 2018 48
 4. 3. 2 Мода и медиана Распределения, где средняя арифметическая не дает объективной характеристики большинства из группы исследуемых характеризуется показателями медиана. № п/п 1 2 3 4 … 50 51 … 99 100 Доход, долл. 100 104 107 … 162 164 … 200 50000 ©Lyubimova. EM 03. 02. 2018 49
4. 3. 2 Мода и медиана Распределения, где средняя арифметическая не дает объективной характеристики большинства из группы исследуемых характеризуется показателями медиана. № п/п 1 2 3 4 … 50 51 … 99 100 Доход, долл. 100 104 107 … 162 164 … 200 50000 ©Lyubimova. EM 03. 02. 2018 49
 4. 3. 2 Мода и медиана Пример 11. Определение медианы при нечетном числе вариантов. 11 человек имеют следующие тарифные разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5. Для определения медианы следует провести ранжирование рабочих по тарифному разряду: 2, 3, 3, 4, 4, 5, 5, 6, 6. ©Lyubimova. EM 03. 02. 2018 50
4. 3. 2 Мода и медиана Пример 11. Определение медианы при нечетном числе вариантов. 11 человек имеют следующие тарифные разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5. Для определения медианы следует провести ранжирование рабочих по тарифному разряду: 2, 3, 3, 4, 4, 5, 5, 6, 6. ©Lyubimova. EM 03. 02. 2018 50
 4. 3. 2 Мода и медиана Пример 11. Определение медианы при четном числе вариантов. Если ранжированный ряд включает 12 рабочих: 2, 3, 3, 3, 4, 4, 5, 5, 6, 6; то находится средняя арифметическая двух центральных значений разряда: (4+5/2)=4, 5. ©Lyubimova. EM 03. 02. 2018 51
4. 3. 2 Мода и медиана Пример 11. Определение медианы при четном числе вариантов. Если ранжированный ряд включает 12 рабочих: 2, 3, 3, 3, 4, 4, 5, 5, 6, 6; то находится средняя арифметическая двух центральных значений разряда: (4+5/2)=4, 5. ©Lyubimova. EM 03. 02. 2018 51
 4. 3. 3 Показатели степени вариации Показатели центра распределения не всегда дают полную характеристику вариационному ряду. Для более глубокого анализа распределения случайной величины используют показатели размаха вариации, дисперсии и среднего квадратического отклонения (стандартного отклонения). ©Lyubimova. EM 03. 02. 2018 52
4. 3. 3 Показатели степени вариации Показатели центра распределения не всегда дают полную характеристику вариационному ряду. Для более глубокого анализа распределения случайной величины используют показатели размаха вариации, дисперсии и среднего квадратического отклонения (стандартного отклонения). ©Lyubimova. EM 03. 02. 2018 52
 4. 3. 3 Показатели степени вариации Размах вариации (R) – показатель, определяющий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака. Зависимость для его расчета имеет вид: R= хmax – хmin. ©Lyubimova. EM 03. 02. 2018 53
4. 3. 3 Показатели степени вариации Размах вариации (R) – показатель, определяющий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака. Зависимость для его расчета имеет вид: R= хmax – хmin. ©Lyubimova. EM 03. 02. 2018 53
 4. 3. 3 Показатели степени вариации Пример 12. Найти дисперсию случайной величины Х, которая задана следующим законом распределения: X 1 2 5 p 0, 3 0, 5 0, 2 Решение: Найдем математическое ожидание: M(X)=1*0, 3+2*0, 5+5*0, 2=2, 3. ©Lyubimova. EM 03. 02. 2018 54
4. 3. 3 Показатели степени вариации Пример 12. Найти дисперсию случайной величины Х, которая задана следующим законом распределения: X 1 2 5 p 0, 3 0, 5 0, 2 Решение: Найдем математическое ожидание: M(X)=1*0, 3+2*0, 5+5*0, 2=2, 3. ©Lyubimova. EM 03. 02. 2018 54
 4. 3. 3 Показатели степени вариации Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида Х р 50 0, 8 Y p ©Lyubimova. EM 49 0, 1 0 0, 5 51 0, 1 100 0, 5 03. 02. 2018 55
4. 3. 3 Показатели степени вариации Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида Х р 50 0, 8 Y p ©Lyubimova. EM 49 0, 1 0 0, 5 51 0, 1 100 0, 5 03. 02. 2018 55
 4. 3. 3 Показатели степени вариации Х р Y p 49 0, 1 0 0, 5 50 0, 8 51 0, 1 100 0, 5 Найдем М(Х) = 49·0, 1 + 50·0, 8 + 51·0, 1 = 50, М(Y) = 0·0, 5 + 100·0, 5 = 50. Как видно, математические ожидания обеих величин равны, но если для Х М(Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М(Y). ©Lyubimova. EM 03. 02. 2018 56
4. 3. 3 Показатели степени вариации Х р Y p 49 0, 1 0 0, 5 50 0, 8 51 0, 1 100 0, 5 Найдем М(Х) = 49·0, 1 + 50·0, 8 + 51·0, 1 = 50, М(Y) = 0·0, 5 + 100·0, 5 = 50. Как видно, математические ожидания обеих величин равны, но если для Х М(Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М(Y). ©Lyubimova. EM 03. 02. 2018 56
 4. 3. 3 Показатели степени вариации Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия. Опр. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D(X) = M (X – M(X))². ©Lyubimova. EM 03. 02. 2018 57
4. 3. 3 Показатели степени вариации Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия. Опр. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D(X) = M (X – M(X))². ©Lyubimova. EM 03. 02. 2018 57
 4. 3. 3 Показатели степени вариации X 1 2 5 p 0, 3 0, 5 0, 2 Найдем все возможные значения квадрата отклонения: [x 1 -M(X)]2=(1 -2, 3)2=1, 69; [x 2 -M(X)]2=(2 -2, 3)2=0, 09; [x 3 -M(X)]2=(5 -2, 3)2=7, 29; Напишем закон распределения квадрата отклонения: [X-M(X)] 2 1, 69 0, 09 7, 29 p 0, 3 0, 5 0, 2 03. 02. 2018 ©Lyubimova. EM 58
4. 3. 3 Показатели степени вариации X 1 2 5 p 0, 3 0, 5 0, 2 Найдем все возможные значения квадрата отклонения: [x 1 -M(X)]2=(1 -2, 3)2=1, 69; [x 2 -M(X)]2=(2 -2, 3)2=0, 09; [x 3 -M(X)]2=(5 -2, 3)2=7, 29; Напишем закон распределения квадрата отклонения: [X-M(X)] 2 1, 69 0, 09 7, 29 p 0, 3 0, 5 0, 2 03. 02. 2018 ©Lyubimova. EM 58
![4. 3. 3 Показатели степени вариации [X-M(X)] 2 1, 69 0, 09 7, 29 4. 3. 3 Показатели степени вариации [X-M(X)] 2 1, 69 0, 09 7, 29](https://present5.com/presentation/1/80147739_241123091.pdf-img/80147739_241123091.pdf-59.jpg) 4. 3. 3 Показатели степени вариации [X-M(X)] 2 1, 69 0, 09 7, 29 p 0, 3 0, 5 0, 2 По определению, D(X)=1, 69*0, 3+0, 09*0, 5+7, 29*0, 2=2, 01 ©Lyubimova. EM 03. 02. 2018 59
4. 3. 3 Показатели степени вариации [X-M(X)] 2 1, 69 0, 09 7, 29 p 0, 3 0, 5 0, 2 По определению, D(X)=1, 69*0, 3+0, 09*0, 5+7, 29*0, 2=2, 01 ©Lyubimova. EM 03. 02. 2018 59
 4. 3. 3 Показатели степени вариации В статистике формулировка и запись формулы дисперсии (также как и формула математического ожидания) имеют несколько другой вид и используется в двух формах (взвешенной и невзвешенной). Дисперсия — средняя величина квадратов отклонений индивидуальных значений признака от их средней величины. ©Lyubimova. EM 03. 02. 2018 60
4. 3. 3 Показатели степени вариации В статистике формулировка и запись формулы дисперсии (также как и формула математического ожидания) имеют несколько другой вид и используется в двух формах (взвешенной и невзвешенной). Дисперсия — средняя величина квадратов отклонений индивидуальных значений признака от их средней величины. ©Lyubimova. EM 03. 02. 2018 60
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 61
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 61
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 62
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 62
 4. 3. 3 Показатели степени вариации Среднеквадратическое отклонение – корень квадратный из дисперсии. Часто используется в качестве единицы измерения отклонений от средней арифметической. ©Lyubimova. EM 03. 02. 2018 63
4. 3. 3 Показатели степени вариации Среднеквадратическое отклонение – корень квадратный из дисперсии. Часто используется в качестве единицы измерения отклонений от средней арифметической. ©Lyubimova. EM 03. 02. 2018 63
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 64
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 64
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 65
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 65
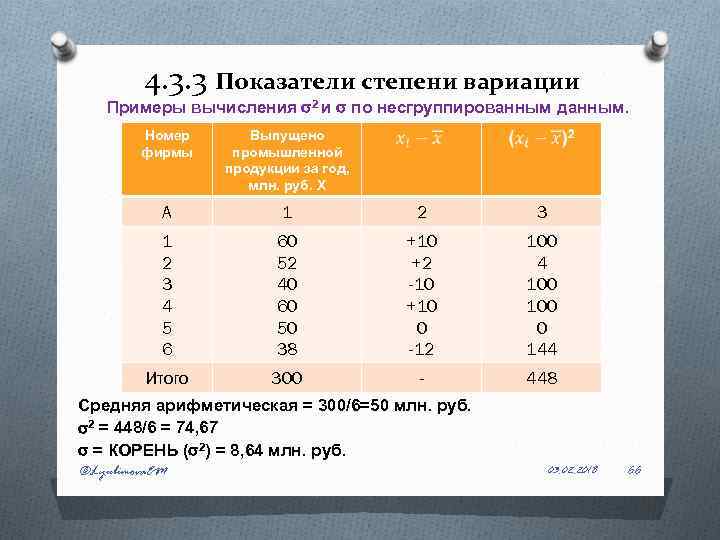 4. 3. 3 Показатели степени вариации Примеры вычисления 2 и по несгруппированным данным. Номер фирмы Выпущено промышленной продукции за год, млн. руб. Х A 1 2 3 4 5 6 60 52 40 60 50 38 +10 +2 -10 +10 0 -12 100 4 100 0 144 Итого 300 - 448 Средняя арифметическая = 300/6=50 млн. руб. 2 = 448/6 = 74, 67 = КОРЕНЬ ( 2) = 8, 64 млн. руб. ©Lyubimova. EM 03. 02. 2018 66
4. 3. 3 Показатели степени вариации Примеры вычисления 2 и по несгруппированным данным. Номер фирмы Выпущено промышленной продукции за год, млн. руб. Х A 1 2 3 4 5 6 60 52 40 60 50 38 +10 +2 -10 +10 0 -12 100 4 100 0 144 Итого 300 - 448 Средняя арифметическая = 300/6=50 млн. руб. 2 = 448/6 = 74, 67 = КОРЕНЬ ( 2) = 8, 64 млн. руб. ©Lyubimova. EM 03. 02. 2018 66
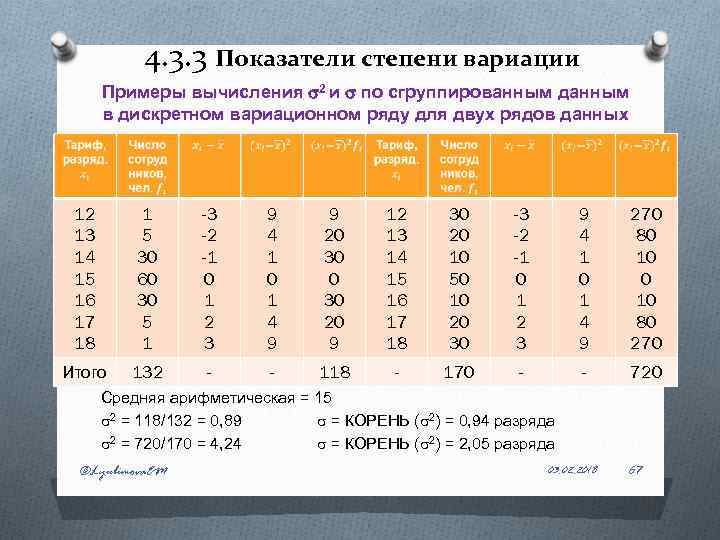 4. 3. 3 Показатели степени вариации Примеры вычисления 2 и по сгруппированным данным в дискретном вариационном ряду для двух рядов данных 12 13 14 15 16 17 18 1 5 30 60 30 5 1 -3 -2 -1 0 1 2 3 9 4 1 0 1 4 9 9 20 30 20 9 12 13 14 15 16 17 18 30 20 10 50 10 20 30 -3 -2 -1 0 1 2 3 9 4 1 0 1 4 9 270 80 10 80 270 Итого 132 - - 118 - 170 - - 720 Средняя арифметическая = 15 2 = 118/132 = 0, 89 = КОРЕНЬ ( 2) = 0, 94 разряда 2 = 720/170 = 4, 24 = КОРЕНЬ ( 2) = 2, 05 разряда ©Lyubimova. EM 03. 02. 2018 67
4. 3. 3 Показатели степени вариации Примеры вычисления 2 и по сгруппированным данным в дискретном вариационном ряду для двух рядов данных 12 13 14 15 16 17 18 1 5 30 60 30 5 1 -3 -2 -1 0 1 2 3 9 4 1 0 1 4 9 9 20 30 20 9 12 13 14 15 16 17 18 30 20 10 50 10 20 30 -3 -2 -1 0 1 2 3 9 4 1 0 1 4 9 270 80 10 80 270 Итого 132 - - 118 - 170 - - 720 Средняя арифметическая = 15 2 = 118/132 = 0, 89 = КОРЕНЬ ( 2) = 0, 94 разряда 2 = 720/170 = 4, 24 = КОРЕНЬ ( 2) = 2, 05 разряда ©Lyubimova. EM 03. 02. 2018 67
 4. 3. 3 Показатели степени вариации Относительные показатели вариации используются для сравнения колеблемости различных признаков в одной и той же совокупности, либо при сравнении колеблемости одного и того же признака в разных совокупностях. Базой структуры этих показателей является средняя арифметическая. ©Lyubimova. EM 03. 02. 2018 68
4. 3. 3 Показатели степени вариации Относительные показатели вариации используются для сравнения колеблемости различных признаков в одной и той же совокупности, либо при сравнении колеблемости одного и того же признака в разных совокупностях. Базой структуры этих показателей является средняя арифметическая. ©Lyubimova. EM 03. 02. 2018 68
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 69
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 69
 4. 3. 3 Показатели степени вариации К относительным показателям вариации относятся Коэффициент вариации ©Lyubimova. EM 03. 02. 2018 70
4. 3. 3 Показатели степени вариации К относительным показателям вариации относятся Коэффициент вариации ©Lyubimova. EM 03. 02. 2018 70
 4. 3. 3 Показатели степени вариации Последний показатель получил наибольшее распространение в практических расчетах. Совокупность считается однородной, если коэффициент вариации не превышает 33%. ©Lyubimova. EM 03. 02. 2018 71
4. 3. 3 Показатели степени вариации Последний показатель получил наибольшее распространение в практических расчетах. Совокупность считается однородной, если коэффициент вариации не превышает 33%. ©Lyubimova. EM 03. 02. 2018 71
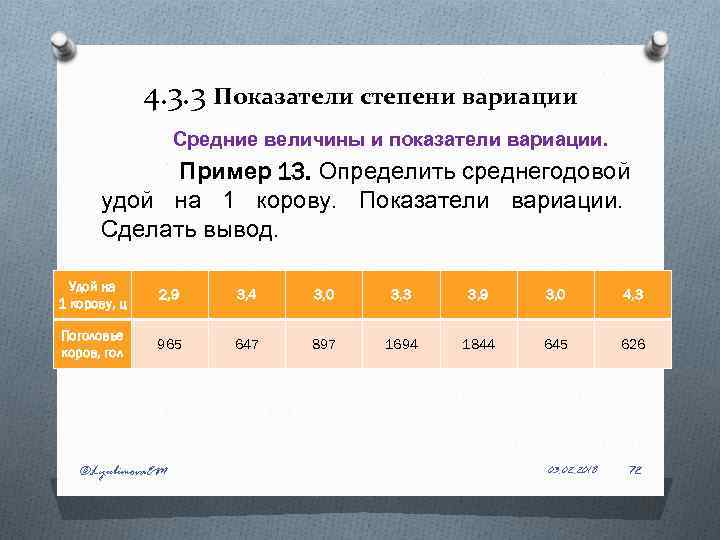 4. 3. 3 Показатели степени вариации Средние величины и показатели вариации. Пример 13. Определить среднегодовой удой на 1 корову. Показатели вариации. Сделать вывод. Удой на 1 корову, ц 2, 9 3, 4 3, 0 3, 3 3, 9 3, 0 4, 3 Поголовье коров, гол 965 647 897 1694 1844 645 626 ©Lyubimova. EM 03. 02. 2018 72
4. 3. 3 Показатели степени вариации Средние величины и показатели вариации. Пример 13. Определить среднегодовой удой на 1 корову. Показатели вариации. Сделать вывод. Удой на 1 корову, ц 2, 9 3, 4 3, 0 3, 3 3, 9 3, 0 4, 3 Поголовье коров, гол 965 647 897 1694 1844 645 626 ©Lyubimova. EM 03. 02. 2018 72
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 73
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 73
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 74
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 74
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 75
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 75
 4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 76
4. 3. 3 Показатели степени вариации O ©Lyubimova. EM 03. 02. 2018 76
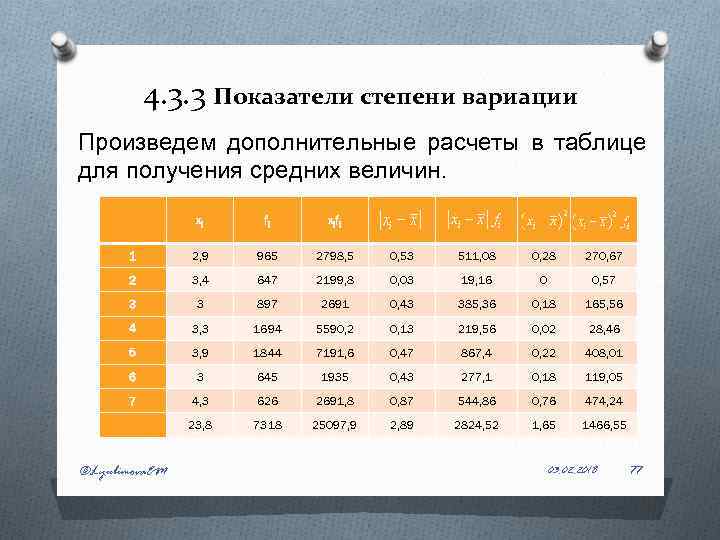 4. 3. 3 Показатели степени вариации Произведем дополнительные расчеты в таблице для получения средних величин. xi fi x i fi 1 2, 9 965 2798, 5 0, 53 511, 08 0, 28 270, 67 2 3, 4 647 2199, 8 0, 03 19, 16 0 0, 57 3 3 897 2691 0, 43 385, 36 0, 18 165, 56 4 3, 3 1694 5590, 2 0, 13 219, 56 0, 02 28, 46 5 3, 9 1844 7191, 6 0, 47 867, 4 0, 22 408, 01 6 3 645 1935 0, 43 277, 1 0, 18 119, 05 7 4, 3 626 2691, 8 0, 87 544, 86 0, 76 474, 24 23, 8 7318 25097, 9 2, 89 2824, 52 1, 65 1466, 55 ©Lyubimova. EM 03. 02. 2018 77
4. 3. 3 Показатели степени вариации Произведем дополнительные расчеты в таблице для получения средних величин. xi fi x i fi 1 2, 9 965 2798, 5 0, 53 511, 08 0, 28 270, 67 2 3, 4 647 2199, 8 0, 03 19, 16 0 0, 57 3 3 897 2691 0, 43 385, 36 0, 18 165, 56 4 3, 3 1694 5590, 2 0, 13 219, 56 0, 02 28, 46 5 3, 9 1844 7191, 6 0, 47 867, 4 0, 22 408, 01 6 3 645 1935 0, 43 277, 1 0, 18 119, 05 7 4, 3 626 2691, 8 0, 87 544, 86 0, 76 474, 24 23, 8 7318 25097, 9 2, 89 2824, 52 1, 65 1466, 55 ©Lyubimova. EM 03. 02. 2018 77
 4. 3. 3 Показатели степени вариации В результате получим следующие значения: ©Lyubimova. EM 03. 02. 2018 78
4. 3. 3 Показатели степени вариации В результате получим следующие значения: ©Lyubimova. EM 03. 02. 2018 78
 4. 3. 3 Показатели степени вариации Вычислим относительный Коэффициент вариации: показатель вариации. Вывод: среднегодовой удой на 1 корову составляет 3, 43 ц, со средним квадратическим отклонением 0, 45 ц. , т. е. в среднем удой коров отклонялся от среднего удоя на 0, 45 ц. Т. к. коэффициент вариации меньше 33%, т. е. данное поголовье коров достаточно однородно по удою. ©Lyubimova. EM 03. 02. 2018 79
4. 3. 3 Показатели степени вариации Вычислим относительный Коэффициент вариации: показатель вариации. Вывод: среднегодовой удой на 1 корову составляет 3, 43 ц, со средним квадратическим отклонением 0, 45 ц. , т. е. в среднем удой коров отклонялся от среднего удоя на 0, 45 ц. Т. к. коэффициент вариации меньше 33%, т. е. данное поголовье коров достаточно однородно по удою. ©Lyubimova. EM 03. 02. 2018 79


